† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant Nos. 2012CB821400, 2012CB921302, and 2015CB921303) and the National Natural Science Foundation of China (Grants Nos. 11274237, 91121004, 51228201, and 11004238). Wei Zhang also thanks the support of the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
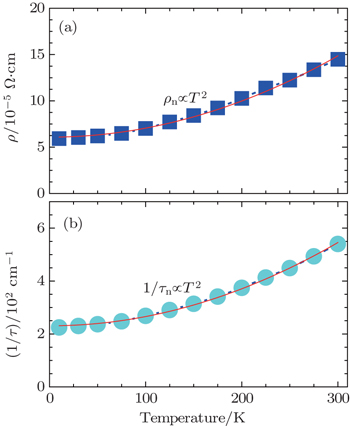
We present an infrared spectroscopy study of charge dynamics in CaCo2As2 single crystal. In this material, the optical conductivity can be described by two Drude components with different scattering rates (1/τ): a broad incoherent background and a narrow Drude component. By monitoring the temperature dependence, we find that only the narrow Drude component is temperature-dependent and determines the transport properties. Especially a Fermi liquid behavior of carriers is revealed by the T2 behavior in the dc resistivity ρn and scattering rate 1/τn, indicating a coherent nature of quasiparticles in the narrow Drude subsystem.
Chemical substitution, or doping, is the most common way to tune the properties of a correlated material. In iron-based superconductors (FeSCs), superconductivity is induced by various doping processes into metallic parent compounds. For example, in BaFe2As2 (122 system), doping with either electrons[1] or holes[2] suppresses the magnetic order, showing superconductivity with a maximum Tc close to the edges of the magnetic dome. The resistivity with different doping levels shows a temperature dependence from T linear to T2, revealing a crossover from non-Fermi liquid to Fermi liquid.[3–5]
FeSCs are Fe 3d6 multi-orbital systems. All the Fe 3d bands (or orbitals) exist near the Fermi level, resulting in complicated hole- and electron-like Fermi surface sheets,[6,7] and each Fe 3d band turns out to have different fillings and bandwidths.[8] In these multi-band systems the electronic correlations are mainly caused by the Hund rule coupling instead of the strong intraband Coulomb interactions as in cuprates.[9,10] Up to now, FeSCs were thought to be in the intermediate correlation regime. Nevertheless, many features, which are usually observed in some strongly correlated materials, were also found in FeSCs,[11,12] such as the linear temperature-dependent resistivity,[3,4] characteristic of a non-Fermi liquid. The non-Fermi-liquid behavior or linear temperature dependence of the resistivity is often taken as the hallmark of a quantum critical regime.[13,14]
It is well known that the electronic correlations in FeSCs are strongly band-dependent. The coexistence of electrons with different electronic correlations (coherent part and incoherent part) could be reflected in the charge excitation spectra which can be measured by the optical spectroscopy technique. In a multi-band environment, the optical conductivity is a sum of the contribution over the bands, and it happens to be parallel of resistances. Indeed, this is the case found by many previous optical studies on FeSCs,[15–19] in which the optical conductivity can be characterized by two Drude terms with different scattering rates; and the total Drude weight is a sum of terms ∼(n/m*)α, where n is a carrier concentration and m* is an effective mass, and α is the band index. Thus, in the situation of heavy differentiation of correlation strength, the transport properties are highly influenced by the bands of the weakly correlated ones (or more coherent ones).
Optical spectroscopy is a bulk-sensitive and energy-resolved probe, and it turns out to be a powerful tool to study charge dynamics of the multi-band system. In this paper, we report a detailed optical study on high quality CaCo2As2 single crystals, a counterpart of the 122 parent compound CaFe2As2. We found that the optical conductivity of CaCo2As2 can be decomposed into a narrow Drude (coherent) component and a broad incoherent background. Upon cooling, only the narrow Drude component is temperature-dependent and determines the transport properties. This subsystem reveals a T2 behavior in the dc resistivity and scattering rate disclosing a Fermi-liquid behavior in this material.
High-quality CaCo2As2 single crystals were grown with the flux method.[20] The ab-plane reflectivity R(ω) was measured at a near-normal angle of incidence on a Bruker VERTEX 80v FTIR spectrometer. An in situ gold overfilling technique[21] was used to obtain the absolute reflectivity R(ω) of the sample. Data from 50 to 15000 cm−1 were collected at 13 different temperatures from 300 K to 10 K on a freshly cleaved surface on an ARS–Helitran crysostat. Since a Kramers–Kronig analysis requires a broad spectral range, R(ω) was extended to the UV range (up to 50000 cm−1) at room temperature with an AvaSpec-2048×14 fiber optic spectrometer.
Figure
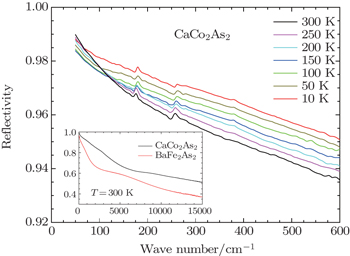 | Fig. 1. Temperature-dependent reflectivity of CaCo2As2 in the far infrared region. Inset: 300-K reflectivity over a wide frequency range for CaCo2As2 and BaFe2As2. |
The real part of the optical conductivity σ1(ω), which provides more direct information about the charge dynamics, has been determined via a Kramers–Kronig analysis of the reflectivity spectra R(ω).[27] Below the lowest measured frequency, we used a Hagen–Rubens form for the low-frequency extrapolation. Above the highest measured frequency, we assume a constant reflectivity up to 12.5 eV, followed by a free-electron (ω−4) response.
Figure
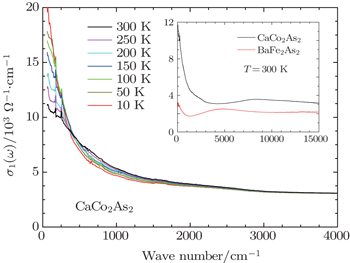 | Fig. 2. The real part of the optical conductivity at different temperatures for CaCo2As2 up to 4000 cm−1. Inset: 300-K optical conductivity over a wide frequency range for CaCo2As2 and BaFe2As2. |
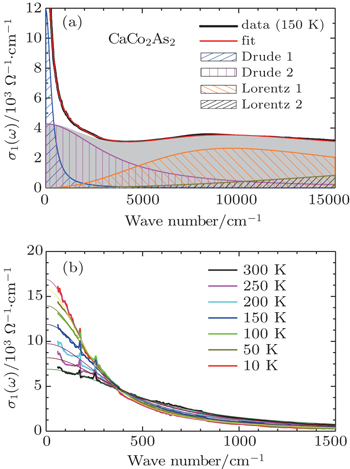
The optical conductivity is conveniently parameterized by a Drude–Lorentz model
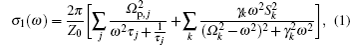
In the previous works on pnictides,[15–19] the optical conductivity σ1(ω) can be modeled reasonably by the superposition of two Drude components and series of Lorentz terms over a wide frequency range. As shown in Fig.
| Table 1. The Drude–Lorentz fitting results of the optical conductivity at 150 K, where Ωp,j and τj are the plasma frequency and scattering rate for the jth Drude component (Dj), and Ωk, Sk, and γ are the oscillator frequency, strength, and line width of the kth Lorentz mode (Lk). All units are in cm−1. . |
The temperature dependence of the two Drude components provides information about the nature of the two different types of carriers in this material. As shown in Fig.
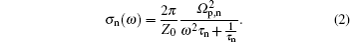
Upon cooling, the scattering rate 1/τn becomes narrowing, while the plasma frequency Ωp,n is roughly a constant, indicating that there seems to be no considerable transfer of spectral weight between both Drude subsystems. As shown in Table
The two Drude terms’ contributions to the total dc resistivity can be considered as a parallel circuit
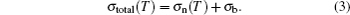
Figures
In summary, we have measured the electrodynamics properties of CaCo2As2 single crystal in a wide frequency range as a function of temperature. The optical conductivity of CaCo2As2 can be decomposed into a broad temperature-independent background and a narrow Drude-type component which solely determines the transport properties. The narrow Drude subsystem reveals a T2 behavior in the dc resistivity and scattering rate up to room temperature, indicating a Fermi-liquid behavior in this material.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 |