|##author-notes##|
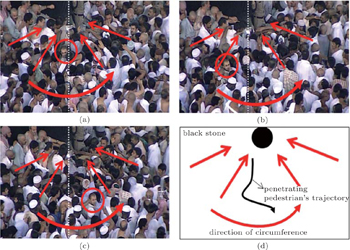
Frozen state from jammed state is one of the most interesting aspects produced when simulating the multidirectional pedestrian flow of high density crowds. Cases of real life situations for such a phenomenon are not exhaustively treated. Our observations in the Hajj crowd show that freezing transition does not occur very often. On the contrary, penetrating a jammed crowd is a common aspect. We believe the kindness of pedestrians facing others whose walking is blocked is a main factor in eliminating the frozen state as well as in relieving the jammed state. We refine the social force model by incorporating a new social force to enable the simulated pedestrians to mimic the real behavior observed in the Hajj area. Simulations are performed to validate the work qualitatively.
Organizing safer mass event is a great challenge to the specialists and authorities in various countries. In critical situations, massive congestion has resulted in disasters, crowd stampedes, serious injuries, and loss of lives.[1–4] Although authorities make careful, well-planned arrangements for offering better pedestrian facilities to ensure the safety of mass crowds, fatal accidents in open areas keep recurring.[5,6] Inappropriate crowd behavior in critical areas in multidirectional flow has been identified as a main reason why such accidents take place. For example, there have been many serious incidents in open areas and multidirectional walkways in Mina during the Hajj, where more than two million Muslims annually perform the stoning rituals.[4] Although Saudi authorities have deployed a considerable amount of effort for improving the Jamarat bridge and the surrounding area in Mina in order to ensure a smooth flow of pilgrims, crowd stampede has occurred recently.[5,6] To recognize the critical crowd behaviors and eliminate the undesirable ones, researchers have been provoked to understand the behaviors of pedestrian traffic flow in multidirectional walkways. Collecting relevant real-life data from empirical studies has become a major concern for analysis and prediction of the crowd behaviors.[4,7] However, there is a lack of resources to provide researchers with such data, which is also limited by photographs and videos. Alternatively, conducting series of experimental studies to explore the aspects of the multidirectional flow has become a big concern. The factors dominating these aspects have been taken in detail in a considerable number of studies, such as the bi-directional flow distributions,[8] avoidance maneuver,[9] the dependence of the arrival time on the density,[10] the effect of look-ahead behavior on the velocity as well as the traffic flow,[11] the effects of the speed variability on the stability of the traffic structure,[12] the order of counter flows on the speed-flow-density relations[13] and the pedestrian flow in multi-intersecting areas.[14] However, for ethical reasons and other difficulties, critical situations which could result in an extreme state (e.g., extreme crowd flow at entrance[3] or stop and go waves[4]) could not be set up.
For this reason, researchers have been motivated to improve simulation models to help simulate the aspects of the multidirectional pedestrian flow and correspondingly examine the solutions for better crowd behavior and environmental design. For the purpose of validation, the simulation models are essentially required to mimic the real aspects of the multidirectional flow behavior and reproduce its characteristics accurately as well. Subjected to this requirement, a variety of simulation models have been developed to reproduce the pedestrian flow aspects.[15–25] The problematic issue to be treated in this article is that the simulation models have produced a freezing transition from the jammed state[26–30] which contradicts our observations from the Hajj crowd (see Figs.
This real observation does not resemble oscillatory flow phenomenon at bottleneck,[31,32] where the penetrating process in the latter phenomenon is due to the pressure from the flow performing the penetration. Moreover, no spatial separation rule as suggested in Ref. [32] was provided for the pilgrims to constitute the lane opposing the counter flow shown in Fig.
Thus, the existing crowd dynamics models do not represent some crowds’ behaviors similar to what happens in real life situations. Our simulation based on the social force model introduced freezing transition as introduced by Helbing et al.[26] We refer the freezing transition to shortcoming from the simulated pedestrians located in a jammed crowd who cannot penetrate the high density crowd in front as well as from the opposing simulated pedestrians who lack the kindness behavior as a social characteristic to make a way for the others who directly face them. The remaining part of this paper is organized as follows. In Section 2, we introduce the social force model. In Section 3, we address the issue of how the penetration process could eliminate freezing transition, and then we propose a refinement of the social force model to enable the penetrating process in jammed crowds. Finally, the relevant simulations to demonstrate the results of our work are performed.
The social force model (SFM) is a continuous-space microscopic simulation model that has been considered as the most realistic model to express the motivations of pedestrians to act as forces. The motion of each simulated pedestrian is subject to a semi-Newtonian equation, where the simulated pedestrian has an acceleration dvi/dt that results from the sum of forces exerted by the surrounding pedestrians and obstacles

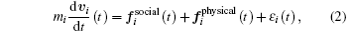

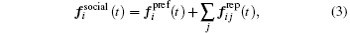
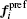
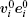
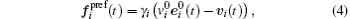
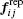
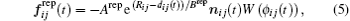
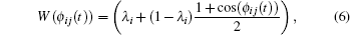
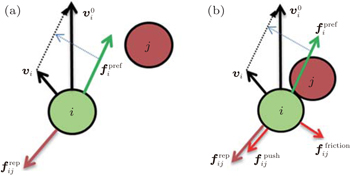 | Fig. 3. (a) The social forces exerted by an object j on pedestrian i are illustrated. (b) The physical forces appear because of the physical contact between pedestrian i and object j. |
The physical forces 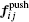
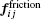

The forces of the SFM are characterized with parameters capable of being formulated to accommodate enormous aspects of crowd dynamics to introduce self-organization phenomena and to reproduce real life data as well.[24,31–34] In Ref. [34], the repulsive distance range Brep was modeled in terms of local density, by reproducing the fundamental diagram conforming to experimental data produced in Ref. [35]

Analogously, the parameter λi was formulated in Ref. [24] in terms of the pedestrian’s local density, based on reproducing realistic flow rate within the range stated in experimental studies as follows:
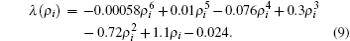
The essential force plays a main role, and for collision avoidance, is the social repulsive force (see Fig.
Strategies of collision avoidance have been incorporated into the social force model by modifying the preferred velocity such as in Ref. [36], adding new forces in Ref. [37] or directing the instantaneous motion toward immediate blank spaces in Ref. [25]. However, these strategies do not play an effective role in the jammed state because of the lack of blank spaces. Therefore, freezing transition could emerge quickly.
Based on the implementation of simulation models, it is observed that the frozen state starts with a small cluster of jammed pedestrians, and consequently the walking of a few of them becomes blocked. With time going by, the cluster becomes large due to extreme jamming and the flow becomes frozen. In our real observations, the single lane in Fig.
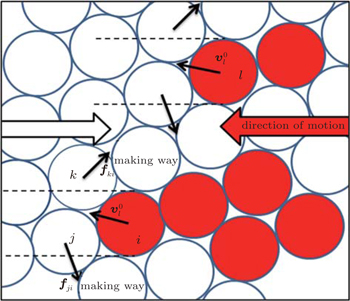
Theoretically, in the SFM, the freezing transition could occur when simulated pedestrians have not appreciated values of forces to penetrate the front of the jammed crowd. Their preferred forces are completely vanished by the numerous encountering forces. The proposed model in this section provides the simulated pedestrians with blocked walking ability of penetrating a jammed crowd and provides his opposing pedestrians with kindness behavior to allow such a penetration. To each stuck pedestrian i we give the notion of his facing pedestrians as the pedestrians opposing him, intersecting his rectangular path along his direction toward his destination, and are in contact. They are almost two, j and k, with respect to pedestrian i as illustrated in Fig.
Basically, we assume that all simulated pedestrians are kind. The stuck pedestrians who are opposing enormous counter flow would lose their respect to the personal areas of the facing pedestrians. The kindness factor αkindness is incorporated into Eq. (
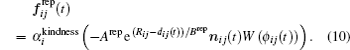
The factor αkindness could be influenced by personal, cultural, or environmental factors. In this work, it is proposed as follows. The factor αkindness equals one for the kind pedestrian, it would slightly decrease for the stuck pedestrian with the decrease in his actual speed Sdest toward his destination, and it would considerably fall to approximately zero when Sdest goes below a threshold value to represent complete loss of patience. The model of αkindness for all pedestrians is introduced in the following form:
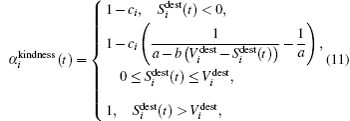
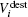

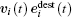

Naturally, making way behavior is a moral response by the kind pedestrians to the voice or bodily cues or pushing from the stuck pedestrian who tries to penetrate the front of the jammed crowd, e.g., declaratively asking way or transgressive walking. Such a behavior is common in areas where religious rituals are performed, for example the Hajj crowd (as illustrated in Fig.
The penetrating pedestrians are specified with a value one for the penetration parameter Pi. The parameter Pi equals zero for the remaining pedestrians. For the penetration process, firstly, we propose that the penetrating pedestrian strengthens his preferred force by increasing his preferred speed and directing his motion toward the weakest point in the front of the jammed crowd to be penetrated, namely, the point of contact between the facing pedestrians j and k (see Fig.
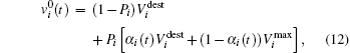
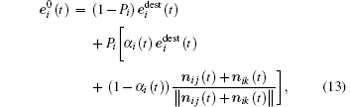
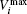
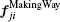
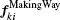
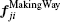

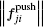


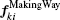


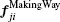
Finally, equation (
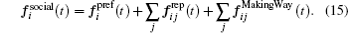
Two scenarios are set up in this section to validate the work of this article. The first scenario is the conduction of simulations to exhibit the ability to simulate pedestrians for penetrating the jammed crowd in normal situations, and the second scenario is an implementation of our work to show its effect on forming lanes.
The setup of the physical environment depicted in Fig.
 | Fig. 6. Snapshots (a)–(d) have chronologically been taken, to capture the penetration of jammed crowd exiting a room. |
| Table 1. Simulation parameters. . |
We choose a = 6.2 and b = 4 based on the obtained αkindness = 0 when the actual velocity of a penetrating pedestrian approaches to zero (see Fig.
As shown in Fig.
It is worth noting here that this penetration process is different from the oscillation phenomenon at a bottleneck, as stated in Ref. [31]. In the latter, the increase in the pressure from the blocked pedestrians can result in the change of the flow direction. However, this is not a matter of pressure; it is a kindness behavior from the pedestrians exiting the room.
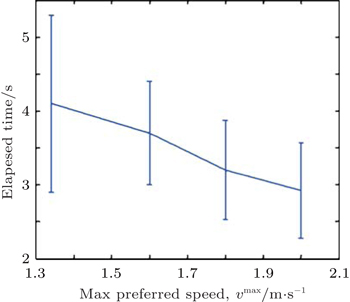
To investigate the dependence of the average time for penetrating the jammed crowd on coefficient F, we chose different values of F for the values a = 6.2, b = 4, and 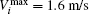
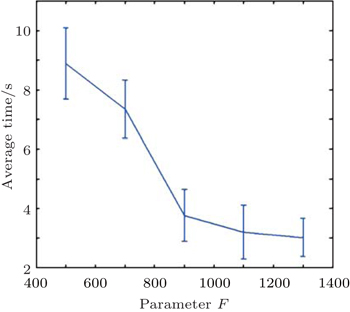 | Fig. 7. Error bars show the means and deviations of the average time plotted as a function of the magnitude of parameter F. |
However, this decrease is not significant for values higher than 900. The last behavior is natural because making way for the penetrating pedestrians is limited to the lack of spaces among the clogging pedestrians. Similarly, we chose different values of 
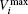
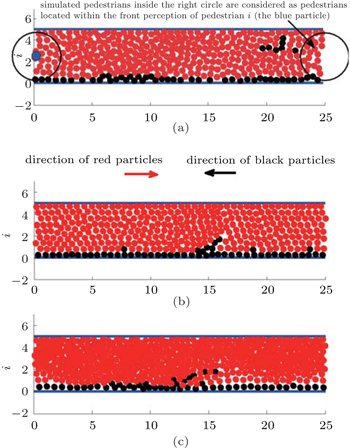
In this subsection, the simulations to exhibit the pedestrian ability to join the lanes are conducted. Investigating the flow of lanes is an intelligent capability proposed in Ref. [39]. The simulated area of the current simulations is a straight walkway (see Fig.
The specification of the simulated pedestrians and their motion are as follows: up to 400 simulated pedestrians are initialized in the walkway and divided into two groups. The positions of the first group of pedestrians were initialized randomly in the walkway simultaneously and their motion instantaneously is directed rightward. The second group is directed to the opposite side; a few of them are initialized in the right-up corner of the walkway randomly and considered as stuck pedestrians, ci = 1, and the remaining pedestrians are initialized as a lane in the lower part.
All simulated pedestrians prefer velocities with a mean of 1.34 m/s and standard deviation of 0.26 m/s. The criterion to validate the above work is the occurrence of joining lanes in jammed situations; that is, the stuck pedestrians from the second group changes their direction and intersects the opposing flow to join the lane below. As shown in Fig.
In this article, penetrating a jammed crowd as a critical crowd behavior is recognized in multidirectional walkways. It is simulated in the social force model by enabling the stuck pedestrians to penetrate the front of a jammed crowd. Kindness behavior (such as making way) from the facing pedestrians toward the stuck pedestrian is an essential factor for the penetration process. With this representation, freezing transition introduced by many simulation models can be eliminated. The representation of real behavior observed in the Hajj crowd is used as a qualitative validation of this work. The result is consistent with the experimental studies which handle multidirectional flow aspects.
The contribution in this article gives researchers an insight into the crowd behavior, which helps eliminate the undesirable ones. It can be easily extended to many aspects of pedestrian flow by considering different orderings of multidirectional flow and incorporating some aspects involving physical characteristics such as obstacles and walls. Having techniques that can offer a nearly optimal parameter value is necessary. We recommend devoting more effort to the development and the implementation of these techniques for the calibration of our proposed model.
It is hoped that this work will be of particular benefit to those who are involved in the applications of organizing safer mass events such as the Hajj crowd.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 |