Chaos phenomenon has been extensively studied by many researchers due to its complicated and unstable behavior and wide range of applications in many industrial systems and different sciences. In recent years, various types of chaotic systems have been introduced and investigated due to the great importance of this phenomenon.^[1,2] In chaotic systems, a very small difference in the initial conditions leads to a major difference in system states. Thus, such extreme sensitivity to the initial conditions complicates its control in many practical systems. Numerous advanced control methods, such as sliding mode control (SMC), fuzzy control (FLC), etc., have been proposed to address the problem of control and synchronization of the chaos phenomenon in many applications.^[3–7]

The sliding mode control method is a simple and robust control method for a nonlinear system, which is an appropriate method to solve stability problems confronting uncertainties in a system model. This control method has considerable characteristics such as simple design, easy implementation, low cost, and robustness against uncertainties.^[5]

In recent years, the idea of sliding mode control and the definition of a sliding surface to which the system states can be converged and the system stability can be guaranteed, has led to the formation of other similar methods, such as terminal sliding mode control (TSMC), integral sliding mode control (ITSMC), and other analogous combinations.^[8,9] In these methods, the particular definition of the sliding surface is considered to control the system.

The TSMC is a method for controlling systems based on the definition of a terminal sliding surface, which is defined as an exponential nonlinear function. This method provides faster convergence of system states to the sliding surface in comparison with the conventional SMC method owing to the structure of its surface.^[8] The TSMC method is divided into different branches, each of which has been proposed because of a specified control objective.^[10,11]

For instance, in Ref. [12], first-order TSMC has been applied to second-order nonlinear systems. In Ref. [13], Yu and Man have extended the TSMC method to high-order linear single input-single output systems. Later, a general TSMC method has been introduced for linear multi input-multi output systems. Afterwards, Yu and Mann have proposed fast TSMC (FTSMC), which profits the ability of fast convergence of states to the sliding surface.^[14,15]

In Refs. [16] and [17], nonsingular TSMC (NTSMC) has been suggested, which prevents the occurrence of singularity. In the subsequent years, the TSMC has been combined with other concepts and methods, leading to nonsingular fast TSMC (NFTSMC) for second-order systems.^[10] This new method provided both characteristics of high speed and avoiding singularity.^[10] In the following studies, such as in Ref. [8], the NTSMC method with finite-time convergence has been proposed for two classes of high-order nonlinear and non-autonomous systems.

To summarize the advantages and disadvantages of the TSMC methods, it can be stated that nonsingular methods do not possess the feature of finite-time convergence, and provide a lower convergence speed compared with the FTSMC methods. However, the FTSMC method has a major defect, i.e., the possibility of the occurrence of singularity in system control. Moreover, the NFTSMC methods have been introduced for second-order systems frequently, and the control of high-order systems has not been accomplished by this kind of control method. Furthermore, in the method proposed in Ref. [8], despite suggesting a nonsingular and finite-time control method for high-order systems, external disturbances and compatible additive uncertainties have not been considered. Though this problem has been solved in Ref. [6], which provides the benefits such as finite-time convergence, considering disturbance, uncertainty and generalization of the method for high-order systems. In spite of all the benefits of the TSMC method introduced in Ref. [6], one of its major weaknesses is the occurrence of a chattering phenomenon.^[6,18] Hence, by applying methods based on the sliding surface and by profiting positive features of these methods along with solving their serious problem such as the chattering phenomenon, an effective control system can be proposed.

In this paper, an ITSMC is designed in order to control the chaos in a rod-type plasma torch system in the presence of uncertainty and external disturbance. The proposed method is designed in order to eliminate the chattering phenomenon along with a high response speed, whose sliding surface is proposed for the first time. Primarily, a controller is suggested based on ITSMC to stabilize the system on the basis of Lyapunov theory. The sliding surface proposed for this method is a combination of the sliding surface of TSMC and a nonlinear function of the integral of system states. The reasons for defining such a sliding surface are the proper response speed, chattering rejection, and robustness against external disturbances. Nonetheless, this method will not be efficient, if a part of the system dynamics is unknown and only a part of input–output information is accessible. In these cases, another method must be utilized based on approximation of unknown dynamics. Thus, when the nonlinear dynamic of the system is unknown and only its input–output information is accessible, an intelligent ITSMC (IITSMC) is designed for the first time in this paper, which is a combination of ITSMC and an adaptive neuro fuzzy inference system (ANFIS), and is used to stabilize the plasma torch system. ANFIS is applied to approximate a part of the nonlinear dynamic that is unknown. Via this approximation, a suitable controller can be designed in order to stabilize the plasma torch system, which indicates a special class of chaotic systems. With the purpose of improving the control performance, a bee algorithm is utilized to choose the coefficients of the ITSMC.

The advantages of the proposed method are high speed convergence and chattering-free response, which are the results of selecting a new sliding surface. In addition, the introduced approach is capable of stabilizing the system in the presence of model uncertainties and disturbances when the nonlinear dynamic of the system is unknown. The proposed method due to the application of ANFIS for the approximation of nonlinear dynamics, gives a good response with very low oscillations. In fact, designing this intelligent combined controller improves all the desired control objectives, such as the settling time of system states, transient response, chattering problem, and system response in the presence of model uncertainties. With the aim of comparing the proposed control method with previous classic control methods, such as TSMC, both methods are implemented on a rod-type plasma torch system. Simulation results illustrate the efficiency and appropriate performance of the proposed control method.

The paper organization is as follows. In Section 1, the studied plasma torch system is described. The ITSMC is introduced in Section 2. In Section 3, the proposed IITSMC method is explained. Section 4 includes the simulation results, and finally, the conclusions are drawn in Section 5.

A plasma torch system or plasma thermal gun, which is widely used in industrial applications today, is a system with a chaotic nature, and chaos control can improve its efficiency in industrial procedures, such as metal cutting and spraying molten metals on different surfaces.^[19,20] Two of the major challenges in these industrial operations are accuracy and high quality. Obviously, the occurrence of chaos in such systems will reduce the quality of the final product. Therefore, controlling the undesired chaos phenomenon is one of the most important objectives and problems in the control of plasma torch systems.

In this paper, according to the studies in Refs. [19] and [21]– [23], a class of third-order nonlinear equations are considered for probable determination of the gap phenomenon. The mathematical model of the plasma torch system can be written as

Considering F = X₁, Ḟ = X₂, and F̈ = X₃, the system (1) can be rewritten in the following form:

The equilibrium points of the system are [0 0 0]^T for μ < 0 and , which are stable for 0 < μ < 50 and −25 < μ < 0, respectively. Based on Ref. [18], by reducing the value of system parameter μ, the plasma torch system behaves chaotically. Besides, on the basis of bifurcation and maximum Lyapunov exponent analyses in the same research, by considering the system parameter as μ = − 130, the system states will have chaotic behavior, and the zero equilibrium point of the system will become unstable.^[20] The phase portrait of the system is demonstrated in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The phase portrait of rod-type plasma torch system.

By adding disturbance and compatible additive uncertainty to the third term of the state equations of the system and by applying a control signal in order to control the chaos and stabilize the unstable equilibrium point, the plasma torch system is expressed as

Disturbance and uncertainty reduce the quality of the processes, such as cutting and covering metal surfaces, in the plasma torch system. Disturbance is a sudden change in system operation conditions, which can lead to instability. Uncertainty indicates unmodeled dynamics that are inevitable in most of the systems. From a practical point of view, the initial process leads to extremely small disturbance in the system.^[19] Additionally, there exists a grey probe in the plasma torch to bring out the gas sample, whose direction can cause disturbance in the system.^[24] The inequalities |d(t)| < γ and | Δf| < α are assumed for disturbance and compatible uncertainty, respectively.

The control signal u(t) is applied to the system in order to achieve the following stabilization condition:

The system equations can be rewritten as

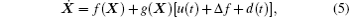
As it is known, the TSMC method is a powerful method from several aspects, such as a desirable settling time, robustness against bounded uncertainties, and external disturbances, simplicity in design and implementation. However, its main problem is chattering, which is undesirable in control systems, and must be eliminated via the proper method. Consequently, in this paper, the idea of combining the terminal sliding surface with an integral function is proposed. The objective of selecting this structure for sliding surface, is to provide a high response speed, chattering elimination, and robustness against external disturbances. The proposed method is designed by assuming that the dynamics of the chaotic system are known and the system is exposed to disturbance and compatible uncertainty. In the proposed ITSMC method, a new equation is suggested for a sliding surface for the first time, which is a combination of the sliding surface of the TSMC method and a nonlinear function of the integral of system states. Furthermore, in order to achieve accurate results, the parameters of the controller are calculated by the bee algorithm.

The design of ITSMC consists of two main steps: selection of an appropriate sliding surface and definition of a control law, which is comprised of equivalent and discontinuous control parts. The equivalent control guides the system states onto the sliding surface, while the discontinuous control conveys the system trajectories to reach the sliding surface, and keeps them on the surface.

The system (3) can be rewritten as

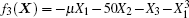
The subsequent equation is proposed as the sliding surface

The sliding surface proposed in Eq. (8) is considered as a combination of the sliding surface of the discussed ITSMC and an integral function of system states, where 1 < β < 2. The reasons for this selection of sliding surface are to reach a high convergence speed owing to the terminal sliding mode part, and a reduction of convergence error of system states due to the integral part. The range chosen for β is because of increasing the convergence speed.

With the purpose of obtaining an appropriate control law, firstly, the equivalent control law is attained in the way that when the chaotic system reaches the sliding surface it stays on it. The following two equations are satisfied:

Afterwards, the control law of integral TSMC must be determined so that it can convey the chaotic system states to sliding surface S(t) = 0. When the controlled system is on the sliding surface, the condition Ṡ(t) = 0 must be satisfied. Hence, in absence of uncertainty and disturbance, according to Eq. (11), the equivalent control law u_eq can be obtained as

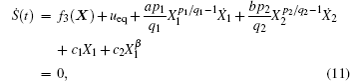
Furthermore, to tackle the effects of uncertainty and disturbance, the control law is expressed as

Therefore, the total control law that takes the system states to the sliding surface and preserves them on it is obtained as

In order to select the controller coefficients with high accuracy compared to the trial and error method, a bee algorithm is utilized, which is introduced in Appendix A.

To demonstrate that the control law (14) possesses the capability of conveying the states of the chaotic system (6) to the sliding surface S(t) = 0 in the presence of disturbance and uncertainty, Theorem 1 is proposed.

Theorem 1 By considering the system with uncertainty (7), the control law (14), the integral terminal sliding mode surface (8), and the condition K_ITSMC > α + γ, the trajectories of the chaotic system converge to the following terminal sliding surface:

Proof In order to prove the stability of system (7) with control law (14), Lyapunov stability theory is used. For this purpose, the following Lyapunov function, which is a positive definite function, is considered

The time derivative of this function is

According to the range of disturbance and uncertainty of Eq. (7), it can be concluded that

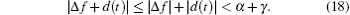
As we have S sgn(S) = |S|, the following equation will be obtained according to Eqs. (17) and (18):

By assuming the bottom condition, the condition V̇ < 0 will be satisfied, and the trajectories of the chaotic system will converge to the sliding surface S(t) = 0

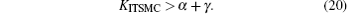
As discussed in the previous section, the stability condition of the ITSMC method is described by inequality (20). Despite the capabilities of this method in stabilizing the system with high speed and without chattering, if precise information about the bounds of uncertainties and external disturbances is not accessible, it will not be effective and applicable. Moreover, the implementation of this method requires an accurate model of the system. Thus, when an exact model of the system is not accessible, and merely a limited set of input–output data of the unknown dynamic of the system is available, we need a new approach that has the capability of controlling the system with a good, fast and chattering-free response, and can be highly flexible against external disturbances and model uncertainties. In other words, a system must be applied to approximate the unknown part. Accordingly, in this section, the IITSMC method is designed for a plasma torch system, when a part of the system dynamics is unknown.

In the proposed IITSMC method, the sliding surface is considered as similar to the surface of the method studied in the preceding section, which is a combination of the sliding surface of the TSMC method and a nonlinear function of the integral of system states. In order to preserve the earlier control objectives, such as a desirable settling time of states, chattering elimination, improvement of transient response, and proper response in the presence of model uncertainties, the idea of combining ITSMC and ANFIS is proposed. The ANFIS is designed to approximate the unknown part of the system, to omit the unknown nonlinear terms in the derivative of the Lyapunov function, and to overcome the disturbance and uncertainty. Besides, the remaining dynamic is converged to the equilibrium point via the ITSMC. Figure 2 shows the block diagram of the designed combined controller.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Block diagram IITSMC based on ANFIS.

The design of IITSMC consists of two main steps as well: selection of a suitable sliding surface and definition of the control law. The system (7) can be rewritten as

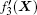
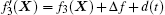
The proposed novel sliding surface is expressed as

In Eq. (21), is an indefinite function, and in Eq. (22), the exponents p₁, q₁, p₂, and q₂ are odd positive numbers satisfying the conditions p₁ > q₁ and p₂ > q₂. In addition, a b, c₁, c₂, and β are design parameters.

The proposed sliding surface (22) is a combination of the sliding surface of the TSMC^[8] and an integral function of system states. As mentioned in the previous section, the reasons for selecting this sliding surface are achieving a high convergence speed due to the terminal sliding mode part, and reduction of convergence error of the system states owing to the integral part. Moreover, β is a design parameter, where its range is considered as 1 < β < 2.

The control law of this method is a combination of ANFIS control law and ITSMC, which is obtained from system Lyapunov function.

By assuming the sliding surface (22), its time derivative becomes

Due to the approximation property of ANFIS,^[25] this system is capable of approximating an arbitrary defined continuous function f on a compact set with a satisfactory accuracy, which is shown with f̂. In fact, by selecting enough numbers of membership functions for input space, there will be a limit on approximation error e via ANFIS. This limit is defined as ε(ε → 0),^[26] so that

According to the system characteristics, is unknown. Function f must be approximated and considered as

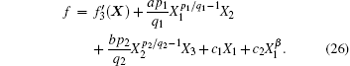
If ANFIS approximates the function (26), and u_ANFIS is considered as a control signal that applies the negative approximated function to the system, the remaining dynamic can be stabilized by u_ITSMC. Indeed, there is a set of inputs and outputs for unknown functions that are utilized for the training of ANFIS, firstly. The initial training is for preventing the increase of approximation and convergence times of the closed-loop control system states. Then, the trained network is placed in the closed-loop control system, and its weights update simultaneously with ITSMC’s work. Hence, u_ANFIS is a signal that is approximated online via the ANFIS.

In Eq. (26), is unknown, and thus f is not known either. Furthermore, in Eq. (27), f̂ is an online approximated signal by the ANFIS. Now, according to Eqs. (23)–(27), the following equation is obtained:

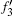
Hence, according to Eqs. (25) and (28), the following equation is concluded:

Now, the remaining dynamic in an intelligent combined controller must be stabilized by the ITSMC signal. ANFIS can overcome the effects of uncertainty and disturbance. If u_ITSMC is considered, the system will converge to the sliding surface S(t) = 0

The ANFIS can overcome the effects of uncertainty and disturbance and thereby large gain is not needed to tackle such effects. This leads to a considerable reduction in chattering. Therefore, the general control signal that conveys the system to the sliding surface and preserves it on it can be expressed as

In order to depict that the control signal (30) is capable of conveying the states of the chaotic system (31) to the sliding surface S(t) = 0 described by Eq. (22), the following theorem is proposed.

Theorem 2 By considering the chaotic system (21), the control law (30), the integral terminal sliding mode surface (22), the approximation error (25), and the condition K_ITSMC > ε, the trajectories of chaotic system converges to the following terminal sliding surface:

Proof With the aim of proving the stability of system (21) by control law (30), the Lyapunov stability theory is utilized. For this reason, the following positive definite Lyapunov function is considered:

By computing the time derivative of Lyapunov function (33), we have

Consequently, according to Eq. (25), we will have

Then, the derivative of the Lyapunov function is obtained as

As S · sgn(S) = |S|, then the following equation is obtained:

Thus, the condition V̇ < 0 is satisfied, and it means that the trajectories of the chaotic system converge to the sliding surface S(t) = 0. It can be shown that the convergence will be reached in a finite time.

At the convergence time, we have S(T) = 0. By integrating two sides of Eq. (34) from zero to the convergence time T, we have

Therefore, according to Eq. (42), we have

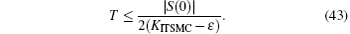
Therefore, it is concluded from the above equation that S converges to zero (S → 0) in a finite time.

The structure of the ANFIS and training rules are explained in Appendix B.

In this section, simulation results are given to verify the applicability and effectiveness of the proposed control methods discussed in previous sections.

At first, previous methods applied to the plasma torch system, the SMC and TSMC are simulated separately according to Refs. [6] and [20]. Then the results for the proposed method in this paper (ITSMC and IITSMC) are shown in order to compare with the results of previous methods.

The parameters of the SMC and TSMC are selected according to assumptions in Refs. [6] and [20].

The initial conditions are considered as [5 −2 3]^T, the parameter of the system is considered as μ = − 130, the system is exposed to external disturbance, and has uncertainty. The pulse signal with an amplitude of 5 and a width of 0.3 s, from 5.6 to 5.9 s, is applied to all methods as an external disturbance d(t). Besides, compatible additive unstructured uncertainty Δf in closed-loop systems with these controllers is considered as a sine signal

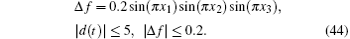
The values of the exponents of the sliding surface in ITSMC and IITSMC is selected as below in the controllers

In order to select the coefficients of ITSMC, the bee algorithm, which is described in the appendix A, is utilized. The parameters of its cost function are considered to be

The parameters of the ITSMC, which are calculated by the bee algorithm, are obtained as

Also, the parameters of IITSMC, which are calculated by the bee algorithm, are obtained as

In addition, it is assumed that an adequate set of data is accessible from the unknown function (26) that is used for ANFIS initial training.

Figure 3 shows the simulation results for SMC implemented on the plasma torch system in the presence of disturbance and uncertainty, according to Ref. [18]. As it is observed, the response has high chattering, which is undesirable for this system. Also, the settling time of the system states is not satisfactory.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Time response of states (a) x1, (b) x2, (c) x3, and (d) control signal with SMC in the presence of uncertainty and disturbance with μ = −130 and initial condition [5 −2 3].

In order to improve the chattering problem and response speed, in Ref. [6] the TSMC has been designed for the plasma torch system. As shown in Fig. 4, the settling time of states is desirable. However, the response still has chattering. This problem is solved in the controller designed in this paper.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Time response of states (a) x1, (b) x2, (c) x3, and (d) control signal with TSMC in the presence of uncertainty and disturbance with μ = −130 and initial condition [5 −2 3].

To solve the chattering problem in the plasma torch system, we apply the proposed ITMC described in the previous section. As shown in Fig. 5, the ITSMC has stabilized the system in the presence of external disturbance and uncertainty. The response speed is acceptable, and the chattering is eliminated completely. Hence, the problems of the previous methods have been resolved by the method presented in this paper. Chattering has been removed and the response speed has been desirable. In addition, the classical ITSMC method implemented in this paper is much easier than the fuzzy methods proposed in Refs. [6] and [20].

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Time response of states (a) x1, (b) x2, (c) x3, and (d) control signal with the ITSMC in the presence of uncertainty and disturbance with μ = −130 and initial condition [5 −2 3].

When the dynamics of the system is partly unknown, the proposed IITSMC in this paper can be applied to the system. As shown in Fig. 6, the IITSMC has stabilized the system in the presence of external disturbance and uncertainty. The response speed is acceptable, and the chattering is eliminated completely. The transient response is good as well. In fact, this controller is capable of controlling the system in the presence of model uncertainties and unknown dynamics.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Time response of states (a) x1, (b) x2, (c) x3, and (d) control signal with IITSMC in the presence of uncertainty and disturbance with μ = −130 and initial condition [5 −2 3].

In this paper, ITSMC and ANFIS-based IITSMC have been designed to control the chaotic plasma torch system. The main objectives of designing ITSMC are to achieve chattering elimination, a satisfactory response speed, robustness against disturbances, compatible additive unstructured uncertainties and the desirable transient response. The considered sliding surface has been considered as a combination of the sliding surface of TSMC and an integral function of system states, which has been proposed in this paper for the first time. However, in the situations that a part of the system dynamics is unknown and merely the input–output information is accessible, this method is not efficient anymore. Hence, in the next step, IITSMC with the same sliding surface considered in the previous step has been designed for the system, in which the IITSMC has been combined with ANFIS. The goal of this combination is that the unknown nonlinear dynamic of the system be approximated by the ANFIS, and the IITSMC stabilizes the system with approximated dynamic. Furthermore, in order to increase the accuracy of the response, the parameters of the sliding surface and the controller have been calculated by the bee algorithm. The comparison of the ITSMC method proposed in this paper with SMC and TSMC,^[6,20] which have been implemented on the plasma torch system previously, illustrates that the designed ITSMC provides better performance with respect to prior methods. The response speed has been improved, and the chattering phenomenon has been eliminated without requirement of the design of a fuzzy controller. Also, when a part of the system dynamic is unknown, and only a set of input–output information is accessible, the IITSMC designed in this paper will be efficient. By having input–output information and without access to the whole dynamics of the system, satisfactory control of the system and achieving desirable control aims are possible via the proposed intelligent method. The simulation results show that the response is suitable and fast, the chattering is omitted, and the transient response is appropriate. In addition, the methods discussed in this research are applicable to any other continuous chaotic system.