Cite this Article
Zhao Qi-Feng, Zhuang Yi-Qi, Bao Jun-Lin, Hu Wei. Radiation-induced 1/f noise degradation of PNP bipolar junction transistors at different dose rates. Chinese Physics B, 2016, 25(4): 046104  
Permissions
Radiation-induced 1/f noise degradation of PNP bipolar junction transistors at different dose rates
Zhao Qi-Feng1, Zhuang Yi-Qi1, Bao Jun-Lin1, †, , Hu Wei2
School of Microelectronics, Xidian University, Xi’an 710071, China
School of Mechano-Electronic Engineering, Xidian University, Xi’an 710071, China

 

† Corresponding author. E-mail: baoing@126.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 61076101 and 61204092).

Abstract
Abstract

It is found that ionizing-radiation can lead to the base current and the 1/f noise degradations in PNP bipolar junction transistors. In this paper, it is suggested that the surface of the space charge region of the emitter-base junction is the main source of the base surface 1/f noise. A model is developed which identifies the parameters and describes their interactive contributions to the recombination current at the surface of the space charge region. Based on the theory of carrier number fluctuation and the model of surface recombination current, a 1/f noise model is developed. This model suggests that 1/f noise degradations are the result of the accumulation of oxide-trapped charges and interface states. Combining models of ELDRS, this model can explain the reason why the 1/f noise degradation is more severe at a low dose rate than at a high dose rate. The radiations were performed in a Co60 source up to a total dose of 700 Gy(Si). The low dose rate was 0.001 Gy(Si)/s and the high dose rate was 0.1 Gy(Si)/s. The model accords well with the experimental results.

PACS: 61.80.–x;61.80.Ed;85.40.Qx
Keyword:radiation;1/f noise;bipolar junction transistors
1. Introduction

The PNP bipolar junction transistors are utilized in analog IC applications such as input stages, active loads, and current sources. Owing to surface effects, some types of PNP bipolar junction transistors are known to exhibit extreme sensitivities to ionizing radiation.[1] For many current bipolar linear technologies, the primary failure mechanism is the reduction of the current gain.[2–4] In 1991, it was found that bipolar junction transistors may exhibit the enhanced low dose rate sensitivity (ELDRS).[5] Since its initial report, all aspects concerning this effect (mechanism, modeling, testing, and recently studied ELDRS) has comprehensively been analyzed.[6–17] However, most of the radiation studies of Si bipolar junction transistors reported so far have mainly focused on experimental results about the radiation-induced changes in the measured electrical characteristics of the devices. To the authors’ knowledge, very little data regarding 1/f noise performance degradation with the total dose and the dose rate have been reported for Si bipolar junction transistors.[18,19]

The total dose 1/f noise performances of PNP bipolar junction transistors radiated at different dose rates are presented. Based on the theory of carrier number fluctuation, a model is developed which identifies the physical mechanism responsible for the 1/f noise degradation. The model suggests that the 1/f noise degradations can be attributed to the accumulation of oxide-trapped charges and interface states. Combining models of ELDRS, the 1/f model can explain the reason why the 1/f noise degradation is more severe at a low dose rate than at a high dose rate. This work utilizes experiments and an analytical model to explain the mechanism responsible for radiation-induced 1/f noise degradation.

2. Model
2.1. Model of recombination current at the surface of the space charge region

When the base- emitter is under forward bias, the difference in quasi-Fermi energy level between electrons ɛFn and holes ɛFp is related to the voltage VEB applied to the Base-Emitter junction, that is, ɛFn − ɛFp = qVEB,[20] where q is the electron charge. The carrier concentrations in the space charge region are given by

where ɛFix is the intrinsic Fermi level in the space charge region, k is the Boltzmann constant, T is the absolute temperature, ni is the intrinsic carrier concentration, n(x) is the electron concentration, and p(x) is the hole concentration.

The origin of the x axis is at the edge of the space charge region on the p side as shown in Fig. 1. In Fig. 1, EC is the energy level of the Si conduction band bottom, EV is the energy level of the Si value band top, and ɛFi is the intrinsic Fermi level. At the origin of the x axis, the intrinsic Fermi level is ɛFi0 which we defined to be zero. From Fig. 1, it can be seen that the intrinsic Fermi level in the space charge region can be written approximately as[20]

where W is the space charge region width; x is located in a range: 0 ≤ x ≤ W; V0 = VFn − VFp is the built-in voltage, with VFn = kT ln(ND/ni)/q being the Fermi potential in the base, ND the doping concentration at the base. VFp = kT ln(ni/NA)/q the Fermi potential in the emitter, and NA the doping concentration at the emitter.

Fig. 1. Energy level of p–n junction under forward bias.

At x = 0, the hole concentration is given by

At x = W, the electron concentration is given by

From Eq. (4) we can obtain an expression for ɛFp:

From Eq. (5) we can obtain an expression for ɛFn:

In most analytical treatments of recombination in the space charge region, the spatial dependence is neglected;[4] instead, it is usually assumed that the total recombination rate can be obtained from the behavior of the peak recombination rate. However, in a radiated polar junction transistor, this assumption is subject to important limitations.[21] It is necessary to include the recombination current throughout the surface of the space charge region of the emitter-base junction to adequately describe the effects of radiation. The recombination current at the surface of the space charge region may be calculated by integrating the recombination rate over the surface of the emitter-base space charge region. It can be given by

where L is the emitter perimeter, s = vthσsNit is the surface recombination velocity, Nit is the interface trap density, σs is the trap cross section, vth is the electron thermal velocity, ns is the surface electron concentration, and ps is the surface hole concentration.

For a PNP bipolar junction transistor, an oxide-trapped charge causes the surface region of an n-type base to fall into accumulation. As the base is usually in accumulation mode, the following correlation between the surface potential Vs and oxide-trapped charge Not is valid:[22]

We assume that the surface potential at the surface of the space charge region is approximately equal to the surface potential at the surface of the base. The surface potential would make the potential at the surface of the space charge region bend. At the same time, the accumulation of the base forces a reduction in the width of the space charge region at the surface as shown in Fig. 2. A reduced width of the space charge region can be given by

Fig. 2. Cross-section of the emitter base junction, illustrating accumulation regions in the presence of positive oxide charge.

The carrier concentrations at the surface of the space charge region can be given by

Combining Eqs. (1), (3), (7), and (11), the surface recombination becomes

Combining Eqs. (2), (3), (6), and (12), the surface recombination becomes

The surface recombination can be expressed by

Combining Eqs. (13), (14), and (15), the surface recombination becomes

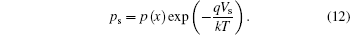
Assuming VBE > 4kT/q, equation (16) is rewritten as

Substituting Eq. (17) into Eq. (8), equation (8) becomes

where

Equation (18) is the expression of the recombination current at the surface of the space charge region.

The opposing nature of oxide charge and interface traps may be verified with the aid of Fig. 3 which shows contour plots of the base surface recombination current Is with surface recombination velocity and oxide charge as parameters on the y and x axes, respectively. As the surface recombination velocity is increased by one order of magnitude, the base surface recombination current increases approximately one order of magnitude. However, as oxide-trapped charge density is increased by one order of magnitude, the base current varies (reduces) much less than one order of magnitude. Therefore, the change in the surface recombination velocity will dominate the base surface recombination current response.

Fig. 3. Contour plots of base surface current response to an interactive combination of surface recombination velocity and oxide charge density.
2.2. Model of base surface 1/f noise

The low frequency 1/f noise in a bipolar junction transistor is currently explained by the fluctuations in carrier number[23–25] or Hooge Mobility.[26,27] It is generally admitted that the variation of power law exponent α of the current noise with the dc current provides the information about the noise type. When the exponent α is close to unity, the Hooge mobility fluctuations are believed to be responsible for the low frequency noise, while α ≈ 2 is indicative of carrier number fluctuations. Several 1/f noise models of a bipolar junction transistor were introduced in detail in Ref. [28]. For a bipolar junction transistor, the base current fluctuations are decomposed into surface and volume originated noise sources.[29] Often the surface 1/f noise component is the dominant component of the base 1/f noise.[30]

Experimentally, 1/f spectra have been observed in one or more tens of frequency ranges, requiring a process characterized by a time constant distributed over a wide range. Based on the theory of carrier number fluctuation,[31] there are two classes of carrier traps near the Si–SiO2 interface, that is, oxide-trapped charges and interface states. The interface states exchange carriers with the conduction band or valence band of silicon as the generation-recombination centers due the SRH process, and, only a definite time constant is observed for interface states at a given energy. The oxide-trapped charge can exchange the carrier with the conduction band or valence band of silicon through the trap-tunneling process. The interface states are distinguished from the oxide-trapped charges by their location, thus by their shorter relaxation time constant than those of the oxide-trapped charges. Therefore the interface states contribute to relatively high frequency components of noise compared with the oxide-trapped charges whose time constants are longer than those of the interface states and have a wide range of time constants, which are necessary to generate a 1/f noise spectrum. So, the base surface 1/f noise of a PNP bipolar junction transistor may be ascribed to the low frequency fluctuations in the surface recombination current due to the dynamic trapping–detrapping of carriers into oxide-trapped charges.

The dynamic trapping–detrapping of carriers into oxide-trapped charges causes an oxide-trapped charge fluctuation δNot, which should lead to a base surface current fluctuation δIs. According to Eq. (18), the fluctuation in the base surface recombination current is given by

Combining Eqs. (9), (10), (18), and (19), equation (19) turns into

where

According to Eq. (20), the 1/f noise power spectral density of the base current is given by

where SNot = kTλNt (E)/(LW f)[30] is the oxide-trapped charge spectral density, with Nt(E) being the number of oxide-trapped charges per unit volume per unit energy (/eV/cm3), and λ the attenuation tunneling distance; Not (E) = λNt (E) is the number of oxide-trapped charges per unit area and per unit energy interval (/cm2/eV), and Not(E) is often continuously distributed in the forbidden gap. The Not can be obtained by integrating over the whole energy range

As the energy distribution of oxide-trapped charges is now not completely determined,[32] we make a simplified assumption that Not(E) is uniformly distributed over the whole energy range, and expressed as

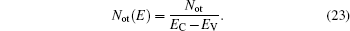
Then the correlation between Nt(E) and Not can be obtained as follows:

Combining Eqs. (21), (23), and (24), the 1/f noise power spectral density can be expressed as

Equation (25) shows that the accumulation of oxide-trapped charges Not and interface states Nit brings about changes in the base current noise.

3. Experiment and discussion
3.1. Experiment

The devices studied in this work were vertical PNP bipolar junction transistors obtained from a semiconductor manufacturer in China. Each device had an emitter with a doping surface of 1 × 1020 cm−3, and the base doping is 1 × 1017 cm−3. All transistors were irradiated with ionizing gamma-radiation from a Co60 source at room temperature. The low dose rate was 0.001 Gy(Si)/s and the high dose rate was 0.1 Gy(Si)/s. The parameters of the transistors were measured prior to and after 100, 300, 500, and 700 Gy(Si) of total dose exposure. The measured electrical parameters were the base current IB and the collector current IC, which were measured by an HP4156 Semiconductor Parameter Analyzer. The common emitter configuration circuit was used for noise measurements as shown in Fig. 4. Batteries were used to bias the base and collector terminals. The base load resistance RB ≫ rπ was connected in series with the base (here rπ = dVBE/dIB is the input base emitter resistance, IB is the collector current). The noise signal SVC from the collector load resistor RC was amplified with a PARC113 low noise amplifier and then measured with an XD3020 noise measurement system which was described in Ref. [33]. In this high impedance model of operation, the base current noise SIB makes the main contribution to the output noise SVC, and is expressed as[34]

where β (β = IC/IB) is the current gain and IC is the collector current.

Fig. 4. Circuit used to bias the transistor for noise measurements.
3.2. Results and discussion

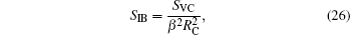
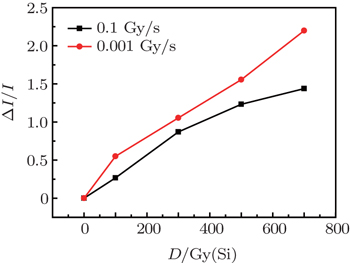
The relative change in the base current, ΔI/I0, is plotted versus total dose in Fig. 5. Figure 5 shows that ΔI/I0 increases with total dose increasing. The base current degradation mechanism can be explained as follows. With the accumulation of total dose, the oxide-trapped charges and the interface states increase. As recombination centers, the interface states cause the surface recombination rate to increase, which makes the base surface recombination current increase. However, for a given surface recombination velocity, the oxide-trapped charges lead to a reduced recombination rate at the surface. The oxide-trapped charges accumulate in the surface of the base and force the holes to enter into the subsurface, which results in the decrease of recombination current. At the same time, the accumulation causes the width of the space charge region at the surface to decrease, which results in a lessening of the area for recombination current. As the surface recombination velocity is increased by one order of magnitude, the base surface recombination current increases approximately one order of magnitude. However, as oxide-trapped charge density is increased by one order of magnitude, the base current varies (decreases) much less than one order of magnitude. Therefore, the change in the surface recombination velocity will dominate the base surface recombination current response.

Fig. 5. Normalized base currents versus total dose.

Figures 6(a) and 6(b) show the base current noise spectra SIB of the samples radiated at the dose rates of 0.1 Gy(Si)/s (Fig. 6(a)) and 0.001 Gy(Si)/s (Fig. 6(b)). Figure 6 shows that the low frequency noise performances are degraded significantly with accumulated total dose at the same rate for frequencies below 100 Hz.

Fig. 6. Base current noise spectra versus total doses of (a) 0.1 Gy(Si)/s and (b) 0.01 Gy (Si)/s.

The power spectral density of the base current is commonly expressed as follows:

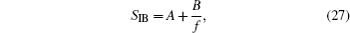
where A is the amplitude of white noise (A2/Hz) and B is the amplitude of 1/f noise (A2/Hz). In Eq. (27), A and B may be extracted respectively from the measured noise spectrum by using the least-square fitting. In a frequency range of 10 Hz–100 Hz, the white noise is usually negligible.

From Eqs. (25) and (27), B can be obtained as

The amplitude of 1/f noise B is used to evaluate the base current noise degradation. The relative change of B can be written as

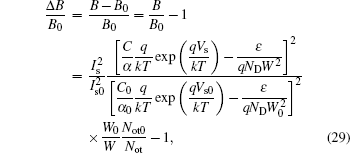
where B0, Nit0, Vs0, W0, Not0, C0, and α0 are the pre-radiation parameters, B, Nit, Vs, W, Not, C, and α are the post-radiation parameters.

From Eq. (18), we can obtain

Combining Eqs. (29) and (30), we can obtain

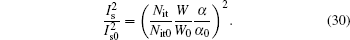
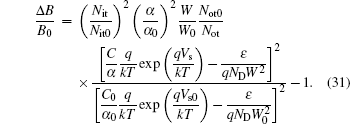
The plots of relative change in the amplitude of 1/f noise, ΔB/B0, versus absorbed dose under radiations at two dose rates are shown in Fig. 7. Figure 7 shows that ΔB/B0 increases with total dose increasing at the same rate, and at the same total dose level ΔB/B0 changes faster at the dose rate of 0.1 rad(Si)/s than at the dose rate of 10 rad(Si)/s.

Fig. 7. Normalized amplitude of 1/f noise, ΔB/B0, versus total dose.

Let

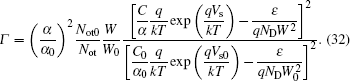
Figure 8 shows the plot of Γ versus oxide-trapped charge density based on Eq. (32). All analytical calculations are carried out by using MATLAB software. The following analytical calculation parameters are used: T = 300 K, q = 1.6 × 10−19 C, ɛSi = 8.85 × 11.9 × 10−14 F/cm, VEB = 0.66 V, ND = 1017 cm−3, NA = 1020 cm−3. It follows from Fig. 8 that Γ first increases and then increases as Not increases.

Fig. 8. Γ as a function of oxide-trapped charge density Not.

The increase of base current noise spectrum SIB with dose augment can be explained as follows. With the accumulation of total dose, the oxide-trapped charges and the interface states increase. Firstly, according to Eq. (25), the induced oxide-trapped charges and interface states can bring about an increase in base surface current, which makes the 1/f noise increase. Secondly, the induced oxide-trapped charges make more carriers participate in the dynamic trapping-detrapping. At the same time, the accumulation forces the width of the space charge region at the surface to decrease, which results in a smaller area at the surface of the space charge region. A smaller area can make the 1/f noise increase. The roles of the oxide-trapped charges are complex. According to Eqs. (31) and (32), the induced oxide-trapped charges can lead to an increase first and then a decrease. However, as oxide-trapped charge density is increased by one order of magnitude, the ΔB/B0 varies (decreases) much less than one order of magnitude. According to Eq. (31), ΔB/B0 is proportional to the interface state density. Combining the contributions made by the oxide-trapped charge and the interface state, we can draw a conclusion that the interface state dominates 1/f noise response. So, 1/f noise would increase with the dose augment.

Many models have been presented to explain ELDRS in a linear bipolar transistor. These models may be grouped into three main categories[35]: 1) space charge models,[36–40] 2) bimolecular process models,[41–46] and 3) a binary reaction rate model.[47] The phenomenon that at the same total dose level ΔI/I0 the ΔB/B0 changes faster at the dose rate of 0.001 Gy(Si)/s than at the dose rate of 0.1 Gy (Si)/s, can be explained with these models. According to these models, more interface states and oxide-trapped charges are induced at the low dose rate, which leads to more severe degradations of the base current and the base 1/f noise at the low dose rate.

4. Conclusions

In this paper, it is suggested that the surface of the space charge region of the emitter-base junction is the main source of the base surface 1/f noise for a PNP bipolar junction transistor with a heavily doped emitter. Based on the theory of carrier number fluctuation and the model of base surface recombination current, a 1/f noise model is developed, which can be used to explain the 1/f noise degradation induced by the radiation. Combining the models of ELDRS, this model can explain the fact that the 1/f noise is more severe at a low dose rate than at a high dose rate. The essential point of this work is to qualitatively describe the radiation-induced 1/f noise degradations of PNP bipolar transistors. Although many important aspects of the problem are neglected, the presented model may be helpful for understanding some of the features of bipolar radiation response.

Reference
1Witczak S CSchrimpf R DGalloway K FFleetwood D MSchrimpf R DPease R LPuhl J MSchmidt D MCombs W ESuehle J S 1996 IEEE Trans. Nucl. Sci. 43 3151
2Petrov A SUlimov V N 2012 Microelectronics Reliability 52 2435
3Schrimpf R D 1996 IEEE Trans. Nucl. Sci. 43 787
4Schmidt D MWu ASchrimpf R DFleetwood D MPease R L 1996 IEEE Trans. Nucl. Sci. 43 3032
5Enlow E WPease R LCombs W ESchrimpf R D 1991 IEEE Trans. Nucl. Sci. 38 1342
6Pease R LSchrimpf R DFleetwood D M 2009 IEEE Trans. Nucl. Sci. 56 1894
7Fleetwood D M 2013 IEEE Trans. Nucl. Sci. 60 1706
8Pease R L 2003 IEEE Trans. Nucl. Sci. 50 539
9Rowsey N LLaw M ESchrimpf R DFleetwood D MTuttle B RPantelides S T 2011 IEEE Trans. Nucl. Sci. 58 2937
10Rashkeev S NCirba C RFleetwood D MSchrimpf R DWitczak S CMichez APantelides S T 2002 IEEE Trans. Nucl. Sci. 49 2650
11Gonzalez-Velo YBoch JSaigné F 2011 IEEE Trans. Nucl. Sci. 58 2953
12Boch JSaigné FSchrimpf R DVaillé J RDusseau LLorf‘evre E 2006 IEEE Trans. Nucl. Sci. 53 3655
13Adell P CEsqueda I SBarbaby H JRax BJohnston A J 2012 IEEE Trans. Nucl. Sci. 59 3081
14Rowsey N LLaw M ESchrimpf R DFleetwood D MTuttle B RPantelides S T 2012 IEEE Trans. Nucl. Sci. 59 3069
15Xi S BLu WRen D YZhou DWen LSun JWu X 2012 Acta Phys. Sin. 61 236103 (in Chinese)
16Xi S BLu WWang Z KRen D YZhou DWen LSun J2012Acta Phys. Sin.61076101(in Chinese)
17Ma W YWang Z KLu WXi S BGuo QHe C FWang XLiu M HJiang K 2014 Acta Phys. Sin. 63 116101 (in Chinese)
18Prince J LStehlin R A 1971 IEEE Trans. Nucl. Sci. 18 404
19Zhao Q FZhuang Y QBao J LHu W 2015 Acta Phys. Sin. 64 136104 (in Chinese)
20Sah C TNoyce R NShockley W 1957 Proc. IRE 45 1228
21Kosier S LSchrimpf R DNowlin R NFleetwood D M 1993 IEEE Trans. Nucl. Sci. 40 1276
22Pershenkov V SMaslov V BCherepko S VShvetzov-Shilovsky I NBelyakov V VSogoyan A VRusanovsky V IUlimov V NEmelianov V VNasibullin V S 1997 IEEE Trans. Nucl. Sci. 44 1840
23Stoisiek MWolf D 1980 IEEE Trans. Electron. Dev. 27 1753
24Van der Ziel AZhang XPawlikiewicz A H 1986 IEEE Trans. Electron. Dev. 33 1371
25Jäntsch O 1987 IEEE Trans. Electron. Dev. 34 1100
26Kleinpenning T G M 1992 IEEE Trans. Electron. Dev. 39 1501
27Kleinpenning T G M 1994 IEEE Trans. Electron. Dev. 41 1981
28Deen M JPascal F 2004 IEEE Proc.-Circuits Devices Syst. 151 125
29Mounib AGhibaudo GBalestra F 1996 J. Appl. Phys. 79 3330
30Zhuang Y QSun Q1993Noise and Its Minimizing Technology in Semiconductor DevicesBeijingNational Defenses Industry Press83 (in Chinese)
31A LMcWhorter A L1957Semiconductor surface physicsPhiladelphiaUniversity of Pennsylrnia Press
32Zhuang Y QSun Q 1991 IEEE Trans. Electron Dev. 38 2540
33Bao J LZhuang Y QDu L2004Chin. J. Sci. Instrum.25335(in Chinese)
34Deen M JRumyantsev S LSchroter M 1999 J. Appl. Phys. 85 1192
35Pease R LSchrimpf R DFleetwood D M 2009 IEEE Trans. Nucl. Sci. 56 1894
36Fleetwood D MKosier S LNowlin R NSchrimpf R DReber R AJrDeLaus MWinokur P SWei ACombs W EPease R L 1994 IEEE Trans. Nucl. Sci. 41 1871
37Fleetwood D MRiewe L CSchwank J RWitczak S CSchrimpf R D 1996 IEEE Trans. Nucl. Sci. 43 2537
38Witczak S CLacoe R CMayer D CFleetwood D MSchrimpf R DGalloway K F 1998 IEEE Trans. Nucl. Sci. 45 2339
39Graves R JCirba C RSchrimpf R DMilanowski R JMichez AFleetwood D MWiczak S CSaigne F 1998 IEEE Trans. Nucl. Sci. 45 2352
40Rashkeev S NCirba C RFleetwood D MSchrimpf R DWitczak S CMichez APantelides S T 2002 IEEE Trans. Nucl. Sci. 49 2650
41Hjalmarson H PPease R LWitczak S CShaneyfelt M RSchwank J REdwards A HHembree C EMattsson T R 2003 IEEE Trans. Nucl. Sci. 50 1901
42Tsetseris LSchrimpf R DFleetwood D MPease R LPantelides S T 2005 IEEE Trans. Nucl. Sci. 52 2265
43Boch JSaigne FTouboul A DDucret SCarlotti J FBernard MSchrimpf R DWrobel FSarrabayrouse G 2006 Appl. Phys. Lett. 88 232113
44Boch JSaigne FSchrimpf R DVaille J RDusseau LLorfevre E 2006 IEEE Trans. Nucl. Sci. 53 3655
45Fleetwood D MSchrimpf R DPantelides S TPease R LDunham G W 2008 IEEE Trans. Nucl. Sci. 55 2986
46Hjalmarson H PPease R LDevine R 2008 IEEE Trans. Nucl. Sci. 55 3009
47Freitag R KBrown D B 1998 IEEE Trans. Nucl. Sci. 45 2649