Cite this Article
Li Min, Li An-Yuan, He Bo-Qu, Yuan Shuai, Zeng He-Ping. Modulation of terahertz generation in dual-color filaments by an external electric field and preformed plasma. Chinese Physics B, 2016, 25(4): 044209  
Permissions
Modulation of terahertz generation in dual-color filaments by an external electric field and preformed plasma
Li Min1, Li An-Yuan1, He Bo-Qu2, Yuan Shuai1, Zeng He-Ping1, 2, †,
Shanghai Key Laboratory of Modern Optical System, Engineering Research Center of Optical Instrument and System (Ministry of Education), School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China

 

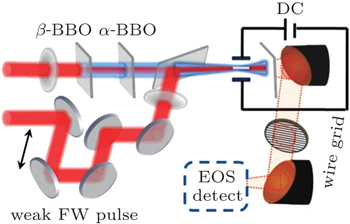
† Corresponding author. E-mail: hpzeng@phy.ecnu.edu.cn

Project supported by the National Key Scientific Instrument Project, China (Grant No. 2012YQ150092), the National Basic Research Program of China (Grant No. 2011CB808105), the National Natural Science Foundation of China (Grant No. 11434005), the China Postdoctoral Science Foundation (Grant No. 2014M560348), and the Fund from the Shanghai Municipal Science and Technology Commission, China (Grant No. 14JC1401600).

Abstract
Abstract

Terahertz generation driven by dual-color filaments in air is demonstrated to be remarkably enhanced by applying an external electric field to the filaments. As terahertz generation is sensitive to the dual-color phase difference, a preformed plasma is verified efficiently in modulating terahertz radiation from linear to elliptical polarization. In the presence of preformed plasma, a dual-color filament generates terahertz pulses of elliptical polarization and the corresponding ellipse rotates regularly with the change of the preformed plasma density. The observed terahertz modulation with the external electric field and the preformed plasma provides a simple way to estimate the plasma density and evaluate the photocurrent dynamics of the dual-color filaments. It provides further experimental evidence of the photo-current model in governing the dual-color filament driven terahertz generation processes.

PACS: 42.65.–k;52.38.–r;42.65.Re;
Keyword:terahertz generation;laser filament;
1. Introduction

In recent years, optimization of the terahertz (THz) generation has received much attention due to its significant applications in imaging, sensing and nonlinear THz spectroscopy.[1] The laser-produced plasma scheme has been a potential and effective method to provide sufficiently powerful far-field THz waves.[2–4] Furthermore, an external electric field has been applied to the single-color filament to enhance the THz intensity. Through this method, a THz electric field parallel to the direction of an external electric field is increased obviously.[5–7] It is well confirmed that THz radiation could be generated from a time-dependent drifting current induced by an asymmetric laser field of dual-color pulse.[8–10] The generated THz intensity and polarization could be modulated by controlling the phase difference and intensities of the dual-color pulses because of its highly nonlinear and phase-sensitive features.[11–16] In this sense, dynamic control of the drifting electrons in the plasma is important for controlling the THz intensity and polarization state. The time- or frequency-characteristics of THz radiation could also be modulated by varying the drifting electrons. This research provides theoretical basis and technical support for precise imaging and spectrum analysis in the THz range.

In this paper, an external dc-biased electric field is used to increase the drifting current by accelerating electrons in the plasma. Compared with the THz radiation driven by a single-color filament, an arbitrary polarization component of the THz radiation is enhanced dramatically with the increase of the external electric field. In addition, the refractive index of air presents a gradient distribution with the existence of preformed plasma. The phase difference between dual-color pulses changes as they pass through the preformed plasma, leading to the elliptically polarized THz radiation. Furthermore, the ellipticity and polarization ellipse are modulated regularly with the cooperation of these two effects. On the other hand, the preformed plasma density could be estimated from the THz polarization state change induced by the preformed plasma.

2. Experimental setup

The experiments were done with a Ti: sapphire amplifier operated at 800 nm with a repetition rate of 1 kHz. The fundamental-wave (FW) pulses with an output pulse energy of 2.3 mJ and a pulse duration of 50 fs were split into two pulses by a 2:1 beam splitter (Fig. 1). The strong FW pulse was focused by a convex lens (f = 60 cm) to create a ∼ 1.5 cm length filament, which was sandwiched by parallel electrodes with 1.4-cm gap. Then a 200-μm-thick β-BBO crystal was inserted behind the lens to generate the dual-color pulse. An x-cut 2.5-mm-thick α-BBO crystal was used to compensate for the phase lag between the FW and the second harmonic (SH) pulses. A weak FW (weak-800 nm) pulse focused by a positive lens (f = 80 cm) was combined collinearly with the dual-color pulse by a Brewster plate. The polarization of the weak-800 nm was perpendicular to the experimental table and it was defined as the s polarization. The polarizations of FW and SH waves were s- and p-polarized (perpendicular and parallel to the experimental table), respectively. The residual laser, after the filament, was blocked by inserting a teflon plate filtering out the THz wave above 3 THz. The electro-optic sampling measurement was employed to detect the generated THz waveform after the filament and the THz polarization had been measured by a wire-grid THz polarizer.

Fig. 1. Experimental setup. THz emission was generated from the dual-color pulses. Parallel electrodes with 1.4-cm spacing are used to provide an external electric field. A weak FW pulse is overlapped with the dual-color pulses, which introduces plasma to control the THz emission.
3. Results

According to the photo-current mode proposed by Kim et al., the drifting electrons accelerated by the asymmetric electric field of the dual-color pulses form a transverse plasma current J⊥ = eNeυe, leading to the THz generation.[17,18] In our experiment, besides the acceleration from the asymmetric electric field, the external electric field also accelerates the drifting electrons. Therefore, the electron velocity υe under the dual-color pulse laser field and external electric field can be expressed as

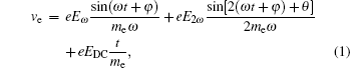
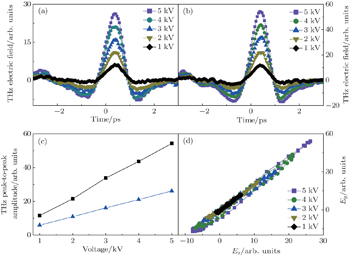
where Eω sin(ωt + φ) and E2ω sin[2(ωt + φ) + θ] are the laser field of the FW and SH pulses, respectively; EDC is the external electric field parallel to the FW pulse polarization; θ is the relative phase between the FW and SH pulses; φ represents the FW pulse phase. As described, the generated THz waveform is determined by the phase difference between the dual-color pulses, the FW and SH intensities, and the external electric field, which influence the drifting electrons.

3.1. Modulation by external electric field

Firstly, an external electric field parallel to the s direction is applied to the dual-color filament in the absence of a weak-800 nm pulse. With no external electric field applied, the drifting electrons are accelerated by two orthogonal laser fields from dual-color pulses. The generated THz radiation is linearly polarized with a fixed angle with respect to the p direction. With an external electric field applied, its electric field contributing to the acceleration of electrons along the s and p directions can be expressed as Ex = EDC sin α cos α and Ey = EDC sin2 α in the x and y directions, respectively, where EDC is the amplitude of the external electric field, α is the angle between the THz polarization and p polarization direction. Therefore, the drifting electrons are both accelerated along the two orthogonal directions, leading to the enhancement of two orthogonal components of THz radiation as shown in Figs. 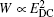2(a) and 2(b). The change of the THz peak-to-peak amplitude with the external electric field is described in Fig. 2(c). Each component of the THz electric fields is linearly proportional to the external electric field. It agrees well with the result reported in Ref. [19], where W represents the total THz energy. As shown by the black curve in Fig. 2(c), along the direction of the external electric field, a strong THz polarization component is generated due to the external field driven acceleration of electrons along the corresponding direction. As a result, two different polarization ellipses originate from different effects on the two THz polarization components. A perfect linearly polarized THz emission is generated and retained as the THz intensity increases with the enhancement of the external electric field as shown in Fig. 2(d). This is attributed to the constant phase difference between the dual-color pulses in the process of applying an external electric field.

Fig. 2. (a) and (b) Variations of THz electric fields in s and p directions as the external electric field increases from 1 kV to 5 kV. (c) Variation of the THz peak-to-peak amplitudes with an external electric field in s and p polarizations. (d) Plots of the THz polarization versus Ex at different external electric fields.
3.2. Modulation by preformed plasma

A pre-formed plasma is generated by a focused weak 800-nm pulse polarized in parallel to the direction of the external electric field, which can be used to influence the dual-color filament. The polarization scenarios of the generated THz are shown in Fig. 3, which is collected with an increasing external electric field and a weak 800-nm pulse energy of 0.47 mJ. Both s and p components of the THz electric field increase with an increase in the external electric field. The generated THz is elliptically polarized rather than linearly polarized in the absence of pre-plasma. In this process, electrons drift out and are accelerated under the asymmetric electric field from the dual-color pulses. Then, the external electric field accelerates the drifting electrons furthermore, leading to the enhancement of generated THz intensity along the two directions. But, the polarization ellipse of the generated THz remains unchanged with the increase of the external electric field. As is well known, the refractive index induced by laser plasma changes according to δnplas ∼ –ρ/2ρcr, where ρ is the electron density of the plasma and ρcr is the critical density closely related to the laser wavelength, i.e., ρcr ∼ λ−2. Therefore, the preformed plasma induces a negative index change and acts as a concave lens for the following pulse passing through it. In addition, the phase difference between the dual-color pulses appears during the passage through the preformed plasma due to υmis = c[1/n(ω)–1/n(2ω)], where υmis is the velocity mismatch of the dual-color pulses, c is the speed of light in a vacuum, n(ω) and n(2ω) are the refractive indexes for FW and SH pulses, respectively. The elliptically polarized THz is generated in the experiment since the dual-color pulses have a phase difference after passing through the pre-formed plasma.

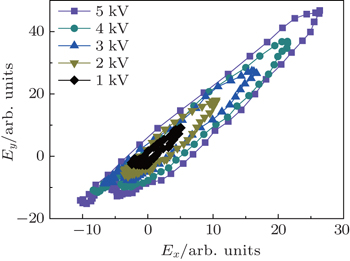Fig. 3. Measured THz polarization states at different external electric fields with 0.47-mJ FW pulse energy.

For the elliptically polarized laser, the polarization ellipse is related to phase difference and the electric field ratio of the orthogonal laser fields. In the experiment, the phase difference between dual-color pulses is constant with a certain plasma density, and the ratio of two orthogonal components keeps constant with the increase of the external electric field. Therefore, the polarization ellipse of generated THz is along the same direction, while the intensity of the generated THz increases with an external electric field at a certain plasma density.

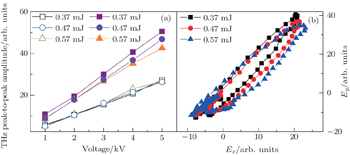
In addition, the THz peak-to-peak amplitudes along the s and p directions are measured as the weak 800-nm pulse energy is adjusted from 0.37 mJ to 0.57 mJ under the condition of a fixed external electric field. The change of the THz peak-to-peak amplitude with the external electric field along the p direction is independent of the weak 800-nm pulse energy. However, as shown in Fig. 4(a), the s component of the THz electric field decreases as the weak 800-nm pulse energy increases. The dispersive effect is strengthened as the plasma density increases with the increase of the weak 800-nm pulse energy, leading to the decrease of the THz electric field. Also, the electron ion collision rate υe is proportional to 1012 s−1, i.e., υe ∼ 1012 s−1, implying that the electron coherent movement is on a picoseconds scale. This movement blocks the drifting electrons from tunneling ionization by dual-color pulses and reduces the radiation of the generated THz. The dispersive and blocking effects become obvious as the plasma density increases with the enhancement of the weak-800 nm energy. Meanwhile, the velocity mismatch of the dual-color pulses also increases due to the dispersive effect, resulting in different phase differences between FW and SH pulses. This further makes the generated THz polarization rotate as shown in Fig. 4(b). The THz polarization rotates clockwise as the weak-800-nm pulse energy changes from 0.37 mJ to 0.57 mJ, which provides an optical method to control the THz polarization. As is well known, the plasma is generated as the energy of the focused laser pulse is higher than the critical pulse energy. In this process, the Kerr self-focusing effect affects the refractive index in about 100 fs, and then the refractive index keeps stable on a picosecond time scale under the influence of plasma. Therefore, the modulation of THz generation induced by preformed plasma can be realized on a femtosecond time scale.

Fig. 4. (a) Plots of measured THz peak-to-peak amplitude versus external electric field for s (hollow circle) and p (solid circle) polarization for the weak 800-nm energies of 0.37, 0.47, and 0.57 mJ, respectively. (b) The THz polarization rotations with the weak 800-nm pulse energies of 0.37, 0.47, and 0.57 mJ, respectively. Here the external electric field is at 5 kV.
4. Conclusions and perspectives

In this paper, we demonstrate that THz generation from dual-color pulse filaments is regularly modulated by an external electric field. The two components of the THz electric field increase with the enhancement of the external electric field. The THz polarization is modulated from linear polarization to an elliptical one. Meanwhile, the rotation of the THz polarization can also be achieved by adjusting the weak-800 nm pulse energy. All the experimental results can be explained well according to the photo-current model, thereby providing an effective method to prove the THz generation mechanism.

Reference
1Ferguson BZhang X C 2002 Nat. Mater. 1 26
2Sherwin M SSchmuttenmaer C ABucksbaum P H2004Report on a DOE-NSF-NIH Workshop
3Hamster HSullivan AGordon SWhite WFalcone R W 1993 Phys. Rev. Lett. 71 2725
4Leemans W PC. Geddes G RFaure JToth CsTilborg JSchroeder C BEsarey EFubiani GAuerbach DMarcelis BCarnahan M AKaindl R AByrd JMartin M C 2003 Phys. Rev. Lett. 91 074802
5Loffler TJacob FRoskos H G 2000 Appl. Phys. Lett. 77 453
6Houard ALiu YPrade BTikhonchuk V TMysyrowicz A 2008 Phys. Rev. Lett. 100 255006
7Sun WZhou YWang XZhang Y2008Opt. Express1616573
8Kress MLöffler TEden SThomson MRoskos H G 2004 Opt. Lett. 29 1120
9Chen YYamaguchi MWang MZhang X C 2007 Appl. Phys. Lett. 91 251116
10Bartel TGaal PReimann KWoerner MElsaesser T 2005 Opt. Lett. 30 2805
11Dudovich NSmirnova OLevesque JMairesse YIvanov M YVilleneuve D MCorkum P B 2006 Nat. Phys. 2 781
12Xie XDai JZhang X C 2006 Phys. Rev. Lett. 96 075005
13Li MLi WShi YLu PZeng H P 2012 Appl. Phys. Lett. 101 161104
14Wu JTong YLi MPan HZeng H P 2010 Phys. Rev. 82 053416
15Li MPan HTong YChen CShi YWu JZeng H P 2011 Opt. Lett. 36 3633
16Dai JKarpowicz NZhang X C 2009 Phys. Rev. Lett. 103 023001
17Cook D JHochstrasser R M 2000 Opt. Lett. 25 1210
18Kim K YGlownia J HTaylor A JRodriguez G 2007 Opt. Express 15 4577
19Chen YWang TMarceau CThéberge FMarc ChâteauneufJacques DuboisOlga KosarevaSee Leang Chin 2009 Appl. Phys. Lett. 95 101101