The saturated absorption spectrum (SAS) is a widely used technique in laser frequency stabilization and atomic physics. In this technique, the laser beam is split into a weak probe beam and a strong pumping beam. These two beams are sent in opposite directions through one vapor cell. Because of the Doppler effects, only the atoms which are in the narrow range of axial velocity centered at v = 0 interact with both light waves and some peaks corresponding to the exact transition between the ground and excited states appear. At the same time, there are also some crossovers when the laser frequency is tuned exactly midway between two transitions if they are close enough. Owing to the saturation effect, the spectra are all peaks on the background of the Doppler-broadened absorption profile in a normal SAS.^[1,2] The normal SAS is very useful for high resolution spectroscopy, but can also be unsatisfactory in other applications. For example, in an optically pumped rubidium beam frequency standard,^[3] the detection laser is stabilized on the transition from F = 2 to F′ = 3 of the ⁸⁷Rb D² resonance line, but there are six peaks at the same time when the SAS method is used. Some groups proposed to shift or eliminate the close crossover peak with two lasers to avoid the influence of these undesired peaks.^[4] However, these six peaks still exist and there is still some possibility of locking the wrong peak. Some SAS peaks can be inverted if the laser intensity is changed or the polarization is tuned. It is called abnormal SAS and some groups have done some theoretical and experimental work.^[4–13]

Considering the similarities and dissimilarities between the normal SAS and abnormal SAS, we subtract the normal SAS and abnormal SAS to obtain a single peak spectrum of ⁸⁷Rb. Obviously, using the single peak spectrum to lock the laser, one can avoid the mis-locking problem. In this paper, the mis-locking mainly means the laser locking of a wrong peak in the SAS. Meanwhile, we ensure that the laser keeps locking by using the digital locking method.

The rest of this paper is organized as follows. In Section 2, we first describe the apparatus of normal SAS and abnormal SAS, then we present the single peak spectrum that subtracts the normal SAS and abnormal SAS. Finally, we show the results of the long-term locking. In Section 3, we set up a theoretical model to explain the abnormal SAS. Conclusions are given in Section 4.

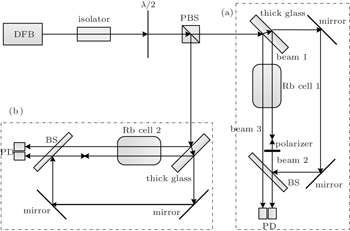
The experimental setup consists of a normal saturated absorption spectrum configuration and an abnormal saturated absorption spectrum configuration shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Experimental schematic diagram. DFB: distributed feedback laser, λ/2: half wave plate, PBS: polarizing beam splitter, BS: beam splitter, Rb: cell the rubidium cell, PD: photodiode. Part (a) is the experimental setup of the abnormal saturated absorption spectroscopy. Part (b) is the experimental setup of the normal saturated absorption spectroscopy.

As shown in part (a) in Fig. 1, a thick glass plate with a reflectivity of ∼ 4% is used to reflect the laser beam and turn it into two parallel reflected beams (beam 1 and beam 3) which transmit through the rubidium cell 1. The transmitted beam from the glass plate is reflected by two mirrors and a beam splitter (reflectivity ∼ 50%) to become beam 2, which acts as a pumping beam. It is collinear with beam 1 which is the probe beam. The probe beam can be detected by a photodiode to obtain the normal SAS. In order to obtain the Doppler-free normal SAS, we put another photodiode to detect beam 3.

As shown in Fig. 1(b), the difference of the abnormal SAS experimental setup from the normal one is the additional polarizer. The additional polarizer can ensure that the pumping beam is linearly polarized and the pumping and probe beam are polarized in the same polarization direction. Compared with the other polarization configurations of the pumping and probe laser beam,^[8,9] the experimental setup of π∥π is rather simple. When the polarization configuration of the pumping and probe laser beam is π∥π, we can obtain the abnormal saturated absorption spectra of the transition 5²S_1/2, F = 2–5²P_3/2, F′ = 3 of the ⁸⁷Rb D₂ line.

We use an Rb cell to measure a cylinder with 20 mm in diameter and 50-mm long at room temperature. The 780-nm laser system is a commercial TOPTICA DL100 laser. The modulation frequency is 5 kHz. It provides a pumping beam power of 3.60 mW and a probe beam power of 0.40 mW for the abnormal SAS setup. Meanwhile, it provides a pumping beam power of 0.37 mW and a probe beam power of 0.06 mW for the normal SAS setup. The spot diameter of the laser beam is about 2 mm.

The experimental normal and abnormal saturated absorption spectra are shown in Fig. 2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Saturated absorption spectra. In this figure, the black line represents the abnormal saturated absorption spectrum and the red line represents the normal saturated absorption spectrum.

The single strong peak can be obtained when the two spectra are subtracted with the help of electronics. The optimal result is shown in Fig. 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Spectrum (black) after subtracting two spectra and being magnified by one operational amplifier, and normal saturated absorption spectrum (red) being the same as that in Fig. 2.

Comparing the two spectra in Fig. 3, we find the target peak is much stronger than the other peaks. The single peak spectrum is an ideal spectrum for laser locking if we can set a certain reasonable threshold intensity. This laser-locking method can avoid the mis-locking phenomenon which often occurs in the normal SAS laser frequency locking system. The error signal of the single peak is obtained and used to control the current of a distributed feedback (DFB) diode laser.

The result is shown in Fig. 4. The laser continuously keeps locking for more than 22 days. In the experiment, we just verified the feasibility of the single peak method. We did not measure the laser locking linewidth, nor frequency drift nor residual frequency fluctuation. In the experiment, the white noise, 1/f noise, PM-to-AM noise and intermodulation noise will all influence the laser locking linewidth. The free-running linewidth of the laser we used is about 2 MHz. In this way, the locking laser linewidth will be larger than 2 MHz because of the intermodulation noise and PM-to-AM noise. The temperature fluctuation of the environment and head generation of the laser diode working will cause the laser frequency to drift. We can roughly estimate the residual frequency fluctuation. The open-loop gain of the P-I servo controller is about 15. The full width at half maximum of the “single peak” from Fig. 3 is about 30 MHz. The linewidth broadening is induced by the strong power of the laser beam. We can estimate the residual frequency fluctuation to be about 2 MHz.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Result of the laser locking. We obtain the photodiode voltage for 22 days. The laser remains in the locking state when the floating range of the photodiode voltage is 100 mV–200 mV. The sampling time of each point is 10 s.

There have been many studies about the formation mechanism of the saturated absorption spectrum.^[5,6] The four-level optical pumping model by Nakayama is a great method for predicting the theoretical saturated absorption spectrum.^[7] Moon and Noh^[8] obtained analytic solutions for the saturated absorption spectrum of ⁸⁷Rb by calculating the rate equation model and the predicted accurate saturated absorption spectrum under all experiment conditions. At the same time, their theory is too complex to explain the abnormal saturated absorption spectrum. In this paper, we simplify Moon and Noh’s theory to study the formation mechanism of the inverse absorption peak on the basis of these studies.

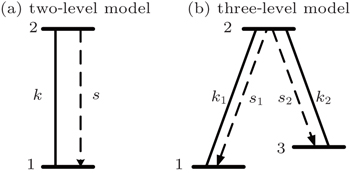
In order to present the theoretical model as clearly as possible, we proceed in two steps: firstly, we describe the modification of the population of ⁸⁷Rb atoms on each level due to the pump laser. Secondly, we analyze the change of the probe laser intensity. We use the rate equation to calculate the modification of the atoms. Before further discussion on the abnormal saturated absorption spectrum, we set up a simple model to explain the formation mechanism of the inverse absorption peak. In the theoretical discussion of this section, we set the laser as ideal monochromatic light unless otherwise stated.

3.1. Simple model

Firstly, we consider the two-level model which is shown in Fig. 5(a). There will not be an optical pumping effect in the two-level model due to its simple structure, so an inverse absorption peak does not arise.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Level system for the simple model. The two-level model (a) and three-level model (b) are shown. In the figure k, k1, and k2 are stimulated emission rates, s, s1, and s2 are spontaneous emission coefficients.

We list two rate equations of the three-level model, where equation (1) does not take the spontaneous emission into consideration, while equation (2) does.

where n₁ and n₃ denote the ground-state populations, and n₂ denotes the excited-state population. The a and t denote the coefficients related to the pump light intensity and time respectively.

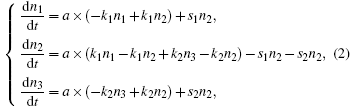
Then, we consider the three-level model shown in Fig. 5(b). In the conventional calculation, we need to consider the stimulated emission and spontaneous emission. However, the necessity of spontaneous emission is still to be discussed.

We calculate Eqs. (1) and (2) with the fourth order Runge–Kutta method in Matlab in which the accuracy is 10⁻⁶. The result is shown in Figs. 6(a) and 6(b). From these figures, we see that the optical pumping effect occurs when spontaneous emission is taken into account. Then we calculate the modification of the probe laser. The atoms can absorb the probe laser and thus the atoms in the ground-state are excited to the excited-state. So we obtain the modification of the probe laser intensity by ignoring the fluorescence from the excited-state

where b and I₀ denote the coefficients related to the probe light intensity and probe light intensity, respectively.

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. Theoretical simulation results. Panels (a) and (b) show the modification of the 87Rb atoms, panels (c) and (d) show the modification of the probe laser. In panels (a) and (b), the black line represents n1, the red line denotes n2, and the blue line refers to n3. In these panels, the t, N, I, I0, and N0 denote the time, modification of the number of atoms, modification of the probe laser intensity, probe laser intensity, and the number of atoms. The P1 and P2 are the points we select from panels (c) and (d), where the a = 1, b = 1, I0 = 1, k1 = 0.001, k2 = 0.005, s1 = 0.01, s2 = 0.05, n1 = n2 = 1/2, and n2 = 0.

We calculate the modification of the probe laser intensity by using Eq. (3). Figure 6(c) shows the modification without the spontaneous emission. Figure 6(d) shows the modification with spontaneous emission. Comparing the two figures, we obtain the different modifications of the slope of the curve. To confirm the necessity of spontaneous emission, we select two points P₁ and P₂. We set the slopes of P₁ and P₂ as S₁ and S₂ respectively. In the following, we consider the lineshape of the probe laser to explain the formation of the inverse absorption peak. If we only consider the natural linewidth and ignore the Doppler broadening effect, the laser intensity a as shown in Fig. 6 is defined as

where g(Δv), A, Δv_N, and Δv denote the natural absorption lineshape, the coefficient related to the light intensity, the natural linewidth, and the relative frequency difference. The lineshapes of the probe signal as shown in Figs. 6(c) and 6(d) can be defined as

where the I_probe denotes the lineshape of the probe laser. In this section, we consider the whole model in a state of resonance. So t is a constant which can be ignored in practice. The lineshape of the probe laser will be

With a simplified equation, we only analyze the slopes of the curve near the P₁ and P₂. In this case, equation (6) becomes

where S denotes S₁ or S₂, when S = S₁, equation (7) does not consider the spontaneous emission, and when S = S₂, equation (7) takes into consideration the spontaneous emission. The S₁ is positive but the S₂ is negative. So the lineshape of the probe laser considering the spontaneous emission is an inverse absorption peak from Eq. (7). This means that the spontaneous emission is a necessary condition of the inverse absorption peak. In addition, the appropriate interaction time and laser intensity are also calculated.

3.2. ⁸⁷Rb atom model

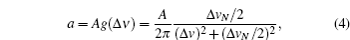
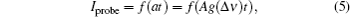
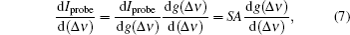
In the above subsection, the formation of the inverse absorption peak has been analyzed by setting up a simple model. In this subsection, we will calculate the saturated absorption spectrum of ⁸⁷Rb.

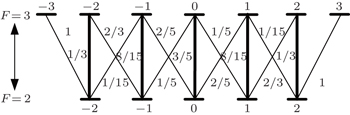
In the experiment, we obtain the normal and abnormal saturated absorption spectrum of the transition 5²S_1/2, F = 2–5²P_3/2, F′ = 3 of the ⁸⁷Rb with one DFB laser (780 nm) simultaneously. The abnormal saturated absorption spectrum is created by using the probe and pumping laser beam of π-polarization. As is shown in Fig. 7, we list the rate equation of the ⁸⁷Rb as

where the i, a, k_ij, and s_ij denote the number of levels, coefficient related to the pumping light intensity, stimulated emission coefficient, and spontaneous emission coefficient. On the right-hand side of Eq. (8), the first item represents the energy level transition by the laser transition, the second item denotes the energy level transition by stimulated emission, and the third item refers to the energy level transition by spontaneous emissions.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Normalized transition probabilities between all magnetic sublevels in the transition 52S1/2, F = 2–52P3/2, F′ = 3 of the 87Rb D2 resonance line. The numbers near the line are the transition probabilities between the ground-state and the excited-state. The bold line represents the transition line which uses the π-polarization laser.

The modification of the probe laser intensity is defined as

where b denotes the coefficient related to the probe light intensity. In the bracket, the first item represents the absorption in the ground-state, and the second item refers to the emission in the excited-state.

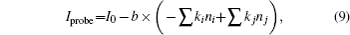
By combining Eq. (8) and Eq. (9), we calculate the modification of the probe laser intensity as shown in Fig. 8. The slope of the line is negative when at > 300. This is why we use the large light intensity of the pumping light in the experiment. Using the method described in Eq. (7), we can calculate the absorption peak in the transition 5²S_1/2, F = 2–5²P_3/2, F′ = 3 of the ⁸⁷Rb D₂ resonance line, which is an inverse absorption peak.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Modification of the probe laser intensity in the transition 52S1/2, F = 2–52P3/2, F′ = 3 of the 87Rb. The I, I0, t denote the modifications of the probe laser intensity, probe laser intensity, and time.

We calculate the other transition of the ⁸⁷Rb D₂ resonance line, which uses the π-polarization laser with the same method as the above. Our calculation indicates that the inverse absorption peak is only feasible in the transitions 5²S_1/2, F = 2–5²P_3/2, F′ = 3 and 5²S_1/2, F = 1–5²P_3/2, F′ = C0,1 of the ⁸⁷Rb D₂ resonance line when the π-polarization light is used. We are also able to calculate the results under various conditions of laser polarization in the same way. The results are shown in Table 1.

Table 1.

Table 1.

Table 1. Absorption peak condition under various laser polarizations. . Polarizationa 2-3b 1-C0, 2 1-1 1-C0, 1 1-0 Ref. π∥π Rc – d – R – [8], [9] σ+–σ+ R R – – – [8], [9] σ+–σ− – – R R R [8], [9] π–σ – – R – R σ–π – – R – R a polarization configurations of the pumping and probe laser beam, b 52S1/2 F = 2−52P3/2 F′ =3 transitions of the 87Rb D2 resonance line, c reversed peak, d normal peak.

Table 1. Absorption peak condition under various laser polarizations. .

In the experiment, we observe the abnormal saturated absorption spectra of the transitions 5²S_1/2, F = 2–5²P_3/2, F′ = 3 of the ⁸⁷Rb D₂ line and obtain the single peak corresponding to the phenomenon to lock the DFB diode laser. We analyze the conditions of the abnormal saturated absorption spectrum and set up a simple theoretical model to explain it. This demonstration opens new possibilities for the laser frequency locking methods.