As is well known, in the past few decades, the nonlinear phenomenon has received a great amount of attention. In particular, the soliton has aroused considerable interest ever since its introduction by Benzi et al. in 1981.^[1] The soliton can be viewed as representing a balance between the effect of nonlinearity and that of dispersion.^[2] In other words, this phenomenon can be found to result from the dynamic interaction between nonlinearity and dissipation. In Ref. [3], the generation of a hole soliton was discussed. Based on the nonlinear Schrödinger equation, the envelope and hole solitons have been also studied well.^[4] In recent years, the gap soliton has been progressively reported in a broad variety of nonlinear systems which have periodic structures.^[5–9] By means of nonlinear supratransmission,^[10,11] Geniet and Leon have investigated the local structure inside the forbidden band, and have given the concept of the cutoff soliton. In addition, the interaction between two solitary waves has been studied in Hertzian chains,^[12] and a family of exact solutions describing discrete solitary waves have been presented^[13] in a nonintegrable Fermi–Pasta–Ulam (FPU) chain. By using the electromagnetically induced transparency effect which produced high dispersion and nonlinearity, Du et al. have investigated the formation environment and the evolution of the dark soliton with environment parameters.^[14] For cases below and above the critical value, bright and dark soliton states admitted by the magnon density distribution have been studied respectively, and the two-soliton collision properties that are modulated by the current have also been discussed.^[15] As one of the nonlinear phenomena, the modulational instability has been investigated.^[16,17] It can be viewed as the interaction between the nonlinear effect and the dispersive effect. In Ref. [16], the envelope soliton can be induced by the modulational instability that leads to a self induced modulation.

The nonlinear phenomenon has been studied in diverse fields, such as nonlinear optics, fluid dynamics, plasma physics, and the electrical transmission line. Indeed, as a convenient tool, the nonlinear LC transmission line (LCTL), which has N cells consisting of inductors L and nonlinear capacitors C, plays a key role in the research of nonlinear wave propagation. Since the pioneering work by Hirota and Suzuki^[18] on a simulation line of the Toda lattice,^[19] it has received a great amount of attention in the nonlinear excitation behaviour investigations. In particular, it provides a useful way to study how the wave propagates in a nonlinear dispersive medium and to model the exotic properties of other new systems.^[2,20,21] For example, the transmission line can be reduced to the nonlinear Schrödinger model.^[22] As the Frenkel–Kontorova and the FPU models are used to investigate the thermal asymmetric energy flux,^[23–29] the LCTLs have been used for modulation instability and the gap soliton,^[7,9,16,22] and great progress has been achieved.

In view of the soliton investigation with the driving frequency above the cutoff, quite a natural question then arises whether the soliton wave would still occur when the driving frequency is chosen in the pass-band. Indeed, while the linear wave is propagating in the system, the modulational instability would be generated by the nonlinearity and dispersion, and then the self modulation (SM) would be induced. In an optical system, the SM and the soliton excitation have been studied.^[30] In this paper, we will choose the appropriate driving amplitude and frequency, and numerically investigate this interesting phenomenon in the LCTL. The outline of the paper is as follows. In Section 2, we will present the model first, which is, in fact, a nonlinear LCTL consisting of many identical cells. In Section 3, we numerically investigate the soliton excitation on the nonlinear electrical network. The dependence of the subharmonic power spectrum and frequency on forcing parameters will be discussed in Section 4. Finally, Section 5 is devoted to some concluding remarks.

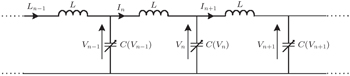
The system under consideration is a lossless nonlinear discrete LCTL which is comprised of many elementary cells as shown in Fig. 1. Each cell consists of an inductor L in the series branch and a capacitor C(V) in the parallel branch. This model has already been used extensively to investigate the cutoff soliton^[22] and the asymmetric energy flux phenomenon^[28,29] both theoretically and experimentally. V_n represents the voltage across the n-th capacitor, while I_n denotes the current through the inductor L of the n-th cell with the subscript n designating the cell number in the network. In the following analysis, we assume that the characteristic of each cell between the capacitance C(V_n) and voltage V_n is described by^[2]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic representation of the lossless LCTL where each cell consists of a linear inductor L and a nonlinear capacitor C(V), and all cells have the same structure and parameters. The In and Vn denote the current flowing through the inductor and the reverse voltage applied to the capacitor, respectively.

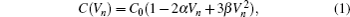
Applying the Kirchhoff’s laws and the capacitance–voltage relationship represented by Eq. (1) to the lossless nonlinear discrete LCTL, we can establish the following equation governing the voltage V(n) propagation:

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Linear dispersion curve of the LCTL. The driving frequency is chosen in the (green) shade area which satisfies the relation P(ω) × Q(ω) > 0 with P(ω) and Q(ω) being the dispersion coefficient and the nonlinear coefficient, respectively. fc and fs are the upper and lower boundary frequencies of the (green) shade domain (fc is also the cutoff frequency of system).

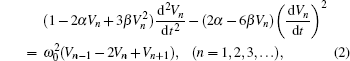
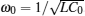
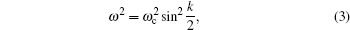
In the study, in order to generate the soliton wave, the f_s is the lower frequency which can be chosen by the driving one, and the magnitude of f_s is 1.0403 MHz. Namely, the driving frequency satisfies

In Refs. [16] and [22], the dispersion curve (see Fig. 2) has already been studied, which focused on the modulational instability, and the dispersion coefficient P(ω) and nonlinear coefficient Q(ω) have also been obtained as

In the whole area, the P(ω) is always negative, whereas the Q(ω) can be positive or negative, depending on the carrier wave frequency ω. In our study, the green region selected in Fig. 2 always satisfies the relationship P(ω) × Q(ω) > 0, where the instability can occur. This is the main reason for choosing the driving frequency in the range (f_s, f_c).

In fact, in the study, the LCTL has the length N which is long enough to avoid the free end reflections, so that the soliton wave can well keep its propagation. Of course, the wave propagation of the internal cells still obeys Eq. (2). We submit the left endpoint of the LCTL into an external constant amplitude periodic driving and have

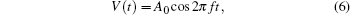
In this section, in order to generate the soliton wave, we perform the numerical simulations on the LCTL [Eq. (2)]. The sinusoidal driving voltage, [Eq. (6)], is submitted to the left end of the LCTL, so that we can verify whether or not the soliton can be generated.

The values of L, C₀, α, and β have been given in Section 2. The frequency and amplitude of the driving voltage are f = 1.1990 MHz and A₀ = 0.3 V, respectively. Obviously, the driving frequency value is located in the pass band (see the green area in Fig. 2). The propagation equation (2) is integrated by the fourth order Runge–Kutta algorithm with a time span Δt = 1/(200f_c). To avoid initial shock, the driving amplitude A₀ is fed into the LCTL smoothly. The numerical simulation is carried out for a sufficiently long time (for example, t = 10 ms).

Figure 3 shows the spatial state of the LCTL at the end of the simulation time. We can see that the energy propagates by means of the generation of localized structures (soliton waves). The wave amplitude can exceed that of the driving voltage during the localization. In other words, while the wave is propagating, the amplitudes of some cells can be larger than the initial driving amplitude A₀ (see red line in Fig. 3), and the maximum amplitude is about 0.7 V in our simulation, namely, V_max ≈ 2.3A₀. The result shows that the wave localization can generate the amplification effect.^[22]

Fig. 3.

	Figure Option ViewDownloadNew Window
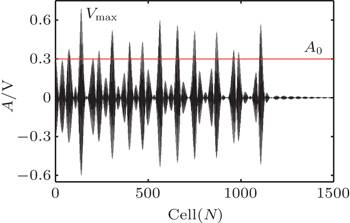	Fig. 3. Final state of the LCTL at the end of simulation for a driving frequency f = 1.1990 MHz and amplitude A0 = 0.3 V. The (red) horizontal line denotes the driving amplitude value A0.

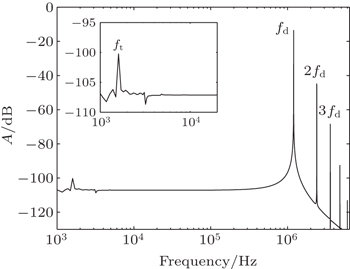
Here, we also calculate the frequency spectrum of a 100-th cell wave by using the fast Fourier transform algorithm (FFT) as shown in Fig. 4. In this paper, unless otherwise stated, the spectrum calculating point is not changed. Obviously, a very low subharmonic component (SH) f_t is generated (see the inset of Fig. 4). Besides, the spectrum consists of the fundamental component f_d whose value equals the driving frequency and its superharmonics (denoted by 2f_d and 3f_d) as well. The subharmonic frequency f_t obtained from Fig. 4 is about 1.598 kHz, which is much lower than the driving one f_d = 1.1990 MHz. This phenomenon shows that the slow modulation of the solitary wave oscillation occurs as shown in Fig. 5. If the LCTL has no nonlinear characteristics, the simulation results show that the modulation will disappear. So, it is recognized that the modulation is induced by the nonlinear effect. While the sine wave propagates in the LCTL, the effect of nonlinearity is to create harmonic components. Then, the sine wave is slowly modulated. The SM of the wave is as shown in Fig. 5. As time goes on and the wave travels along the system, the modulation increases and the continuous wave breaks into the pulse trains for the modulational instability. When the balance between the effect of dispersion and that of nonlinearity is reached, the soliton is formed from the pulse train ultimately.^[30] The modulation is found to vary with the driving frequency f and amplitude A₀. That is to say, the different driving parameters can affect the modulation degree associated with the soliton wave generation. When the f is close to f_s or/and the A₀ is quite small, the modulation becomes weak and the soliton wave is not easy to generate. Conversely, as f is increased or/and the A₀ is increased, the amplitude of the spectral line will increase, and the SH component f_t will also increase. Meanwhile, in the FFT spectrum, there emerges another SH component at f_h possibly, in addition to the subharmonic frequency f_t. Figure 6 shows the spectrum plot for f = 1.1990 MHz and A₀ = 0.60 V. From the plot, we can read that f_t and f_h are about 4.10 kHz and 8.201 kHz, respectively. To generate a soliton wave, however, the driving amplitude is not increased unlimitedly. For example, when the driving frequency is set to be 1.1990 MHz, and the amplitude A₀ is larger than 0.90 V, the chaos will replace the soliton wave.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Plot of frequency spectrum versus frequency of the 100-th cell wave. The fd represents the driving frequency, and the ft denotes the subharmonic frequency. The inset shows the magnified portion in the lower frequency range from 1 kHz to 20 kHz. The calculating conditions are f = 1.1990 MHz and A0 = 0.30 V.

Fig. 5.

	Figure Option ViewDownloadNew Window
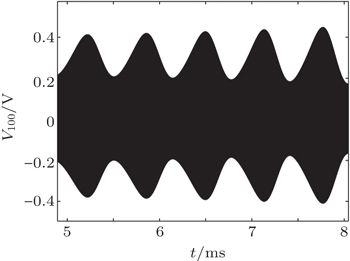	Fig. 5. Time response of the 100-th cell. The driving frequency and amplitude are f = 1.1990 MHz and A0 = 0.30 V, respectively.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The FFT power spectrum calculated at the 100-th cell. The driving frequency and amplitude are f = 1.1990 MHz and A0 = 0.60 V, respectively. The fd represents the fundamental frequency, while the ft and fh denote the subharmonic frequencies.

In this section, we turn our attention to the dependence of SH on the driving parameters f and A₀. By investigation, the modulation is found to vary with f and A₀. That is to say, the modulation will become strong with the driving frequency f or (and) amplitude A₀ increasing. In the spectrum, we can also clearly find the SH component. As a result of the process of the f or/and A₀ increasing, there emerges a second SH f_h coexisting with the first one f_t. Meanwhile, the SH frequency and power would change correspondingly.

Figure 7 shows the relations between the driving amplitude A₀ and the SH frequencies as the driving frequency f is set to be 1.1990 MHz. We observe that the values of the f_t and f_h vary with the change in the driving amplitude A₀. For A₀ ≤ 0.30 V, there is only one SH component f_t, and f_t will completely depress with a gradual decrease of A₀. However, when the A₀ is chosen to be in a range from 0.31 to 0.70 V, the second SH component f_h would emerge, and as the A₀ increases, f_t and f_h values also increase.

Fig. 7.

	Figure Option ViewDownloadNew Window
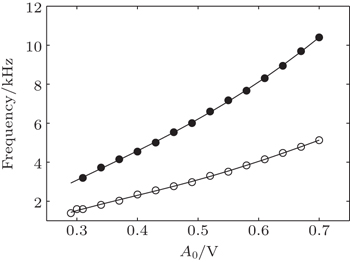	Fig. 7. Plots of subharmonic frequency versus the driving amplitude A0 at the fixed driving frequency 1.1990 MHz. The empty and solid circles represent the frequencies for ft and fh, respectively.

The variations of SH amplitude A with driving amplitude A₀ are calculated and shown in Fig. 8. We can clearly see how the heights of the spectral lines, f_t and f_h, depend on driving amplitude A₀ at the fixed frequency f = 1.1990 MHz. The empty and solid triangles in the figure represent the numerical data of the f_t and f_h, respectively. The full lines are the fitting curves of the numerical data. It can be observed that the amplitude of the f_t line grows rapidly with A₀ changing from 0.29 V to 0.60 V. However, for 0.60 V < A₀ ≤ 0.70 V, the f_t amplitude increases slowly. The f_t amplitude variation means that the strength of the temporal modulation becomes more and more strong with A₀ increasing. The f_h component amplitude obeys the monotonically increasing trend similar to that of the f_t component amplitude, except that the f_h spectral line disappears completely in a range A₀ < 0.30 V. As a matter of fact, we find the modulation strength becomes more and more weak in a range A₀ < 0.29 V, so that all the SH amplitudes cannot be measured effectively.

Fig. 8.

	Figure Option ViewDownloadNew Window
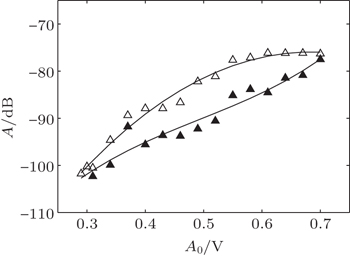	Fig. 8. Plots of subharmonic amplitude A versus driving amplitude A0 at the fixed driving frequency 1.1990 MHz. The empty and solid triangles represent the amplitudes for ft and fh, respectively.

Figure 9 describes the frequencies of f_t and f_h subharmonics against the driving frequency f at the fixed A₀ = 0.70 V. It can be seen that f_t and f_h grow progressively with driving frequency varying from 1.1600 MHz to 1.1950 MHz. When the f value satisfies f < 1.1600 MHz, the spectrum plot only has the f_t component, and with the f value decreasing gradually, the f_t will disappear. For 1.1600 MHz ≤ f ≤ 1.1800 MHz, f_t frequency increases slowly when f increases. However, in the range 1.1800 MHz < f ≤ 1.1950 MHz, f_t undergoes the first decline in the rising process in which the lowest point corresponds to f = 1.1900 MHz.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Variations of subharmonic frequency with driving frequency f at the fixed driving amplitude 0.7 V. The empty and solid circles represent the amplitudes for ft and fh, respectively.

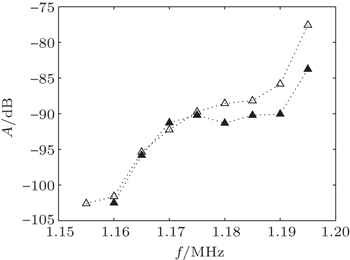
The relation between subharmonic amplitude A and the driving frequency f is plotted in Fig. 10. The data are calculated at A₀ = 0.70 V. From the curves, we can see that f_t and f_h amplitudes both have monotonically increasing trends. For f < 1.1750 MHz, the f_t and f_h amplitudes grow rapidly. In the range 1.1750 MHz≤ f ≤ 1.1900 MHz, the f_t and f_h spectral lines both grow slowly.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. The relation between the subharmonic amplitude A and the driving frequency f at a fixed driving amplitude of 0.7 V. The empty and filled triangles represent the amplitudes for ft and fh, respectively.

From the above, it is easy to understand the soliton wave generation in the LCTL if we consider the nonlinear and modulation effect. Obviously, from Eq. (1), we can see that the nonlinear effect is related to both the driving voltage amplitude and the nonlinear coefficient α. On the other hand, the nonlinear coefficient Q(ω) of the nonlinear Schrödinger equation is closely related to parameter α,^[16,22] namely, the variation of the α value can change the product P(ω) × Q(ω). In the whole analysis, the driving frequency is chosen in the special area (see the green domain of Fig. 2) in which the inequality P(ω) × Q(ω) > 0 holds true, so the dependence of the subharmonic on α is not discussed.

We know that the higher the driving amplitude, the stronger the nonlinear effect is. When the linear wave propagates in the LCTL, the result is that the modulation is induced by the nonlinearity. The numerical data illustrate that the modulation would be enhanced by increasing the driving frequency or/and amplitude. The subharmonic components are closely related to both the driving frequency and the driving amplitude. In the system, the nonlinear effect leads to the generation of subharmonics. From the spectrum, the simulation results show that the subharmonic amplitude is dependent on the driving amplitude A₀. It indicates that the amplitude of the subharmonic will increase with an increase in the nonlinear effect.

In this work, we numerically investigate the generation of soliton waves in the simple LCTL consisting of many cells, and all the cells have the same structure and the same parameters. We can clearly see that the soliton wave can be generated in the pass band based on the SM. When the driving wave propagates in the LCTL, the SM will be induced by the nonlinear effect. This mechanism of the soliton wave generation is completely different from the one which depends on the supratransmission in the forbidden band.^[22,29] As a matter of fact, the choosing of the driving frequency is very important for the soliton wave generation. While the driving frequency is located in the special region of the linear dispersion curve (see the green area of Fig. 2), the modulation instability would be induced. As a result, the SM will also happen. In this study, we find that the modulation instability occurs more easily when the driving frequency is closer to the cutoff frequency f_c, and the SM will also become more and more obvious. The increase in driving amplitude, at a fixed driving frequency satisfying P(ω)×Q(ω) > 0, can also lead to a similar phenomenon. From the spectrum, we can obviously see that the SH components coexist with the fundamental one f_d. By continuously increasing A₀, the soliton wave will disappear, and be replaced by the chaos wave. We numerically investigate the dependences of the subharmonic frequency and power on the driving amplitude as well, and we find that the subharmonic frequency and power would change when the driving amplitude varies. The present numerical simulation of the generation of the soliton wave is conducted in the ideal LCTL, and the experimental investigation of this interesting work is underway, and will be reported in the future.