High-temperature Raman spectroscopic study of vanadoborate Na<bold>3</bold>VO<bold>2</bold>B<bold>6</bold>O<bold>11</bold>

Cite this Article

Zhang Ji, Zhang De-Ming, Zhang Qing-Li, Yin Shao-Tang. High-temperature Raman spectroscopic study of vanadoborate Na₃VO₂B₆O₁₁. Chinese Physics B, 2016, 25(3): 037802 Copy to clipboard

Permissions

High-temperature Raman spectroscopic study of vanadoborate Na₃VO₂B₆O₁₁

Zhang Ji^{1, †,}, Zhang De-Ming², Zhang Qing-Li², Yin Shao-Tang²

1An Hui Xin Hua University, Hefei 230088, China

2Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China

† Corresponding author. E-mail: 18956063545@189.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 51302268 and 51102239) and the Natural Science Foundation of Anhui Province, China (Grant No. KJ2015A339).

Abstract

Raman spectra of a vanadoborate (Na₃VO₂B₆O₁₁) crystal from room temperature up to the melting point have been recorded. The main internal vibrational modes of the crystal have been assigned. It was found that all the Raman bands exhibit decreases in frequency and the widths of the Raman bands increase with the increase of temperature. However, no phase transition was observed under 525 °C. The micro-structure of its melt was studied by quantum chemistry ab initio calculation. The continuous three-dimensional network of the crystal collapsed and transformed into VO₄ and VBO₆ clusters during the melting process with an isomerization reaction from four-coordinated boron to a three-coordinated species.

PACS: 78.30.–j;81.70.–q;63.70.+h

Keyword:Na₃VO₂B₆O₁₁ crystal;high-temperature Raman spectroscopy;vibration mode

Show Figures

1. Introduction

Na₃VO₂B₆O₁₁ (NVBO) is a new nonlinear optical crystal as a result of the investigation of vanadoborate systems. In the past years, Na₂B₄O₇–V₂O₅,^[1] NaBO₂–V₂O₅,^[2] and H₃BO₃–NaVO₃–HNO₃–H₂O^[3] systems have been studied. More recently, Touboul et al.^[4] further investigated the Na₂CO₃–H₂O–V₂O₅–H₃BO₃ system to obtain vanadoborate compound Na₃VO₂B₆O₁₁ first. Then the NVBO crystal has been grown by the top-seeded solution growth method using Na₂CO₃–V₂O₅ flux.^[5] It has a wide transparency range from 370 nm to 3000 nm with the shortest second harmonic generation (SHG) wavelength at 427 nm, which demonstrates that it has potential as optical SHG crystals for blue wavelength applications.

The investigation of the structure of NVBO crystal by x-ray diffraction techniques shows that the compound is orthorhombic, space group P2₁2₁2₁,^[4,5] with cell parameters a = 7.7359 Å, b = 10.1884 Å, c = 12.5697 Å, V = 990.7 Å, and Z = 4. It has a three-dimensional structure consisting of hexaborate groups connected by VO₄ tetrahedra with the sodium atoms distributed in channels throughout the three-dimensional network. Such a hexaborate group made up of a tetrahedron and triangle by sharing one oxygen may form compact atom groups which have been described in several borates, such as Li₂B₄O₇,^[6] CsLiB₆O₁₀,^[7] and LiB₃O₅^[8] crystals. However, the structural stabilization at high temperature is important to the NLO crystal as an optical device. Temperature-dependent Raman scattering measurements are well suited to obtain the structural information of the sample at different temperatures because of the dependence of the phonon modes on temperature.^[9,10] Furthermore, it is essential to investigate the micro-structure of both its crystal and molten phases for being able to achieve large-sized single crystals grown from the melt.^[11] To the best of our knowledge, no studies on Raman scattering about the NVBO crystals have been reported until now, which contribute to a progressive understanding of the crystal structure^[12] as well as more specific aspects of lattice dynamics.^[13] Therefore, in this paper, we recorded the Raman spectra of NVBO single crystal from room temperature to melting point, and the calculation was carried out using quantum chemistry ab initio calculation to study the micro-structure of the solution.

2. Experiment

The NVBO single crystal used in this study was grown by the flux method in Na₂CO₃–V₂O₅ flux system described by Fan et al.^[5] Then the crystal was cut into slices with 2-mm thickness. The room- and high-temperature measurements were carried out using a home-made heating furnace. The temperature was monitored by a thermocouple attached to the metal sample holder and controlled by a temperature controller within 1 °C. The Raman spectra were collected with Horiba Jobin Y’von Raman spectrometer (LabRam800HR) with a backscattering configuration. The ultraviolet light pulse of 355 nm with a repetition frequency of 10 kHz from a coherent Innova ultra laser was focused onto the sample using a Raman microprobe with a 4× objective lens. An intensified charge coupled device (CCD) was used to collect the scattering light. The sample was steadily heated from room temperature to melting point in a platinum boat which was placed in the center of the chamber. The spectral acquisition, under the accumulated mode, was 10 s each time, the average power of the laser operation was fixed at 800 mW and the slit width was set as 300 nm for all the measurements under different temperatures.

3. Results and discussion

3.1. Structures and factor group analyses

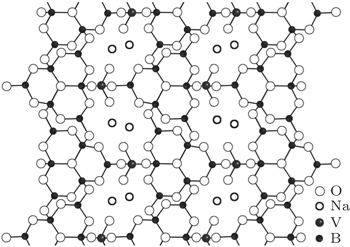
The orthorhombic unit cell of the Na₃VO₂B₆O₁₁ crystal contains four formula units and belongs to the space groups P2₁2₁2₁. According to the research of Touboul,^[4] two groups of atoms can be marked out in the structure of this compound: VO₄ and B₆O₁₃ groups which share common oxygen atoms to form a three-dimensional framework, as shown in Fig. 1. The complex B₆O₁₃ groups contain three non-planar six-member rings (which consist of one BO₃ triangle and two BO₄ tetrahedra, the mean values for B–O bonds are 1.367 Å and 1.469 Å, respectively, sharing with one oxygen. All atoms occupy Wyckoff positions of C₁ site symmetry. The main characteristic of the structure is that it contains [VO₄] (Td) tetrahedra and complex B₆O₁₃ groups with three boron-oxygen rings. Furthermore, one of the rings is formed by one BO₃ (D_3h) triangle and two BO₄ (Td) tetrahedra. The full vibrational representation Γ according to the irreducible representations of C_2v for Na₃VO₂B₆O₁₁ contains 69A₁+69A₂+69B₁+69B₂ modes. A₁+B₁+B₂ are acoustical modes and 68A₁+69A₂+68B₁+68B₂ are optical modes. All of these modes are Raman active.

	Figure Option View Download New Window
	Fig. 1. Projection of structure of Na₃VO₂B₆O₁₁ crystal in the (001) plane.

3.2. Raman spectrum at room temperature

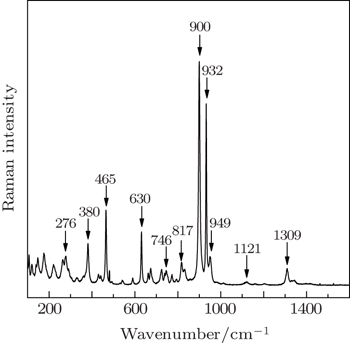
The Raman spectrum at room temperature (300 K) is illustrated in Fig. 2. The assignment of the internal vibrational modes in NVBO is rendered difficult by the structure complexity. A significant contribution to the Raman spectra of NVBO comes from the vibration of a low-symmetric polyborate B₆O₁₃ group consisting of three boroxygen rings and each ring contains one BO₃ triangle and two BO₄ tetrahedra. However, these groups are not independent of each other in the crystal, so the vibrational modes will be assigned according to the vibration modes of BO₃ and BO₄ groups in their free ion state and some similarities with other borate compounds such as Li₂B₄O₇, CsLiB₆O₁₀, and LiB₃O₅ crystals.

	Figure Option View Download New Window
	Fig. 2. Raman spectrum of Na₃VO₂B₆O₁₁ crystal at room temperature.

A planar equilateral triangle molecule BO₃ with D_3h symmetry in its free ion state has four normal vibrational modes. These normal modes are non-degenerate symmetric B–O stretching vibration (v_s), non-degenerate out-of-plane B–O bending vibration (δ), doubly degenerate B–O stretching vibration (v_as) and doubly degenerate in-plane O–B–O bending vibration (γ). It is known that the normal mode frequencies of the BO₃ group in the vibrational spectra of the bismuth borate crystals are typically situated as follows:^[14] v_s∼ 900–1000 cm⁻¹, δ ∼ 650–800 cm⁻¹, v_as∼ 1250–1450 cm⁻¹, and γ ∼ 590–680 cm⁻¹. Elbelrhiti et al.^[15] reported the Raman spectra of Li₂B₄O₇ crystal which contains a basic building block of two BO₄ tetrahedra linked by a common oxygen atom, forming a B₂O₇ group joining two planar triangles BO₃ using the common oxygen atoms. The Raman peaks at 976 cm⁻¹ and 968 cm⁻¹ are observed and assigned to symmetric stretch vibration of BO₃ in the spectra of Li₂B₄O₇ crystal. The 762 cm⁻¹ and 739 cm⁻¹ peaks are related to the BO₃ symmetric deformation, 1447 cm⁻¹ peaks to BO₃ asymmetric stretch. These arguments make the following tentative assignments possible: the strong Raman peak located at 1309 cm⁻¹ is due to v_as vibration of B–O bonds in BO₃ groups; the strong peak located at 932 cm⁻¹ is related to the v_s mode; and the peak at 773 cm⁻¹ due to the non-degenerate B–O bending vibration mode (δ). Finally, the Raman peak located at 630 cm⁻¹ is assigned to the O–B–O bending vibration (γ) in BO₃ triangles, as listed in Table 1.

Table 1.

Raman shift and assignment for the Na₃VO₂B₆O₁₁ crystal at room temperature.

In addition, the BO₃ triangles are connected with BO₄ tetrahedra by B–Ø–B bonds (Ø = bridge oxygen) to form boroxol rings. Such a group with six-numbered B–O rings has been described in several borates. According to Refs. [16] and [17], the nonplanar boroxygen ring can be equivalent to a planar six-membered ring B₃O₆, and the vibrational bands of the crystal with this kind of ring can be attributed to the vibrational modes of the B₃O₆ ring and BO₄ tetrahedra. It is well known that 805 cm⁻¹ band, characteristic of vitreous B₂O₃, is assigned to the symmetric breathing vibration of the six-numbered ring^[18] which involves the motion of ring oxygen atoms only.^[19] Meanwhile the phenomenon of frequency shift toward low wavenumber with the increase of the number of BO₄ tetrahedron in the rings has also been observed recently in studies on boron-oxygen glasses.^[20] The structure of CsLiB₆O₁₀ (CLBO) crystal, reported by Wang,^[17] comprises the basic structure unit (B₃O₇) group which is a six-numbered ring in which two of the B atoms are three-fold coordinated and the third B atom is four-fold coordinated by O atoms. The Raman bands in the range of 782–785 cm⁻¹ observed in the spectra of CLBO crystal are assigned the ring-breathing vibrational mode of the six-numbered ring. The frequency of this mode shifts to 765 cm⁻¹ observed in the Raman spectrum of LiB₃O₅ (LBO) crystal^[21,22] consisting of boroxygen rings with one BO₄ tetrahedron. Therefore, the vibrational band at 746 cm⁻¹ in the Raman spectra of NVBO crystal may be related to the breathing vibration of the boroxygen ring which consists of two BO₄ tetrahedra. It is worth noting that its frequency of Raman vibration is lower than those of LBO and CLBO crystals with the same triborate group. On the other hand, the two BO₄ tetrahedra connect together with B–O–B bonds in the boroxygen ring. A tetrahedron molecule BO₄ with symmetry Td has four normal vibrational modes: v₁ (symmetric stretching mode), v₂ (bending mode), v₃ (asymmetric stretching mode), and v₄ (bending mode). The normal mode frequencies for a BO₄ tetrahedron may be approximated by Murray and Lockwood:^[23] v₁ ∼ 400 cm,⁻¹, v₂ ∼ 200 cm⁻¹, v₃ ∼ 1100 cm⁻¹, and v₄ ∼ 260 cm⁻¹. Here, the weak band located at 1119 cm⁻¹ (A₁ mode) is related to BO₄ asymmetric stretching mode vibration which is observed in the range of 1143–1166 cm⁻¹ in the spectra of LiNaB₄O₇ as reported by Maczka;^[24] the middle intense band at 465 cm⁻¹ is caused by the symmetric stretching mode vibration.

In the structure of the NVBO crystal, a three-dimensional framework is formed by VO₄ tetrahedra which, with V–O–B bonds, link sheets made up of polyborate [B₆O₁₃] groups. The VO₄ tetrahedra have four normal vibrational modes. Ross^[25] reported the infrared and Raman spectra of the free VO₄ ion. There are four vibrations for VO₄, namely, the v₁ (A₁) symmetric stretching mode located at around 874 cm⁻¹, the v₂ (E) bending mode in the region between 340 cm⁻¹ and 345 cm⁻¹, the v₃ (F₂) asymmetric stretching mode at 855 cm⁻¹ and the v₄ (F₂) bending mode at 345 cm⁻¹. Ross also reported the v₃ modes of vanadinites at 800 cm⁻¹ and 736 cm⁻¹ and the v₄ modes around 419 cm⁻¹, 380 cm⁻¹ and 322 cm⁻¹. Moreover, according to the analysis of the spectra of Pb5(VO4)Cl, Ray et al.^[26] reported that the Raman bands located at 879 cm⁻¹ and 827 cm⁻¹ are assigned to the ν₁ symmetric stretching vibration of the VO₄ ion and the Raman bands at 815 and 790 cm⁻¹ to the ν₃ mode. In this work we assigned the intense band 900 cm⁻¹ as relative to the v₁ symmetric stretching vibration. The band located at 817 cm⁻¹ is related to the ν₃ mode. In addition, the middle intense band located at 380 cm⁻¹ is due to O–V–O bending vibration mode. This assignment is in agreement with that proposed by Ray (v₄ in the range of 380–395 cm⁻¹).

3.3. High-temperature Raman spectra

The temperature-dependent Raman spectra of an NVBO crystal in the wavenumber range of 100–1600 cm⁻¹ were recorded with temperature increasing from room temperature to melting point, as shown in Fig. 3. Nearly all the vibrational modes exhibit a decrease in wavenumber. Figures 4 and 5 illustrate the wavenumber shifts of main Raman peaks. The Raman bands, such as 630 cm⁻¹, 744 cm⁻¹, 900 cm⁻¹, and 930 cm⁻¹, have wavenumber shifts more than 6 cm⁻¹. In particular, the Raman band located at 1309 cm⁻¹ has 22 cm⁻¹ wavenumber shifts. According to the report of Cerderira,^[27] the decrease in wavenumber with the increase of temperature is ascribed to the increase in the inter-atomic distance in the NVBO crystal when the crystal is heated. In addition, the Raman bands become wider during the heating process. The intense band at 900 cm⁻¹ becomes a shoulder at 930 cm⁻¹ after the temperature increases to 375 °C, as a consequence of larger distributions of the bonding angles and distances at higher temperature. These phenomena also appear in the high-temperature Raman spectra of Bi₁₂SiO₂₀, KTa1_1−xNb_xO₃, Ba₃(PO₄)₂, BiB₃O₆, and Bi₂ZnOB₂O₆ crystals.^[28–32] The weak band at 950 cm⁻¹ becomes overlapped and merges together with the band at 930 cm⁻¹ after the temperature increases to 150 °C. However, the spectra of the NVBO crystal do not show any splitting or new bands, which indicates that no phase transition occurs under 525 °C in the present study. However, the Raman spectrum of NVBO crystal becomes dramatic when the temperature increases to the melting point (about 610 °C). Some Raman bands, such as 176, 278, 465 and 630 cm⁻¹, disappeared in the spectrum of the melt due to the transformation of the crystal structure during melting. It should be noted that vanishing of the band at 465 cm⁻¹ related to the BO₄ vibration implies the break of B–Ø bonds in BO₄ tetrahedron and change from the 4- to 3-coordinated boron during melting.

	Figure Option View Download New Window
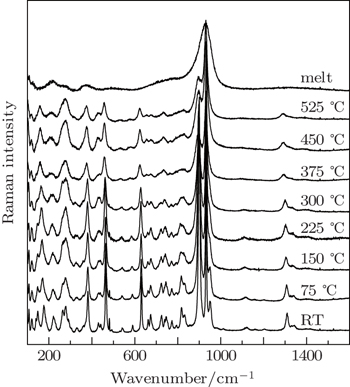	Fig. 3. High-temperature Raman spectra of Na₃VO₂B₆O₁₁ crystal from room temperature to melting point.

	Figure Option View Download New Window
	Fig. 4. The wavenumber shifts of Raman peaks with temperature increasing at different frequencies. The lines from top to bottom mean 380 cm⁻¹, 276 cm⁻¹, 220 cm⁻¹, and 178 cm⁻¹, respectively.

	Figure Option View Download New Window
	Fig. 5. The wavenumber shifts of Raman peaks with temperature increasing at different frequencies. The lines from top to bottom mean 1304 cm⁻¹, 932 cm⁻¹, 900 cm⁻¹, 746 cm⁻¹ and 630 cm⁻¹, respectively.

3.4. Raman spectra of the melt

The fitting results in the range of 600–1100 cm⁻¹ are shown in Fig. 6 to explain the micro-structure of the melt. It is reported by some authors that atom clusters exist in the melt. In order to investigate the atom clusters in the melt, the ab initio calculation was performed with Gaussian98W program.^[33] The Raman spectra of two model clusters, VO₄ tetrahedron and VBO₆ cluster made up of VO₄ tetrahedron and BO₃ triangle connected by one bridge oxygen, are calculated by a restricted Hatree–Fock method of the quantum chemistry ab initio calculation^[34] with the 6–31G(d) basis set. Experimental spectra have also been presented to make a comparison with the calculated results. The main vibrational bands between the curve calculated and fitting results agree approximately well with each other as a whole. The Raman bands can be recognized with the aid of the GaussView software. The vibration bands at 928 cm⁻¹ (934 cm⁻¹ in calculation) and 1300 cm⁻¹ (1294 cm⁻¹ in calculation) are related to the B–O stretching vibrations in VBO₆ clusters. The band located at 797 cm⁻¹ (786 cm⁻¹ in calculation) can be assigned as the bending vibration of B–Ø–V bridge oxygen. It also demonstrated that the bands at 884 cm⁻¹ (893 cm⁻¹ in calculation) and 946 cm⁻¹ (944 cm⁻¹ in calculation) represent the V–O vibration of free VO₄ tetrahedron. These arguments make the following conclusion that the crystal framework collapses with the break of B–Ø bonds in BO₄ tetrahetra to form VO₄ and VBO₆ clusters existing in the melt.

	Figure Option View Download New Window
	Fig. 6. Raman spectra of melt of Na₃VO₂B₆O₁₁ crystal and calculation of VO₄ and VBO₆ groups; the fitting result in the shoulder picture.

4. Conclusion

High-temperature Raman spectroscopy has been used to investigate the micro-structure of NVBO crystals and its melt. The obtained results coincided well with experimental results. Raman spectra of single crystal NVBO were recorded in the spectral range of 10–1600 cm⁻¹ at room temperature first. Then the changes of the Raman peaks and the crystal structure were investigated at high temperature. It was found that all the Raman peaks exhibit decreases in frequency and the widths of the Raman peaks increase with temperature increasing. No phase transition was observed under 525 °C. Lastly, the micro-structure of its melt was studied by quantum chemistry ab initio method. The VO₄ and VBO₆ clusters exist in the melt.

Reference

1	Nador B 1964 Nature 201 921
2	Buludov N TMamedaliev F DKaraev Z SAbdullaev G K1985Russ. J. Inorg. Chem.301032
3	Ditrich V INakhodnova A P1992Russ. J. Inorg. Chem.371097
4	Touboul MPenin NNowogrocki G 2000 J. Solid State Chem. 150 342
5	Fan X YPan S LHou X LTian X L 2010 Cryst. Growth Des. 10 252
6	Krogh-Moe J 1962 Acra Crystallogr. 15 190
7	Mori YKuroda INakajima S 1995 J. Cryst. Growth 156 307
8	Chen C TWu YJiang A 1989 J. Opt. Soc. Am. B 6 616
9	Pereira KSilva DSantos JMaczka MParaguassu WFreire P TMendes F JHanuza J 2013 J. Solid State Chem. 199 7
10	Calizo IBalandin A ABao WMiao FLau C N 2007 Nano Lett. 7 2645
11	Hou MYou J LSimon PZhang G CWan S MWang Y YJi Z FWang L HFu P ZWu Y CYin S T 2011 Cryst. Eng. Commun. 13 3030
12	Zhang JWang DZhang D MZhang Q LWan S MSun D LYin S T 2013 Acta Phys. Sin. 62 037802 (in Chinese)
13	Zhang J MRuf TCardona MAmbacher OStutzmann MWagner J MBechstedt F 1997 Phys. Rev. B 56 14399
14	Rafailov P MEgorysheva A VMilenov T IVolodin V DAvdeev G VTitorenkova RSkorikov V MPetrova RGospodinov M M 2010 Appl. Phys. B 101 185
15	Elalaoui E AMaillard AFontana M D 2005 J. Phys.: Condens. Matter 17 7441
16	Xiong GLan GWan H 1993 J. Raman Spectrosc. 24 785
17	Wang Y FLiu J JHu S FLan G X 1999 Spectrochimica Acta Part A 55 2565
18	BrillPhilips T W1976Res. Rep. Suppl.No. 2
19	Windisch C FRisen W M 1982 J. Non-Cryst. Solids 48 307
20	Farmer V C1974Mineralogical: The Infrared Spectra of Minerals
21	Wang DWan S MYin S TZhang Q LYou J LZhang G CFu P Z 2011 Cryst. Eng. Commun. 13 5239
22	Maslyuk V VBredow TPfnur H 2004 Eur. Phys. J. B 42 461
23	Murray A FLockwood D J 1976 J. Phys. C: Solid State Phys. 9 3691
24	Maczkaa MWaskowskaa AMajchrowskib AZmijab JHanuzaa JPetersond G AKeszler D A 2007 J. Solid State Chem. 180 410
25	Ross S D1972Inorganic Infrared and Raman SpectraMcGraw-HillNew York
26	Ray LFrostMartin CPeter AWilliamsKloprogge J T 2003 J. Raman Spectrosc. 34 214
27	Cerderira FMelo F E ALemos V 1983 Phys. Rev. B 27 7716
28	Qiu H LWang A HYou J LLiu X JChen HYin S T2005Spectroscopy and Spectral Analysis25222
29	Zhou W PWan S MYin S TZhang Q LYou J LWang Y Y2009Acta Phys. Sin.580570(in Chinese)
30	Zhang JWang DZhang D MZhang Q LWan S MSun D LYin S T 2013 Acta Phys. Sin. 62 097802 (in Chinese)
31	Wan S MTeng BZhang XYou J LZhou W PZhang Q LYin S T 2010 Cryst. Eng. Commun. 12 211
32	Zhang JZhang D MZhang Q LYin S T 2015 Chin. Phys. B 24 017801
33	Gaussian WFrisch M JTrucks G WSchlegel H Bet al.1998Gaussian Inc.(Pittsburgh, PA)
34	Takenobu SMasahiro HHideo H 2002 J. Appl. Phys. 91 4149