In the last few decades, a large amount of work has been devoted to the research on the physics character of exciton, polaron, and impurity properties of semiconductor heterostructures, such as quantum wells, quantum wires, quantum dots, superlattices, films on substrates, etc. Such interest has arisen due to the physics nature underlying various properties of these systems and the potential applications in a wide range of electronic and optoelectronic devices. In fact, excitons have great effects on a variety of physical phenomena observed in these structures. Therefore understanding these properties such as the increase in the exciton binding energy due to the confinement of the carriers has become an important topic in the study of low-dimensional structures in the last few decades.

Since the pioneering work on exciton in a polar crystal by Haken,^[1] a great deal of work has been devoted to study the excitonic properties in films theoretically and experimentally. Several authors calculated the binding energies of excitons in free-standing GaAs films by using variational schemes.^[2] The optical spectroscopy of large-momentum excitons in GaAs films was experimentally and theoretically investigated by some researchers.^[3,4] Photoluminescence (PL) spectrum measurements were used to study exciton^[5,6] and exciton–polariton^[7] problems and to determine the exciton binding energies^[8,9] in various semiconductor films, such as CdS, ZnSe, GaN, and CsSnI₃ films. In particular, the GaAs film on Al_xGa_1−xAs substrate is an important semiconductor low-dimensional structure. As far as we know, there is not much work on the exciton properties in a GaAs film on an Al_xGa_1−xAs substrate.

Of particular interest to the present work is the fractional-dimensional approach (FDA) first proposed by He^[10–13] to study excitons and optical properties of anisotropic solids. In this approach, the Schrödinger equation for a real anisotropic system is solved in a noninteger-dimensional space where the interactions are assumed to occur in an isotropic effective environment, and the essential quantity is the fractional dimension D associated with the effective medium and the degree of anisotropy of the actual system. In the last few years, the FDA has been successfully used in the study of the excitons,^[14–18] biexcitons,^[19–21] magnetoexciton,^[22–24] excitonic and impurity states,^[23,25–30] polarons,^[31–34] and exciton–phonon interaction^[35–38] in anisotropic semiconductor heterostructures. However, to the best of our knowledge, the FDA has not been extended to investigate excitons in a GaAs film on an Al_xGa_1−xAs substrate.

In our preview work, we used the FDA to study the polaron effect in a GaAs film deposited on Al_xGa_1−xAs substrate.^[39–41] In this paper, we extend the FDA to the case of an exciton confined to a GaAs film on Al_xGa_1−xAs substrate. Within the FDA, the exciton + GaAs film system is realistically described by an equivalent isotropic hydrogenic system in a fractional D-dimensional space, a problem which can be solved analytically. As functions of the film thickness, the exciton binding energies are calculated. This paper is organized as follows. In Section 2, the theoretical framework of the FDA is extended to the case of excitons confined in GaAs films on Al_xGa_1−xAs substrates. Numerical results and discussion are given in Section 3, and conclusions are given in Section 4.

Let us consider the problem of an exciton confined in a semiconductor GaAs film on Al_xGa_1−xAs substrate (growth axis along the z direction). Within the effective mass and the parabolic band approximations, the Hamiltonian for the exciton can be given by

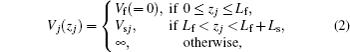
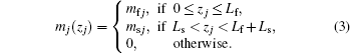
Using the FDA proposed by He,^[10–13] the exciton problem in an anisotropic solid can be treated as one in an isotropic fractional-dimensional space whose dimension D depends on the degree of anisotropy of the real system. By utilizing the Laplacian operator proposed by Stillinger,^[42] who proposed axioms and operators for a noninteger-dimensional space, the discrete bound-state energies and orbital radii are given by

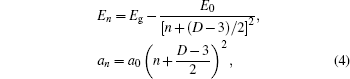
According to Eq. (4) and in the case of our GaAs film–Al_xGa_1−xAs substrate system, the binding energy of the 1s exciton can be written as

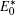
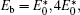
In our GaAs film–Al_xGa_1−xAs substrate system, within the effective mass and the parabolic band approximations, the Hamiltonian for the single electron (j = e) or hole (j = h) can be given by

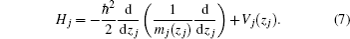
The dimensional parameter D that guarantees the mapping of the real system into the fractional-dimensional space can be calculated through the relation^[31]

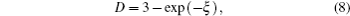
In the case of an exciton confined in a GaAs film on Al_xGa_1−xAs substrate, the exciton is no longer restricted to the region inside the film only. Therefore, the spreading of the exciton wave function into the substrate has to be considered in defining the corresponding length of confinement. Taking into account the spatial extension of the exciton motion in the substrate region, the length of confinement is characterized by an effective film thickness which may be written as

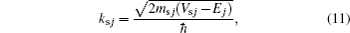
On the other hand, the effective length that characterizes the electron–hole interaction is the mean value of the effective Bohr diameter of the 3D exciton

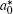
Therefore, the dimensional parameter D can be calculated through the relation

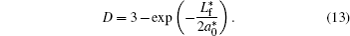
In the GaAs film–Al_xGa_1−xAs substrate system, the material parameters which characterize the exciton properties differ when passing from the film to the substrate region. In other words, the effective-mass mismatch between the film and the substrate materials should be considered. In order to take this fact into account, we may assign the effective fractional-dimensional space an average of the material parameters over the exciton positions. The mean values of the material parameters can be calculated in the same manner as in Ref. [43]. In this way, they enter in the Hamiltonian of the system and weight the spatial integration with the square module of the electron (j = e) and hole (j = h) wave functions Ψ_j(z_j) determined by H_j (Eq. (7)). Our effective fractional-dimensional exciton is then characterized by the following set of mean material parameters:

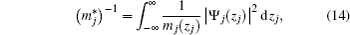
Finally, the binding energy of an exciton confined in a GaAs film on Al_xGa_1−xAs substrate can be obtained in an analytical way from Eqs. (5), (6), and (13) with the mean values of the material parameters defined in Eqs. (14) and (15). We use the same set of material parameters as discussed by Smondyrev et al.^[43] in our calculations. The numerical results are discussed in Section 3.

The binding energy of the heavy-hole exciton in the GaAs film on Al_xGa_1−xAs substrate as a function of the film thickness is displayed in Fig. 1, for different Al concentrations at the substrate thickness L_s = 20 Å. As can be seen, the exciton binding energy first increases as the film thickness decreases for different Al concentrations, as long as the exciton wave function remains confined in the film region. For thin films, the wave function starts to penetrate into the substrate and the exciton binding energy actually begins to decrease as the film thickness is reduced. Therefore, the exciton binding energies exhibit maxima at the film thicknesses L_f ≈ 58 Å for x = 0.2, L_f ≈ 44 Å for x = 0.3, and L_f ≈ 35 Å for x = 0.4. Notice that this behavior was also obtained in the case of excitons in GaAs–Al_xGa_1−xAs quantum wells by using the FDA.^[14,18] It is also worthwhile noting that different Al concentrations have a significant influence on the exciton binding energy in thin and medium films, but have no significant influence in thick films. This behavior was also obtained in the case of excitons in GaAs–Al_xGa_1−xAs quantum wells by using the FDA.^[14,18]

Fig. 1.

	Figure Option ViewDownloadNew Window
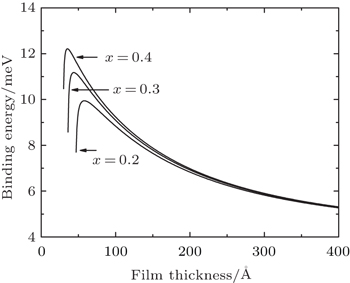	Fig. 1. The heavy-hole exciton binding energy in the GaAs film on AlxGa1−xAs substrate as a function of the film thickness for different Al concentrations at the substrate thickness Ls = 20 Å.

The fractional dimension D corresponding to the fractional-dimensional result in Fig. 1 is shown in Fig. 2 as a function of the film thickness. With an extremely thick film, the system behaves as a GaAs bulk and consequently the fractional dimension approaches to the limit value D = 3. When the film thickness decreases, the system becomes more and more confined, the exciton becomes more compressed, and the effective dimension decreases, reaching minima at the film thicknesses L_f ≈ 60 Å for x = 0.2, L_f ≈ 47 Å for x = 0.3, and L_f ≈ 39 Å for x = 0.4. Notice that this behavior was also predicted in the case of excitons in GaAs-Al_xGa_1−xAs quantum wells within the FDA.^[14,18] As the film thickness continues to decrease and is less than the exciton size, the exciton wave function starts to leak into the substrate so that the fractional dimension begins to increase. It is also worth remarking that different Al concentrations have a significant influence on the fractional dimension for thin and medium films, but have no significant influence for thick films. This behavior was also predicted in the case of excitons in GaAs-Al_xGa_1−xAs quantum wells within the FDA.^[14,18]

Fig. 2.

	Figure Option ViewDownloadNew Window
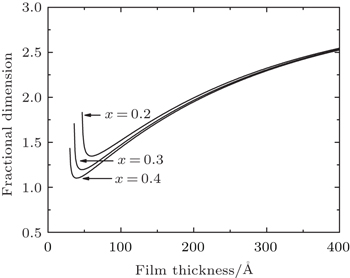	Fig. 2. The corresponding fractional dimension D as a function of the film thickness for different Al concentrations at the substrate thickness Ls = 20 Å.

The binding energy of the heavy-hole exciton in the GaAs film on Al_0.3Ga_0.7As substrate as a function of the film thickness is displayed in Fig. 3, for different substrate thicknesses L_s = 20 Å, 50 Å, 100 Å. It can be seen that for different substrate thicknesses, the exciton binding energy has a maximum as the film thickness increases. The maxima appear at the film thicknesses L_f ≈ 44 Å, 35 Å, 31 Å, respectively. We note that the exciton binding energy increases with increasing substrate thickness. This is due to the ratio of the GaAs film–Al_xGa_1−xAs substrate material parameters. It is also worth noting that different substrate thicknesses have a significant influence on the exciton binding energy for thin films but have no significant influence for thick films.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The heavy-hole exciton binding energy in the GaAs film on Al0.3Ga0.7As substrate as a function of the film thickness at different substrate thicknesses Ls = 20 Å, 50 Å, 100 Å.

The fractional dimension D corresponding to the fractional-dimensional result in Fig. 3 is shown in Fig. 4 as a function of the film thickness. For different substrate thicknesses, a structure with a minimum is obtained in the behavior of the fractional dimension. The minima appear at the film thicknesses L_f ≈ 47 Å, 46 Å, 46 Å, respectively. It is also observed that, different substrate thicknesses significantly influence the fractional dimension for thin films but have no significant influence for thick films.

Fig. 4.

	Figure Option ViewDownloadNew Window
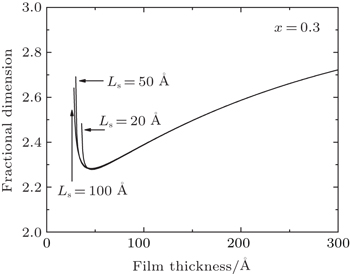	Fig. 4. The corresponding fractional dimension D as a function of the film thickness at different substrate thicknesses Ls = 20 Å, 50 Å, 100 Å.

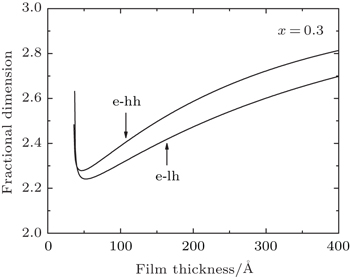
The binding energies for the heavy-hole and light-hole excitons in the GaAs film on Al_0.3Ga_0.7As substrate as a function of the film thickness are displayed in Fig. 5, with the substrate thickness L_s = 20 Å. It is seen that the binding energies for the heavy-hole and light-hole excitons both exhibit their maxima with increasing film thickness. The maxima appear at the film thicknesses L_f ≈ 44 Å for the heavy-hole exciton and L_f ≈ 50 Å for the light-hole exciton. It is easily understood that the binding energies for the heavy-hole and light-hole excitons first increase as the film thickness decreases for the thicker film case, since the exciton wave function remains mainly confined in the film region. Once the film thickness is reduced and less than the exciton size, the exciton wave function will penetrate into the substrate region so that the binding energies decrease suddenly. We note that the heavy-hole exciton binding energy begins to decrease later than the light-hole one as the film thickness decreases. This is due to the z-direction effective masses. This behavior was also obtained by using the FDA in the case of excitons in GaAs-Al_xGa_1−xAs quantum wells.^[14] It can also be seen that at a certain film thickness, the heavy-hole exciton binding energy is larger than the light-hole one because of the ratio of the in-plane effective masses. It is noteworthy that this result is quite different from the case of excitons in GaAs–Al_xGa_1−xAs quantum wells.^[14] This should be due to the different definition of effective masses for the heavy-hole and light-hole excitons in Ref. [14]. In this paper, we use a consistent set of material parameters as discussed in Ref. [43].

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The binding energy for the heavy-hole and light-hole excitons in the GaAs film on Al0.3Ga0.7As substrate as a function of the film thickness at the substrate thickness Ls = 20 Å.

The fractional dimension D corresponding to the fractional-dimensional result in Fig. 5 is shown in Fig. 6 as a function of the film thickness. For both heavy-hole and light-hole excitons, a structure with a minimum is predicted in the behavior of the fractional dimension. The minima appear at the film thicknesses L_f ≈ 47 Å for the heavy-hole exciton and L_f ≈ 53 Å for the light-hole exciton. On account of the z-direction effective masses, the heavy-hole exciton fractional dimension begins to increase later than the light-hole one as the film thickness decreases. We note that, for relatively thick films, the light-hole exciton fractional dimension is smaller than the heavy-hole one at a certain film thickness because of the ratio of the in-plane effective masses. The result for relatively thick films is due to the fact that the light-hole exciton is more compressed by the system.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The corresponding fractional dimension D for the heavy-hole and light-hole excitons as a function of the film thickness at the substrate thickness Ls = 20 Å.

We have used the FDA, in which the real anisotropic semiconductor system is mapped into an effective isotropic space with a fractional dimension, to study the exciton binding energies in GaAs films on Al_xGa_1−xAs substrates. For different aluminum concentrations and substrate thicknesses, the exciton binding energies are obtained as a function of the film thickness. The numerical results show that, for different aluminum concentrations and substrate thicknesses, the exciton binding energies in GaAs films on Al_xGa_1−xAs substrates all exhibit their maxima with increasing film thickness. It is also shown that the binding energies of heavy-hole and light-hole excitons both have their maxima with increasing film thickness. Moreover, the heavy-hole exciton binding energy is larger than the light-hole one at a certain film thickness, which is quite different from the case of excitons in GaAs-Al_xGa_1−xAs quantum wells.