Cite this Article
Lan Hui, Wang Xin-Bing, Zuo Du-Luo. Spectral and ion emission features of laser-produced Sn and SnO2 plasmas. Chinese Physics B, 2016, 25(3): 035202  
Permissions
Spectral and ion emission features of laser-produced Sn and SnO2 plasmas
Lan Hui1, 2, Wang Xin-Bing3, †, , Zuo Du-Luo3
School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China
School of Physics and Information Engineering, Jianghan University, Wuhan 430056, China
Wuhan National Laboratory for Optoelectronics (WNLO), Wuhan 430074, China

 

† Corresponding author. E-mail: xbwang@hust.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 11304235) and the Director Fund of WNLO, China.

Abstract
Abstract

We have made a detailed comparison of the atomic and ionic debris, as well as the emission features of Sn and SnO2 plasmas under identical experimental conditions. Planar slabs of pure metal Sn and ceramic SnO2 are irradiated with 1.06 μm, 8 ns Nd:YAG laser pulses. Fast photography employing an intensified charge coupled device (ICCD), optical emission spectroscopy (OES), and optical time of flight emission spectroscopy are used as diagnostic tools. Our results show that the Sn plasma provides a higher extreme ultraviolet (EUV) conversion efficiency (CE) than the SnO2 plasma. However, the kinetic energies of Sn ions are relatively low compared with those of SnO2. OES studies show that the Sn plasma parameters (electron temperature and density) are lower compared to those of the SnO2 plasma. Furthermore, we also give the effects of the vacuum degree and the laser pulse energy on the plasma parameters.

PACS: 52.38.–r;52.38.Mf;52.70.–m;52.70.La;
Keyword:laser-produced plasma;Nd:YAG laser;ion emission;extreme ultraviolet emission;
1. Introduction

Extreme ultraviolet (EUV) sources based on laser-produced plasma (LPP) are believed to be capable of meeting basic EUV lithography (EUVL) requirements, which are high EUV conversion efficiency (CE) and cleanliness of the source.[1–4] It is well known that the laser properties, the target material, as well as the buffer gas affect the LPP EUV radiation. The main mechanism of the absorption in laser–target interaction is the inverse bremsstrahlung (IB) absorption, which is inversely proportional to the laser wavelength. Due to the shorter wavelength of the Nd:YAG laser, more laser energy is absorbed by the plasma, and the critical density of the plasma is larger compared with that of the CO2 laser (∼1021 cm−3 for 1.06 μm and ∼1019 cm−3 for 10.6 μm). Nd:YAG laser produced plasma EUV sources can be used as metrology light sources,[5] while CO2 laser produced plasma EUV sources are used as high volume manufacturing (HVM) sources.[6] Moreover, the Nd:YAG laser has a better optical beam quality, which results in a higher power density than that of the CO2 laser and creates highly-ionized species. A number of different target materials are considered for EUV sources, including Li, F, Sn, and Xe.[7–11] Among these analyzed targets, Sn has been found to be the most promising target material for 13.5 nm wavelength with a high CE of > 2%.[12,13] To obtain a higher CE, researchers have come up with new ideas for the Sn target. Hayden et al.[14] used ceramic slab targets doped with 5% and 6% Sn and an Nd:YAG laser for the EUV source. The results showed that the 5% (i.e., low density) Sn doped ceramic target had a maximum EUV CE of over 2.5% at the laser pulse intensity of 1.91 × 1011 W·cm−2, but the EUV CE of the Sn doped target was not always higher than that of pure Sn, because the EUV CE also varied with the laser power density. Xin et al.[15] compared the EUV radiation signals from Nd:YAG laser produced plasmas in Sn and low density SnO2/CNTs nano-composites using an AXUV-100 silicon photodiode. They found that the EUV radiation signal of the pure Sn target was quite strong at high laser pulse energy compared to that of the low density SnO2/CNTs nano-composites target, while the emitted EUV signals were approximately the same at low laser pulse energy. Tao et al.[16] also investigated the properties of EUV emission from pure Sn, 59% SnO2, and 23% SnO2 targets using an Nd:YAG laser. Their results showed that the EUV emission was increased with an increase in the fraction of Sn at a fixed laser intensity. Apart from high EUV CE, the ion and atom debris also affect the generated plasma emission. However, the plasma plume expansion and ion debris were not studied in detail.

To further study the Sn-based EUV source in this paper, we present a complete analysis of the parameters of the plasma generated from two planar slab LPP targets (metal Sn and ceramic SnO2) under identical experimental conditions. The Sn and SnO2 plasmas are generated by an Nd:YAG laser with a pulse width of 8 ns (FWHM) at the wavelength of 1.06 μm producing a maximum energy of 216 mJ in vacuum conditions. Time-integrated EUV image spectra are obtained and analyzed using a grazing incidence flat-field spectrograph coupled with an x-ray CCD camera. The EUV CE is deduced under different vacuum degrees. The plasma plume emission and expansion dynamics are estimated by means of fast gated photography using a fast gated intensified charge coupled device (ICCD) imaging system. Moreover, the Faraday cup (FC) measurements permit us to obtain the time of flight (TOF) signals. Optical emission spectroscopy (OES) measurements are performed in the visible range and reveal detailed information about the dynamics of spectral emission. Temporal evolution of the plasma parameters (electron temperature and density) has been determined by the Boltzmann plot method and Stark line broadening. In addition, the effects of the different vacuum degrees on the plasma parameters are studied.

2. Experiment setup

The experimental apparatus is shown schematically in Fig. 1. The chamber and the EUV detection system were evacuated to a pressure of 10−3 Pa with a turbo-molecular pump. An Nd:YAG laser (Innolas, SpitLight Compact 200) operated at 1 Hz, 1.064 μm was focused onto the target at the center of the chamber using a plano-convex lens (f = 100 mm) with an angle of 45° to the target surface normal. The estimated spot size at the target surface was 100 μm and the maximum power density at the target surface was 3×1011 W·cm−2. The 5 mm thick and 100 mm diameter planar slabs of metal Sn and ceramic SnO2 were used as the targets. The purity of materials was higher than 99.5%. The target was mounted on a mechanically rotated XY translational stage, which provided fresh surface exposure for each measurement.

Fig. 1. Schematic of the experimental setup (L1, L2: lens; SM: spherical mirror; FM: flat mirror).

A grazing incidence flat-field spectrograph with a periodically ruled concave gold coated flat-field grating of radius 5649 mm (fabricated by Hitachi, Ltd.) was built to detect the EUV emission from LPP. The detector was a 1340×400 pixel array back-illumination-type x-ray CCD (Princeton Instruments), which recorded the EUV emission normal to the target surface. Zr film filters with a thickness of 500 nm were used to block visible light and pass EUV radiation for the spectrograph. The transmittance of the Zr filters at 13.5 nm was about 20%.

For fast-gated imaging, the integrated visible emission from the expanding plasma was collected through a quartz window normal to the direction of expansion using an ICCD (Princeton Instruments) camera. A Nikon lens (f = 105 mm, F/2.8 D) was used to image the plume region onto the camera to form a two-dimensional image of the plume intensity. The gate width was set at 7 ns. The temporal evolution of plasma could be tracked by the delay of the ICCD’s gate.

Ions from LPP were monitored by an FC placed at a distance of 160 mm from the target at an angle of 30° with respect to the normal. The FC consisted of two electrically isolated copper concentric cylinders and the aperture of the FC was 6 mm. To minimize the impact of the secondary electron current, the inner cylinder was negatively biased at −20 V with respect to the grounded outer cylinder. The IC output signal was acquired across a 50 Ω load resistor using a 350 MHz storage oscilloscope (Agilent, DSO-X 3034A).

The emission from the plasma was collected by an optical fiber normal to the direction of the plasma expansion. The optical fiber was connected to the entrance slit of a Princeton SP2750i spectrograph with a focal length of 750 mm equipped with a 300 grooves/mm grating. The spectrograph used in the experiment was an Acton SP2750i with a focus length of 750 mm. The optimum resolution was obtained at the slit width of 20 μm. The spectrograph and ICCD combination provided a maximum resolution of 0.012 nm. An ICCD (PI-MAX-1300) camera was installed at the exit of the spectrograph.

3. Results and discussion
3.1. EUV emission features

Laser pulses of 216 mJ and a fixed spot size of 100 μm are used to obtain the EUV emission from Sn and SnO2 plasmas. Figures 2(a) and 2(b) show the measured EUV emission spectra from both targets with the increase of the gas pressure. The EUV spectra of Sn and SnO2 plasmas exhibit similar line structures and the peaks in the spectra are around 13.5 nm, because the principal quantum number of the transitions (the 4d to 4f transitions between Sn8+ and Sn13+ ions) does not change. The difference in the spectra lies in that the EUV emission from the ceramic SnO2 target has a narrower bandwidth than that from the Sn metal target. Similar spectral narrowing was observed in Sn compound targets.[17] It is concluded that less dense Sn ions in an Sn-based target result in lower EUV generation. Moreover, the intensity of the EUV spectrum decreases with increasing background gas pressure and most of the EUV radiation photons are absorbed when the pressure is higher than 10 Pa.

Fig. 2. EUV emission spectra from (a) metal Sn and (b) ceramic SnO2 targets measured by a flat-field grating spectrograph.

The dependence of the in-band EUV CE on the vacuum degree is evaluated for both plasmas, as shown in Fig. 3. Generally, the EUV CE is estimated by the following equation:[18]

where N is the total photon counting; h is the Planck constant; v is the laser frequency corresponding to the wavelength of 13.5 nm; η1 is the transmission efficiency of extreme ultraviolet; η2 is the grating diffraction efficiency; η3 is the light acceptable percentage of the spherical mirror; η4 is the conversion efficiency of CCD; and E is the incident laser pulse energy.

Fig. 3. EUV CE at 13.5 nm of plasmas formed from pure Sn target and ceramic SnO2 target varies with the vacuum degree. The smooth curves represent best fits obtained with exponentially saturating curve fitting.

As can be seen from Fig. 3, the Sn plasma provides a higher CE, reaching a peak level of 1.03%, as opposed to a peak of 0.69% for the SnO2 LPP plasma at the ambient pressure of 10−3 Pa. The EUV CE of both plasmas is decreased with an increase in the gas pressure, because the radiation is absorbed by the gas in the chamber.

3.2. Plasma plume expansion

In addition to radiating the 13.5 nm in-band light, numerous neutral particles are produced by the plasma expansion. We use fast gated imaging employing ICCD for capturing hydrodynamic expansion features of Sn and SnO2 plasma plumes at various vacuum degrees. Typical intensity normalized images obtained after the laser irradiation are shown in Fig. 4. The radiation from the plasma is recorded integrally in a wavelength range from 300 nm to 900 nm. The colors in the ICCD camera images indicate different radiation intensities. The white color region in the center of the plume may correspond to the areas of highest temperature and particle density in the plasma plume. The observed forward movement of both Sn and SnO2 plasma edges increases as the pressure decreases at the same delay. This is because the collisions between the plasma ions and the gas particles in the vacuum chamber result in the reduction of the velocity and the kinetic energy of the plasma ions. From these images, it is obvious that both plasma plumes show a spherical geometry. While the SnO2 LPP plumes are found to expand with a stronger forward bias in directions normal to the target surface. The light mass of O ions may cause the higher expansion speed of the SnO2 plasma. With the same laser pulse energy, the mass ablation in the case of the SnO2 target is greater than that of the Sn target, thus the diameter of the plasma emission from the SnO2 plasma is larger than that from the Sn plasma.

Fig. 4. Raw ICCD images of Sn and SnO2 plasma plumes with different vacuum degrees ((a) 1 Pa, (b) 10−1 Pa, (c) 10−3 Pa) and laser pulse energy of 216 mJ. Timing starts when the laser reaches the targets. A gate width of 7 ns is used for obtaining these ICCD images.
Fig. 5. Raw ICCD images of SnO2 plasma plumes with different vacuum degrees ((a) 1 Pa, (b) 10−1 Pa, (c) 10−3 Pa) and laser pulse energy of 216 mJ. Timing starts when the laser reaches the targets. A gate width of 7 ns is used for obtaining these ICCD images.

Figure 6 shows the maximum kinetic energy (KE) under different vacuum degrees recorded at a delay of 52 ns after the onset of plasma formation. The KE is computed by multiplying the half atomic mass with the square of the ion speed obtained from the front position change within the time delay. The mass is that of atomic Sn. It is apparent that, with the increase of the pressure, the ion kinetic energy gradually decreases due to the collision with the air molecules. With the increase of the delay time or the pressure, the kinetic energy would decrease non-linearly.

Fig. 6. KEs of Sn and SnO2 plasmas as a function of the vacuum degree.
3.3. Ion analysis

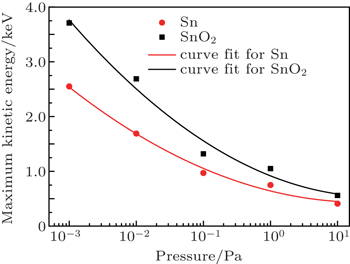
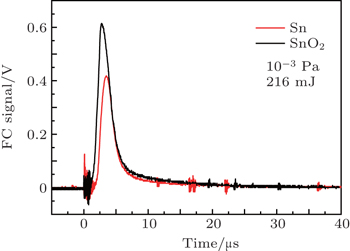
Similar results are observed in the ion debris analysis. We compare the ion emissions from Sn and SnO2 plasmas using an FC. TOF ion profiles obtained are shown in Fig. 7. In these measurements, the laser is maintained at an intensity of 3×1011 W/cm2, the spot size is 100 μm, and the pressure is 103 Pa. The ion TOF profile is characterized by a fast peak at the time close to zero, followed by a broad and higher peak. The fast and lower peak in the ion signal is caused by the photoelectric effect, and can be used as a zero-time marker. The broad and higher peak is resulted from the Sn ions of the plasma and a kinetic energy distribution of the Sn ions causes the broad peak and its long tail. It can be seen that the Sn ions possess a narrower kinetic profile compared to the SnO2 ions. The total number of ions emitted from the SnO2 plasma is larger than that from the Sn plasma. For the Sn plasma, the peak of the broad ion collection signal corresponds to those ions with an intensity of 0.4 V, compared with a peak ion collection signal of 0.63 V for the SnO2 plasma.

Fig. 7. Typical ion TOF signals obtained from FC for various target materials (Sn and SnO2).

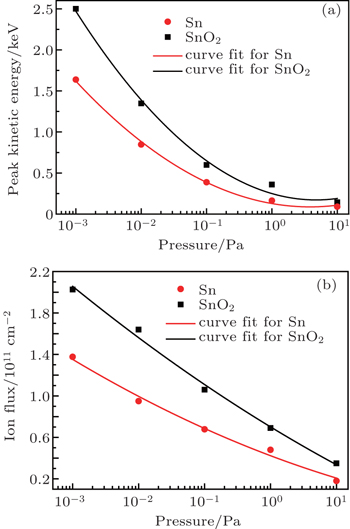
The maximum probable KEs as well as the ion fluxes of Sn and SnO2 plasmas at different vacuum degrees are shown in Fig. 8. For both Sn and SnO2 plasmas, the peak KEs and the ion fluxes show an exponential decay trend due to plasma shielding and absorption. Comparing the ion peak kinetic energies of Sn and SnO2 plasmas, one can notice that the peak kinetic energies are always higher in the SnO2 plasma, e.g., the ion peak KE of the Sn plasma is 1.63 keV and that of the SnO2 plasma is 2.5 keV at the pressure of 10−3 Pa. These results can be attributed to the amount of mass removed from the sample and the optical parameters of the plasma. As the concentration of O ions in the plasma increases from pure Sn metal to pure SnO2 ceramic, the number of ion debris increases and the ion kinetic energy of the SnO2 plasma becomes higher. These results are in agreement with the experiment results of the plasma plume in the previous section. The ion flux can be written as[19]

where jp (A/cm2) is the peak ion current density, τ (s) is the FWHM of the ion signal, and e is the electron charge (1.6 × 10−19 C). For Sn ions, jp is 1.12 × 10−2 A/cm2, τ is 2 × 10−6 s, so the ion flux is calculated to be 1.4 × 1011 ions/cm2. Amano et al.[20] studied the ion flux of Xe assuming a charge state of +2. Verbraak et al.[21] studied the energy distributions of Sn ions with the assumption of a constant ionization level. So in our experiment, we assume that the Sn ions are in the same charge state.

Fig. 8. (a) The maximum probable KEs and (b) the ion fluxes of Sn and SnO2 plasmas as a function of the vacuum degree. The smooth curves represent best fits obtained with an exponentially saturating curve fitting. The ion flux is calculated assuming the same charge state for all ions.
3.4. Emission spectrum

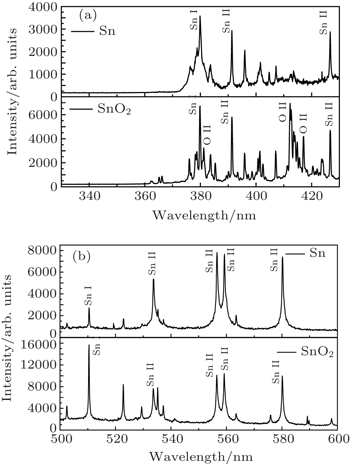All the spectra in the wavelength region of 200–700‘nm are collected and the time evolution spectra from laser-produced Sn and SnO2 plasmas are observed in two spectral regions (330–430 nm and 500–600 nm), monitored at 100 ns delay with a fixed gate width time of 7 ns, as shown in Figs. 9(a) and 9(b). The targets and experiment conditions in the emission measurement are practically identical to those described above. It shows that the emission spectrum of the SnO2 plasma mainly consists of transition lines of O I and O II, covering the range of 330–430 nm, and the central wavelength is set to 380 nm. Both emission spectra reveal that Sn I and Sn II lines are mainly observed between 500 nm and 600 nm and the central wavelength is set to 550 nm. In these figures, the atomic/ionic line positions and relative intensities of O I, O II, Sn I, and Sn II are listed according to the NIST atomic spectral database.[22]

Fig. 9. Emission spectra of Sn and SnO2 plasmas generated by Nd:YAG laser at a delay time of 100 ns: (a) 330–430 nm spectral region, (b) 500–600 nm spectral region.

Using OES, we estimate the electron temperature and density of laser ablation plumes. At early time, most of the emission is the continuous spectrum from plasma. As time evolves, the line spectrum dominates the whole spectrum, the temperature and density can be estimated for the entire duration of the expansion of the plume. The plasma electron temperature is obtained from singly ionized Sn emission lines by the Boltzmann plot method, while the electron density measurements are made using the Stark broadening method.[23] Figure 10 shows the temporal evolution of electron temperature and density for both plasmas. It is observed that the electron density and electron temperature have the maximum values at the delay of 73 ns, which might be due to that the absorbed energy is converted into the internal energy of the plasma and the intensities of the lines are strong over this period. For the Sn plasma, the measured electron temperature and density decrease from 18.7 eV to 1.78 eV and from 9.66×1017 cm−3 to 2.63×1017 cm−3, respectively, as the delay time increases from 73 ns to 143 ns. For the SnO2 plasma, the measured electron temperature and density decrease from 20.4 eV to 1.87 eV and from 17.4×1017 cm−3 to 2.8×1017 cm−3, respectively, when the delay time increases from 73 ns to 143 ns.

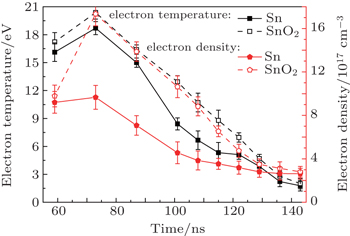Fig. 10. Temporal variation of the electron temperature and density of both plasmas produced by Nd:YAG laser of 216 mJ at 10−3 Pa.

Moreover, the impacts of the vacuum degree on the plasma parameters are investigated. Figure 11 shows the maxima of electron temperature and density of both plasmas at the pressure ranging from 10−3 Pa to 10 Pa with the incident laser energy of 216 mJ. In general, the electron temperature decreases with the pressure increasing. At the pressure of 10−3 Pa, the highest temperature (up to 43 eV) is obtained. We compare the pressure effects on the electron density; it is found that the initial rising trend is quite similar for all circumstances. The enhancement in electron density and temperature at higher pressure can be explained as follows: the shielding effect and the confinement of plasma by the background gas are dominated at higher pressure, resulting in an increase in energy gain in plasma from the incident laser pulse and the chance of the electron–ion collision increased. Therefore at higher pressures, denser and hotter plasmas with high temperature and high electron density are observed. Under identical experimental conditions, the plasma parameters of Sn are lower than those of SnO2. These results in the electron temperature may be attributed to the power absorbed by the expanding plasma from the incident laser pulse. The difference of SnO2 and Sn plasma electron densities may be attributed to the ion density.

Fig. 11. Variation of electron temperature and density with vacuum degree. The incident laser pulse energy is 216 mJ.

The electron temperature and electron density are considered to be two of the most important parameters of plasma, as other parameters are highly dependent on them. So we also investigate the effect of the laser pulse energy on the electron temperature and density of both plasmas. The laser energy can be changed from 50 mJ to 216 mJ by adjusting the quartz attenuation. Figure 12 shows the resulting variation in the maximum electron temperature and density with different incident laser pulse energies at a pressure of 10−3 Pa. It is observed that both plasma parameters are increased with increasing laser pulse energy. This is because the incident laser pulse can provide more energy to plasma when its energy is higher. With increasing laser pulse energy, more excited species, ions, and free electrons are generated that interact with the incoming laser photon, leading to further heating and ionization and resulting in an increase in the absorption of the laser energy. The plasma parameters (electron temperature and electron density) are 7.88 eV and 9.98 × 1017 cm−3 with the laser pulse energy of 130 mJ for the SnO2 plasma, whereas they are 6.15 eV and 4.23 × 1017 cm−3 for the Sn plasma. The plasma parameters of the SnO2 plasma are higher than those of the Sn plasma. These results may be attributed to the power absorbed by the expanding plasma from the incident laser pulse.

Fig. 12. Variation of maximum electron temperature and density with incident laser pulse energy. The pressure in the chamber is 10−3 Pa.
4. Conclusion

We have conducted a comprehensive comparison of EUV emission, plume expansion, ion debris features, and optical spectrum of Nd:YAG laser produced metal Sn and ceramic SnO2 plasmas under identical experimental conditions. Moreover, the influence of the vacuum degree on both plasmas has been studied in the experiment.

The EUV spectra of Sn and SnO2 plasmas possess similar line structures with the peak emission occurring at about 13.5 nm, and a narrower spectral bandwidth is obtained from the ceramic SnO2 target compared to that from the pure Sn metal target. The intensity of the EUV spectrum decreases with increasing background gas pressure. For fixed laser pulse energy and pressure, the EUV radiation from the ceramic SnO2 target is lower than that from the metal Sn target, which is primarily due to the low density of Sn ions. The Sn plasma reaches a peak CE of 1.03%, the peak SnO2 CE is 0.69%, both at the pressure of 10−3 Pa, and both EUV CEs decrease with the increase of the gas pressure.

The hydrodynamic expansion features of the plasma plume under different vacuum degrees are investigated using ICCD imaging fast photography. The wave front boundaries and shapes of the plasma plumes are differet. Under the same delay and pressure, the SnO2 ion plasma plume has a much broader ion profile and an increased boundary distance compared to those of the Sn plasma plume. The calculation results show that the kinetic energies of both plasmas decrease with increasing background gas pressure and the ion kinetic energy of the SnO2 plasma is higher than that of the Sn plasma under the same pressure.

The total number of ions emitted from the SnO2 plasma is larger than that from the Sn plasma. The peak ion kinetic energies and ion fluxes of the Sn and SnO2 plasmas are observed to be dependent on the gas pressure, and display an exponentially saturating trend. The SnO2 plasma is found to have a larger kinetic energy and, as a result, larger ion debris when compared with the Sn plasma. The SnO2 plasma has been found to be more damaging to multilayer mirrors (MLMs) due to the higher peak KEs and greater ion fluences.

The optical emissions generated by the Nd:YAG laser with Sn and SnO2 have also been investigated using time-resolved OES measurements. Under the identical experiment condition, the emission lines of the SnO2 plasma are much stronger than those of the Sn plasma, which depend on the thermodynamic properties of the target material. The temporal variations of the plasma parameters (electron temperature and density) have also been investigated. It is observed that the electron temperature and density of the SnO2 plasma are higher than those of the Sn plasma. The difference in the SnO2 and Sn plasma temperatures may result from the power absorbed by the expanding plasma, and the ion density depends on the electron density of the plasma. Furthermore, strong enhancements of the plasma parameters with increasing pressure are observed. As the vacuum degree increases, the electron density and electron temperature increase. Furthermore, the effect of the laser pulse energy on the plasma parameters has also been investigated. The results show that the electron temperature and density of both plasmas increase with the increase of the laser pulse energy. Under the identical experiment condition, the plasma parameters of the SnO2 plasma are higher than those of the Sn plasma because of more energy being absorbed from the higher incident laser pulse.

In conclusion, both the total amount of ions and the kinetic energy are higher in the SnO2 plasma, while the EUV conversion efficiency is lower, compared with the Sn plasma.

Reference
1Bakshi V2006EUV Sources for LithographyNewYorkSPIE Press
2Dou Y PSun C KLiu C Z 2014 Chin. Phys. B 23 075202
3Liu T HHao Z QGao XLiu Z HLin J Q 2014 Chin. Phys. B 23 085203
4Chen HLan HChen Z QLiu L NWu TZuo D LLu P XWang X B 2015 Acta Phys. Sin. 64 075202 (in Chinese)
5Wu TWang X BWang S Y 2012 J. Appl. Phys. 111 063304
6LiuY FZhang L SHe W L 2015 Acta Phys. Sin. 64 045202 (in Chinese)
7Tanaka HAkinaga KTakahashi AOkada T2004Proc. SPIE5662313
8Bowering NMartins MPartlo W NFomenkov I V 2004 J. Appl. Phys. 95 16
9Coons R WCampos DCrank MHarilal S SHassanein A 2010 Proc. SPIE 7636 763636
10Nagano AInoue TNica P EAmano SMiyamoto SMochizuki T 2007 Appl. Phys. Lett. 90 151502
11Ueno YAriga TSoumagne GHigashiguchi TKubodera SPogorelsky IPavlishin IStolyarov DBabzien MKusche KYakimenko V 2007 Appl. Phys. Lett. 90 191503
12George S ASilfvast W TTakenoshita KBernath R TKoay C SShimkaveg GRichardson M C 2007 Opt. Lett. 32 997
13Choi H WDaido HYamagami SNagai KNorimatsu TTakabe HSuzuki MNakayama TMatsui T2002J. Opt. Soc. Am. B171616
14Hayden PSheridan PO'Sullivan GDunne P AGaynor LMurphy N2005Proc. SPIE5826154
15Xin J G2013The Journal of Macro Trends in Technology and Innovation11
16Tao YSohbatzadeh FNishimura HMatsui RHibino TOkuno TFujioka SNagai KNorimatsu TNishihara KMiyanaga NIzawa YSunahara AKawamura T 2004 Appl. Phys. Lett. 85 1919
17O'Sullivan GFaulkner R 1994 Optical Engineering 33 3978
18Cai Y Wang W TYang MLiu J S Lu P XLi R XXu Z Z2008Acta Phys. Sin575100(in Chinese)
19Takahashi ANakamura DTamaru KAkiyama TOkada T 2008 Appl. Phys. B 92 73
20Amano SInoue THarada T 2011 Appl. Opt. 52 16
21Verbraak HKüpper FJonkers JBergmann K 2010 J. Appl. Phys. 108 093304
22http://physics.nist.gov/PhysRefData/Handbook/Tables/tintable4.htm
23Griem H R1963Phys. Rev.1311170