Cite this Article
Xu Xin, Hu Xiaohong, Feng Ye, Liu Yuanshan, Zhang Wei, Yang Zhi, Zhao Wei, Wang Yishan. Theoretical analysis of the electromagnetic field inside an anomalous-dispersion microresonator under synthetical pump. Chinese Physics B, 2016, 25(3): 034208  
Permissions
Theoretical analysis of the electromagnetic field inside an anomalous-dispersion microresonator under synthetical pump
Xu Xin1, 2, Hu Xiaohong1, 2, Feng Ye1, 2, Liu Yuanshan1, †, , Zhang Wei1, Yang Zhi1, Zhao Wei1, Wang Yishan1, ‡,
State Key Laboratory of Transient Optics and Photonics, Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China
University of Chinese Academy of Sciences, Beijing 100049, China

 

† Corresponding author. E-mail: liuyuanshan@opt.ac.cn

‡ Corresponding author. E-mail: yshwang@opt.ac.cn

Project supported by the National Major Scientific Instrumentation Development Program of China (Grant No. 2011YQ120022), CAS/SAFEA International Partnership Program for Creative Research Teams, China, and the National Natural Science Foundation of China (Grant No. 61275164).

Abstract
Abstract

We study the spatiotemporal evolution of the electromagnetic field inside a microresonator showing an anomalous dispersion at the pump wavelength by using the normalized Lugiato–Lefever equation. Unlike the traditional single continuous wave (CW) pumping, an additional pump source consisting of periodical pulse train with variable repetition rate is adopted. The influences of the microresonator properties and the pump parameters on the field evolution and the electromagnetic field profile are analyzed. The simulation results indicate that, in the anomalous dispersion regime, both increases of the input pulse amplitude and the repetition frequency can result in the field profiles consisting of multiple peaks. A series of equidistant pulses can also be obtained by increasing the CW pump power. In addition, we find that a large physical detuning between the pump laser carrier and the cavity resonance frequency also causes the splitting of the inside field.

PACS: 42.65.−k;42.65.Re;42.81.Wg;
Keyword:microcavity;nonlinear optics;Lugiato–Lefever equation;field evolution;
1. Introduction

The optical frequency combs are the indispensable tools for various applications, e.g., precision frequency metrology, absolute distance measurement, arbitrary waveform generation, accurate optical clocks, etc.[1–4] To date, in the practical applications, the realization of frequency combs is mainly founded on the mode-locked fiber lasers because of their robustness and reliable merits.[5–7] However, some drawbacks still exist for such kinds of frequency combs. For example, the mode spacing denoted by the repetition frequency of periodical pulse trains is restricted by the cavity length of the fiber laser. The largest mode spacing obtained to date is about several GHz.[8,9] Fortunately, the optical Kerr frequency combs generated from microresonator cavities with ultrahigh quality factors were reported a few years ago.[10–12] The mode spacing of the Kerr combs can be tens or hundreds of GHz,[13,14] even up to 1 THz,[15] which is much larger than that of the traditional frequency combs. Moreover, in addition to the large mode spacing, the Kerr combs also show the advantages of simplicity, small size, high degree of integration, and low power consumption.[16,17] Therefore, as the supplement for the traditional mode-locked laser-based frequency combs, the Kerr combs with high repetition frequencies are desirable for many applications, for example, calibration of astronomical spectrograph[18] and coherent terabit communications.[19]

Meanwhile, the generation of the optical Kerr frequency combs has also been studied theoretically. At first, the modal-expansion approach was employed to explain the generation mechanisms of the Kerr combs.[20,21] But it cannot be applied when numerous modes coexist in the microresonator.[22] In recent years, a modified model based on the well-known Lugiato–Lefever equation (LLE) is established. In this spatiotemporal Lugiato–Lefever formalism, the diffraction item is replaced by the azimuthal dependence of the intracavity field. With the aid of this formalism, the evolution of the laser field in a microresonator can be analyzed, even though there are a great number of modes interacting with each other in the cavity.[23] Furthermore, it was reported that the simulation results by using the LLE show good agreement with the experimental results.[24] To the best of our knowledge, the theoretical analysis of the Kerr combs based on the LLE is confined to the continuous wave (CW) pump cases. Moreover, the central wavelength of the pump source is selected to lie in the anomalous dispersion region of the microresonator. Compared with the normal dispersion region, in this case, a wideband Kerr frequency comb can be easily realized as shown by both experimental and theoretical studies.[25–27]

In this work, based on the normalized LLE, the spatiotemporal dynamics of the electromagnetic field in a microresonator with an anomalous dispersion is investigated. Unlike the traditional CW pumping case, the microresonator cavity is pumped by the combination of CW and periodical pulse train sources. The dependence of various electromagnetic field evolutions on the cavity detuning and the pump source parameters is carefully investigated. All these parameters are experimentally tunable. The calculation results show that both the increases in pump pulse amplitude and repetition frequency result in multiple peaks in the intensity profile. In addition, it is found that, in the anomalous dispersion regime, a series of equidistant pulses can be generated by raising the CW pump power. Chaos occurs with further increase of the pump power. Meanwhile, the analysis results show that large pump detuning is unfavorable for the generation of stable Kerr frequency combs.

2. Theoretical model

The schematic diagram of the Kerr frequency comb generation system based on the combination of a tapered optical fiber and a microresonator is shown in Fig. 1. The coupling of pump light into the resonator cavity can be realized by tapering the single mode fiber and using the evanescent field around the taper waist.

Fig. 1. Schematic representation of Kerr frequency comb generation system.

Referring to the existing work, the model describing a microresonator pumped by a CW laser is introduced as follows. It is supposed that the laser propagates along a straight track in the microresonator with periodic boundary conditions.[28,29] In this case, the variant of LLE named spatiotemporal Lugiato–Lefever formalism is found suitable for describing the evolution of the field inside the microresonator cavity.[30–32] The normalized LLE can be written as

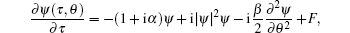
where ψ(τ, θ) is the complex field envelope, θ ∈ [−π, π] is the azimuthal angle along the circumference of the microresonator, τ = t/2τph is the rescaled dimensionless propagation time with τph = 1/Δwtot being the photon lifetime, the parameter Δwtot = w0/Qtot denotes the mode bandwidth, and Qtot is the loaded quality factor. The parameter α = −2(Ω − w0)/Δwtot is the frequency detuning between the pump laser carrier frequency Ω and the cold cavity resonance frequency w0. The parameter β stands for the second-order dispersion of the microresonator, and the external CW pump power is proportional to F2. The first term on the right-hand side of the LLE represents the loss of the microresonator.

For solving the LLE, the condition of ∂ ψ(τ, θ)/∂ τ = 0 is set and the corresponding steady-state solutions of the electromagnetic field in the cavity can be acquired by using the multi-dimensional Newton–Rhapson root-finding method.[24] However, the transient dynamics during comb formation are still unclear when this method is used. Therefore, instead, the split-step Fourier algorithm is utilized to discuss the evolution characteristics of the Kerr optical frequency combs.[33]

The field evolution in the microresonator pumped by a CW laser together with a periodic pulse source can be discussed by solving the LLE above. Here, a microresonator parameter named free spectral range (FSR) is introduced and it is defined as FSR = 1/tR, where tR is the roundtrip time of the laser inside the microresonator. The input periodical pulses are assumed to be produced by mode-locked lasers and the repetition frequency is denoted by f = FSR/m, where m is an arbitrary integer. Moreover, it is assumed that the center wavelength of the pump pulses is the same as that of the CW pump. Considering that the length of the tapered fiber is extremely short, the interaction between the pulses and the CW laser in the tapered fiber can be ignored. Thus, they propagate independently before entering into the microresonator cavity. In the interval between two consecutive input pulses, the field profile in the microresonator still follows the LLE. When the periodical pulses are imported into the microresonator, it is regarded that the input pulse field is added to the original field in the microresonator. Based on the above assumptions, the electromagnetic field produced by the synthetical pump is simulated by using the normalized LLE.

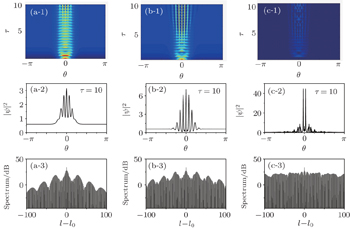
3. Theoretical analysis of the field evolution with synthetical pump
3.1. Kerr frequency comb generation with synthetical pump

In this section, the evolution of the field inside the microresonator with anomalous dispersion is discussed. Bright solitons can form in the nonlinear optical cavity under the balance of nonlinearity and dispersion. This balance process mainly affects the soliton shape, and the amplitude of the soliton is determined by the balance between gain and dissipation. In particular, the initial pattern formation in the microresonator is caused by the modulation instability (MI) effect.[34,35] According to Ref. [34], the initial field envelope is set as a Gaussian function: ψ0 = 0.5 + 0.5exp[−(θ/0.5)2]. It has been reported that a soliton is generated when the cavity detuning in the case of anomalous dispersion.[36] Our simulation also shows that when the , the initial Gaussian pulse evolves into a constant pattern with the help of the CW pump. Therefore, Kerr frequency combs cannot be realized. To generate the Kerr frequency combs, the CW pump and the periodical pump pulses are then imported simultaneously. Under the condition of α = 0.5, the evolution of the field profile in the microresonator with time parameter τ corresponding to combs generation cases is demonstrated in Fig. 2(a). It is noted that the second-order or group velocity dispersion parameter β is negative and designated as β = −0.01. With the synthetical pump manner, the field in the microresonator varies periodically. The pulse shapes and the corresponding spectra at different moments in a period are shown in Fig. 2(b). At τ = 8.4, even though two symmetrical shoulders appear, the Kerr frequency combs can still be generated and the spectral profile is almost not affected.

Fig. 2. (a) Spatiotemporal evolution of the field in the microresonator with anomalous dispersion. The parameters are α = 0.5, β = −0.01, F = 0.8 and the initial field in the microresonator is ψ0 = 0.5 + 0.5exp[−(θ/0.5)2]. The field of the input pump pulses is ψim = 0.5exp [−(θ/0.5)2], and the repetition frequency is set as f = FSR/500. (b) Several intensity profiles and the corresponding spectra of the fields at different moments in a variation period.
3.2. Influence of the pump characters on the field

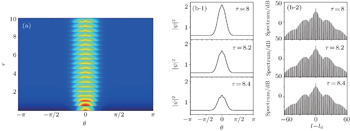
We carefully study the effects of the pump pulse parameters on the field profile in the microresonator. In order to make comparison with the results shown in Fig. 2, only the amplitude of the input pump pulses is varied, and the field profiles at τ = 10 are displayed in Fig. 3. In Fig. 3(a), for a pump pulse profile of ψin = exp[−(θ/0.5)2], the field intensity profile shows 5 peaks. The result is different from the CW pump case where bright cavity soliton or multiple-soliton molecules can be formed from an initial field with a Gaussian profile in the subcritical bifurcation case.[37] The Kerr frequency combs can also be observed and show a similar profile to that of the soliton molecules. Explicitly, an evident slow modulation is exhibited in the spectrum. When the amplitude of the pump pulses is increased to 1.5, seven peaks are observed in the field profile, as shown in Fig. 3(b). However, when the amplitude is further increased to a larger value, the stable profile of the electromagnetic field cannot be maintained owing to the strong nonlinear effect, as shown in Fig. 3(c). The field evolves into some sharps without regular pattern. It can be explained by the strong nonlinear effect because of the high peak power in the microresonator. Next, the influence of the repetition frequency of the pump pulse train on the field evolution is investigated, as shown in Fig. 4. With the repetition frequency increasing, the input pulses coupled into the microresonator at different time may overlap with each other. The superposition of multiple pulses leads to the powerful peak, which is the premise of the nonlinear effect. Therefore, the field in the microresonator evolves into multiple peaks, as Fig. 4(b) shows. The further increase of the pump pulse repetition frequency will eventually result in an irregular pattern of the field intensity profile, as shown in Fig. 4(c).

Fig. 3. Spatiotemporal evolution of the field in the microresonator with different amplitudes of the pump pulses, the field profiles at τ = 10, and the corresponding spectra: (a) ψin = exp[−(θ/0.5)2], (b) ψin = 1.5exp[−(θ/0.5)2], (c) ψin = 2exp[−(θ/0.5)2].
Fig. 4. Spatiotemporal evolution of the field in the microresonator with different pump pulse repetition frequencies: (a) f = FSR/1000, (b) f = FSR/200, (c) f = FSR/100. The profile of the pump pulse is set as ψin = 0.5exp[−(θ/0.5)2].

In addition, the power of the external CW pump, which is proportional to F2, also plays an important role in the microcavity optical field evolution. The field evolution and the intensity profiles corresponding to different pump parameters F are displayed in Fig. 5. The other parameters are the same as those used in Fig. 2. Figures 5(a) and 5(b) show that, for a large pump parameter F (e.g., F = 1.4), the pulse splits into a series of equidistant pulses gradually, which form a stable distribution ultimately. It is interesting to note that, in Fig. 5(a), the peaks of the spectrum are separated by 21 FSR, which is equal to the number of the peaks in the field intensity profile. At a higher pump (e.g., F = 2.5), the initial field evolves into a disordered profile, which is well known as the chaos. The chaos can generate in any nonlinear system with at least three degrees of freedom. According to Ref. [36], one route to chaos generation corresponds to unstable turning patterns and can be practically realized by increasing the pump strength. Physically, the chaos realized in this case is a consequence of bifurcations starting with unstable primary combs and the following generation of secondary, even higher-order combs. This process terminates until a totally chaotic state is reached. In addition, the chaos also relates to the unstable solitons. With the increase of pump parameter F, the field in the microresonator becomes unstable and evolves into a regime which is characterized by the irregular pattern of powerful peaks. The situation can arise in a very wide variety of nonlinear physical systems. Meanwhile, the chaos exists in the microresonator all the time.

Fig. 5. Spatiotemporal evolution of the field in the microresonator and the corresponding spectra under different CW pump powers: (a) F = 1.4, (b) F = 1.9, (c) F = 2.5. The field profile of the pump pulse is ψin = 0.5exp[−(θ/0.5)2].
3.3. Influence of the microresonator character on the field

We further investigate the effect of the frequency detuning on the field evolution in the microresonator. The field evolution under different frequency detuning is displayed in Fig. 6. As shown in the figure, the input pulse splits and more peaks form inside the microresonator when the frequency detuning increases. At even larger frequency detuning, the stable field cannot be sustained and no regular pattern is formed. It can be understood by noting that a large frequency detuning α leads to a mismatch between the pump laser carrier frequency and the cold cavity resonance frequency. The result of this large frequency mismatch is a pulse splitting, even the generation of an irregular field profile. Therefore, to avoid the above processes, the frequency detuning should be reduced as much as possible in practice.

Fig. 6. Spatiotemporal evolution of the field in the microresonator with different physical detunings: (a) α = 0.8, (b) α = 1.5, (c) α = 2.5.
4. Conclusion

The spatiotemporal evolution of the electromagnetic field inside a microresonator with an anomalous dispersion is investigated. The cavity is pumped by the combination of CW and pulsed sources. Based on the normalized LLE and the split-step Fourier algorithm, the transient dynamics at different time during comb formation in the microresonator cavity are carefully studied. In the anomalous dispersion regime, both high amplitude and high repetition frequency of the pump pulse can result in multiple peaks in the field intensity profile. With the increase of the CW pump power, the field can evolve into a series of equidistant pulses and eventually into a chaos state. In addition, a large physical detuning can also result in the splitting of the input field and the occurrence of multiple peaks in the intensity profile. The theoretical analysis results obtained in this paper are crucial and helpful for the practical applications. According to the simulation results, the material of the microresonator and the pump parameters can be optimized for the Kerr frequency comb generation.

Reference
1Yasui TYokoyama SInaba HMinoshima KNagatsuma TAraki T 2011 IEEE J. Sel. Topics Quantum Electron 17 191
2Coddington ISwann W CNenadovic LNewbury N R 2009 Nat. Photon. 3 351
3Cundiff S TWeiner A M 2010 Nat. Photon. 4 760
4Diddams S A 2010 J. Opt. Soc. Am. B 27 B51
5Washburn B RFox R WNewbury N RNicholson J WFeder KWestbrook P SJørgensen C G 2004 Opt. Express 12 4999
6Washburn B RDiddams S ANewbury N RNicholson J WYan M FJørgensen C G 2004 Opt. Lett. 29 250
7Swann W CMcFerran J JCoddingtonNewbury N RHartl IFermann M EWestbrook P SNicholson J WFeder K SFejer M M 2006 Opt. Lett. 31 3046
8McFerran J JNenadović LSwann W CSchlager J BNewbury N R 2007 Opt. Express 15 13155
9Byun HSander M YMotamedi AShen HPetrich G SKolodziejski L AIppen E PKärtner F X 2010 Appl. Opt. 49 5577
10Herr THartinger KRiemensberger JWang C YGavartin EHolzwarth RGorodetsky M LKippenberg T J2011Nat. Photon.241
11Kippenberg T JSpillane S MVahala K J 2004 Appl. Phys. Lett. 85 6113
12Vahala K J 2003 Nature 424 839
13Saha KOkawachi YShim BLevy J SSalem RJohnson A RFoster M ALamont M R ELipson MGaeta A L 2013 Opt. Express 21 1335
14Del’Haye PArcizet OSchliesser AHolzwarth RKippenberg T J 2008 Phys. Rev. Lett. 101 053903
15Kippenberg T JHolzwarth RDiddams S A 2011 Science 332 555
16Cao SXu X L 2014 Physics 43 740
17Li C F2012Physics41635
18Steinmetz TWilken THauck C AHolzwarth RHänsch T WPasquini LManescau AD’Odorico SMurphy M TKentischer TSchmidt WUdem T 2008 Science 321 1335
19Pfeifle JBrasch VLauermann MYu YWegner DHerr THartinger KSchindler PLi JHillerkuss DSchmogrow RWeimann CHolzwarth RFreude WLeuthold JKippenberg T JKoos C2013Nat. Photon.8375
20Savchenkov A AMatsko A BStrekalov DMohageg MIlchenko V SMaleki L2005Phys. Rev. Lett.93243905
21Chembo Y KStrekalov D VYu N 2010 Phys. Rev. Lett. 104 103902
22Chembo Y KYu N 2010 Phys. Rev. A 82 033801
23Lamont M R EOkawachi YGaeta A L 2013 Opt. Lett. 38 3478
24Coen SRandle H GSylvestre TErkintalo M 2013 Opt. Lett. 38 37
25Herr TBrasch VJost J DWang C YKondratiev N MGorodetsky M LKippenberg T J 2013 Nat. Photon. 8 145
26Del’Haye PSchliesser AArcizet OWilken THolzwarth RKippenberg T J 2007 Nature 450 1214
27Razzari LDuchesne DFerrera MMorandotti RChu SLittle B EMoss D J 2010 Nat. Photon. 4 41
28Matsko A BSavchenkov A ALiang WIlchenko V SSeidel DMaleki L 2011 Opt. Lett. 36 2845
29Agha I HOkawachi YGaeta A L 2009 Opt. Express 17 16209
30Lugiato L ALefever R1987Phys. Rev. Lett.252209
31Coen SErkintalo M 2013 Opt. Lett. 38 1790
32Parra-Rivas PGomila DMatias M ACoen SGelens L 2014 Phys. Rev. A 89 043813
33Chembo Y KMenyuk C R 2013 Phys. Rev. A 87 053852
34Coen SHaelterman M 2001 Opt. Lett. 26 39
35Hansson TModotto DWabnitz S 2013 Phys. Rev. A 88 023819
36Leo FGelens LEmplit PHaelterman MCoen S 2013 Opt. Express 21 9180
37Godey CBalakireva I VCoillet AChembo Y K 2014 Phys. Rev. A 89 063814