† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 21373270 and 11504431) and the Fundamental Research Funds for Central Universities of China (Grant No. 15CX02025A).
Under appropriate physicochemical conditions, short peptide fragments and their synthetic mimics have been shown to form elongated cross- β nanostructures through self-assembly. The self-assembly process and the resultant peptide nanostructures are not only related to neurodegenerative diseases but also provide inspiration for the development of novel bionanomaterials. Both experimental and theoretical studies on peptide self-assembly have shown that the self-assembly process spans multiple time and length scales and is hierarchical. β -sheet self-assembly consists of three sub-processes from the microscopic to the mesoscopic level: β -sheet locking, lateral stacking, and morphological transformation. Detailed atomistic simulation studies have provided insight into the early stages of peptide nanostructure formation and the interplay between different non-covalent interactions at the microscopic level. This review gives a brief introduction of the hierarchical peptide self-assembly process and focuses on the roles of various non-covalent interactions in the sub-processes based on recent simulation, experimental, and theoretical studies.
Peptide self-assembly is a process where peptides spontaneously form ordered supramolecular structures from the bottom-up, driven by non-covalent interactions. When peptides undergo self-assembly to form insoluble fibrillar aggregates in the brain, neurodegenerative diseases such as Alzheimer’s, Huntington’s, and Parkinson’s are often caused. [ 1 – 4 ] Although the type of peptides involved in these diseases varies significantly in amino acid composition and sequence, there exist similarities in the morphologies and structures they form, i.e., fibrils with cross- β structures. Clarifying the mechanisms underlying their formation is critical for circumventing and treating these associated diseases. Furthermore, the relevant peptides and fragments, as well as their synthetic mimics, have been shown to form a variety of ordered nanostructures in vitro , such as twisted and helical ribbons, nanotubes, and nanobelts, in addition to fibrils. [ 5 – 13 ] These peptide nanostructures show great promise in the development of novel nanomaterials for biomedical and technological applications because of their unique biological functions and physiochemical properties. [ 14 – 16 ]
The self-assembled nanostructures are dictated by the balance between attractive and repulsive interactions, such as van der Waals, electrostatic, hydrophobic, π – π stacking, and hydrogen bonding interactions. The hierarchical process and the resulting nanostructures change when this balance is disturbed. The main strategies utilized to tune the balance include changing the peptide sequences [ 17 – 19 ] and solution conditions (e.g., pH, ionic strength, and organic solvent addition). [ 20 – 25 ] In addition, the self-assembly process of elongated ordered aggregates with cross- β structures from peptides is hierarchical and spans multiple time and length scales, which has been demonstrated in both experimental and theoretical studies. [ 26 – 29 ] Three distinctive sub-processes occur during the hierarchical process from the microscopic to the mesoscopic level— β -sheet locking, lateral stacking, and morphological transformation (Fig.
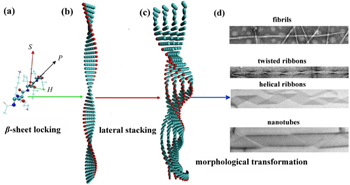 | Fig. 1. Sub-processes in the hierarchical self-assembly of β -sheet peptides: β -sheet locking along the hydrogen bonding direction (the long axis growth), which is responsible for the elongation of assemblies, lateral stacking of β -sheets along the side chain direction for the width growth, and morphological transformation of assemblies with different widths. { H , S , P } is the local coordinate of the peptide, where H is the hydrogen bonding direction, S is the side chain direction, and P is the backbone direction from the N-terminus to the C-terminus. [ 30 ] |
Through experimental and computational studies, β -sheet hydrogen bonding between neighboring peptide backbones has been confirmed to be the initial event and then responsible for the elongation of assemblies to form various 1D nanostructures. The β -sheet conformations can be determined by using the circular dichroism (CD) and Fourier transform infrared (FTIR) spectroscopy techniques, in which characteristic CD peaks at approximately 195 nm and 218 nm and an FTIR peak at approximately 1624 cm –1 are readily observed for β -sheets. Using fiber x-ray diffraction (XRD) and nuclear magnetic resonance (NMR), the structures of cross- β sheets were further characterized at the microscopic level, including determination of the distance between neighboring backbones and the packing modes (e.g., the antiparallel and parallel arrangement and the residue registry). [ 31 , 32 ] For example, x-ray diffraction characterization revealed an identical distance of 4.8 Å between the neighboring backbones of cross- β peptide fibrils, irrespective of the different peptide sequences. [ 13 , 33 , 34 ] Using all-atomistic computer simulations, additional detailed structural information of cross- β sheets has been deduced at the microscopic level, such as the residue registry and the twisting angle between neighboring backbones. [ 35 – 37 ]
Peptides containing residues with high hydrophobicity and a strong β -sheet forming propensity tend to pack into β -sheets. Comparing I 3 K with L 3 K, the former self-assembles into tubular fibrils with a β -sheet conformation while the latter forms spherical aggregates with random coils, as a result of the stronger β -sheet forming propensity of isoleucine relative to that of leucine. [ 38 ] By systematically investigating the effect of the side chain hydrophobicity on the critical coagulation concentration of ( X K X E) 3 , where X denotes F, I, and V, respectively, Caplan et al. found that increasing the side chain hydrophobicity decreased the critical coagulation concentration by increasing the driving force for assembly. [ 39 ] For hydrophilic residues, the charged state and pattern along the backbone significantly affect the packing mode of backbones within β -sheets. Mehta et al. observed different self-assembled 1D nanostructures of short A β (16–22), which is a hydrophobic core fragment of the amyloid- β peptide from residues 16 to 22, at pH 2 and pH 6 to be nanofibers and nanotubes, respectively. Based on the results of studies combining NMR and isotope-editing FTIR, Mehta et al. suggested an in-register antiparallel packing mode for the nanofibers and an out-of-register antiparallel packing mode (one-residue shift) for the nanotubes. [ 21 ] In our recent studies, we also observed and simulated the effect of the distribution of charged residues along the backbone on the packing modes of backbones and the final self-assembled nanostructures. [ 37 , 40 ] As shown in Fig.
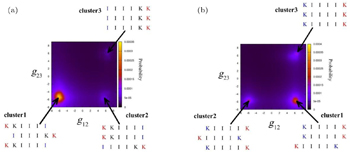 | Fig. 2. Free energy landscapes for IIIIKK and KIIIIK were calculated by all atomistic replica exchange molecular dynamics simulation. The X axis is the contact degree g 12 between peptide1 and peptide2 and the Y axis is the contact degree g 23 between peptide2 and peptide3, where the peptides in the trimer have been reordered. [ 36 ] |
Using experimental methods alone, it is generally difficult to observe directly the packing dynamics and elongation process of β -sheets at the microscopic level. In theoretical and computational studies, a two-step dock-and-lock elongation mechanism for peptide self-assembly has been proposed. [ 41 – 43 ] In this mechanism, the monomer in a partially structured state docks with the fibril end, and then the monomer undergoes structural reorganization to lock itself to the fibril as a β -sheet structure. [ 44 ] To quantify the docking process, theoretical work has used diffusion-limited aggregation kinetics to study the association rate constant, in which the concentration of the monomer was considered to be the only factor significantly affecting this process. [ 45 ] From theoretical and simulation studies of A β peptides and their congeners in aqueous solution, however, the monomeric conformation of the peptides was found to have a large hydrophobic surface area, suggesting that hydrophobic interactions play an essential role in the docking process of peptide self-assembly. [ 46 – 48 ] By conducting extensive molecular dynamics simulations of peptide aggregation in explicit water, Thirumalai et al. directly observed the locking process following monomer docking at the end of fibrils. [ 49 , 50 ] They found that the β -strand content of the monomer showed a sharp transition from 0.65 for the initial docking state to 0.8 for the final locking state and that the hydrogen bonding interactions between backbones stabilized the ordered structure in the locking state.
Following hydrogen bonding between backbones and the dock-and-lock process, the resultant sheets undergo lateral stacking along the side chain direction. In early studies of fibrillarstructures formed by A β peptides with different lengths, laminated structures with different cross- β sheet numbers have been reported. [ 51 , 52 ] Using transmission electron microscopy (TEM), small angle neutron scattering (SANS), and small angle x-ray scattering (SAXS), Lu et al. evaluated the structure of nanotubes formed by A β (16–22) at pH 2, and demonstrated that nanotubes also arose from the lamination of twisted cross- β sheets. [ 53 ] The laminated character of the β -sheet for peptide nanostructures has been consolidated by Eisenberg et al. through systematic study of the supramolecular structures formed by various peptides. [ 31 , 32 ] In addition, based on the atomic-level structures resolved in their work, they classified the types of lateral stacking according to the two criteria. One is whether sheets pack with the same or different surfaces adjacent to one another, while the other is whether the sheets are oriented parallel or antiparallel with respect to one another. Combining types of packing modes in cross- β sheets with the lateral stacking modes on the atomic level, Eisenberg et al. proposed eight different elementary structures as the common structures for supramolecular structures formed by different β -sheet peptides. [ 32 ]
Similarly to the packing of backbones, the lateral stacking of β -sheets is also affected by the amino acid sequence of peptides, [ 51 , 52 ] leading to nanostructures with different widths. Because lateral stacking occurs along the side chain direction, the interactions between side chains of neighboring cross- β sheets dominate this process. In order to understand the effect of the side chain at the microscopic level, many studies have concentrated on developing and studying model peptides. [ 18 , 40 , 54 , 55 ] Experimental and simulation studies on the self-assembly of the hydrophilic polar peptide GNNQQNY confirmed shape complementarity of the side chains as a steric zipper as the main driving force for stabilizing the association of the cross- β sheets. [ 56 , 57 ] In the study of QQRFQWQFQQQ, Aggeli et al. suggested that the hydrophobic interaction between cross- β sheets was the main driving force for their lateral stacking in peptide self-assembly. [ 6 ] The effect of electrostatic interactions is, however, more complex and appears to depend on the distribution of charged residues. For the short peptides KIIIIK and IIIIKK, the charged residues at the two ends of the hydrophobic core could strengthen the degree of lateral stacking by preventing collapse of the hydrophobic core and enhancing the probability of KIIIIK adopting an extended conformation which had a large hydrophobic surface. At the same time, the charged residues at one end cannot prevent collapse of the hydrophobic core of IIIIKK which gave the molecule a small hydrophobic surface relative to KIIIIK. [ 37 , 40 ] In addition, the balance between hydrophobic and electrostatic interactions in peptide self-assembly could be tuned not only by changing the peptide hydrophobicity and sequence, but also by changing the solution conditions such as pH, [ 20 , 21 ] ionic strength, [ 23 , 24 ] and the addition of organic solvents. [ 22 , 25 , 58 ]
Based on the cross- β and lateral stacking structures observed in experiments, Aggeli et al. proposed a hierarchical self-assembly model to understand the different widths of fibrils formed by β -sheet peptides. [ 6 , 26 , 59 ] In this model, there are two kinds of simplified interactions, including the inter-sheet interaction between neighboring cross- β sheets and the intra-sheet interaction between neighboring peptides within a sheet. For simplicity, the inter-sheet interaction is constant and the intra-sheet interaction is modeled by the elastic energy of a deformed sheet. The initial equilibrium structure of a cross- β sheet is a straight twisted conformation. The backbones in neighboring sheets are in parallel in order to decrease the hydrophobic exposure of β -sheets. With this geometric constraint, the outer sheet has a larger deformation and elastic energy penalty. When the elastic energy penalty of the outer sheet is larger than the attractive energy between sheets, fibrils do not grow wider. Based on the competition between the elastic energy penalty of sheets and attraction between neighboring sheets, the physical origin of different widths observed in experiments can be explained. Considering the electrostatic screening effect in this model, the ionic effects on β -sheet peptide self-assembly were successfully used to explain structure changes with changes in ionic concentration. [ 24 , 60 ] Based on the hierarchical model, the different self-assembled morphologies of IIIIKK and KIIIIK have been explained by combining the simulation and experimental results as shown in Fig.
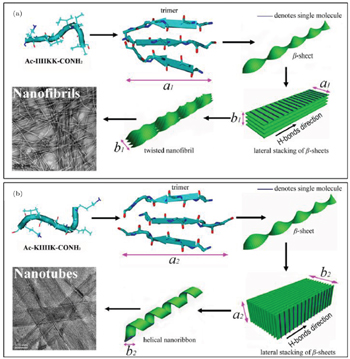 | Fig. 3. Schematic of different morphologies formed by (a) IIIIKK and (b) KIIIIK based on the hierarchical approach. [ 40 ] |
Because the sizes of supramolecular structures formed by β -sheet peptide self-assembly are about 10–1000 nm, their morphologies can be easily observed by using atomic force microscope (AFM) and TEM methods. Accompanying the effect on width growth of the variations in the peptide sequence and solution conditions, different mesoscopic morphologies such as vesicles, fibrils, twisted ribbons, helical ribbons, nanotubes, and nanobelts have been observed in experiments. [ 5 – 13 ] Yan et al. observed that FF could self-assemble to form vesicle-like structures with diameters about 100 nm at low concentrations, but form nanotubes with diameters about 100 nm at high concentrations. [ 61 ] Adamcik et al. observed the untwisting of fibrils formed by β -lactoglobulin with increasing NaCl concentration in solution, [ 24 ] and Castelletto et al. found that two model peptides, AAKLVFF and ( β )A( β )AKLVFF, formed twisted fibers at low NaCl concentrations but large crystal-like nanotapes for AAKLVFF and nanotubes for ( β )A( β )AKLVFF at high NaCl concentrations (( β )A denotes β 2 -alanine residue). [ 23 ] AAKLVFF can form different morphologies at different concentrations of methanol, such as fibrils in solution with low methanol content, nanotapes in solution with 50–70 wt% methanol, and nanotubesin solution with 100 wt% methanol. [ 22 , 58 ] The polymorphism of self-assembled nanostructures formed by peptides is further confirmed by computer simulations. Using the MARTINI [ 62 ] coarse grain model of peptides, Guo et al. found that FF formed various thermal stable structures including vesicles, nanotubes, and planar bilayers based on extensive molecular dynamics simulation. [ 63 ]
Different morphologies formed by the same peptide under different conditions suggest that peptides adopt different metastable or stable states in their self-assembly processes. Unraveling the relationships between these states with different morphologies is a challenging subject for understanding the microscopic mechanism underpinning the formation of different mesocopic morphologies. In a study by Yan et al. , reversible transitions between vesicles and nanotubes were confirmed by observing a necklace-like structure that acted as an intermediate state. [ 61 ] By monitoring self-assembly in real time, many researchers have observed morphological transformation processes prior to the final morphologies formed in experiments. [ 11 , 12 , 64 , 65 ] Pashuck et al. found that the peptide amphiphile C 16 FFFEEE dissolved in water at 10 mM and 25 °C formed short twisted nanotapes at 30 seconds, long twisted nanotapes at 10 minutes, long structures with both twisted and helical features at 2 weeks, and long helical structures at 4 weeks. [ 11 ] Using direct imaging cryo-TEM, the complete path to nanotube formation of another peptide amphiphile, C 12 – β 12 , was observed. [ 64 ] C 12 – β 12 formed thin fibers with widths of less than 10 nm at 10 minutes, twisted ribbons with widths of approximately 20 nm at 24 hours, coiled ribbons with widths of approximately 30 nm at 1 week, unclosed tubes with a diameter of 80 nm at 4 weeks, and closed tubes with a diameter of 80 nm at 4 months. Further, Adamcik et al. observed a similar morphological transformation process by investigating the self-assembly of ( β )A( β )AKLVFF in solution with NaCl. [ 12 ]
The hierarchical model proposed by Aggeli et al. provides a good understanding for the different widths of variouspeptide nanostructures, [ 6 , 26 , 59 ] but cannot explain the morphological transformation process. Although a full understanding of this process has not been achieved, some theoretical studies have been devoted to unravelling the mechanisms and pathways involved in tube formation based on the elasticity theory applied to the self-assembly of chiral molecules. [ 66 – 71 ] According to a multi-lamellar model incorporating the elasticity theory, the phenomenological free energies of morphologies formed by FF in aqueous solution were determined by Yan et al. [ 61 ] In their model, the sphere and cylinder structures were stable under different thermodynamic conditions, and the intermediate state (necklace-like structure) was the metastable structure. By introducing an energy penalty for edges in the elastic strain energy of chiral ribbons, Ghafouri et al. calculated the minimum energy of stripes as a function of width, concluding that there were two stable morphologies for stripes with different widths. One was the twisted ribbon for the small width and the other was helical ribbons for large widths. [ 72 ] The relationship between the morphologies and widths of stripes was also confirmed by Armon et al. [ 73 ] In their study, using the mathematical framework of “incompatible elasticity”, they modeled the stripe structures by two elastic tensors that must fulfill the Gauss–Codazzi–Mainardi equations. The metric tensor contains in-plane stretching deformations, while the curvature tensor contains bending deformations. The quantitative results of the incompatible stripe’s energy showed that the bending energy is proportional to the square of the width, but the stretching energy is proportional to the fourth power of the width. The competition between stretching energy and bending energy determines the morphologies of stripes with different widths. When the width is small, the stable morphology is twisted ribbons, which decrease the elastic energy penalty caused by bending deformation; when the width is large, the stable morphology is helical ribbons, which decrease the elastic energy penalty caused by stretching deformation. By statistically analyzing the correlation between the morphologies and widths observed in peptide self-assembly experiments, Childers et al. confirmed these theoretical conclusions. [ 74 ] They found that when the width of a nanostructure was less than 40 nm, the morphology was twisted ribbon, when the width was between 40 and 100 nm, the morphology was helical ribbon, and when the width was more than 100 nm, the morphology was tubular.
Extensive studies and impressive advances have been made in the field of peptide self-assembly. As described above, peptide self-assembly with β -sheet structures is hierarchical and the microscopic interactions involved have distinct roles in the different sub-processes. β -sheet peptide self-assembly can be divided into three distinct sub-processes β -sheet locking, lateral stacking, and morphological transformation. Hydrophobic interactions drive peptide monomers to dock onto aggregates, and hydrogen bonding interactions between backbones then lock the peptide into the aggregates along the long axis direction. The inter-sheet attraction arising from hydrophobic or electrostatic interactions leads to lateral stacking of cross- β sheets, and competition between the elastic energy penalty of cross- β sheets and inter-sheet attraction leads to different widths of the final nanostructures. With increasing width, the morphology of nanostructures will transform from fibrils to twisted ribbons, then to helical ribbons and finally to nanotubes.
Because β -sheet peptide self-assembly spans multiple time and length scales, various methods based on simulations, experiments, and theories have been utilized to study the underlying mechanisms in peptide self-assembly. The microscopic dynamics of β -sheet elongation have been proposed to follow a two-step dock-and-lock mechanism in all-atomistic simulations, in which the competition mechanism between different interactions and structures at the microscopic level can be well assessed. Through systematic experimental variation of peptide sequences and solution conditions such as pH, ionic strength, and the addition of organic solvents, the cross- β laminated structure has been clearly demonstrated in self-assembled peptide nanostructures. Morphological transformations at the mesoscopic level have also been observed in such systems. Through a combination of elasticity theory on chiral molecule self-assembly and the concepts of cross- β laminated structure, the driving forces in morphological transformation and the physical relationships between widths and morphologies have been demonstrated.
Despite advances in understanding β -sheet peptide self-assembly, it remains difficult to quantitatively assess and mediate self-assembly processes and assembled nanostructures of the cross- β structure. The self-assembly from the microscopic to the mesoscopic level is not completely understood because of the gaps between experimental and theoretical studies. In experiments, it is usually difficult to obtain quantitative information of the microscopic interactions required to build theoretical models with molecular detail. However, the hierarchical viewpoint developed from experiment and theory is a common framework for studying the mechanism of peptide self-assembly. By applying multi-scale computer simulation methods in peptide self-assembly, the strengths of intra-sheet and inter-sheet interactions between peptides involved in β -sheet locking and lateral stacking can be quantitatively studied by atomistic simulations at the microscopic level, and the structures and dynamics of morphological transformations can be quantitatively characterized by coarse grained simulations at the mesoscopic level. The quantitative simulation studies of the sub-processes in peptide self-assembly are keys to bridge the gap between experiment and theory.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 |


