† Corresponding author. E-mail:
Project supported by the Key Project of Scientific and Technological Research in Hebei Province, China (Grant No. ZD2015133).
In terms of Darboux transformation, we have exactly solved the higher-order nonlinear Schrödinger equation that describes the propagation of ultrashort optical pulses in optical fibers. We discuss the modulation instability (MI) process in detail and find that the higher-order term has no effect on the MI condition. Under different conditions, we obtain Kuznetsov–Ma soliton and Akhmediev breather solutions of higher-order nonlinear Schrödinger equation. The former describes the propagation of a bright pulse on a continuous wave background in the presence of higher-order effects and the soliton’s peak position is shifted owing to the presence of a nonvanishing background, while the latter implies the modulation instability process that can be used in practice to produce a train of ultrashort optical soliton pulses.
During the last four decades, optical solitons have been the object of intensive theoretical and experimental studies. [ 1 – 4 ] This is because that optical soliton can be treated as a natural data bit in ultrahigh-speed optical telecommunication systems. [ 5 , 6 ] The all-optical communication link will play the major role in optical fiber transmission systems such as all optical networks, optical communication, and optical logic devices. There are many nonlinear dynamic models in different branches of science which have soliton-like solutions. Based on the balance of the group velocity dispersion and the self-phase modulation, an optical soliton can be formed in fiber. The nonlinear Schrödinger (NLS) equation was reported theoretically by Hasegawa and Tappert [ 1 , 2 ] to describe self-focusing and self-phase modulation of light waves [ 7 – 14 ] in nonlinear optics. The propagation of optical solitons [ 15 – 18 ] are generated by the NLS equation. [ 19 – 21 ] In recent years, the femtosecond optical pulse transmission technology in optical fibers has a rapid development and potential prospect. As early as 1987, the higher-order NLS equation was derived by using the multiple-scale method, [ 11 ] which is the transmission evolution equation of femtosecond optical pulses in optical fibers. The higher-order NLS equation includes the terms caused by third-order dispersion, [ 22 ] self-steepening, [ 23 ] self-frequency shift effects, [ 24 ] and so on. However, it is more difficult to deal with both in physics and mathematics because the higher-order NLS equation is a higher-order nonlinear partial differential equation. Many authors have obtained dark and bright solitary wave solutions [ 25 – 29 ] and W-shaped solitary wave solutions [ 30 ] of a higher-order equation by using various methods, such as the Hirota algorithm, [ 31 ] traveling wave transformation, [ 32 ] and Darboux transformation. [ 33 – 35 ] Some types of exact N -soliton solutions [ 36 – 41 ] are reported for the higher-order nonlinear equation. In this paper, we will investigate Kuznetsov–Ma soliton and Akhmediev breather solutions of the higher-order NLS equation. In terms of Darboux transformation we obtain the analytical soliton solutions and breather solutions on a continuous wave (cw) background. The higher-order effects on the breather solution are discussed in detail.
The higher-order NLS equation [ 42 ] takes the form
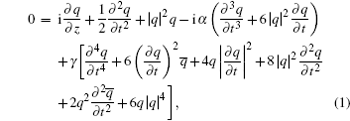
Modulation instability (MI) [ 48 ] as a parametric process exists by the interplay between dispersive and nonlinearity effects, in which a continuous or quasi-continuous wave experience a modulation of its amplitude or phase in the presence of weak perturbation. [ 49 ] Therefore, it may act as a precursor for the formation of bright solitons. Conversely, the stable dark solitons will exist if the absence of MI is under the constant intensity background. The phenomenon of MI has been discussed and studied in many physical systems. The MI process of the steady-state solutions can be discussed by introducing the following perturbed solution:
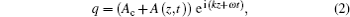
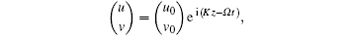
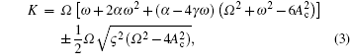
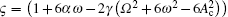
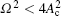
The higher-order NLS equation can be presented by the condition of compatibility of the Lax equation as

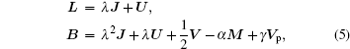


In the above equations the overbar stands for the complex conjugate. It is easy to verify that equation (

Following the standard procedure of Darboux transformation, [ 50 – 52 ] we obtain the soliton solution of Eq. (
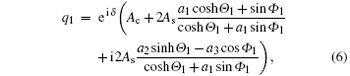

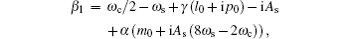
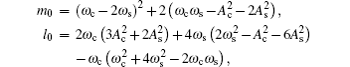
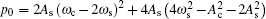
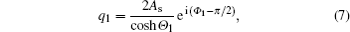
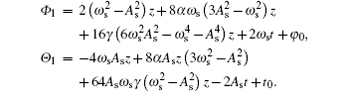
Therefore, equation (
When A c ≠ 0, ω c = −2 ω s , and 
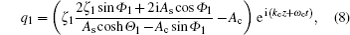
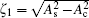

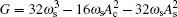
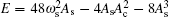
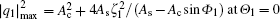
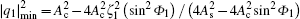
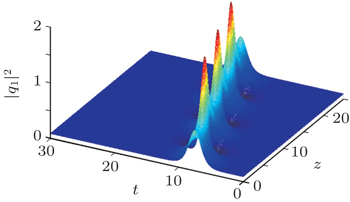 | Fig. 1. Evolution of Kuznetsov–Ma soliton solution in Eq. ( |
From Fig. 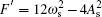


Figure 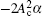
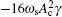
When A c ≠ 0, ω c = − 2 ω s , and 



In summary, we have exactly solved the higher-order integrable NLS equation which describes the propagation of ultrashort optical pulse in optical fibers. We have discussed the modulation instability process in detail and obtained the modulation instability conditions for a higher-order nonlinear equation. Based on the Lax pair and Darboux transformation method, bright solitary soliton solutions on a continuous wave background have been presented. With the different parameters, we give the Kuznetsov–Ma soliton and Akhmediev breather solutions of the higher-order nonlinear Schrödinger equation. The propagation characteristics of those solutions on a cw background have been analyzed in detail. When the amplitude of cw light exceeds the half of the soliton amplitude, this one-soliton solution describes the modulation instability process that can be used in practice to produce a train of ultrashort optical soliton pulses. However, the amplitude of cw light is less than half of the soliton amplitude, the one-soliton solution describes the propagation of a bright pulse on the cw background in the presence of higher-order effects, and the soliton’s peak position is shifted owing to the presence of a nonvanishing background field amplitude.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 |





