Cite this Article
Deng Min-Yi, Zhang Xue-Liang, Dai Jing-Yu. Effects of abnormal excitation on the dynamics of spiral waves. Chinese Physics B , 2016, 25(1): 010504  
Permissions
Effects of abnormal excitation on the dynamics of spiral waves
Deng Min-Yi †, , Zhang Xue-Liang , Dai Jing-Yu
College of Physical Science and Technology, Guangxi Normal University, Guilin 541004, China

 

† Corresponding author. E-mail: dengminyi@mailbox.gxnu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11365003 and 11165004).

Abstract
Abstract

The effect of physiological and pathological abnormal excitation of a myocyte on the spiral waves is investigated based on the cellular automaton model. When the excitability of the medium is high enough, the physiological abnormal excitation causes the spiral wave to meander irregularly and slowly. When the excitability of the medium is low enough, the physiological abnormal excitation leads to a new stable spiral wave. On the other hand, the pathological abnormal excitation destroys the spiral wave and results in the spatiotemporal chaos, which agrees with the clinical conclusion that the early after depolarization is the pro-arrhythmic mechanism of some anti-arrhythmic drugs. The mechanisms underlying these phenomena are analyzed.

PACS : 05.45.–a ; 87.18.Hf
Keyword : cellular automaton ; abnormal excitation ; transmembrane potential ; spiral wave
1. Introduction

Spiral waves exist widely in nature, such as the oxidation of CO on platinum, [ 1 ] the physical system, [ 2 ] and the neuronic system, [ 3 , 4 ] etc. Researchers studied the dynamics of spiral waves in different systems, [ 5 – 13 ] among which the spiral waves in myocardium is one of the hot topics. [ 11 – 13 ] The results showed that the spiral waves appearing in myocardium is one of the reasons for tachyarrhythmia, and the spatiotemporal chaos generated from spiral waves will lead to fibrillation, which is the main cause of sudden cardiac death. [ 14 ] Some factors affect the dynamics of spiral waves during tachyarrhythmia, such as the mechanical deformation, [ 11 ] electrophysiological heterogeneity, [ 12 ] and the early after depolarization (EAD). [ 13 ]

EAD is a secondary depolarization phenomenon that occurs occasionally before the completion of repolarization of an action potential. [ 15 ] The interest in EAD can be traced back to decades ago. In 1989, the clinical experimental results indicated that some anti-arrhythmic drugs had actually increased mortality, [ 16 ] and then EAD was considered to be one pro-arrhythmic mechanism of these drugs in 1992. [ 17 ] From then on, topics about EAD have been studied, such as the mechanisms underlying the EAD, [ 18 ] the predictors of the EAD-induced cardiomyopathy, [ 19 ] the relation between the EAD and the cardiac arrhythmias, [ 13 ] etc. The EAD includes the supernormal excitation and the abnormal excitation. [ 15 ] The effect of the supernormal excitation on the spiral waves has been discussed numerically, [ 20 ] but the numerical investigations about the abnormal excitation are lacking.

The abnormal excitations are considered as the result of the modification of the ion channel and/or electrogenic pump currents, and they can be induced in several experimental models. [ 17 ] In contrast to the supernormal excitation, the probability of the abnormal excitations is very low, because they appear occasionally. [ 15 ] When the abnormal excitation happens, a cell can be excited under a lower stimulation but cannot be excited as the stimulation is higher. [ 15 ] In this paper, the effect of abnormal excitation on spiral waves in the ventricle is studied using cellular automaton model.

The organization of the rest of the paper is as follows. First, the cellular automaton model for the ventricle considering the abnormal excitation is introduced. After that, the computer simulation results and the analysis are presented. The conclusion is provided finally.

2. Model

For simplicity, the differences of the repolarization characteristics between cells in different layers of the ventricle are ignored here, and then the transmembrane potential is divided into 14 states according to the electric characteristics of the ventricular cell. [ 21 ] The relation between the states and the transmembrane potential is shown in Fig. 1 .

Fig. 1. Relation between the states and the transmembrane potential of a ventricular cell. Symbols ○, •, and ⋆ represent the rest, excited, and refractory states, respectively.

The ventricle slice is put on the xoy coordinate surface and divided into 256 × 256 lattices, and the cells are distributed on these grid points. The no-flux boundary conditions and the Moore neighborhood are used throughout this paper. For the neighborhood radius R , there are (2 R + 1) 2 − 1 neighbors in a cell’s neighborhood. The state of the cell ( x , y ) at t is represented by u x , y ( t ) ∈ (0, 1, 2, …, 13), where u x , y ( t ) = 0, 1 denote the rest and excited state, respectively, while the states of u x , y ( t ) = 2, …,13 represent the refractory states. Under the normal conditions, the time evolution of a cell is given as follows:

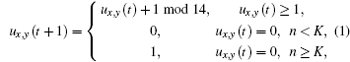
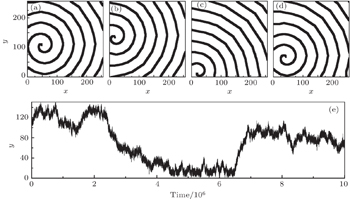
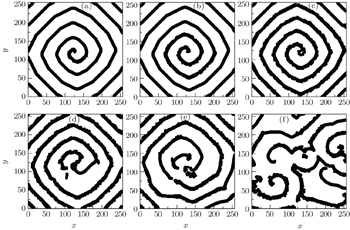
where n is the number of the excited cells in the neighborhood of the cell ( x , y ) at time t and K is the excitation threshold. For a fixed R , the excitability of the system decreases as K increases.

The electric impulse coming from the sinoatrial node can be impressed only when the excitability of the ventricular myocyte is high enough. In the above model, for R = 3, the spiral waves can be formed only when K ≤ 7: a plane wave produced initially ( t = 0) is cut at t = 40, and then the spiral wave comes into being (Fig. 2 ). The tip of the spiral wave is defined as an excited point which has both excited, refractory, and rest neighbors next to it.

Fig. 2. Spiral waves in a system without abnormal excitation under R = 3, R = 6 ((a) and (b)) and R = 3, K = 7 ((c) and (d)). Panels (a) and (b) illustrate the distribution of the excited state, where the black represents the excited state, the white represents the rest and refractory state. Panels (c) and (d) show the tip trajectories of the corresponding spiral waves.

Because the abnormal excitations occur before the completion of repolarization of an action potential, [ 15 ] the state 13 can be excited with abnormal excitation probability P for every cell in this model. After considering abnormal excitation, the time evolution of states [0, 12] is still in the form of Eq. ( 1 ), but the state 13 can be excited abnormally with a probability P according to

where P random is a random variable induced by computation at every step for every cell; K 1 and K 2 are the lower and upper limits of the abnormal excitable threshold, respectively. Obviously, according to Eq. ( 2 ), a cell can be excited under a lower stimulation but cannot be excited as the stimulation is higher when 0 < K 1 < K 2 < K . Meanwhile, P represents the abnormal excitation probability. Hence, the cellular automaton model with the introduction of the parameters K 1 , K 2 , and P can simulate the abnormal excitation. The different values of K 1 , K 2 , and P represent different abnormal excitations, for example, considering the properties of the abnormal excitation, the physiological abnormal excitation can be represented by P = 0.01 under appropriate K 1 and K 2 , while P = 0.26 means that the abnormal excitation is pathological. [ 15 ]

3. Simulation results
3.1. The effect of the physiological abnormal excitation on spiral waves

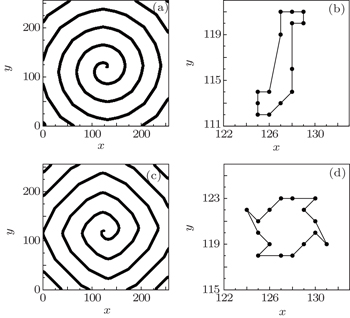
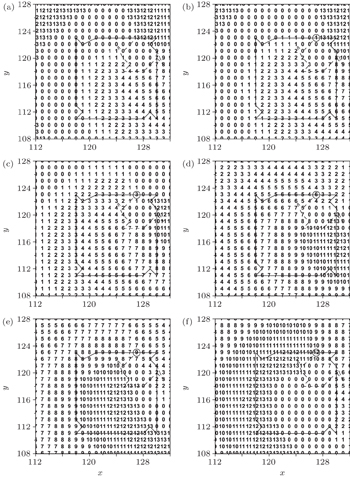
Because the plane wave can be formed and evolved only when K ≤ 7 for R = 3, so the lower and higher excitability of the medium may be represented by K = 7 and K = 6, respectively (the further results show that the conclusions obtained from K < 6 are the same as that from K = 6). The results have indicated that the excitability of the medium affects the dynamics of the spiral waves, [ 22 ] so the effect of the physiological abnormal excitation under different excitabilities will be discussed in the following. To investigate the effect of the physiological abnormal excitation on the spiral waves when the medium is highly excitable, the physiological abnormal excitation represented by K 1 = 3, K 2 = 5, and P = 0.01 is added in the system producing Fig. 2(a) after t = 201. The computer simulation results show that the form and wavelength of the spiral wave change hardly at all after the abnormal excitations occur (Figs. 3(a) – 3(d) ), although the spiral wave begins to meander irregularly with a very low velocity (Fig. 3(e) ). The constant of the form and wavelength means that the physiological abnormal excitation hardly affects the tachyarrhythmia when the ventricle is highly excitable. To analyze the mechanism underlying this phenomenon, the state distributions near the tip are offered in Fig. 4 .

Fig. 3. Distributions of the excited state at (a) t = 1000000, (b) t = 1800000, (c) t = 4500000, and (d) t = 10000000, where the black represents the excited state, and the white represents the rest and refractory state. Panel (e) shows the orbit of the spiral tip in the y direction. Here, R = 3, K = 6, K 1 = 3, K 2 = 5, P = 0.01.
Fig. 4. The state distributions at (a) t = 300 and (b) 301. The numbers represent the states, and the circle represents that the point has been excited abnormally. The parameters are the same as that in Fig. 3 .

Figure 4 indicates that (i) every rest cell can be excited normally at the next step, meanwhile, just the state 13 cells next to the rest cells can be excited abnormally owing to the low P and high K 1 . These two phenomena make sure that the states 1 coming from abnormal excitation are next to those coming from the normal excitation, and so the continuity of the distribution of state 1 cannot be broken, i.e., the form of the spiral wave remains nearly constant. (ii) At each time step, very few cells are excited abnormally owing to the low P , for example, in the region showing in Fig. 4 , just the cell (128, 113) is excited abnormally at t = 300 and it turns from state 13 to state 1 at t = 301. At the same time, the cells which have been excited abnormally distribute nearly symmetrically in the medium. These two phenomena make sure that the effects of the abnormal excitation on the wavelength of the spiral wave are offset, and then the wavelength hardly changes.

The excitability of the myocyte decreases with the cells aging. [ 23 ] To investigate the effect of the physiological abnormal excitation on the spiral waves in low excitable medium, the abnormal excitation represented by K 1 = 3, K 2 = 5, P = 0.01 is added in the system producing the Fig. 2(c) after t = 201 steps. The simulation results in a new stable spiral wave (Fig. 5 ).

Fig. 5. (a) Distribution of the excited state at t=100000, where the black represents the excited state, and the white represents the rest and refractory states. Panel (b) shows the tip trajectory. Here, R = 3, K = 7, K 1 = 3, K 2 = 5, P = 0.01.

Figure 5 indicates that the new spiral wave has a wider wavelength and a bigger tip trajectory. To uncover the mechanism underlying this phenomenon, the state distributions near the tip are followed (Fig. 6 ), and the tip trajectories before and after the abnormal excitation are also shown in Fig. 6 .

Fig. 6. The state distributions at (a) t=488, (b) 489, (c) 491, (d) 494, (e) 497, and (f) 500, where the numbers represent the states; the circle represents that the cell has been excited abnormally; the dashed and solid lines represent the tip trajectories before and after the abnormal excitation, respectively. The parameters are the same as those in Fig. 5 .

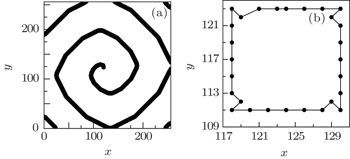
Comparing Fig. 6 with Fig. 4 , one can find that as the system is low excitable, there are much more rest cells in Fig. 6 than in Fig. 4 , and so the abnormal excitation can no longer happen far from the tip again. Figure 6(a) indicates that the tip goes along the original trajectory and there are no excited cells within the trajectory before the abnormal excitation happens. At t = 489, the cell (127,123) is excited abnormally (Fig. 6(b) ), and this cell is not next to the state 1 coming from the normal excitation. Because of the abnormal excitation, the excited state appears in the original tip trajectory (Fig. 6(c) ). After a few steps, the excited state meets the refractory state when it evolves along the original tip trajectory (Fig. 6(d) ), which excludes the tip moving along the original trajectory (Fig. 6(e) ) continually, and then the tip moves to a new trajectory (Fig. 6(f) ). Owing to the much wider new wavelength, the distance between the state 13 and the state 1 is larger than R even near the tip, so the abnormal excitation cannot occur again, i.e., the new stable spiral wave is stable.

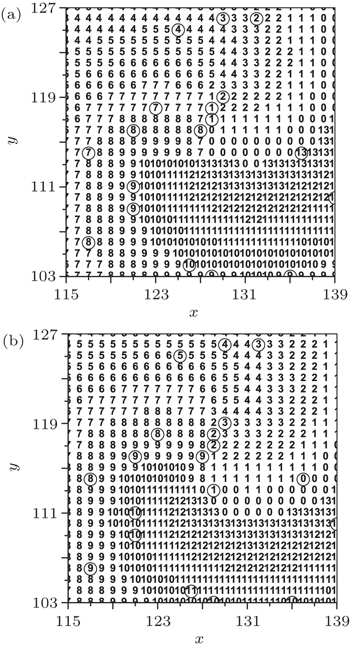
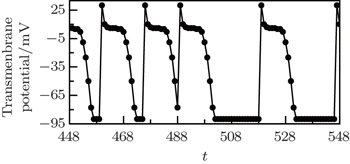
When the cell (127, 123), which is on the original tip trajectory, is selected randomly to be abnormally excited, it cannot return to 0 but to 1, so it undergoes the series of refractory states again, and the interval between its successive state 1 is twice of the states number, i.e., twice of 14. This means that the period of the new tip is 28. Because the tip is the controller of the spiral wave, [ 24 ] so the system falls into the new spiral wave with period of 28. To test the above analyses, the transmembrane potential of cell (127, 123) is followed, and the result is shown in Fig. 7 . Figure 7 indicates that the period of the transmembrane potential increases from 16 to 28. The further computer simulations result in the same change for every cell in this system, which means that the system evolves with a period of 28 really. The longer period of the new spiral wave means that the physiological abnormal excitation can mitigate the tachyarrhythmia when the system is low excitable.

Fig. 7. The trajectory of transmembrane potential of cell (127, 123). The parameters are the same as that in Fig. 5 .
3.2. The effect of the pathological abnormal excitation on spiral waves

Data from the clinical experimental studies suggest that the abnormal excitation happens more frequently in hypertrophied ventricles than in normal ventricles, i.e., the abnormal excitation turns from physiological to pathological in hypertrophied ventricles, which will lead to fatal fibrillation. [ 25 ] To investigate the effect of the pathological abnormal excitation on the spiral waves, the abnormal excitation represented by appropriate P , K 1 , and K 2 are added into the system producing the Fig. 2(c) after t = 201 steps. The computer simulation results show that the abnormal excitation cannot only result in a new spiral wave as Fig. 5(a ) qualitatively, but also break the spiral and bring in the spatiotemporal chaos (Fig. 8 ). One can see from Fig. 8 that the spiral waves can be destroyed and the spatiotemporal chaos appear under K 1 = 1 and P ≥ 0.26. According to the properties of the abnormal excitation, [ 15 ] both K 1 = 1 and P ≥ 0.26 mean that the abnormal excitation is pathological, so the results shown in Fig. 8 indicate that the pathological abnormal excitation can lead to the fibrillation. The clinical results have showed that some anti-arrhymic drugs can actually increase mortality, [ 16 ] and the early after depolarizations are considered to be one pro-arrhythmic mechanism of these drugs. [ 17 ] The results shown in Fig. 8 agree with these clinical conclusions. [ 16 , 17 ]

Fig. 8. The phase diagrams under (a) K 2 = 5 and (b) K 1 = 1, where the symbols s and c represent that the abnormal excitation results in a new spiral wave and the spatiotemporal chaos, respectively. The other parameters are R = 3 and K = 7.

As an example, figure 9 exhibits the process of the spiral breakup and the production of the spatiotemporal chaos under R = 3, K = 7, K 1 = 1, K 2 = 5, P = 0.26: because of the very small lower limit of the abnormal excitable threshold ( K 1 = 1) and the large abnormal excitation probability ( P = 0.26), the abnormal excitation happens not only near the tip first but also to the area far from the tip subsequently, and the wave fronts of these places get rough (Figs. 9(a) and 9(b) ); some cells in the state 1 coming from the abnormal excitation are not next to those coming from the normal excitation, so a new wave source appears near the tip (Fig. 9(c) ); and then more and more sources come into being (Figs. 9(d) and 9(e) ), which results in the spatiotemporal chaos finally (Fig. 9(f) ).

Fig. 9. Distributions of the excited state at (a) t = 216, (b) t = 233, (c) t = 265, (d) t = 298, (e) t = 343, and (f) t = 10100 under R = 3, K = 7, K 1 = 1, K 2 = 5, and P = 0.26, where the black represents the excited state, and the white represents the rest and refractory states.
4. Conclusion

The abnormal excitation is a modality of early after depolarization, and it appears occasionally in myocytes. Under the normal conditions, the electric impulse moves throughout the heart with plane waves or target waves, which make sufficient distance between the last refractory state and the excited state, so the abnormal excitation cannot happen for these wave patterns. But for the spiral pattern, the abnormal excitation can occur and play a role. In this paper, the effect of physiological and pathological abnormal excitation on the spiral waves is studied based on the cellular automaton model of a ventricle slice. The computer simulation results can be summarized as follows. (i) For the medium with a high excitability, the physiological abnormal excitation causes the stable spiral wave to meander irregularly with a very low velocity, but the form and the wavelength of the spiral wave hardly change. This phenomenon means that the physiological abnormal excitation hardly affects the tachyarrhythmia when the ventricle is highly excitable. (ii) For the medium with a low excitability, the physiological abnormal excitation happening on the tip trajectory blocks the movement of the excited state along the original trajectory, so the tip leaves the original trajectory and falls into a new trajectory finally, i.e., the system turns into a new spiral wave pattern. The period of this new spiral wave is longer than the original, which means that when the system is of low excitability, the physiological abnormal excitation can mitigate the tachyarrhythmia. (iii) For the system with a low excitability, the pathological abnormal excitation may cause the break up of the spiral waves and result in the spatiotemporal chaos, which agrees with the clinical conclusions that the early after depolarizations is the pro-arrhythmic mechanism of some anti-arrhythmic drugs. This paper uncovers the mechanisms of the effect of the abnormal excitation on spiral waves on cellular level, and the results give an insight into the mechanisms of some anti-arrhythmic drugs.

Reference
1 Jakubith S Rotermund H H Engel W Oertzen A V Ertl G 1990 Phys. Rev. Lett. 65 3013
2 Larionova Y Egorov O Cabrera-Granado E Esteban-Martin A 2005 Phys. Rev. A 72 033825
3 Ma J Zhang A H Tang J Jin W Y 2010 J. Biol. Syst. 18 243
4 Zhang L S Gu W F Hu G Mi Y Y 2014 Chin. Phys. B 23 108902
5 Petrov V Ouyang Q Swinney H L 1997 Nature 388 655
6 Nejad T M Lannaccone S Rutherford W lannaccone P M Foster C D 2015 Biomech. Model. Mechanobiol. 14 107
7 Liu G Q Wu N J Ying H P 2013 Commun. Nonlinear Sci. 18 2398
8 Zhao Y H Lou Q Chen J X Sun W G Ma J Ying H P 2013 Chaos 23 033141
9 Zhang H Chen J X Li Y Q Xu J R 2006 J. Chem. Phys. 125 204503
10 Li W H Li W X Pan F Tang G N 2014 Acta Phys. Sin. 63 208201 (in Chinese)
11 Keldermann R H Nash M P Gelderblom H Wang V Y Panfilov A V 2010 Am. J. Physiol. Heart Circ. Physiol. 299 H134
12 Xie F G Qu Z L Garfinkel A Weiss J N 2001 Am. J. Physiol. Heart Circ. Physiol. 280 H535
13 Weiss J N Garfinkel A Karagueuzian H S Chen P S Qu Z L 2010 Heart Rhythm 7 1891
14 Nasha M P Panfilov A V 2004 Prog. Biophys. Mol. Biol. 85 501
15 Yan Q Guan D L Yang H Yan H W 2012 A Concise Handbook of Electrocardiogram Beijing People’s Medical Publishing House (in Chinese)
16 Gottlieb S S 1989 Am. Heart J. 118 1074
17 January C T Moscucci A 1992 Ann. NY Acad. Sci. 644 23
18 Ye P Grosu R Smolka S A Entcheva E 2008 Lect. Notes Comput. Sci. 5307 141
19 Pol L C Deyell M W Frankel D S Benhayon D Squara F Chik W Kohari M Deo R Marchlinski F E 2014 Heart Rhythm 11 299
20 Wei H M Tang G N 2011 Acta Phys. Sin. 60 030501 in Chinese
21 Antzelevitch C 2001 Cardiovasc. Res. 50 426
22 Chen J X Mao J W Hu B B Xu J R He Y F Li Y Yuan X P 2009 Phys. Rev. E 79 066209
23 Stein M van Veen T A B Hauer R N W de Bakker J M T van Rijen H V M 2011 PLoS ONE 6 1
24 Otani N F 2002 Chaos 12 829
25 Levy D Garrison R J Savage D D Kannel W B Castelli W P 1990 New Engl. J. Med. 322 1561