The study of the magnetic properties of the mixed Cu(110) deposited bimetallic Au– Co nanowires was carried out using the Vienna ab-initio simulation package (VASP)^[20] based on the density functional theory (DFT).^[21] The cutoff energy 250  eV was used. We have also tested the effect of cut-off energy 250– 300  eV on the total energy of the system. Our study revealed no significant differences in the calculation of the total energy of the system (< 1  meV). The generalized gradient approximation (GGA) for the exchange– correlation functional was applied using the Perdew– Wang treatment.^{[22– 24]} The structural relaxation was performed via a quasi-Newton algorithm, using the exact Hellmann– Feynman forces acting on each atom.^[25] The total energies of the system were converged up to 1  meV/atom, while the residual force acting on each atom was less than 0.01  eV/Å . For the atomic relaxation of the system, the second-order Methfessel– Paxton method^[26] was used. The integration over the Brillouin zone (BZ) was performed using the tetrahedron method with Blö chl corrections. BZ sampling was performed using 3 × 3 × 1 k-point mesh in the Mankhorst– Pack grid.^[27] Our calculations of the total energy with different k-point meshes (2 × 2 × 1, 3 × 3 × 1, 4 × 4 × 1, 5 × 5 × 1) have shown that the 3 × 3 × 1 k-point mesh is sufficient to study the electronic and structural properties of the Au– Co nanowires on a Cu(110) surface. The structure of the Cu(110) deposited Au– Co nanowires was represented by a three-dimensional supercell with periodic boundary conditions. The mixed Au– Co nanowire was modeled as a four-atom chain of two Au atoms and two Co atoms (see Fig.  1(a)). The sizes of the supercell along x and y directions were chosen to be sufficiently large (∼ 10  Å ) in order to avoid the interaction between the wire and its image. The surface was represent as a slab of five atomic Cu layers with thickness ∼ 8  Å along the z direction and separated from one another by a vacuum layer which was large enough to exclude any interaction between the slabs.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) The atomic structure of the Au– Co nanowire deposited on Cu(110) surface used for the present slab supercell modeling. (b) The relaxed interatomic distances.

For the simulation of magnetization dynamics, we applied the kMC method proposed by Li and Liu.^[28] We assumed that only Co atoms have nonzero magnetic moments. Thus in the absence of external magnetic fields, the Hamiltonian of the model can be written in the Heisenberg form

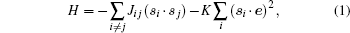
where s_i and e point the directions of the magnetic moments of the Co atoms and the easy magnetization axis, J_ij are the exchange energies, and K is the energy of magnetic anisotropy. We assumed that only the nearest neighboring Co atoms can interact, J_ij = J(δ _{i, j+ 1} + δ _{i, j– 1}), where δ _ij is the Kronecker delta. Directions s_i of the magnetic moments have two metastable states: the first is parallel to e and the second is antiparallel to e.

The rotation of the i-th magnetic moment can occur in two different ways. If 2K > | h_i| , where h_i = ∑ _jJ_ij(s_i · s_j), then the rotation of the magnetic moment has a barrier

The frequency rate of such rotations is calculated by means of the Arrhenius law

where k_B is the Boltzmann constant, T is the copper substrate’ s temperature, and ν ₀ = 10⁹  Hz^[29] is the frequency prefactor. If 2K ≤ | h_i| , then there is no barrier, and Glauber dynamics^[30] can be applied to compute the frequency rate

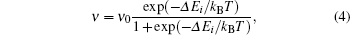
where Δ E_i is the difference between the energies of the system before and after the rotation. Transition rates (3) and (4) were also used to calculate the real-time increment of each kMC step.^[31]

Our previous works^{[7, 32]} showed that the dimerization of Co atoms in the freestanding nanowire leads to destabilization of the nanowire and to the vanishing of the magnetic anisotropy in the system. Thus, only evenly mixed Au– Co wires were studied in the present article. At the first, the atomic relaxation of the wire was carried out. We observed the displacement of atoms in the vertical direction: cobalt atoms move towards the Cu surface, gold atoms move out from the Cu surface. As a result, the Au– Co nanowire takes a zig-zag configuration with relative displacements of atoms from the wire axis about 0.18  Å . The relaxed interatomic distance between Au and Co atoms in the wire is about 2.52  Å . The relaxed interatomic distances between Co and Cu and between Au and Cu atoms are shown in Fig.  1(b).

The calculations of the magnetic properties show that the local magnetic moment of the Co atom in the deposited Au– Co nanowire is about 2.0μ _B. Due to the interaction of the Co atoms with the Cu surface, the local magnetic moment is less than the magnetic moment of the Co atom (2.35μ _B) in the freestanding Au– Co nanowire at the corresponding interatomic distance 2.5  Å .

Our first-principle calculations show the emergence of GMA in the mixed Au– Co nanowires, by which we mean finite magnetization exists along certain directions, but vanish along other directions (e.g., orthogonal). The magnetic anisotropy is caused by the large orbital magnetization and the strong spin– orbit coupling.^[33] We carried out a series of calculations with different possible directions of the magnetization axis: along the nanowire axis (axial magnetization) and orthogonal to it (vertical magnetization and in-plain orthogonal magnetization). The results of our calculation are presented in Tables  1 and 2.

The easy magnetization axis corresponds to the X wire direction, i.e., the in-plain axial magnetization of the Cu(110) surface. The vertical Z direction of the magnetic moments represents the hard magnetization axis; the MAE is (E_Z – E_X)/2 = 7  meV per Co atom. The minimal value of MAE corresponds to the in-plain rotation of the magnetic moment from the orthogonal to the wire direction to the axial direction, (E_Y – E_X)/2 = 3  meV per Co atom. The MAE for the rotation of the magnetic moment around the wire axis is (E_Z – E_Y)/2 = 4  meV per Co atom.

The connection between the orbital moments and the MAE in supported nanostructures and adatoms was discussed in detail in a previous work.^[33] Our calculations show that the spin magnetic moment of the Co atoms in the Au– Co supported nanowires, μ _S, is about 1.8μ _B and it is the same for all directions of the magnetization axis. At the same time, the orbital magnetic moment μ _L depends on the direction of the magnetization axis. The orbital magnetic moment is 0.35μ _B in the case of axial magnetization, and 0.22μ _B for orthogonal in-plain magnetization.

Table 1.

Table 1.

Table 1. Calculated spin magnetic moments μ S, orbital magnetic moments per Co atom in the Au– Co nanowire μ L, and total energies of the Au– Co nanowire on the Cu(110) surface E. Direction of magnetization axis μ S/μ B μ L/μ B E/eV In-plane axial (X) 1.75 0.35 − 132.697 In-plain orthogonal (Y) 1.76 0.22 − 132.691 Out-plain vertical (Z) 1.75 0.16 − 132.683

Table 1. Calculated spin magnetic moments μ S, orbital magnetic moments per Co atom in the Au– Co nanowire μ L, and total energies of the Au– Co nanowire on the Cu(110) surface E.

Table 2.

Table 2.

Table 2. The magnetic anisotropy energy per two Co atoms of the Au– Co nanowire on the Cu(110) surface with X, Y, and Z (see Fig.  1(a)) directions of the magnetization axis, and difference of the total energies of ferromagnetic and antiferromagnetic states of the Au– Co nanowire on the Cu(110) surface for X direction (EFM – EAFM). All calculated values are converged to within 0.01  meV per magnetic atom with respect to k-points used. EY – EX EZ – EY EZ – EX EFM – EAFM 6  meV 8  meV 14  meV – 41  meV

Table 2. The magnetic anisotropy energy per two Co atoms of the Au– Co nanowire on the Cu(110) surface with X, Y, and Z (see Fig.  1(a)) directions of the magnetization axis, and difference of the total energies of ferromagnetic and antiferromagnetic states of the Au– Co nanowire on the Cu(110) surface for X direction (EFM – EAFM). All calculated values are converged to within 0.01  meV per magnetic atom with respect to k-points used.

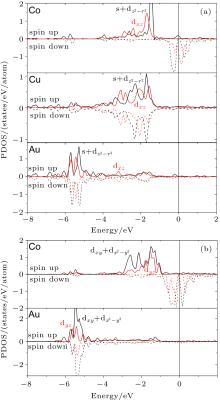
To explain the emergence of GMA and its dependence on the geometry of the wire, we studied the electronic structure of the supported Au– Co nanowire. The band structure of the Au– Co nanowire is presented in Fig.  2. Our band structure calculations show that the s and d states of each atom form new hybrid bands: an d_xy + d_{x²– y²} band lying in the plane of the Cu(110) surface, d_xz and d_yz bands lying out of the Cu(110) plain, an s + d_{z²– r²} band located along the vertical axis (z), and s + d_{z²– r²} and d_xz bands involved in bonding of the nanowire and the surface atoms (Fig.  2(a)). These bands possess strong spin-splitting about 1.5– 2.0  eV on the Fermi level. As a result, the main contribution to the magnetization of the wire is given by the s + dz²– r² and d_xz bands. We found the strong hybridization between the d_xy + d_{x²– y²} and d_yz bands of the Au and Co atoms (Fig.  2(b)). The formation of atomic bonds into the wire between the Au and Co atoms occurs by means of the d_xy + d_{x²– y²} and d_yz bands. The d_xy + d_{x²– y²} states were identified as the main source of the magnetic anisotropy.^[34] The spin-splitting of these bands on the Fermi level is about 1.0  eV. Thus its contribution to the magnetization of the Au– Co nanowire is less than that of the s + d_{z²– r²} and d_xz bands, as a result, the MAE in the present system decreases significantly in comparison to that of the freestanding nanowire. In turn, the ferromagnetic order in the mixed wire is caused by strong band hybridization of the d and s states of the Au, Co, and Cu surface atoms. The direct exchange interaction is sustained by the hybridization of the d_xy + d_{x²– y²} and d_yz bands of the Au and Co atoms and also by the s + d_{z²– r²} and d_xz bands hybridization of the Co and Cu atoms (Fig.  2). The band structure of the freestanding Au– Co nanowires was investigated in a previous work.^[17]

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The partial density of states (PDOS) of bimetallic Au– Co nanowires deposited on the Cu(110) surface: (a) s + dz2– r2 and dxz states for Co, Au atoms of the nanowire and nearest Cu atoms of the surface copper layer effective interacting with the Au– Co nanowire, (b) dxy + dx2– y2 and dyz states of Au and Co atoms of the nanowire. The Fermi level lies at E = 0.

We treated the long finite Au– Co chains as infinite Au– Co nanowires to investigate the magnetic properties. According to the DFT results presented in Table  2, we took the facts that the easy magnetization axis of the Co atoms in the Au– Co chain is orientated along the chain direction, only the in-plain rotations of the magnetic moments may occur at low temperatures, the anisotropy energy per Co atom K = (E_Y – E_X)/2 = 3  meV, and the exchange energy J = – (E_FM – E_AFM)/8 = 5.125  meV. The magnetization is normalized to 1 when all the magnetic moments are orientated along the X direction. We used the free boundary conditions and started with an initial state with a random distribution of the magnetic moments ((s_i · e) = 1 or (s_i · e) = – 1). To find the temperature dependence of the time-average absolute magnetization | M| (T), the system was first relaxed into thermodynamical equilibrium using 10⁶  kMC steps for each temperature. Then, we calculated the absolute magnetization averaged over 1 min for each temperature step.

It is well known^[35] that the spontaneous magnetization (M) of macroscopic ferromagnets near the Curie point decreases as M ∼ (T_C – T)^1/2, where T_C is the Curie temperature. Thus the magnetization M tends to zero and – dM/dT tends to infinity when the temperature T tends to T_C. So, if we have measured or calculated the temperature dependence M(T), we can easily find the Curie temperature. In the case of nanoscopic systems, the fluctuations of the spontaneous magnetization are too large. In this case, we can characterize the magnetic state of the nanostructures by the time-average absolute magnetization | M| . Unfortunately, | M| is always larger than zero. However, – d| M| /dT still has a sharp peak (see, for example, Fig.  3). The Curie temperature can be defined as the temperature of the maximum of – d| M| /dT. Figure  3 shows the time-average magnetization of the Au– Co chain consisting of 100  atoms of cobalt in the temperature range of 5– 65  K. To find the Curie temperature, we calculated central difference derivation – d| M| /dT, approximated the peak with a quadratic function, and found the maximum of this function. As a result, the Curie temperature of the Au– Co chain is found to be 25.2± 2.5  K. This value has the same order of magnitude as the critical temperature of the monoatomic Co chains on Pt surfaces.^{[28, 29]}

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The time-average magnetization | M| (white circles) and the central difference derivation – d| M| /dT (black circles) as a function of temperature T. The Au– Co chain consists of 100 atoms of cobalt. The parameters of the Heisenberg Hamiltonian are J = 5.125  meV and K = 3  meV.

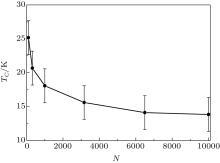
It is interesting to study how the Curie temperature T_C depends on the length of the chain. We calculated the Curie temperature of the Au– Co chains consisting of 100, 316, 1000, 3162, 6500, and 10000  atoms of cobalt. The results in Fig.  4 demonstrate a size effect: the Curie temperature decreases with elongation of the chain and tends to ∼ 13  K. This result is in agreement with the Mermin– Wagner theorem.^[36] From the theorem, it follows that if MAE tends to zero and the length of the chain tends to infinity, then the Curie temperature would tend to zero. In our case, the Curie temperature should tend to the finite limit for the infinitely long chain, because the Co atoms have nonzero MAE.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The Curie temperature of the Au– Co chain as a function of its length, where N is the number of Co atoms in the chain. The parameters of the Heisenberg Hamiltonian are J = 5.125  meV and K = 3  meV.

We studied the influence of the nonmagnetic copper substrate Cu(110) on the magnetic properties of bimetallic Au– Co nanowires. We found the emergence of magnetic anisotropy in the supported Au– Co nanowires. Our study revealed a strong increase of the exchange interaction energy in the Au– Co wire (∼ 41  meV per two Co atoms). The electronic structure calculation revealed the emergence of new hybridized bands between Au and Co atoms and surface copper atoms, which caused the strong decrease of the magnetic anisotropy and the increase of the exchange interaction energy. Using the results of the presented DFT calculation, we found a size effect: the Curie temperature decreases from 25.2± 2.5  K to 13.8± 2.5  K with elongation of the chain from 100  Co atoms to 10000  Co atoms. We believe that the presented investigation will be helpful for future technical applications.