†Corresponding author. E-mail: wlzuo@iphy.ac.cn
‡Corresponding author. E-mail: shenbg@aphy.iphy.ac.cn
*Project supported by the Beijing Natural Science Foundation, China (Grant No. 2152034) and the National Natural Science Foundation of China (Grant Nos. 11274357 and 51271196).
A series of CeMn2(Si1− xGe x)2 ( x = 0.2, 0.4, 0.6, 0.8) compounds are prepared by the arc-melting method. All the samples primarily crystallize in the ThCr2Si2-type structure. The temperature dependences of zero-field-cooled (ZFC) and FC magnetization measurements show a transition from antiferromagnetic (AFM) state to ferromagnetic (FM) state at room temperature with the increase of the Ge concentration. For x = 0.4, the sample exhibits two kinds of phase transitions with increasing temperature: from AFM to FM and from FM to paramagnetic (PM) at around TN ∼ 197 K and TC ∼ 300 K, respectively. The corresponding Arrott curves indicate that the AFM–FM transition is of first-order character and the FM–PM transition is of second-order character. Meanwhile, the coexistence of positive and negative magnetic entropy changes can be observed, which are corresponding to the AFM–FM and FM–PM transitions, respectively.
Investigation of the magnetocaloric effect (MCE) has attracted a great deal of attention owing to the potential application in magnetic refrigerators.[1– 9] The MCE is characterized by the isothermal magnetic entropy change or the adiabatic temperature change of a material when exposed to a varying magnetic field. The effect is an intrinsic property of the magnetic material and originates from the change in the coupling between the magnetic sublattice and the applied magnetic field. Therefore, the entropy change Δ SM is mainly governed by the magnitude of ∂ M/∂ T, and search for large MCE materials is normally associated with the first-order phase transitions, as a large difference in magnetization exists between two adjacent magnetic states.[3– 5]
During the last few years, many rare earth transition metal intermetallic compounds have been shown to possess giant MCE.[10– 12] Among the intermetallic compounds, the RMn2X2 (R = rare earth, X = Si or Ge) compounds crystallize in the tetragonal ThCr2Si2-type structure. The magnetic states as well as the types and orders of magnetic transition are highly sensitive to the interlayer Mn– Mn distance dMn− Mn. When dMn− Mn is larger than 2.87 Å (a > 4.06 Å , the interlayer coupling is ferromagnetic (FM), while the antiferromagnetic (AFM) phase is stable when dMn− Mn is smaller than 2.87 Å (a < 4.06 Å ).[13– 15] Therefore, the ternary RMn2X2 compounds, which show very interesting magnetism and MCE behaviors, [5, 12, 16] are good candidates to study the physical mechanism behind the MCE.
In this paper, the MCE of the CeMn2(Si1− xGex)2 (x = 0.2, 0.4, 0.6, 0.8) compounds are investigated. It is worth mentioning that in this family of compounds, the Ce atoms are nonmagnetic and the magnetism comes from the Mn atoms.[17, 18] Therefore, simple substitution of Si by Ge (Si and Ge have different atomic radii) will modify the interlayer Mn– Mn distance and make the magnetic state undergo series transition, which is important and useful to study the mechanism of the MCE.
The CeMn2(Si1− xGex)2 (x = 0.2, 0.4, 0.6, 0.8) compounds were prepared from Ce (99.9%), Mn (99.99%), Si (99.99%), and Ge (99.99%) by arc-melting in a high purity argon atmosphere. The mass loss of Mn during the melting was compensated by adding 2% excess Mn over the stoichiometric amount. The ingots were remelted three times to ensure homogeneity and then annealed at 1173 K for a week in vacuum. The phase structure and the crystal lattice parameters were examined at room temperature by the x-ray powder diffraction with Cu K α radiation. Magnetizations were measured as functions of temperature and magnetic field by employing a commercial superconducting quantum interference device (SQUID) magnetometer, model MPMS-7 from Quantum Design Inc. The temperature dependences of the magnetizations in both zero field-cooled (ZFC) and field-cooled (FC) processes were measured. In the ZFC measurement, the initial field was set to zero when cooling the sample from 300 K to 2 K, the magnetization was measured with a magnetic field of 0.01 T while heating the sample from 2 K to 300 K. In the FC measurement, the same magnetic field of 0.01 T was applied when cooling the sample from 300 K to 2 K.
Figure 1(a) shows the x-ray diffraction (XRD) patterns of the CeMn2(Si1− xGex)2 (x = 0.2, 0.4, 0.6, 0.8) compounds at room temperature. It is found that all the samples primarily crystallize in the ThCr2Si2-type structure with minor CeSiy (1.75 ≤ y ≤ 2) impurities. The Rietveld refinements are carried out for determination of the lattice parameters. The results are shown in Fig. 1(b). As expected, all the lattice parameters are increased with the increase of the Ge concentration. The interlayer Mn– Mn distance dMn− Mn is smaller than 2.87 Å when x ≤ 0.2, whereas dMn− Mn is larger than 2.87 Å when x ≥ 0.4. This change of dMn− Mn indicates that the magnetic states of the Mn2(Si1− xGex)2 compounds will change from AFM to FM, which will be demonstrated in the next section. In addition, the lattice parameter a shows a nonlinear increase, which is due to the Ce-valence instability with the Ge substitution.[19]
Figure 2 shows the temperature dependences of ZFC and FC magnetizations with a magnetic field of 0.01 T for the CeMn2(Si1− xGex)2 (x = 0.2, 0.4, 0.6, 0.8) compounds. For x = 0.2, the sample shows a sharp peak at around TN ∼ 334 K, indicating an AFM order. For x = 0.4, the sample first shows a transition from paramagnetic (PM) to FM at around TC ∼ 300 K, and then exhibits an AFM order at around TN ∼ 197 K. For x = 0.6 and 0.8, a normal PM– FM transition occurs at around TC ∼ 314 K and 317 K, respectively. In addition, a phase transition is observed at TC/C ∼ 36 K for x = 0.6, which is owing to the change of the canted ferromagnetic spin structure of the Mn moments into conical magnetic arrangements.[20] It is worth noticing a splitting between the ZFC and the FC measurement curves below TC for x = 0.4, 0.6, and 0.8. A similar phenomenon has also been observed by other researchers.[20– 22] In the ZFC case, the spins have a random domain configuration below TC, whereas in the FC case, the spins have a preferred orientation along the external field direction. Therefore, the magnetization is smaller in the ZFC case than that in the FC case. Furthermore, it can be seen that all the samples show a weak jump at around 10 K, which may be due to the small amount of impurities CeSiy (1.75 ≤ y ≤ 2).[19]
Figure 3 shows the magnetization isotherms and the corresponding Arrott curves of the CeMn2(Si0.6Ge0.4)2 compound with different temperature steps. For the regions of 182– 190 K and 296– 304 K, the step is 2 K, whereas the step is 3 K for the other unmarked temperature regions. From Fig. 3(a), we can find that the magnetization slowly increases with the increase of the magnetic field in a low field range owing to the existence of the AFM ground state below TN ∼ 197 K. However, with further increase of the field, the magnetization exhibits a sharp increase at the critical field Bc (Bc is defined as the field corresponding to the maximum of the ∂ M/∂ H– H curve). In addition, the critical field Bc gradually decreases with the increase of the temperature, which indicates that the field-induced AFM– FM transition can be achieved by a smaller field when the temperature increases; in other words, the AFM coupling becomes weaker with the increase of the temperature. Above TN ∼ 197 K, the typical FM magnetization nature can be found and no trace of metamagnetic behavior is observed from the M– H curves (see Figs. 3(a) and 3(c)). When the temperature further increases and exceeds TC ∼ 300 K, the PM magnetization behavior (a linear relation in the isothermal M– H curves) comes into being, as shown in Fig. 3(c). Meanwhile, figures 3(b) and 3(d) show the corresponding Arrott curves. According to the Banerjee criterion, [23] a magnetic transition is of first-order when the slope of the Arrott curves is negative, whereas it will be of second-order when the slope is positive. The S-shaped (negative slope) Arrott curves indicate that the field-induced AFM– FM transition is of first-order between 160 K and 202 K. On the contrary, the positive slope also demonstrates that the FM– PM transition is of second-order between 285 K and 325 K.
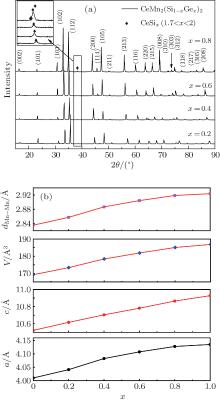 | Fig. 1. (a) The XRD patterns of CeMn2(Si1− xGex)2 (x = 0.2, 0.4, 0.6, 0.8) compounds at room temperature. (b) The dependence of the lattice parameters on the Ge concentration. |
 | Fig. 2. The temperature dependences of ZFC and FC magnetizations for CeMn2(Si1− xGex)2 compounds with a magnetic field of 0.01 T: (a) x = 0.2, (b) x = 0.4, (c) x = 0.6, (d) x = 0.8. |
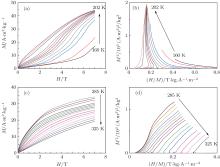 | Fig. 3. (a), (c) The magnetic isotherms and (b), (d) the corresponding Arrott curves of the CeMn2(Si0.6Ge0.4)2 compound. |
The entropy change Δ SM of the CeMn2(Si0.6Ge0.4)2 compound is calculated from the magnetization versus magnetic field data using the integrated Maxwell relation

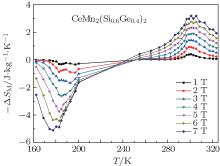
As shown in Fig. 4, the positive and negative peaks can be observed in the curves which are corresponding to the AFM– FM and FM– PM transitions, respectively. For the AFM– FM transition at around TN ∼ 197 K, the maximum values of Δ SM are around 1.0 J/kg· K, 3.8 J/kg· K, and 4.9 J/kg· K for the field changes of 2 T, 5 T, and 7 T, respectively. Furthermore, the Δ SM peak broadens asymmetrically toward low temperature with the increase of the magnetic field, which is normally the character of the first-order phase transition. Nevertheless, for the FM– PM transition at around TC ∼ 300 K, the maximum values of Δ SM are around − 0.9 J/kg · K, − 2.3 J/kg · K, and − 3.2 J/kg· K for the field changes of 2 T, 5 T, and 7 T, respectively. The increase of | Δ SM| is proportional to the increasing field, which together with the symmetrical broadening of the Δ SM peak are both the character of the second-order phase transition. It is interesting that the maximum values of | Δ SM| of the first-order AFM– FM metamagnetic transition are larger than those of the second-order FM– PM transition under the same field changes.
In this paper, the structure and magnetic properties of the CeMn2(Si1− xGex)2 (x = 0.2, 0.4, 0.6, 0.8) compounds are studied. The substitution of Si by Ge modifies the interlayer Mn– Mn distance and the magnetic states undergo a variety of phase transitions. The CeMn2(Si0.6Ge0.4)2 compound shows two kinds of phase transitions with temperature increasing from 160 K to 328 K. The Arrott curves indicate that the AFM– FM metamagnetic transition is of first-order character and the FM– PM transition is of second-order character. The corresponding maximum values of Δ | SM| of AFM– FM transition are larger than those of FM– PM transition under the same field changes.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|