Cite this Article
Wang Chang-Ying, Han Han, Shao Kuan, Cheng Cheng†, Huai Ping‡. Defect stability in thorium monocarbide: An ab initio study . Chinese Physics B, 24(9): 097101  
Permissions
Defect stability in thorium monocarbide: An ab initio study
Wang Chang-Yinga),b), Han Hana),c), Shao Kuana),b), Cheng Cheng†a),c), Huai Ping‡a),c)
Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China
University of Chinese Academy of Sciences, Chinese Academy of Sciences, Beijing 100049, China
Key Laboratory of Nuclear Radiation and Nuclear Energy Technology, Chinese Academy of Sciences, Shanghai 201800, China

†Corresponding author. E-mail: chengcheng@sinap.ac.cn

‡Corresponding author. E-mail: huaiping@sinap.ac.cn

*Project supported by the International S&T Cooperation Program of China (Grant No. 2014DFG60230), the National Natural Science Foundation of China (Grant No. 91326105), the National Basic Research Program of China (Grant No. 2010CB934504), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA02040104).

Abstract

The elastic properties and point defects of thorium monocarbide (ThC) have been studied by means of density functional theory based on the projector-augmented-wave method. The calculated electronic and elastic properties of ThC are in good agreement with experimental data and previous theoretical results. Five types of point defects have been considered in our study, including the vacancy defect, interstitial defect, antisite defect, schottky defect, and composition-conserving defect. Among these defects, the carbon vacancy defect has the lowest formation energy of 0.29 eV. The second most stable defect (0.49 eV) is one of composition-conserving defects in which one carbon is removed to another carbon site forming a C2 dimer. In addition, we also discuss several kinds of carbon interstitial defects, and predict that the carbon trimer configuration may be a transition state for a carbon dimer diffusion in ThC.

PACS: 71.15.Mb; 71.20.−b; 61.72.J−; 61.72.jj
Keyword: thorium monocarbide; ab initio study; bulk properties; defects
1. Introduction

Actinide carbides are considered to be one of the most promising nuclear fuel materials of generation-IV reactors. They have several advantages relative to standard actinide oxide fuels, [1– 3] such as a higher density, a higher thermal conductivity, and a better compatibility with clad materials.[4, 5] The relevant studies were concerned with both technological developments and fundamental scientific aspects. Previously, researchers have widely studied uranium carbide[6– 12] and mixed uranium-plutonium carbide.[13, 14] From the 1960s to 1970s, as a supplement for fertile fuel, thorium-based nuclear power was recognized and built as an experimental reactor by the Oak Ridge National Laboratory. Afterwards, thorium carbide and uranium carbide fuel were designed and developed in the peach bottom reactor project.[15] After several decades' intermission, the relevant experimental and theoretical studies for thorium carbide are attracting a great deal of attention.

Experimentally, thorium monocarbide (ThC) has a large domain of nonstoichiometry (ThCx with 0.55 < x < 1 at high temperature). [16] There are several relevant experimental works on thorium carbide which were mainly reported in the 1960s and 1980s.[17– 21] Through the investigation of the non-stoichiometry of ThC by Satow, [18] it can be deduced that the lattice defects of this compound are carbon vacancies. Gerward et al. did not observe structural phase transformation of ThC over the whole pressure range through the high-pressure x-ray diffraction studies.[16]

Theoretically, a few first-principle studies have been performed to understand the structural, electronic, elastic, and thermodynamic properties of ThC.[22– 29] Shein et al. calculated the electronic, structural, and mechanical properties of ThC from the first-principles study.[22– 25] Das et al. studied the electronic structure and elastic properties of transition metal series (Sc, Ti, V, Zr, and Hf) and actinides (Th, U) carbide based on the tight-binding linear muffin-tin orbitals method, and they found that the f states have features rather different from transition metal carbides.[26] Lim et al. studied the electronic properties of ThC by using Gaussiantype orbitals and density functional theory, and they found that Heyd– Scuseria– Ernzerhof (HSE) hybrid functional does not open a band gap near the Fermi energy in ThC.[27] Aydin et al. studied the pressure dependency of the structural, elastic and mechanical properties by using a first-principle method based on the LDA+ U functional.[28] Pé rez et al. reported the phonon and thermodynamic properties of ThC based on the density functional perturbation theory and harmonic approximation.[29]

It is well known that defects are unavoidable in nuclear fuel due to the irradiation damage from high-energy neutrons. However, there are few theoretical works about the defect of ThC. Based on the experimental observations, Matzke[30] wrote a review about the defects for ThC, and he speculated two important points: (i) there are important atomic displacements around carbon vacancies; (ii) there is no indication of antistructure defects in ThC. In our following study, the two conclusions will be verified by us.

Our paper is organized as follows. In Section  2, the calculation details will be described. In Section  3, the calculated results will be presented and discussed. In Section  4, the conclusion remarks will be presented.

2. Calculation methods

All of these calculations were performed within the framework of density functional theory (DFT) and more particularly with the ab initio method[31, 32] as implemented in the Vienna ab initio simulation package (VASP) code.[33] The generalized gradient approximation (GGA) to the exchange-correlation interaction was used.[34] Twelve electrons (6s26p65f06d27s2) for thorium and four electrons (2s22p2) for carbon were taken into account as valence electrons. An energy cut-off of 500  eV for the plane-wave expansion of the electron basis was used. The convergence criteria have been chosen to be 10− 6  eV, and 10− 2  eV/Å for the total energy, and for the forces, respectively. When computing the total energy of a defected structure, the lattice constants were fixed, while the atomic coordinates were allowed to relax. The Brillouin zone is sampled by a 4 × 4 × 4 Monkhorst– Pack k-point mesh[35] for a 64-atoms supercell. The bulk properties of ThC were calculated in a conventional cell which contains four carbon atoms and four thorium atoms with a 16 × 16 × 16 k-point grid being used to sample the Brillouin zone. The calculation of electronic density of states (DOS) and electronic band structure were in a more rigorous condition with an energy cut-off of 600  eV and a 20 × 20 × 20 k-point grid in a conventional cell.

3. Results and discussion
3.1. Bulk properties of ThC

The bulk properties of ThC including the lattice parameters, the bulk modulus, and the electronic properties were calculated from the ab initio method, and compared with the previous theoretical and experimental results. As a whole, the current method with the GGA describes these properties pretty well.

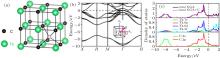
In detail, thorium monocarbide (ThC) has a face-centered cubic lattice as shown in Fig.  1. Our calculated lattice parameter and bulk modulus obtained from the GGA are 5.352  Å and 133.33  GPa, which agree well with the experimental values of 5.335  Å and 125  GPa, respectively. However, the calculated results from the LDA do not fit well with the experiment as shown in Table  1, in particular for the bulk modulus with a relatively large error of 15.9%. Our results demonstrate that the GGA is much better than the LDA. Therefore, the GGA functional is adopted in the rest of this work.

Fig.  1. (a)  Crystal structure of ThC. Black dotted circle represents tetrahedral interstitial site. (b)  Electronic band structure and (c)  total density of state as well as projected density of states of ThC.

The electronic band structure and total DOS as well as projected DOS calculated by GGA are shown in Figs.  1(b) and 1(c), respectively. The total DOS is also calculated by using GGA + U (Ueff = 4  eV), as shown in Fig.  1(c). The profiles of total DOS for these two kinds of methods are almost the same. It means that for the ThC system the strong correlation effect of f orbital electrons can be ignored and the electronic properties can be described sufficiently by using the GGA method. Both Figs.  1(b) and 1(c) show that there is no band gap between the valence and conduction band, indicating that ThC is metal. The electrons around the Fermi level come mainly from Th-5f, Th-6d, and C-2p states, which are mostly located around the Γ point. The conduction band is strongly dominated by Th 5f and Th 6d states, with a little bit of the degree of C 2p states. As for the valence band, the hybridization of C 2p states with the Th 6d states from − 4  eV up to the Fermi energy level contributes to Th-C interaction. Our calculated electronic properties agree well with the previous theoretical results by Aydin et al.[28] Our Bader charge density analysis provides 1.84 electrons charge transfer from Th  atom to C  atom, with respect to their original electron occupation. In the previous calculation of uranium monocarbide UC, [8] a Bader charge transfer of 1.6 electrons occurs from U atom to C  atom. The relatively larger charge transfer value of ThC reflects that the carbon atom takes more electrons away from thorium than uranium.

Table 1. Calculated equilibrium lattice parameters a and bulk modulus B of ThC. Δ a and Δ B are the relative errors of calculated results compared with the experimental values.
3.2. Single point defects and complex defects

We mainly study five types of point defects including vacancy defect, interstitial defect, antisite defect, schottky defect, and composition-conserving defect. To calculate the defect formation energy of single point defects, we use the following formula for one vacancy (VX) or one interstitial defect (IX) (where X labels thorium or carbon defect). The formation energies 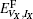are

where EN is the energy of the defect-free ThC supercell, EVX, IX is the energy of the supercell containing corresponding defects, and Ex is the energy per atom of each chemical species in its reference state. Here the reference states are the groundstate crystalline phases of thorium and carbon, namely, the α -thorium crystal and the carbon graphite phase.

As we know that a point defect would interact with its image in the adjacent supercell because of the periodic boundary conditions in our calculation method. Therefore, five different supercell sizes were tested to check the convergence of the formation energy including 1 × 1 × 1 (8  atoms), 2 × 1 × 1 (16 atoms), 2 × 2 × 1 (32  atoms), 2 × 2 × 2 (64 atoms), and 3 × 2 × 2 (96  atoms). Two types of interstitial defects including Th tetrahedral interstitial defect (ITh) and C2 dimer defect along the ⟨ 110⟩ direction were chosen to justify the convergence as illustrated in Table  2. The table shows that the difference in the formation energy for the ITh between a 64-atom and a 96-atom supercell is 0.117  eV. Therefore, we conclude that the calculated formation energies are well converged in a 64-atoms supercell. Eventually, the 64-atoms supercell will be taken in our remaining calculations.

Table 2. Formation energies (eV) of Th tetrahedral interstitial defect (ITh) and C2 dimer defect along the ⟨ 110⟩ direction in ThC as a function of the supercell sizes used in the calculation.

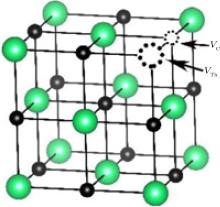
Concerning the single point defects, four types of defects will be considered in our study including single carbon vacancy (VC), single thorium vacancy (VTh), single carbon tetrahedral interstitial (IC) defect, and single thorium tetrahedral interstitial defect (ITh). The tetrahedral site is illustrated in Fig.  1(a), and the calculated formation energies for these defects are listed in Table  3. The table shows that among these defects the carbon vacancy has the lowest formation energy (0.29  eV). This is consistent with the experimental observations, [18, 37] in which the carbon vacancies were considered to be the predominant defects in the nonstoichiometric ThC. It is noted that our result for the carbon vacancy is also in good agreement with the previous result (0.32  eV) by Shein et al., [24] in which this energy was calculated by the full-potential DFT in an eight-atom supercell. The calculated energy for the tetrahedral interstitial carbon (IC) is quite high (3.67  eV), indicating that this kind of defect is almost impossible in ThC. According to Table  3, the carbon vacancy and carbon interstitial defects have lower formation energies than the thorium vacancy and thorium interstitial defects, respectively. This phenomenon is consistent with that in UC, [8] in which the radiation damage and deviation from stoichiometry are more probably generated in the carbon sublattice.

Table 3. Formation energies (Eform) of carbon/thorium vacancy (VC and VTh) and tetrahedral interstitial (ITh and IC) defects, as well as atomic displacements of the first shell (s) and second shell (s) (δ R) due to the presence of point defects in ThC. Negative (positive) value indicates a decrease (increase) of the interatomic distance with relating element symbol in parentheses.

As we know that due to the defects the atomic position will deviate from the original (equilibrium) one. This deviation is defined as the atomic displacements δ R, i.e., changes in atomic separation distance due to the presence of the defect. The displacements for the above four defects were calculated and presented in Table  3. For the single carbon vacancy defect, Table  3 shows that the displacements of the first nearest neighbor (1NN) thorium atoms are in the order of 0.088  Å . This is consistent with the experimental results of ThC1− x obtained by neutron diffraction, [38] which indicates that the displacements of neighboring Th  atoms are in the order of ≈ 2% of the lattice parameter. For the thorium vacancy defect, the displacements of the 1NN atoms of 0.276  Å are induced. For the carbon tetrahedral interstitial defect, Table  3 shows that this causes the inward displacements of carbon atoms of 0.487  Å , and conversely this causes the outwards displacements of the thorium atoms of 0.187  Å . Concerning the thorium tetrahedral interstitial defect, it induces the largest perturbation on its surrounding atoms as shown in Table  3, i.e., the thorium and carbon atoms move outward of 0.531  Å and 0.088  Å , respectively. Actually, this defect also has the largest effect on the second near neighboring (2NN) atoms among the four defects, i.e., the displacements for the defect is 0.132  Å , and the displacements for the other three defects are almost zero.

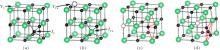
Concerning the complex interstitial defects, we have studied the stabilities of C3 trimer and C2 dimers along different crystallographic orientations as sketched in Fig.  2. Their formation energies are listed in Table  4. The table shows that the C2 dimer along the ⟨ 110⟩ direction has the lowest formation energy of 1.04  eV among these defects. This rationalizes the experimental conclusion that some introduced carbon atoms could link with the existing carbon atoms to form “ C2” groups as high carbon compositions are reached in ThC.[39] It is noted that the energy differences among these defects are small with the largest one being 0.22  eV, suggesting that they could possibly coexist in ThC. Considering the similar energy level between the dimer and the trimer according to Table  4, we can predict that the C3 trimer configuration may be a transition state of the C2 dimer diffusion in ThC. We also present the charge density map of the dimer and the trimer in Fig.  3. The figure shows that it is the carbon– carbon bonding interaction that stabilizes these defects.

Table 4. Formation energies of complex defects, including C2 dimer (C2⟨ 110⟩ , C2⟨ 100⟩ , and C2⟨ 111⟩ ), C3 trimer (C2), antisite defects (CTh and ThC), Frenkel carbon (FPC), Frenkel thorium (FPTh), Schottky (Sch), C2⟨ 100⟩ dimer plus carbon vacancy (C2⟨ 100⟩ + VC), and trimer C3 plus carbon vacancy defects (C3 + VC).

Fig.  2. View of (a) C2⟨ 110⟩ , (b) ⟨ 100⟩ , and (d) ⟨ 111⟩ dimer together with (c) C3 trimer. Th  atoms in green, C  atoms in black. d (C– C) represents the C– C distance of C2 dimer and C3 trimer.

Fig.  3. Charge density distribution graph in (010) plane of ThC for (a)  C2⟨ 110⟩ dimer and (b)  C3 trimer. Red color for high electron density and blue color for low electron density. The contour interval is 0.05 electrons/Bohr3.

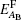
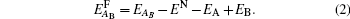
To calculate the defect formation energy of the complex defects, we use the following formulas. For an antisite defect (removing a B atom from its current position and replacing it by an A atom), formation energy reads

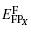
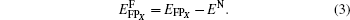
For a bound Frenkel pair, the formation energy reads

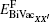
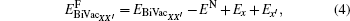
For a bivacancy, the formation energy reads

where EN is the energy of the defect-free ThC supercell, EAB, EFPX, and EBiVacXX' are the energies of the supercell containing corresponding defects, Ex, EA, and EB are the energy per atom of each chemical species in its reference state. Here the reference states are the ground-state crystalline phases of thorium and carbon, namely, the α -thorium crystal and the carbon graphite phase.

The antisite defect is an exchange of one Th and one C  atom in ThC. The calculated formation energies of carbon antisite and thorium antisite are listed in Table  4. The table shows that the energies for the two defects are quite high (larger than 5  eV), indicating that the two defects are unstable. This is in line with the experimental observation, in which the antisite defects were not observed in ThC.[27]

The Schottky defect is a type of electrical neutrality point defect in which an equal number of cations and anions are missing from their lattice sites and the stoichiometry of the crystal is maintained. In ThC, the Schottky defects are resulted from the simultaneous creation of thorium and carbon vacancies as illustrated in Fig.  4. The calculated formation energy for this defect is 4.79  eV as listed in Table  4. This value is lower by about 1.25  eV than the sum of the energies of the isolated thorium and carbon vacancy defects (as listed in Table  3). This phenomenon suggests that the defect will be stabilized when thorium and carbon vacancies are placed as the first neighbor. It is in accordance with the properties of a Schottky defect for UC.[8, 9] Therefore, the widely existing carbon vacancy may aggregate together around the thorium vacancy in ThC.

Since single point defects alone are not compositionconserving, then thermal defects have to appear in balanced combinations in order to maintain the overall composition of ThC crystal. Actually at finite temperature, thermal defects will be activated in ThC. Usually the composition-conserving defects are in pairs of single point defects or in more complex forms.

The most common composition-conserving defect is a Frenkel pair. There are two kinds of common Frenkel defects: one is the carbon Frenkel pair as illustrated in Fig.  5(a), and another is the thorium Frenkel pair as illustrated in Fig.  5(b). The calculated formation energies for the two defects are listed in Table  4. It shows that the energies for the two cases (3.96  eV and 10.14  eV, respectively) are quite high, indicating that the two defects may not exist.

In addition, we have also considered two special types of Frenkel defects: one is a carbon dimer plus a carbon vacancy as indicated in Fig.  5(c), and another is a carbon trimer plus a carbon vacancy as indicated in Fig.  5(d). The formation energies for the two defects are presented in Table  4. Interestingly, the energy for the carbon dimer plus carbon vacancy is as low as 0.49  eV. This value is close to that (0.29  eV) for a single carbon vacancy, indicating that this kind of defect could be stable. This is consistent with the literature view which states that ThC may contain some C2 groups compensated by some carbon vacancies.[40] The energy for the carbon trimer plus carbon vacancy is 1.25  eV which is a little higher than that of the carbon trimer (1.16  eV). The clustering of carbon vacancy and carbon trimer is also favored from the energy point of view at high temperature. In consideration of the existence of the C2 dimer plus the carbon vacancy discussed above, the C3 trimer plus vacancy might be a transition state of the C2 dimer diffusion in ThC.

Fig.  4. The diagram for Schottky defect: the positions of carbon vacancy (VC) and of thorium vacancy (VTh) are indicated by the arrows. Th  atoms in green, C  atoms in black, carbon vacancy and thorium vacancy in black dotted circle.

Fig.  5. (a) Simplified diagram for carbon Frenkel defect: the positions of the carbon vacancy (VC) and of the carbon interstitial (IC) are indicated by the arrows. (b) Simplified diagram for thorium Frenkel defect: the positions of the thorium vacancy (VTh) and of the thorium interstitial (ITh) are indicated by the arrows. (c) Carbon dimer plus carbon vacancy: a carbon vacancy (VC) is formed and a carbon dimer (C2) appears. (d) Carbon trimer plus carbon vacancy: a carbon vacancy (VC) is formed and a carbon trimer (C3) appears. Th  atoms in green, C  atoms in black, carbon vacancy and thorium vacancy in black dotted circle.

4. Conclusions

The defects of thorium monocarbide (ThC) have been studied by means of density functional theory based on the projector-augmented-wave method. Five types of point defects have been considered in our study including the vacancy defect, interstitial defect, antisite defect, schottky defect and composition-conserving defect. Among these defects, the carbon vacancy defect has the lowest formation energy of 0.29  eV. This conclusion is consistent with the experimental phenomenon that the carbon vacancies are the predominant defects in nonstoichiometric ThC. Through the investigation of displacements (δ R) for the single point defects, we have confirmed one experimental speculation that there are important atomic displacements around carbon vacancies. The second most stable defect (0.49  eV) is one of compositionconserving defects in which one carbon is removed to another carbon site forming a C2 dimer (C2 along the ⟨ 100⟩ direction). According to our calculations, we think that the C3 trimer configuration may be a transition state of the C2 dimer diffusion in ThC. Concerning the antistructure defects, our calculations have verified another experimental speculation that there is no antistructure defect in ThC.

Reference
1 Li Q, Yang J S, Huang D H, Cao Q L and Wang F H 2014 Chin. Phys. B 23 017101 DOI:10.1088/1674-1056/23/1/017101 [Cited within:1]
2 Li P, Jia T T, Gao T and Li G 2012 Chin. Phys. B 21 043301 DOI:10.1088/1674-1056/21/4/043301 [Cited within:1]
3 Li L, Wang B T and Zhang P 2015 Chin. Phys. Lett. 32 037102 DOI:10.1088/0256-307X/32/3/037102 [Cited within:1]
4 Sengupta A K, Agarwal R and Kamath S H 2012in Comprehensive Nuclear Materials (ed. R. J. M. Konings) (Oxford: Elsevier) p.  55 [Cited within:1]
5 Lee W E, Gilbert M, Murphy S T and Grime R W 2013 J. Am. Ceram. Soc. 96 2005 DOI:10.1111/jace.12406 [Cited within:1]
6 Shi H, Zhang P, Li S S, Sun B and Wang B 2009 Phys. Lett. A 373 3577 DOI:10.1016/j.physleta.2009.07.074 [Cited within:1]
7 Shi H, Zhang P, Li S S, Wang B and Sun B 2010 J. Nucl. Mater. 396 218 DOI:10.1016/j.jnucmat.2009.11.009 [Cited within:1]
8 Freyss M 2010 Phys. Rev. B 81 014101 DOI:10.1103/PhysRevB.81.014101 [Cited within:3]
9 Ducher R, Dubourg R, Barrachin M and Pasturel A 2011 Phys. Rev. B 83 104107 DOI:10.1103/PhysRevB.83.104107 [Cited within:1]
10 Sahoo B D, Joshi K D and Gupta S C 2013 J. Nucl. Mater. 437 81 DOI:10.1016/j.jnucmat.2013.01.314 [Cited within:1]
11 Carvajal Nuñez U, Martel U L, Prieur D, Lopez Honorato E, Eloirdi R, Farnan I, Vitova T and Somers J 2013 Inorg. Chem. 52 11669 DOI:10.1021/ic402144g [Cited within:1]
12 Berthinier C, Rado C, Dugne O, Cabie M, Chatillon C, Boichot R and Blanquet E 2013 J. Nucl. Mater. 432 505 DOI:10.1016/j.jnucmat.2012.08.002 [Cited within:1]
13 Petti D, Crawford D C and Chauvin N 2009 MRS Bulletin 34 40 DOI:10.1557/mrs2009.11 [Cited within:1]
14 Crawford D C, Porter D L and Hayes S L 2007 J. Nucl. Mater. 371 202 DOI:10.1016/j.jnucmat.2007.05.010 [Cited within:1]
15 Everett III J L and Kohler E J 1978 Ann. Nucl. Energy 5 321 DOI:10.1016/0306-4549(78)90017-8 [Cited within:1]
16 Kleykamp H 1992 Thorium Carbides, Gmelin Hand book of Inorganic and Organometallic ChemistryVol. C6 Berlin Springer [Cited within:2]
17 Kempter C P and Krikorian N H 1962 J. Less Common Met. 4 244 DOI:10.1016/0022-5088(62)90071-1 [Cited within:1]
18 Satow T 1967 J. Nucl. Mater. 21 255 DOI:10.1016/0022-3115(67)90176-6 [Cited within:2]
19 Gerward L, Olsen J S, Benedict U, Itie J P and Spirlet J C 1986 J. Appl. Crystallogr. 19 308 DOI:10.1107/S0021889886089318 [Cited within:1]
20 Yamawaki M, Koyama T and Takahashi Y 1989 J. Nucl. Mater. 167 113 DOI:10.1016/0022-3115(89)90431-5 [Cited within:1]
21 Yamawaki M 1991 Solid State Ionics 49 217 DOI:10.1016/0167-2738(91)90089-T [Cited within:1]
22 Shein I R, Shein K I and Ivanovskii A L 2006 J. Nucl. Mater. 353 19 DOI:10.1016/j.jnucmat.2006.02.075 [Cited within:2]
23 Shein I R, Shein K I, Shveikin G P and Ivanovskii A L 2006 Dokl. Phys. Chem. 407 106 DOI:10.1134/S0012501606040075 [Cited within:1]
24 Shein I R and Ivanovskii A L 2010 Solid State Sci. 12 1580 DOI:10.1016/j.solidstatesciences.2010.07.003 [Cited within:1]
25 Shein I R and Ivanovskii A L 2010 Phys. Solid State 52 2039 DOI:10.1134/S1063783410100069 [Cited within:1]
26 Das T, Deb S and Mookerjee A 2005 Physica B 367 6 DOI:10.1016/j.physb.2005.05.041 [Cited within:1]
27 Lim I S and Scuseria G E 2008 Chem. Phys. Lett. 460 137 DOI:10.1016/j.cplett.2008.06.008 [Cited within:2]
28 Aydin S, Tatar A and Ciftci Y O 2012 J. Nucl. Mater. 429 55 DOI:10.1016/j.jnucmat.2012.05.038 [Cited within:2]
29 Pérez D, Jaroszewicz S, Llois A M and Mosca H O 2013 J. Nucl. Mater. 437 135 DOI:10.1016/j.jnucmat.2013.01.350 [Cited within:2]
30 Matzke H 1984 Solid State Ionics 12 25 DOI:10.1016/0167-2738(84)90128-0 [Cited within:1]
31 Blöchl P E 1994 Phys. Rev. B 50 17953 DOI:10.1103/PhysRevB.50.17953 [Cited within:1]
32 Kresse G and Joubert D 1999 Phys. Rev. B 59 1758 DOI:10.1103/PhysRevB.59.1758 [Cited within:1]
33 Kresse G and Furthmüller J 1996 Phys. Rev. B 54 11169 DOI:10.1103/PhysRevB.54.11169 [Cited within:1]
34 Perdew J P, Jackson K A, Pederson M R, Singh D J and Fiolhais C 1992 Phys. Rev. B 46 6671 DOI:10.1103/PhysRevB.46.6671 [Cited within:1]
35 Monkhorst H J and Pack J D 1976 Phys. Rev. B 13 5188 DOI:10.1103/PhysRevB.13.5188 [Cited within:1]
36 Benz R and Naoumidis A 1987 Thorium Compounds with Nitrogen, Gmelin Hand book of Inorganic ChemistryVol. C3 Berlin Springer [Cited within:1]
37 Lightstone J B and Libowitz G G 1969 J. Phys. Chem. Solids 30 1025 DOI:10.1016/0022-3697(69)90357-6 [Cited within:1]
38 Moisy-Maurice V, de Novion C H and Convert P 1980 Acta Crystallogr. A 36 916 DOI:10.1107/S056773948000191X [Cited within:1]
39 Murch G E and Thorn R J 1979 J. Nucl. Mater. 82 430 DOI:10.1016/0022-3115(79)90025-4 [Cited within:1]
40 Manara D, De Bruycke F, Sengupta A K, Agarwal R and Kamath H S 2012in Comprehensive Nuclear Materials (ed. J. M. K. Rudy) (Oxford: Elsevier), p.  87 [Cited within:1]