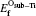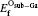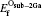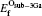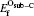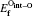†Corresponding author. E-mail: duanws@nwnu.edu.cn
*Project supported by the National Magnetic Confinement Fusion Science Program of China (Grant No. 2014GB104002), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA03030100), and the National Natural Science Foundation of China (Grant Nos. 11275156 and 11304324).
This paper presents the mono-vacancy formation and migration energies of each element Ti, Ga, and C in the MAX phase Ti2GaC, which are obtained by first principles calculations. We also calculate the formation energies of oxygen substituting for Ti, Ga, and C and two formation energies of oxygen interstitial in different sites. The results show that the formation energy of oxygen substituting for Ti is the highest, and the formation energies of the O substitution for Ga atoms decrease as the oxygen concentration increases. The two different formation energies of one oxygen interstitial show that the stable site for the oxygen interstitial is at the center of the triangle composed by three Ga atoms. The effects of vacancy, oxygen substitution, and the interstitial on the electronic properties of Ti2GaC are also discussed in light of the density of states and the electron charge density.
The MAX phases (Mn+ 1AXn, where n = 1, 2, 3, M is an early transition metal, A is an A-group element, mostly from groups IIIA and IVA, and X is either carbon or nitrogen) form a broad family of ternary compounds, which combine metallic and ceramic properties because they consist of alternating layers with metallic (MA) and covalent bonding (MX).[1– 5] They possess remarkable properties, such as the exceptional thermal shock resistance and damage tolerance, excellent oxidation resistance, and elastic stiffness. Therefore, the MAX phases have been considered as high-temperature structural materials with a number of potential applications, especially in the nuclear industry. For example, Ti– Al– C system and Ti– Si– C system compounds have been proposed as candidate materials for structural and fuel coating applications in future fission and fusion reactors, [6– 8] other possible applications include Ohmic contacts to SiC, which already exists commercially.[9, 10] Consequently, the search for new MAX phases with improved properties is of great interest. As one of the important MAX phases, single crystal of Ti2GaC was synthesised by the powers Ti, C, and Ga, which were mixed in a ratio of 5:2:7 and pressed into a pellet. The pellet was put into a corundum crucible and quickly (200 K/h) heated to 1500 ° C under an argon atmosphere. The small hexagonal platelets were identified as Ti2GaC, and the hexagonal unit cell was indexed by x-ray diffraction (XRD) pattern with a lattice parameters a = 3.063(4)Å and c = 13.312(2)Å .[11, 12] The structural, elastic, electronic, and thermodynamic properties of Ti2GaC have been investigated.[1, 13– 21]
As is well known, in the fusion reactor, the nuclear materials encounter a strong flux of 14-MeV neutrons and high-energy particle irradiation. They subsequently experience a variety of transmutations and radiation damage which is induced by the interaction with the neutrons. Excellent nuclear materials must have a good ability to withstand irradiation damage. Irradiation damage produces various kinds of crystal defects, so the behavior of the point defect plays a key role in the damage of materials.[22, 23] Both the defect formation and their interaction can modify the physical properties and the growth behavior in irradiated environments, long-term endurance, crystal growth, thin-film deposition of MAX phases at high temperatures or in corrosive environments, etc.[24– 27] Vacancies are the dominant intrinsic defects in materials. For MAX phases, interaction with oxygen, especially the incorporation of oxygen in the initial stages of oxidation, is essential in understanding and improving the performance.[27] Oxygen dissolution is also important for the design of self-healing MAX phases.[28– 30]
The present paper studies the defect-related properties of MAX phase Ti2GaC. The mono-vacancy formation and migration energies of Ti, Ga, and C in Ti2GaC are obtained by first principles calculations. Additionally, in order to explore the phase stability of oxygen-containing Ti2GaC, we have calculated the formation energies of oxygen substitution and the interstitial. This is relevant to the high temperature performance of MAX phases, since oxygen dissolution may affect the nucleation of meta-stable oxides during oxidation. Finally, the effects of vacancy, oxygen substitution, and the interstitial on the electronic properties of Ti2GaC have also been discussed by density of states (DOS) and the electron charge density (ECD).
Theoretical investigations have been undertaken by using the plane-wave pseudopotential total energy calculation method that is based on the framework of density functional theory (DFT), which is implemented in the CASTEP code.[25, 31] The plane wave energy cutoff and the Brillouin zone sampling are fixed to 450 eV and 7 × 7 × 3 special k-point meshes, respectively. The electronic exchange– correlation energy is treated under the generalized gradient approximation in the Perdew– Burke– Ernzerhof (GGA-PBE) scheme.[25]
The mono-vacancy structure of Ti2GaC is represented by a 2 × 2 × 1 supercell containing 31 atoms after removing one atom from the MAX phase. The mechanism of mono-vacancy migration is actually self-diffusion of the corresponding atom, and the migration energies are calculated by assuming that the self-diffusion is taking place in a neighboring vacancy, which is reserved to jump along the [0001] plane. The migration energy Em is calculated by investigating the transition state linking the two end defective configurations, and is given as follows:
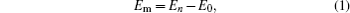
where En is the total energy of the transition state (saddle point) along the reaction path in a Ti2GaC system. E0 represents the lowest total energy of the same system at one of the end points of the reaction path. The linear synchronous transit (LST) or quadratic synchronous transit (QST) method is used along with a conjugate gradient (CG) algorithm when determining the migration barriers.
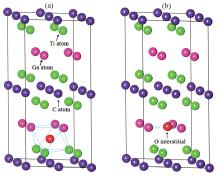
The formation energies of oxygen substitution are obtained by substituting an oxygen atom for atom in Ti2GaC. The oxygen interstitial is considered in two different conditions, namely: occupying the octahedral site in Ti2GaC and at the center of the triangle composed by three Ga atoms, as shown in Fig. 1, which are thought as a stable structure that has an interstitial.[32– 35]
The formation energy of a neutral defect Ef[X] is defined as follows:[36– 38]

where Etot[def] is the total energy of the Ti2GaC with the defect X, and Etot[bulk] is the total energy of the bulk Ti2GaC. ni indicates the number of atoms of type i (host atoms or impurity atoms) that have been added to (+ ) or removed from (− ) the Ti2GaC supercell to form the defect, and the μ i are the corresponding chemical potentials of these species. The chemical potentials of pure phases depend on pressure and temperature. In our study, the reference state of chemical potentials of Ti, Ga, and C elements, namely upper bounds, are set by the formation of metallic Ti, Ga, and diamond C, respectively,
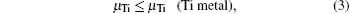

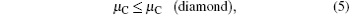
which represent their corresponding rich conditions. Combining with Eqs. (2)– (5), the lower bounds of these chemical potentials are a representation of their poor conditions:
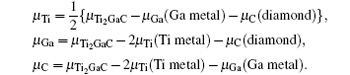
While for the strong dependence of the chemical potential of gases O2 on temperature and partial pressure, the reference state chemical potential of O (μ O) is regarded as
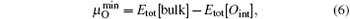
the Etot[Oint] represents the total energy of bulk Ti2GaC containing an interstitial of oxygen atom.
The calculated equilibrium values of the structure parameters of defective supercell with a Ti, Ga, and C vacancy in Ti2GaC are presented in Table 1 together with the experimental results. For the lattice parameters of a and c, the results are consistent with the previously experimental work, which ensures the reliability and accuracy of the present first-principles calculations. It is noted from Table 1 that the lattice parameter a increases for a Ti or Ga vacancy and decreases for a C vacancy existence in Ti2GaC. However, the lattice parameter c decreases when there is a Ga vacancy, while the opposite results are observed when there is a Ti or C vacancy. In addition, the crystal would be compressed if there is a Ga or C vacancy but expanded for a Ti vacancy in Ti2GaC compound. These calculated results explain the crystal distortions under high-temperature and in an irradiation environment in the presence of vacancies defects.
| Table 1. Calculated lattice paraments and unit cell volume. |
The calculated partial electronic density of states (PDOS) of defect-free Ti2GaC is shown in Fig. 2. The DOS can provide a valuable insight to understand the nature of the atomic bonding which control the structural properties of Ti2GaC. It should be stressed that d-orbital energy of transition metals under traditional DFT calculations is underestimated, so we also use the precise calculations method (DFT+ U). In Fig. 2, panel (a) is the result of DFT calculation, panel (b) is the result of DFT+ U (U = 2) calculation. By comparing panels (a) and (b), we find that the results of the two cases are very similar, which confirms our conclusion. It is observed from Fig. 2 that Ti’ s d orbital contributes the most to the DOS around the Fermi level, the contribution of Ga around Fermi level is slight, and it is almost negligible for the contribution of C element. We also observed the strong hybridization between the Ti’ s d-orbital and C’ s p-orbital in the range − 4 eV to − 3 eV, which indicates a strong interaction between Ti and C. The overlap between Ti’ s d-orbital and Ga’ s p-orbital at − 1.2 eV suggests the existence of Ti– Ga metallic bond. However, the Ti– C covalent bond is stronger than the Ti– Ga metallic bond because the hybridization peak of Ti– C is higher.
 | Fig. 2. The PDOS and TDOS of defect-free Ti2GaC: panel (a) is the result of DFT calculation, panel (b) is the result of DFT+ U calculation. |
Figure 3 shows the results of the vacancy formation energies as functions of the atomic chemical potential of each component in Ti2GaC. As noticed from Fig. 3, Ti vacancy is recognized as the most unlikely vacancy species for every available chemical potential. The formation energies are 3.013 eV (Ga-rich) and 3.047 eV (C-rich) for a Ga and C vacancy, respectively. The variable ranges of chemical potentials for Ga and C atoms are almost the same. Therefore, their formation energies in corresponding poor conditions are − 1.577 eV and − 1.546 eV, respectively. These results suggest that the Ga and the C vacancies are more likely to exist compared with the Ti vacancy. Ti2AlC[24] and Nb2 GeC[39– 42] has a common characteristic with Ti2GaC in that the formation energies for Al and C vacancies are almost equal, but the specific energy values are relatively low. It is also inferred that Ti2GaC has good performance under extreme conditions, such as high-temperature and irradiation environment.
 | Fig. 3. The mono-vacancy formation energies, as a function of the atomic chemistry potential of each component in Ti2GaC. |
The calculated energy barriers of Ti, Ga, and C vacancy migration energies along the [0001] plane are 2.459 eV, 1.399 eV, and 3.152 eV, respectively. It is noted that the Ga vacancy is the most energetically favorable to form, which is in agreement with the other theoretical results. The A-group element atoms are easily outward diffusing and they determine the key properties of the MAX phases compounds.[24] For instance, the migration energy of Al vacancy along the [0001] plane in Ti2AlC is 0.83 eV, which is the lowest value compared with that of Ti (2.38 eV) and C (3.00 eV) vacancies. As confirmed by the experiment results, the Al atoms easily diffuse towards the surface and form an Al2O3 protective layer to prevent oxygen oxidation.[24, 43] We can also speculate that the Ga2O3 compound was formed in Ti2GaC because of the Ga atoms that can easily be diffused outward. We expect that the related experiments can prove our calculated results.
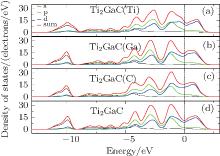 | Fig. 4. (a) The DOS of Ti2GaC with a Ti vacancy, (b) the DOS of Ti2GaC with a Ga vacancy, (c) the DOS of Ti2GaC with a C vacancy, (d) the DOS of Ti2GaC without vacancy. |
The DOS of Ti2GaC with mono-vacancy Ti, Ga, and C is shown in Fig. 4. It seems that the hybridization bonding has not been changed much, which suggests that Ti2GaC with mono-vacancy can remain in a stable structure. However, slight changes can still be observed from Fig. 4. Compared with the peak of hybridization of defect-free supercell at − 1.2 eV, the peak of hybridization of Ti2GaC with Ti vacancy is smaller, and the energy level of Ti’ s 3d state electrons shifts towards the Fermi level. Both of these changes infer that the strength of Ti– Ga bond weakens. Similarly, the interaction between Ti and C also weakens. As for Ga and C vacancies, they have little impact on the the peak of hybridization, which means that they have a slight effect on the electronic and structural properties. These results are in agreement with the three mono-vacancy formation energies, Ti vacancy which has the greatest effect on electronic property has the highest formation energy, and the Ga and C vacancies have little impact on the electronic properties, so their formation energies are low.
In this section we will investigate O atom substituting for Ti, Ga, and C atoms, respectively. The formation energies of these substitutions, as functions of the O atomic chemical potential, are shown in Table 2. The Osub– Ti, Osub– Ga, and Osub– C represent the O atom substitution for the Ti, Ga, and C atoms, respectively. The Osub– 2Ga and Osub– 3Ga represent the two and three O atoms substitution for the same numbers of Ga atoms. Meanwhile, the Oint– O and Oint– T represent an oxygen interstitial occupying the octahedral and triangle sites, respectively, as shown in Fig. 1. As can be seen from Table 2, the formation energies of an O atom substituting for Ti and C atoms in the O-rich condition are 3.798 eV and − 3.332 eV, respectively. While they are 5.723 eV and − 1.408 eV in the O-poor condition. It is noted that the O atom prefers to substitute for the C atom because the chemical properties of oxygen are more similar to carbon than titanium. The Osub– Ga, Osub– 2Ga, and Osub– 3Ga formation energies are − 0.424 eV, − 2.366 eV, and − 7.61 eV in O-rich condition, respectively. Their formation energies are 2.349 eV, − 0.441 eV, and − 5.686 eV in O-poor condition, respectively.
We note from these results that the formation energies of the O substitution for Ga atoms decrease as the oxygen concentration increases.
Table 2. The formation energies  |
We also observe that O atom prefers to get close to A layer rather than to occupy the position of Ti vacancy if O atom substitutes for Ti atom. The bond length of Ga– O is 1.983 Å , while that of the Ti– O is 1.919 Å . The Ga– O bond length in Ga2O3 is 1.832 Å , [44] while that of the Ti– O in TiO2 is 1.949Å .[21, 45] We can infer that the TiO2 is possibly formed if the oxygen incorporates into the Ti2GaC compound since the bond length is very close to the TiO2. We must note that all the calculated results are in the condition of 0 K, while the experimental results are not at 0 K. Therefore, the comparison is never straightforward. There is some slight position deviation between O atom and Ga vacancy in the condition that Ga atom is substituted. However, the O atom occupies the site of C vacancy absolutely.
The DOS of Ti2GaC after substitution by O is shown in Fig. 5. It is noted that the range of the Ti d-orbital and C s-orbital hybridization is broadened and shifts towards the right when a Ti atom is substituted by O. When a Ga atom is substituted by O, we can find a larger peak of p state electrons at the point of − 7.3 eV, which derives from O-2p electrons, and can find a broad pseudo-gap, which infers that the structure is relatively stable, this conforms its lower formation energy. When C is substituted by O, the change of DOS is not obvious, except that the Fermi lever shifts towards right. The reason for this may be that the chemical property of oxygen is similar to carbon.
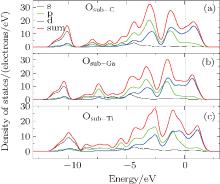 | Fig. 5. The DOS of Ti2GaC with an oxygen substituting carbon, (b) the DOS of Ti2GaC with an oxygen substituting gallium, (c) the DOS of Ti2GaC with an oxygen substituting titanium. |
The formation energies for octahedral and Ga-layer triangle configurations are listed in Table 2. These kinds of interstitial sites can cause crystal distortion and lattice constant change after structure relaxation. For the octahedral site, the formation energies of the oxygen interstitial are − 1.925 eV under O-rich condition and − 3.8498 eV under O-poor condition, respectively. Meanwhile, the formation energies of oxygen interstitial for Ga-layer triangle configuration are − 2.389 eV under O-rich condition and − 4.3138 eV under O-poor condition, respectively. We note that the formation energies are negative in any case of the chemical potential, which means that the oxygen interstitial is easy to form in Ti2GaC. The formation energies for Ga-layer triangle configuration are lower than those in the octahedral configuration. Therefore, the oxygen interstitial prefers to bind with the neighboring Ga atoms and then form the gallium oxide (Ga2O3) semiconductor, which is similar to the feature of other MAX phase materials. The A layers are easy to be oxidized and to form oxide, such as Al2O3 and Cr2O3 compounds.[43, 46]
The electron charge density (ECD) is used to analyze the bonding character in Ti2GaC. The ECD of Ti2GaC with an oxygen interstitial occupying the octahedral site is shown in Fig. 6. In the connection between Ti and O atoms, a high ECD distribution (0.475) centers the middle of the bond, while in the connection between Ga and O atoms, the ECD has a significant reduction compared with Ti and O, which indicates that the Ti– O bond is stronger than the Ga– O bond. This is verified by the Mulliken population analysis, from which we can observe that the charge transferred from the O atom to its three neighboring Ti atoms is 0.09 electrons, respectively, and the charge for O atom obtained from three neighboring Ga atoms is 0.07 electrons. It can also be observed that Ti– O population is 0.32 and Ga– O population is − 0.04, which indicates that they are covalent bond and ionic bond, respectively. We can observe that the interaction between Ti atom and Ga atom is very strong from Fig. 6, so it is easier to insert an atom among Ga atoms than among Ti atoms and Ga atoms, which is consistent with the results of the interstitial formation energy.[47– 50]
This paper presents the mono-vacancy formation and migration energies of each element Ti, Ga, and C in Ti2GaC, which are obtained by first principles calculation. The formation energy of Ga vacancy is the lowest among the three mono-vacancy formation energies since the A element is very mobile. The migration energy of Ga vacancy is the lowest of the three mono-vacancy migration energies, which means that the migration of the Ga vacancy is the easiest migration in Ti2GaC. Furthermore, the formation energies of oxygen substitution and the interstitial are obtained. It is noted that the structure of O substitution for C is the most stable, and the O interstitial prefers to incorporate at the center of the triangle composed by three Ga atoms. By combining migration energy of Ga vacancy with the length of Ga– O bond, we can speculate that Ga atom migrates towards the surface to form Ga2O3. It is noted that the vacancy of each element has a slight effect on the hybridization bonding, a Ti vacancy can affect the Ti– C bonding and Ti– Ga bonding. For oxygen substitution and interstitial, the new chemical bonds Ti– O and Ga– O are found, and the Ti– O bond is stronger.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|