Cite this Article
Zheng Long†, Zhu Xiao-Qin, Sui Yong-Xing, Xue Jian-Zhong, Liu Bo, Pei Ming-Xu. Structure and chemical valence study of Sr n+1Ru nO3 n+1 ( n = 1, 2, ∞) series . Chinese Physics B, 2015, 24(5): 056101  
Permissions
Structure and chemical valence study of Sr n+1Ru nO3 n+1 ( n = 1, 2, ∞) series
Zheng Long†, Zhu Xiao-Qin, Sui Yong-Xing, Xue Jian-Zhong, Liu Bo, Pei Ming-Xu
School of Mathematics and Physics, Jiangsu University of Technology, Changzhou 213001, China

†Corresponding author. E-mail: zhengphy@163.com

Abstract

Effect of structure parameter n and its coupling with the connection mode among RuO6 octahedra of Sr n+1Ru nO3 n+1 ( n = 1, 2, ∞) are investigated. The gradually enhanced rotation and tilting effect with increasing n are observed in Sr n+1Ru nO3 n+1. Besides, the chemical valence of Ru is not changed, while the one of Sr gradually varies with increasing n, which highlights the great contribution of connection mode to the chemical environment. Our results show a strong n dependence on the connection mode between octahedra in Sr n+1Ru nO3 n+1 ( n = 1, 2, ∞).

Keyword: 61.05.cp; 78.70.Ck; ruthenates; structure parameter; x-ray diffraction; extended x-ray absorption fine structure
1. Introduction

The peroviskite-like strontium ruthenates Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ), where n is the number of layers of corner-sharing RuO6 octahedra per formula unit, display a remarkable array of complex electronic and magnetic properties.[1] SrRuO3 (n = ∞ ) is an itinerant ferromagnet.[2] Bilayered Sr3Ru2O7 (n = 2) is identified as an enhanced paramagnet.[3] Single-layer Sr2RuO4 (n = 1) is an unconventional superconductor.[4] Specifically, Srn+ 1RunO3n+ 1 exhibits strong dependence on the number n, reflecting the high level of strong structure parameter n control effect in this system.

It is believed that the octahedra of RuO6 in Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ), which exhibits a delicate balance among RuO6 octahedra, [5] is the origin of those intriguing physical properties.[6] The distortion of octahedron, such as the size, shape, and connection mode among octahedra, tends to have a profound influence on the ground state.[7] As the RuO6 octahedra in these crystals have very similar size, [8] the property can thus be greatly tuned by the connection mode. The change of n, which reflects the number of Ru– O layers, will modify the connection mode of octahedra. Because it is crucial to study the modulation of the connection mode changed by n, a deeper understanding of the properties of these ruthenates may be developed.

In this paper, we focus on the layered system of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) series. The coupling between structure parameter n and connection mode among RuO6 octahedra is investigated using the x-ray diffraction (XRD) and extended x-ray absorption fine structure (EXAFS) methods. With n increasing, the rotation effect and tilting effect (Fig.  1(d)) are detected[9, 10] and the chemical valence of Sr is changed. There is a strong n dependence on the connection mode among octahedra in layered Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) series.

Fig.  1. Schematic illustration of the unit cells of (a) Sr2RuO4 with space group I4/mmm, (b) Sr3Ru2O7 with space group I4/mmm, and (c) SrRuO3 with space group Pnma. (d) Schematic illustration of the rotation (upper) and tilting (down) effect between RuO6 octahedra. Ru ions are in the center of each octahedra.

2. Experimental

Single-phase polycrystalline Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) samples were synthesized by a conventional solid-state reaction method. The crystal structure was confirmed by XRD using Rigaku Dmax-rB diffractometer. All XRD data were collected in a step mode with an interval of 0.02° in 2θ range of 10° < 2 θ < 70° . The crystal structure analysis was performed using the Rietveld refinement method. [11] The x-ray absorption data at Ru K-edge for all samples were recorded at room temperature in transmission mode at beamline BL14W1 in the Shanghai Synchrotron Radiation Facility (SSRF), China. The EXAFS data were processed using ATHENA, and the structural parameters were obtained using the code of IFEFFIT.[12] The x-ray photoelectron spectroscopy (XPS) measurements were carried out by PHI 5000 VersaProbe with Al Kα x-ray source. The temperature dependence of resistivity was measured by the standard four-probe method.

3. Results and discussion

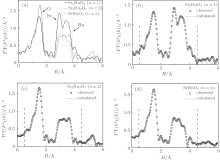
We define n (n = 1, 2, ∞ ) as the number of Ru– O layers, which are composed of corner sharing Ru– O octahedral (see Fig.  1). The Sr2RuO4 (n = 1) has a single Ru– O layer (see Fig.  1(a)), and Sr3Ru2O7 (n = 2) has double coupled Ru– O layers (see Fig.  1(b)) and SrRuO3 (n = ∞ ) is a distorted perovskite with a continuous stack of Ru– O layers (see Fig.  1(c)). In order to investigate the effect of structure parameter n on the property, we perform detailed structure analysis. The x-ray diffraction measurement reveals that all Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) samples are of single phase. The refinement results for all samples are compared with that of experimental data. As can be seen from Fig.  2, the refinement results are of high quality with Rwp factor lower than 7%. The calculated lattice parameters a, b, c, volumes, and Ru– O– Ru angles are summarized in Table  1.

Fig.  2. x-ray diffraction data (line) and calculated data (× ) for the samples (a) Sr2RuO4 with space group I4/mmm, (b) Sr3Ru2O7 with space group I4/mmm, and (c) SrRuO3 with space group Pnma. Marks with short bar (| ) indicate the positions of Bragg reflections, and the difference between observed and calculated data are in the bottom.

Table 1. Calculated lattice parameters a, b, c, volumes, and Ru– O– Ru angles of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) from structure refinement.

As can be seen from Table  1, with increasing n, the space group of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) evolves from I4/mmm to Pnma. Besides, the Ru– Oab-Ru angle, which represents the rotation effect between octahedra (see Fig.  1(d)), [13] gradually decreases with n, indicating the enhanced rotation effect, while the tilting effect between octahedra (see Fig.  1(d)) is lost in structure with I4/mmm symmetry. Although the structure calculation with space group I4/mmm for Sr3Ru2O7 is of high quality, Kiyanagi et al. indicated that Sr3Ru2O7 may prefer a lower symmetry space groups with slight tilting effect.[14] However, the titling angle is so small that it cannot be detected using a refinement method.

The x-ray absorption fine structure (XAFS) technique is suitable for solving this problem. The XAFS enables one to acquire information on the local environment of each element in the material under investigation. As a result, the XAFS is especially attractive for studying the structure near core atoms, especially the distance between core atom and neighbor atoms. Figure  3 shows the normalized XAFS spectra at Ru– K edge for samples of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ). The absorption edge of the x-ray absorption near edge structure (XANES) spectrum is expected to shift when the valence state of manganese is altered.[15] Nevertheless, the shift of x-ray absorption spectra of our samples has not been detected here, demonstrating that the chemical valence of Ru is not changed with increasing n. It can be concluded that the chemical environment around Ru ions (in RuO6 octahedra) remains the same despite increasing n.

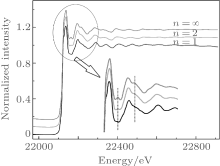Fig.  3. Normalized XAFS spectra at the Ru– K edge for samples of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ). Insert shows the detailed spectra near the absorption edge.

However, the local structure does change with n. As can be seen in the insert of Fig.  3, new small peaks (marked with dashed lines) can be observed with increasing n. The k2-weighted Fourier transform spectra x(k) are shown in Fig.  4(a). The atoms corresponding to each peak are marked in the figure.[16] In Fig.  4(a), with the increase of n, the shape of Ru peaks is clearly changed. This peak gradually splits into two peaks, indicating that there may be two types of Ru– Ru paths in Srn+ 1RunO3n+ 1 when n > 1. This result reveals that the structure parameter n has profound effect on the connection mode between RuO6 octahedra in Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ).

Fig.  4. (a) Fourier transformed spectra from EXAFS data of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) at the Ru K-edge. Insert shows the detailed difference of samples. Atoms corresponding to each peak are marked. (b)– (d) Comparison between the Fourier transformed EXAFS spectra and the fitted curves. The ranges between the two vertical dash lines are the fitting ranges.

To better understand the connection mode evolution of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ), EXAFS data need to be calculated. The Ru– Ru distances are obtained using the Fourier transform data, over the range of 0.6– 4.6  Å . Fitting curves are shown in Figs.  4(b)– 4(d). It is seen that the observed data and calculated data match very well with the R factor below 0.002. The calculated Ru– Ru distance, Debye– Waller factors σ 2, and the coordination number N*amp, are shown in Table  2. Two types of Ru– Ru paths are observed in Sr3Ru2O7 (n = 2) and SrRuO3 (n = ∞ ). Ru– Ru path in the c direction represents the Ru– Ru distance between corner-sharing RuO6 octahedra in the c direction, while Ru– Ru path in the ab plane represents the distance at the Ru– O plane.

Table 2. Calculated Ru– Ru distance, Debye– Waller factors σ 2, and the coordination number N*amp of Ru K-edge EXAFS data for Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ).

In Sr2RuO4 (n = 1), only one scattering path of Ru– Ru can be observed, while two paths of Ru– Ru are achieved in Sr3Ru2O7 (n = 2) and SrRuO3 (n = ∞ ) in the fitted range. As the RuO6 octahedra in these crystals have very similar size, the evolution of the Ru– Ru distance should be attributed to the rotation and tilting effect between RuO6 octahedra. The Ru– Ru distance L in Sr2RuO4 (n = 1) is longer than that in Sr3Ru2O7 (n = 2) and SrRuO3 (n = ∞ ), namely, L(n = 1) > L(n = 2) > ( n = ∞ ). This result puts forward a direct consequence that the rotation and tilting effect is gradually enhanced with increasing n.

In addition, the Ru– Ru distance difference between the two paths is 0.105  Å in Sr3Ru2O7 (n = 2) and 0.117  Å in SrRuO3 (n = ∞ ), respectively. The increased difference, 0.105  Å (n = 2) and 0.117  Å (n = ∞ ), once again reveals the gradually enhanced rotation and tilting effects with increasing n. The structure parameter n can effectively tune the connection mode between RuO6 octahedra. Rotation and tilting effects between RuO6 octahedra arise with increasing n. Strictly, Sr3Ru2O7 prefers a lower symmetry space groups with tilting effect involved, instead of I4/mmm. Our calculated Ru– Ru distances show clear n dependence, supporting this scenario well.

The evolution of connection mode with increasing n should result in the change of chemical environment. The XAFS result reveals that the chemical valence of Ru is not changed. As a result, the bond environment of Sr and O may be changed with n. The XPS has been widely used to study the chemical environment. Figure  5 shows the Sr 3d core-level XPS spectra of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ). As can be seen, the 3d peak position gradually moves to lower binging energy. The behavior is different from previous result, [17] which may result from the oxygen non-stoichiometry in Srn+ 1RunO3n+ 1 due to the solid-state reaction method.

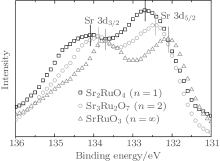Fig.  5. Sr 3d core-level XPS spectra of Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ). The peak positions are marked by the solid bars.

The n dependence of electrical resistivity ρ (T) is measured and shown in Fig.  6. The Sr2RuO4 (n = 1) shows semiconducting behavior, while Sr3Ru2O7 (n = 2) and SrRuO3 (n = ∞ ) show metallic property. Still, the semiconducting behavior in Sr2RuO4 stems from the oxygen non-stoichiometry.[18] A clear anomaly can be observed in Fig.  6(c), suggesting that the effect of magnetic transition becomes more significant as the dimensionality decreases.

Fig.  6. Resistivity of Srn+ 1RunO3n+ 1 ((a) n = 1, (b) n = 2, (c) n = ∞ ) as a function of temperature. The arrow indicates the Curie transition.

4. Conclusions

In this study, the structure and chemical valence in Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) are investigated. In Sr2RuO4 (n = 1), only the rotation effect is observed. Two scatting paths of Ru– Ru can be observed in Sr3Ru2O7 (n = 2) and SrRuO3 (n = ∞ ), indicating the coexistence of the rotation and tilting effects in the structure. Gradually enhanced rotation and tilting effects with increasing n are observed. With the evolution of the connect mode, chemical valence of Sr is changed. There is a strong n dependence in the change of connection mode between octahedra in Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ), which is the origin of the abundant property in Srn+ 1RunO3n+ 1 (n = 1, 2, ∞ ) series.

Acknowledgments

We are grateful to the Jiangsu University of Technology for financial support. The authors also thank beamline BL14W1 at SSRF for providing the beam time.

Reference
1 Ke X, Peng J, Tian W, Hong T, Zhu M and Mao Z Q 2014 Phys. Rev. B 89 220407 DOI:10.1103/PhysRevB.89.220407 [Cited within:1]
2 Gupta K, Mand al B and Mahadevan P 2014 Phys. Rev. B 90 125109 DOI:10.1103/PhysRevB.90.125109 [Cited within:1]
3 Dhital C, Hogan T, Zhou W, Chen X, Ren Z, Pokharel M, Okada Y, Heine M, Tian W, Yamani Z, Opeil C, Helton J S, Lynn J W, Wang Z, Madhavan V and Wilson S D 2014 Nat. Commun. 5 3377 DOI:10.1038/ncomms4377 [Cited within:1] [JCR: 10.015]
4 Stricker D, Mravlje J, Berthod C, Fittipaldi R, Vecchione A, Georges A and van der Marel D 2014 Phys. Rev. Lett. 113 087404 DOI:10.1103/PhysRevLett.113.087404 [Cited within:1] [JCR: 7.943]
5 Malvestuto M, Carleschi E, Fittipaldi R, Gorelov E, Pavarini E, Cuoco M, Maeno Y, Parmigiani F and Vecchioneet A 2011 Phys. Rev. B 83 165121 DOI:10.1103/PhysRevB.83.165121 [Cited within:1]
6 Carlo J P, Goko T, Gat-Malureanu I M, Russo P L, Savici A T, Aczel A A, MacDougall G J, Rodriguez J A, Williams T J, Luke G M, Wiebe C R, Yoshida Y, Nakatsuji S, Maeno Y, Taniguchi T and Uemura Y J 2012 Nat. Mater. 11 323 DOI:10.1038/nmat3236 [Cited within:1] [JCR: 35.749]
7 Gu M Q, Xie Q Y, Shen X, Xie R B, Wang J L, Tang G, Wu D, Zhang G P and Wu X S 2012 Phys. Rev. Lett. 109 157003 DOI:10.1103/PhysRevLett.109.157003 [Cited within:1] [JCR: 7.943]
8 Cao G, Alexand er C S, McCall S, Crow J E and Guertin R P 1999 Mater. Sci. Engin. B 63 76 DOI:10.1016/S0921-5107(99)00055-0 [Cited within:1] [JCR: 1.846]
9 Peng J, Qu Z, Qian B, Fobes D, Liu T J, Wu X S, Pham H M, Spinu L and Mao Z Q 2010 Phys. Rev. B 82 024417 DOI:10.1103/PhysRevB.82.024417 [Cited within:1]
10 Fang Z Terakura K 2001 Phys. Rev. B 64 020509(R) DOI:10.1103/PhysRevB.64.020509 [Cited within:1]
11 Larson A C and Von Dreele R B 2004 Los Alamos National Laboratory Report LAUR 86 748 [Cited within:1]
12 Ankudinov A L, Ravel B, Rehr J J and Conradson S D 1998 Phys. Rev. B 58 7565 DOI:10.1103/PhysRevB.58.7565 [Cited within:1]
13 Zheng L and Wu X S 2013 Chin. Phys. B 22 107806 DOI:10.1088/1674-1056/22/10/107806 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
14 Kiyanagi R, Tsuda K, Aso N, Kimura H, Noda Y, Yoshida Y, Ikeda S I and Uwatoko Y 2004 J. Phys. Soc. Jpn. 73 639 DOI:10.1143/JPSJ.73.639 [Cited within:1] [JCR: 2.087]
15 Zheng L, Cai J Z, Xie Q Y, Lv B, Mao Z Q and Wu X S 2013 J. Mag. Mag. Mat. 342 115 DOI:10.1016/j.jmmm.2013.04.028 [Cited within:1]
16 Lahiri D, Shibata T, Chattopadhyay S, Singh R S, Sharma S M and Maiti K 2009 J. Phys. : Conf. Ser. 190 012099 DOI:10.1088/1742-6596/190/1/012099 [Cited within:1]
17 Guo H Z, Li Y, Urbina D, Hu B, Jin R Y, Liu T J, Fobes D, Mao Z Q, Plummer E W and Zhang J D 2010 Phys. Rev. B 81 155121 DOI:10.1103/PhysRevB.81.155121 [Cited within:1]
18 Chand rasekaran K, Vijayaraghavan R and Varadaraju U V 1998 Mater. Chem. Phys. 56 63 DOI:10.1016/S0254-0584(98)00140-0 [Cited within:1] [JCR: 2.072]