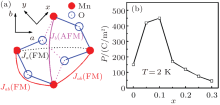
Multiferroics have attracted a great deal of attention over the past decades due to the potential applications and basic physical research interest.^{[1– 3]} Especially, the orthorhombic perovskite rare-earth manganites RMnO₃ (R = Tb, Dy, Eu_{1 − x}Y_x, etc., with the crystal structure on the ab-plane shown in Fig.  1(a)) have been extensively addressed since the discovery of the strong magnetoelectric (ME) coupling in TbMnO₃.^{[4– 6]} The ferroelectric (FE) polarization (P) in RMnO₃ is generated by frustrated spin orders such as the cycloidal spin (CS) order and the E-type antiferromagnetic (E-AFM) order. It is believed that adjacent two spins S_i and S_{i + 1} separated by vector r_{i, i + 1} can generate a local polarization 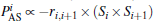through the antisymmetric exchange striction.^{[7– 9]} Thus, a macroscopic polarization P_AS is induced along the a-axis (P_AS//a) in the ab-plane cycloidal spin (ab-CS) phase with the propagation vector along the b-axis, while it is induced along the c-axis (P_AS//c) in the bc-plane cycloidal spin (bc-CS) phase. On the other hand, the very large P_S along the a-axis induced in the E-AFM order can be explained by the symmetric exchange striction associated with the inner product of the spins (S · S).^[10] In addition, some other works on these issues are reported.^{[11– 14]}

Interestingly, the low-temperature (T) multiferroic phase in RMnO₃ is mainly determined by the magnitude of the GdFeO₃-type distortion which depends on the size of the R ion.^[15] With decreasing R-site ionic radius, four magnetic phases successively emerge at low T: the non-FE A-type antiferromagnetic (A-AFM) order, the FE ab-CS phase, the FE bc-CS phase, and the FE E-type AFM order.^[16] Thus, the substitution at the R-site with proper species becomes an efficient way to modulate the multiferroic properties in RMnO₃. Beyond TbMnO₃ and DyMnO₃, more multiferroic manganites of the CS order can be synthesized by this method such as Eu_{1 − x}Y_xMnO₃ and Gd_{1 − x}Tb_xMnO₃.^{[6, 17]} Recently, a microscopic spin model (M– F model) which includes the superexchange interaction, the single-ion anisotropy (SIA), the Dzyaloshinskii– Moriya (DM) interaction, and the spin– phonon coupling, was proposed and well reproduced measured polarization and phase diagrams of RMnO₃.^{[18, 19]} In particular, for the ab-CS phase, it was predicted that both the symmetric (S · S)-type exchange striction and antisymmetric (S× S)-type exchange striction contribute to the polarization along the a-axis, leading to a much larger total polarization P= P_AS+ P_S in the ab-CS phase than that in the bc-CS phase, where P along the c-axis is purely resulted from the antisymmetric striction, i.e., P= P_AS.^[16] Several other experimental phenomena have been qualitatively explained based on the same or similar models.^{[20– 24]}

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Crystal structure and spin-exchange interactions in orthorhombically distorted RMnO3 (ab-plane). (b) The experimentally obtained P– x data of polycrystalline Gd1 − xTmxMnO3 at T= 2  K. The polarization data are multiplied by 15 to give a reasonable estimation of P for single crystalline specimens.

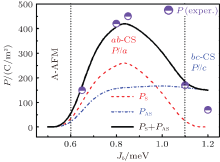
On the other hand, a quantitative calculation of the polarizations arising from the symmetric striction and antisymmetric striction respectively is essential to the complete understanding of the multiferroic properties in RMnO₃. Nevertheless, in spite of the success of the M– F model in explaining observed experiments in terms of magnetic structures and ferroelectricity, a quantitatively consistent calculation of the FE polarization has been less available.^[23] In addition, related experimental data have been rare either although Sm_{1 − x}Y_xMnO₃ was investigated in terms of P as a function of x, ^[25] since a reliable evaluation of P_AS and P_S from the measured total polarization P is a tough issue, making a quantitative and even qualitative comparison between experiments and the M– F model calculation challenging. In a recent experiment, we reported the evaluated data on P_AS and P_S associated with the ab-CS phase in Gd_{1 − x}Tb_xMnO₃ where the GdMnO₃ is located at the boundary between the A-AFM phase and ab-CS phase, and a slight substitution of Gd^{3 +} by much smaller Tm^{3 +} allows a gradual evolution of the magnetic phase from the A-AFM phase into the ab-CS phase before eventually evolving into the bc-CS phase where no component P_S is available.^[26] This allows us a specific platform at which the M– F model can be employed to calculate the P_AS and P_S in the quantitative sense. This study may provide clues to enlarge polarization and enhance the ME coupling in similar multiferroics, which is thus of particular significance.

Figure  1(b) shows the measured P at T= 2  K as a function of x in Gd_{1 − x}Tb_xMnO₃, noting here that we multiply the polarization data by 15 since our samples are polycrystalline. It was repeatedly confirmed that the P measured from single crystal samples is roughly 10– 15 times that from the polycrystalline samples, while a quantitative consistency between experiment and theory on the same order of magnitude is already satisfactory. In this work, we start from the M– F model with the Mn spin S= 2 on a cuboidal lattice and perform quantitative calculations on the polarizations of Gd_{1 − x}Tb_xMnO₃ and then compare them with measured results. The experimental results can be well reproduced, and the phase diagram at low T obtained by means of Monte Carlo simulation is discussed in detail.

The remainder of this paper is organized as follows: In Section  2 the model and the simulation method will be described. Section  3 is attributed to the simulation results and discussion. Finally, the conclusion is presented in Section  4.

The Hamiltonian can be written as H= H_ex+ H_sia+ H_DM+ H_K. The first term H_ex= ∑ _{〈 i, j〉} J_ij(S_i · S_j) denotes the spin exchange interactions, where J_a= − 0.1 and J_b are the coupling constants in the Mn– Mn bonds on the ab plane, the Peierls-type spin– phonon coupling J_ij= J_ab+ J'_abδ _{i, j} with J_ab= − 0.8 and J'_ab= 2.5 is considered for the Mn– O– Mn bonds along the x axis and the y axis (Fig.  1(a)), ^[23] δ _{i, j} denotes a further shift of the O ion between the i-th and j-th Mn ions normalized by the Mn– O bond length, and J_c= 1.2 is the strong AFM exchange in the Mn– Mn bonds along the c-axis. Here the energy unit is meV. 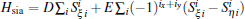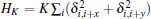The second term is the single-ion anisotropy, which consists of two parts as with D= 0.2 and E= 0.3. Here, ξ _i, η _i, ζ _i are the tilted local axes attached to the i-th MnO₆ octahedron, i_x, i_y, and i_z represent the integer coordinates of the i-th Mn ion. For their direction vectors, we use the experimental data of GdMnO₃.^[27] The third term H_DM represents the DM interactions which can be expressed by H_DM= ∑ _{〈 i, j〉} d_{i, j}(S_i× S_j). Here the DM vectors d_{i, j} are determined by five DM parameters, (α _ab, β _ab, γ _ab)= (0.10, 0.10, 0.14) and (α _c, β _c)= (0.45, 0.1). The fourth term represents the lattice elastic term, K= 400 is the elastic constant.

The values of J_a, J_ab, J_c, J'_ab, D, E, K, and five DM parameters for several RMnO₃ systems have been microscopically determined or estimated in earlier work.^[19] In addition, it is noted that the exchange path for J_b contains two O 2p orbitals, whose hybridization can be enhanced by the orthorhombic distortion. Thus, J_b can be treated as a variable which increases as the R-site ionic radius decreases. Our simulation is performed on a 36× 36× 6 cuboidal lattice with periodic boundary conditions using the standard Metropolis algorithm and temperature exchange method.^{[28, 29]} The specific heat C(T)= (〈 H²〉 − 〈 H〉 ²)/Nk_BT² and spin-helicity vector h_γ (T)= 〈 | ∑ _iS_i× S_{i + b}| 〉 /NS² (γ = a, b, c) are calculated to determine the transition points and the spin structures, here N is the number of Mn ions, k_B is the Boltzmann constant, and the brackets denote thermal and configuration averaging. It is expected that h_c (h_a) has a large value in the ab-CS (bc-CS) order, while the other two components of h are strongly suppressed. On the other hand, all these three components of h should be nearly equal to zero in the paramagnetic (PM), A-AFM and sinusoidal collinear antiferromagnetic (sc-AFM) phases. 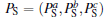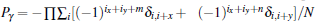In addition, based on the point charge model, the electric polarization due to the oxygen displacements δ _{i, j} induced by the symmetric exchange striction can be expressed by , where (m, n)= (0, 0) for γ = a, (m, n)= (1, 0) for γ = b, and (m, n)= (i_z+ 1, i_z+ 1) for γ = c. The constant ∏ is estimated to be 2× 10⁵  μ C/m², which is comparable with the earlier calculation.

The simulated specific heat C(T), spin helicity h_γ (T), and polarization P_S(T) due to the symmetric (S · S)-type exchange striction for a small value of J_b= 0.5  meV are presented in Fig.  2. A single phase transition can be observed in the C(T) curve, which corresponds to the transition from the PM phase into the A-AFM phase. The spin helicity vector h is nearly equal to zero constantly through this transition, and the electric polarization P_S in the A-AFM phase is extrapolated to zero at T → 0 (Fig.  2(b)). In fact, it was experimentally noted that GdMnO₃ is of the A-AFM state at low T but close to the boundary between the A-AFM order and the CS order.^{[30, 31]} Hence, the electric polarization at x= 0 observed in an earlier experiment may be due to the inhomogeneity caused by the inevitable chemical disorder and defects in realistic materials.^[32]

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Specific heat C(T), spin-helicity vector hγ (T) (γ = a, b, c), and (b) polarizations due to the symmetric (S · S)-type exchange striction PS(T) as a function of T for Jb= 0.5  meV.

The J_b is increased with increasing x. In Figs.  3(a) and 3(b), we show the calculated results for a larger value of J_b= 0.8  meV. Three successive phase transitions occur with decreasing T. The first one is the transition from the PM state to the sc-AFM state. The second one is the transition into the bc-CS order in which P_AS is induced along the c-axis. When T further falls down to the third transition point, h_c steeply increases, accompanied with the sudden drop of h_a, clearly indicating the occurrence of the transition from the bc-CS order to the ab-CS order. In addition, P^a_S equals to ∼ 250  μ C/m² at low T in the ab-CS phase (Fig.  3(b)), indicating a finite contribution of the symmetric (S · S)-type exchange striction to the ferroelectric polarization. The (S · S) contribution may be understood from the energy landscape. The ab-CS order is stabilized by the SIA and the DM interaction with vectors on the in-plane Mn– O– Mn bonds. In the absence of the DM interaction and the spin– phonon coupling, the spins rotate with the same rotation angles of ϕ _ab satisfying relation cosϕ _ab= J_ab/(2J_b). When the DM interaction is introduced, these angles are alternately modulated into ϕ _ab+ Δ ϕ _ab and ϕ _ab − Δ ϕ _ab with Δ ϕ _ab> 0 in order to get an energy gain. At the same time, the O ions between two spins with a smaller angle of ϕ _ab − Δ ϕ _ab (a larger angle of ϕ _ab+ Δ ϕ _ab) shift negatively (positively) to strengthen (weaken) the ferromagnetic exchange due to the spin– phonon coupling, leading to the generation of the macroscopic ferroelectric polarization. On the other hand, the induced polarizations between neighboring ab planes can be perfectly cancelled in the bc-CS order. As a result, there is no contribution to the ferroelectric polarization from the (S · S)-type exchange striction in the bc-CS order.

Fig.  3.

	Figure Option ViewDownloadNew Window
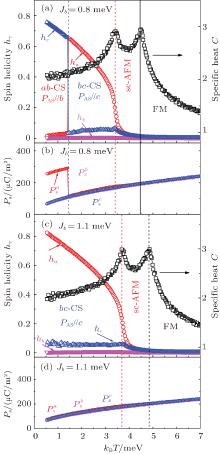	Fig.  3. C(T), hγ (T) (γ = a, b, c) as a function of T for (a) Jb= 0.8  meV and (c) Jb= 1.1  meV, and PS(T) as a function of T for (b) Jb= 0.8  meV and (d) Jb= 1.1  meV.

The third transition point shifts toward the low-T side and eventually disappears as J_b further increases, indicating the flops of the spiral-plane from the ab-plane to the bc plane. C(T) shows two peaks and h_c is small over the whole T-range for J_b= 1.1  meV (Fig.  3(c)), indicating that the ab-CS order is completely suppressed and the bc-CS order occupies the whole T-range below the second transition point. Similarly, three components of P_S in the bc-CS phase are respectively extrapolated to zero at T → 0, as clearly shown in Fig.  3(d). The ferroelectric polarization along the c-axis uniquely originated from the contribution of the antisymmetric (S× S)-type exchange striction, as reported earlier.

In order to have a quantitative comparison between our calculated polarization and the experimental results, we also calculate the (S× S) contribution at T → 0. Based on the spin-current theory, P_AS is proportional to the spin helicity h. In this work, the proportionality factor is estimated to be 200  μ C/m² due to the fact that the observed P_AS in the bc-CS order is ∼ 200  μ C/m² for Tb-doped GdMnO₃.^[17] In Fig.  4, the calculated J_b dependence of P_S, P_AS, and P_S+ P_AS at T → 0 are respectively presented. The simulated P_S+ P_AS reproduces well the experimental polarization which is also given for a clear comparison. As a result, our quantitative calculation shows good consistency with experiment results, and one may give a firm interpretation about the multiferroicity in Gd_{1 − x}Tb_xMnO₃. For small x, the ab-CS order is stabilized at low T, and remarkable polarization arises from the contributions of both the symmetric (S · S)-type exchange striction and the antisymmetric (S× S)-type exchange striction can be observed. With further Tm-substitution, the ab-CS order is replaced by the bc-CS order in which only the antisymmetric exchange striction contributes to the polarization, leading to the significant reduction of the polarization.

It is noted that the measured polarization is gradually reduced with further substitution in the experiment. This phenomenon is not reproduced in our simulation in which the polarization remains almost the same in the whole region with the bc-CS order. In fact, a similar result has been reported in an earlier simulation.^[19] The inconsistency between the theory and experiment may be due to the fact that the inevitable inhomogeneity in realistic materials is completely ignored in simulations. However, our work uncovers the multiferroic phases in Gd_{1 − x}Tb_xMnO₃, and confirms the important role of the spin– phonon coupling in the modulation of polarization in similar multiferroic materials.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Calculated Jb dependence of (S · S) contribution PS, (S× S) contribution PAS, and the summation PS+ PAS at T → 0. The summation reproduces the experimental P well.

In conclusion, we have systematically investigated the multiferroic properties in the Tm-substituted GdMnO₃ with Monte Carlo simulation of the M– F model. The experimental polarization can be well reproduced, and the phase diagram at low temperature is microscopically determined. The relatively large polarization at the low substitution level is proved to be caused by the contributions of both the symmetric (S · S)-type exchange striction and the antisymmetric (S× S)-type exchange striction in the ab-CS phase. With further substitution, a phase transition from the ab-CS order to the bc-CS order occurs, and the polarization is significantly reduced due to the fact that only the (S× S)-type exchange striction contributes to the polarization in the bc-CS order. This work is helpful for clarifying the multiferroic behaviors observed in doped manganite systems and other related multiferroic materials.