†Corresponding author. E-mail: wangrqgz@163.com
Project supported by the New Century Excellent Talents in University of China (Grant No. NCET-10-0090), the National Natural Science Foundation of China (Grant Nos. 11474106, 11174088, and 11274124), the Program for Changjiang Scholars and Innovative Research Team in University of China (Grant No. IRT1243), and the Natural Science Foundation of Guangdong Province, China (Grant No. S2012010010681).
Nonequilibrium electronic transports through a system hosting three quantum dots hybridized with superconductors are investigated. By tuning the relative positions of the dot levels, we illustrate the existence of Majorana fermions and show that the Majorana feimions will either survive separately on single dots or distribute themselves among different dots with tunable probabilities. As a result, different physical mechanisms appear, including local Andreev reflection (LAR), cross Andreev reflection (CAR), and cross resonant tunneling (CRT). The resulting characteristics may be used to reveal the unique properties of Majorana fermions. In addition, we discuss the spin-polarized transports and find a pure spin current and a spin filter effect due to the joint effect of CRT and CAR, which is important for designing spintronic devices.
Majorana fermions (MFs), with criteria of self-Hermitian and zero-energy, are predicted to be realized in condensed matter systems by combining strong spin– orbit interaction, broken time-reversal symmetry, and superconductivity.[1– 6] With their nonlocality, a pair of spatially well-separated MFs can encode a qubit, which has a great potential in fault-tolerant topological quantum computation, since the qubit encoded by MFs is robust against decoherence due to local perturbations.[7] As a consequence, searching for and controlling of the new type of particles with non-Abelian statistics are recently receiving much attention.[2– 11]
Since quasiparticles in superconductors are the superposition of electron and hole components with invariance for the exchange of the electron and hole components, superconductors provide a powerful platform to realize MFs.[12] Recently, it was predicted that Majorana bound states (MBSs) can survive at both ends of a one-dimensional (1D) semiconducting wire or the edges of a two-dimensional (2D) quantum spin Hall insulator by combining the spin– orbit coupling and the proximity effect induced by the conventional s-wave superconductor, [4, 6, 13] and the features of the topological ends or edges can be detected via electronic transport.[14– 16] By decoupling the Kitaev model[17] to a series of quantum dots (QDs) with the gate-tunable level connected by s-wave superconductors, MFs that are protected by a disorder robust topological gap can be realized at the ends of the quantum dot chain.[18, 19] For the simplest case, the system with two QDs connected by an s-wave superconductor has been investigated. It is shown that the poor man's MBSs can form on the dots under appropriate conditions, and they share all the characteristics of the standard MBSs, only lacking the topological protection.[20]
The nonlocality of MFs is usually hard to probe by electrical measurement.[21– 24] However, when they are well separated, superpositions of MF pairs can form a nonlocal fermion level. As a result, the cross correlation is introduced to certify the nonlocality of MFs. It is addressed that the nonlocality of a pair of MBSs can be probed in conductance as well as noise cross correlation for cross Andreev reflection (CAR).[25, 26] Among these, the use of quantum dots to probe MFs is widely studied.[10, 18, 19, 25– 34] For instance, two QDs are inserted between a nanowire's ends hosting MFs and metal leads to suppress the effect from the local Andreev reflection (LAR).[27, 28] For the case of weak dot– reservoir coupling, it is found that the cross correlation can be both negative and positive, depending on the quantum dots' relative levels.[27] For strong dot– reservoir coupling, the cross correlation exhibits a clover-like shape, [28] and vanishes when one of the dot levels is in resonance with the Majorana zero mode.[26]
In this paper, we study a system consisting of three QDs connected to two conventional superconductors. By tuning the relative position of the dot levels, we demonstrate the existence of MFs and show that the MFs either survive on a single dot separately or extend themselves among different dots with tunable probabilities. As a result, there are different physical mechanisms, including the LAR, CAR, and cross resonant tunneling (CRT). These mechanisms are modulated by MBSs and can be switched to each other by tuning the system parameters, which characterizes the unique properties of MFs. In addition, spin-polarized transports are discussed, and a pure spin current and the spin filter effect are presented as a result of the combination of CRT and CAR.
The paper is organized as follows: in Section 2, we establish a theoretical model and search for the realization of MBSs. The different mechanism governed average currents, shot noise, and spin-dependent transports are discussed in Section 3. In the last section, a short summary is given.
We consider a system of three coupling QDs connected to two conventional superconductors, as schematically shown in Fig. 1. The coherent lengths of the superconductors are assumed to be larger than their geometric lengths so as to allow the CAR related to electrons on different dots. The superconductors are grounded, and the two ends of the system (dot 1 and dot 2) are respectively connected to, via tunnel coupling, two normal metal leads with chemical potential μ L(R) (not shown in Fig. 1).
The Hamiltonian of the system under investigation is written as H = Hlead+ Hcent+ Hlead-cent, including the Hamiltonian of the normal metal reservoirs with dispersion spectrum ɛ α , k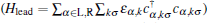

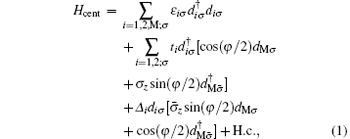
where σ z, 
Firstly, we assume the Zeeman splitting to be larger than the temperature, for which only one spin level, e.g., σ = ↓ , is within the window of transport. In this case, Hamiltonian (1) is reduced to a spinless model as in Ref. [20]
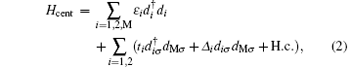
where for simplicity the dependence on φ has been absorbed into ti and Δ i, which is reflected by the tunable ratio Δ i/ti.
In a Nambu presentation, Hamiltonian (2) can be expressed as
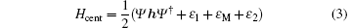
under the basis Ψ = (d1† , dM† , d2† , d1, dM, d2) with

where we have assumed the superconductors have the same phase and so choose Δ i and ti to be real for simplicity. We diagonalize the Hamiltonian h and solve the corresponding Bogoliubov– de Gennes equation[18, 26]
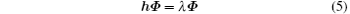
with ϕ = (ϕ 1, ϕ 2, ϕ 3, ϕ 4, ϕ 5, ϕ 6) to search for zero-energy quasiparticles of Majorana states. Then the quasiparticle operators can be expressed as γ i = ϕ i· ψ † .
When the levels of dot 1 and dot 2 are aligned with the chemical potential of the superconductors (μ S = 0), namely, ɛ 1 = ɛ 2 = 0, we can always find two zero-energy solutions to Eq. (5) for ti = Δ i, reading

They clearly obey the Majorana criterion γ † 1(2) = γ 1(2), and therefore describe MBSs. Interestingly, one can notice that the two Majorana states are well spatially separated since γ 1 and γ 2 are completely localized on dot 1 and dot 2, respectively. Furthermore, these states are independent of the middle dot level ɛ M. If we loosen the constraint and only set ɛ 2 = 0, there are still two zero-energy states, which can be reduced to
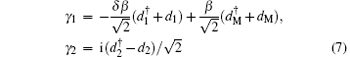
for ɛ M = 0, where we denote δ = 2Δ 1/ɛ 1 and 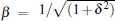

To compute the transport properties, we switch to the many-particle presentation on the basis |n1nMn2〉 , where n1, M, 2 = 0 or 1 represents the occupation of the QDs. Without lead– dot couplings, the parity of the central region is conserved though the particles are not invariant, since the electrons are absorbed into or split out from the superconductors in pairs. Therefore, the Hamiltonian of the central region Hcent is block diagonal in the Hilbert space spanned by the parity subspace, namely,

Here He for even parity subspace
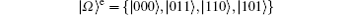
and Ho for odd parity subspace

are given by
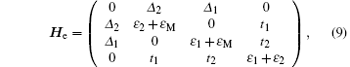

The diagonalized master equation approach extending the infinite-bias limit to an arbitrary bias voltage[27, 29, 30, 36, 37] is adopted. Firstly, by diagonalizing the Hamiltonian He (Ho), we obtain the eigenvectors |ei〉 (|oj〉 ), i.e.,
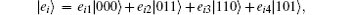
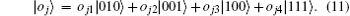
The lead– dot Hamiltonian Hlead-cent mixes the states of different blocks via breaking the parity conservation and contributes to the current by tunneling the matrix elements

with 〈 ei|di|ej〉 = 0 and 〈 oi|di|oj〉 = 0. We consider the case of weak lead– dot coupling, Γ α ≤ kBTα , ti, so that the current and the shot noise properties of the system are determined by the reduced density matrix ρ cent, ρ cent = ∑ lPl|l〉 〈 l| (|l〉 ∈ {|ei〉 }, |oj〉 }) with Pl the probability of finding the central state at |l〉 . Then, we gather all the probabilities as a column vector P, thus, the matrix form of the rate equations can be written as
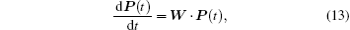
with the matrix elements
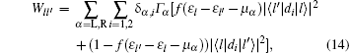
and Wll = – ∑ l′ ≠ lWl′ l. Here, δ α , i = 1 for α = L (or R) and i = 1 (or 2), and δ α , i = 0 otherwise, ɛ i(e) (ɛ j(o)) is the eigenvalue corresponding to eigenvector 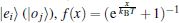

where the summation goes over all vector elements k. The Î α is the matrix form of the current operator, whose matrix elements have similar expressions as Wll′ in Eq. (14), only replacing the positive sign + with negative sign – and taking α = L or R.
With the combination-generation approach, [38– 40] the noise correlators are given by
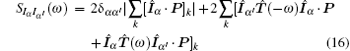
with 
With numerical calculations, we discuss the case of symmetrical tunnel coupling Γ L = Γ R = Γ 0≤ kBT0 (in experiments, the lead– dot coupling energy is Γ 0∼ 0.01 meV[41, 42]), where TL = TR = T0, and we set Δ 1 = Δ 2 = Δ 0 and t1 = t2 = t0 for the sake of simplicity.
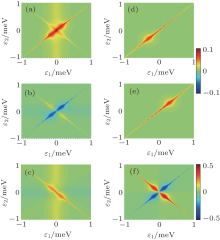
The calculated current Iα through the α lead and the net current Inet = IL+ IR through the superconductors are plotted as a function of dot levels ɛ 1 and ɛ 2 in Fig. 2. Figures 2(a) and 2(b) indicate that IL(R) exhibits maximal absolute values around ɛ 1(2) = 0. It is attributed to the LAR process with a pair of electrons absorbed by or emitted from the same lead. For the original point ɛ 1 = ɛ 2 = 0, from Eq. (6), we know that two uncoupled MBSs are located respectively on dot 1 and dot 2, and so IL and IR reach the maximal values regardless of ɛ M. In the limit of μ L = – μ R→ ∞ , the current solution can be analytically expressed as |IL(R)| = Γ L(R)/2. LAR's local feature is also manifested by zero-frequency cross current correlation SLR(0) = 0 (see Fig. 2(f)). When we keep ɛ M = 0 and let either dot level align with the superconductor one, e.g., ɛ 2 = 0, as shown in Fig. 3(a), the variation of ɛ 1 away from zero does not influence IR, but reduces IL from a peak to zero quickly. This can be understood based on Eq. (7), i.e., tuning of ɛ 1 transfers the weight of the Majorana wave function γ 1 from dot 1 to the middle dot, but is irrelevant to MBS γ 2 on dot 2. For finite ɛ M and ɛ 2 = 0, IR exhibits a similar scenario of current peak as in IL out of the same reason, namely, the weight of γ 2 distributes between dot 2 and dot M at ɛ M≠ 0. For the general case of finite ɛ M and ɛ 2, as depicted in Figs. 3(b)– 3(d), the LAR current peak is sensitive to ɛ M and vanishes for ɛ M> 0.25 meV.
In Figs. 2(a) and 2(b), apart from the LAR current peaks along the axis, one can simultaneously notice that there emerge two types of subpeaks: a negative one (electron tunnels out of the central region to the leads) along the diagonal region (ɛ 1 = ɛ 2) and a positive value (electron tunnels into the central region from the leads) along the anti-diagonal region (ɛ 1 = – ɛ 2). What is more, for the former, IL has the same value as IR but with an opposite sign, obeying IL = – IR, thus Inet = 0 holds exactly. While for the latter case, IL = IR holds strictly. These relations can also be seen in Figs. 3(b)– 3(d). In fact, different physical mechanisms exist. Physically, IL = IR implies a CAR process, while IL = – IR is for electron tunneling from the left lead to the right lead. To distinguish them, we further plot the dependence of IL on ɛ 1 and ɛ 2 for t0 = 0 (Fig. 2(d)) and Δ 0 = 0 (Fig. 2(e)), where the anti-diagonal peak vanishes and only the diagonal peak remains. For t0 = 0, an electron tunnels from dot 1 to dot 2 through absorbing and splitting Cooper pairs simultaneously, while for Δ 0 = 0, an electron tunnels via the middle dot normally. These two cases cannot form the CAR process but with a resonant tunneling feature, so we name them as cross resonant tunneling (CRT). For the former, the arrangement of ɛ 1 = ɛ 2 = – ɛ M is in favor of the formation of zero-energy Cooper pairs between dot 1 (or dot 2) and the middle dot, thus there appears a current resonance region around ɛ 1 = ɛ 2 = – ɛ M, see Fig. 2(d). For the latter, the identical level of ɛ 1 = ɛ 2 = ɛ M favors the resonant tunneling through the middle dot, so exhibiting a current resonance here, see Fig. 2(e). In contrast, for the arrangement of ɛ 1 = – ɛ 2, a pair of electrons from two dots have zero total energy and so can form a Cooper pair entering into the superconductor together. As a result, IL and IR have the same value and sign.
In Fig. 2(f), the zero-frequency current noise cross correlation SLR(0) is displayed in the ɛ 1– ɛ 2 plane. Interestingly, different physical processes are characterized. The CAR process involved in the electron pair movement is a positive correlation, while the CRT tends to tunnel into one dot and out of the other. The opposite tunnelings generate negative correlations. Therefore, in a whole, SLR(0) exhibits a quadrupole pattern with alternating positive and negative values. This pattern is robust against the bias setting applied to the normal leads.
Interestingly, the bias setting has a great influence on the currents. In Fig. 3(c), we illustrate the variation of the currents for different chemical potentials of the right lead (μ R) by fixing μ L at 0.2 mV. By tuning μ R, the weight of the current peaks of CAR and CRT, respectively located at ɛ 1 = – ɛ 2 and ɛ 1 = ɛ 2, can be redistributed between them. For μ R = – μ L, the CAR current peak is completely suppressed (see the short-dot lines in Fig. 3(c)) due to the opposite movement of electrons in different leads. As we increase μ R from μ R = – μ L, the CAR current peak increases gradually, while the CRT current peak is reduced correspondingly (see the solid lines in Fig. 3(c)) and eventually vanishes at μ R = μ L, which favorably provides the electrons with the same direction and so favors the CAR process (see the dash-dot lines in Fig. 3(c)). Therefore, mediating μ R can be applied to observe the transition between the CRT and CAR mechanisms. In addition, we plot the dependences of the currents on ɛ M and t0 respectively in Figs. 3(b) and 3(d), where the increase in ɛ M and t0 is only to widen the resonant peaks, irrelevant to the peak height. Our numerical calculations also show that with the increase in temperature, the LAR current peaks will decrease, while the CAR and CRT current peaks will increase to maximum values before reducing.
From the above analysis, we know that there are two different physical mechanisms contributing to the current in the right lead with opposite flowing directions. This makes one recall the generation of a pure spin current where two spin species transfer with the same magnitude but opposite directions. In order to generate a pure spin current, we set the spin-degenerated dot levels ɛ 1σ = ɛ 1 and ɛ Mσ = ɛ M, while the spin levels ɛ 2↑ (↓ ) = ɛ 2∓ Δ B/2 on the right dot are lifted by Zeeman energy Δ B which is tuned to be comparable with other parameters. Consequently, both spin species take part in the transport, as depicted schematically in Fig. 4. For the right lead, if setting ɛ 2 = 0 and ɛ 1 align with ɛ 2↓ , spin-down electrons tunnel from the left lead to the right lead via the CRT mechanism, contributing the forward spin-down current. At the same time, ɛ 1 = – ɛ 2↑ is also satisfied and so the CAR mechanism generates the backward spin-up current. Thus a pure spin current emerges in the right lead when IR↑ = – IR↓ .
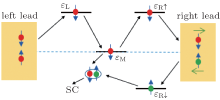 | Fig. 4. Schematic diagram of generation of a pure spin current when both spin levels contribute to the transport. |
The above arguments are confirmed by the following numerical results. We start with the full spin Hamiltonian in Eq. (1), whose block diagonal matrices in Eq. (8), under the basis |n1σ n2σ nσ M〉 with nσ 1, 2, M = 0, ↑ , ↓ , are 13× 13 He and 14× 14 Ho. We still employ the rate equation (13) to obtain the occupied probability for eigenstate |l〉 of Hcent with the transition matrix elements
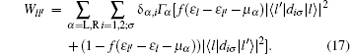
The spin-dependent current Iα ↑ (↓ ) is calculated by

where the current matrix Î α σ is spin dependent with matrix elements
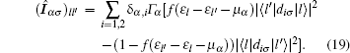
One can notice that the spin-dependent current stems from the spin-selection rule 〈 l|diσ |l′ 〉 , namely,
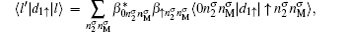
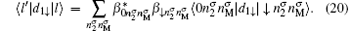
Here, 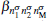
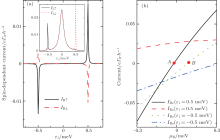
In Fig. 5, we display the spin-dependent currents IR↑ and IR↓ as a function of ɛ 1. Obviously, at ɛ 1 = ɛ 2↓ = 0.5 meV, a large spin current IRs and a small charge current IRc appear due to the opposite signs for IR↑ and IR↓ . If one chooses appropriate μ R, as shown in Fig. 5(b), a pure spin current can be realized at certain μ R, where IRc = 0 and IRs ≠ 0 (see point A in Fig. 5(b)). Similarly, at ɛ 1 = – ɛ 2↑ = 0.5 meV, a pure spin current is also obtained but with a different direction (see point B in Fig. 5(b)). At the same time, one can notice that when a pure spin current is realized in the right lead, the spin filter effect (existence of the current of only one spin component and the other vanishing) is present in the left lead, which is indicated in the inset of Fig. 5(a).
Epitaxially grown InSb quantum dots may be suitable materials to form the excitation of Majorana fermions, since InSb possesses a large electron g factor (|g* |∼ 30– 70) and a strong spin– orbit interaction (with energy Δ SOI∼ 0.3 meV).[43] Therefore, for possible experimental demonstration, the system could be built by placing InSb quantum dots on an s-wave superconductor substrate (with superconducting gap Δ ∼ 0.2 meV) under an external applied magnetic field of a moderate strength (0.15 T). The diameter of the quantum dot is about 200 nm, while the coherent length of a superconductor is approximately 216 nm, electrons therefore can tunnel between neighboring dots either through normal tunneling with coupling strength t1(2) or CAR with pairing potential Δ 1(2) induced by the superconductor. Nevertheless, the two outmost dots are disconnected with each other because the distance between them is beyond the superconductor's coherent length. Under these conditions, the model proposed in our paper can be realized. The energy level of the quantum dots, in reality, can be modulated by gate voltages, and the tunneling rates Γ L(R) and coupling strength tL(R) can also be controlled by utilizing the gate-voltage technique. As for the chemical potential μ L(R), we can tune them independently when two power sources are applied, respectively, between lead L coupling to dot 1 (or lead R coupling to dot 2) and the superconductor.
We study the transport properties through a setup with three QDs hybridized with conventional s-wave superconductors. By tuning the dot levels, we present the realization of MFs and show that the MFs either locate on different dots separately, or distribute themselves among different dots with tunable possibilities, depending on the relative positions of the dot levels. As a consequence, the nonequilibrium electronic transports show rich physical mechanisms, including the LAR, CAR, and CRT. These mechanisms are modulated by the Majorana states and can be switched to each other by tuning the system parameters, which reveals the unique properties of Majorana fermions. In addition, spin-polarized transports are discussed. Interestingly, we find a pure spin current and a spin filter effect originating from the joint effect of CRT and CAR. We expect that our findings will be helpful for experimentally detecting MFs and designing spintronic devices.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|