†Corresponding author. E-mail: lyhndl@163.com
Previous experimental investigations have shown that when a narrow pipe is inserted into a granular bed and is vibrated vertically but the granular bed is kept still, the grains in the bed can enter the pipe and rise against gravity along the pipe and finally stabilized at a certain height. The growth velocity and final stable height of the grain column inside the pipe can be controlled by varying the vibration conditions. In this paper, we discuss those experimental findings. We establish a mathematic relation between the grain column height ( h) and time ( t), and by using the relation we discuss the change of the growth velocity (d h/d t) and acceleration (d2 h/d t2) with t and h, respectively. We also analyze the mechanism of the rising motion of the grains during vibration. Furthermore, we derive a theoretical expression for describing the final stable height ( hst), which shows that the main factors influencing the height are vibration strength ( Γ ), bulk density of grains, inner diameter of the pipe, and vibration frequency, and that hst increases nonlinearly in the presence of air and linearly in a vacuum environment with increasing Γ.
Granular materials, when subjected to external excitation, exhibit many interesting behaviors that are different from those of liquids or solids.[1, 2] For example, under vertical vibration, granular materials exhibit behaviors such as convection, [3] surface waves, [4] size separation, [5, 6] grain migration in a U-shaped tube, [7] oscillons on the free surface, [8] soliton-shape heaping, [9] and so on.
Akiyama et al.[10, 11] found that if a tube is inserted into a particle bed and is held stationary, when the bed vibrates vertically, the surface level of the bed within the tube rose or fell and stabilized at a level different from that of the bed outside the tube. As a result, a height difference is held between the inside and outside of the tube. Maeno[12] discussed the factors influencing the height difference by using numerical model. With the help of the discrete element method, Tatemoto et al.[13] concluded that the ratio of the cross section inside the tube to that at the annulus strongly affects the height difference. In Ref. [14], Chen et al. vertically inserted a glass tube into a granular layer (which is fixed on the bed body and vibrates with the bed synchronously) and filled the tube with grains to a certain height before the bed vibrates. They found that if the grain column in the tube is above (or below) the ambient height, then it will go up (or down) when the bed starts vibrating vertically. They called this case a “ capillarity-like phenomenon” . Liu et al.[15] used a cylinder (filled with glass beads) as a granular bed and placed a container (a beaker or test tube) upside down on the surface of the granular layer. They found that while the bed vibrates, the pressure at the top of the container fluctuates above and below the atmospheric pressure, and a reciprocating air flow existing between the tube and the bed brings the glass beads’ directional upwards movements. All of these investigations[10– 15] have shown that when a granular bed vibrates vertically, the grains can rise against gravity along the pipe.
More recently, Zhang et al.[16] and Liu et al.[17] designed a new experimental method for studying the rising motion of grains in a narrow pipe. They inserted the pipe in the center of a granular bed and vertically vibrated the pipe but kept the granular bed still. They found that at a sufficiently large vibration strength, the grains (glass beads) can rise against gravity along the pipe and finally stabilized at a certain height. The growth velocity and final stable height of the grain column inside the pipe can be controlled by varying the vibration strength. Their experimental method can probably be used to develop some new approaches to hoisting and transporting of granular material and is worthy of further study. More important, this experimental method is different from those in which the granular bed is vibrated but the pipe is kept still. Therefore, the new phenomena and results shown in the experiments need to be carefully analyzed and discussed.
The objective of this paper is to try to describe and analyze these new experimental results and to discuss the main factors influencing the results and to explain some experimental phenomena.
The organization of this paper is as follows. In Section 2 we briefly summarize the experimental findings by Zhang et al.[16] We establish a semi-theoretical mathematical relation between the grain column height (h) and time (t), and further discuss the change of the growth velocity (dh/dt) and acceleration (d2h/dt2) with t and h, respectively in Section 3. In Section 4, we propose a new mechanism of the rising motion of the grains inside the pipe during vibration, which is different from those proposed in Refs. [16] and [17]. In Section 5, we discuss the condition under which the grain column reaches the final stable height and derive a theoretical expression for describing the stable height, and analyze the main factors influencing the height. Our conclusions are given in Section 6.
The experimental setup is a cylinder with inner diameter of 200 mm, filled with glass beads with an average diameter of 0.3 mm and real density of 2.5 g/cm3, respectively. The height of the granular bed consisting of glass beads is 200 mm and the bulk density is 1.542 g/cm3. A transparent plexiglass pipe, with an inner diameter of 8 mm, length of 800 mm, and wall thickness of 1.5 mm, is inserted vertically into the granular bed, and the insertion depth of the lower end of the pipe is 35 mm. The pipe is mounted on the vibrating table of an electromagnetic exciter that is driven sinusoidally. The main control parameters for vibration are vibration frequency (f) and dimensionless vibration strength Γ = A (2π f)2 /g, where A is the vibration amplitude, and g is the gravity acceleration (g = 9.81 m/s2). The pipe is vertically vibrated at a fixed frequency of 12 Hz, but with different vibration strengths. A high-speed camera is used to observe the height of grain column inside the pipe during vibration and the upper surface of the granular bed is taken as the zero of the grain column height. Because the inner diameter of the pipe is much smaller than that of the cylinder, the change in the granular bed height inside the cylinder can be neglected when the beads rise and fill the pipe.
Our experimental results showed that if the initial height of the grain column (h0) is equal to zero, when the vibration strength Γ is larger than a threshold value, then the grains in the bed can enter the pipe and rise against gravity along the pipe and finally stabilized at a certain height. Figure 1 shows the change in the height (h) of the grain column inside the pipe with time (t), where the squares and diamonds represent experimental data at Γ = 3.3 and Γ = 5.0, respectively. It can be seen that the grain column height increases with increasing t once the pipe vibrates and finally reaches a stable level (hst) and keeps unchanged. The growth velocity of the height increases at first, but when the height grows to a certain level, the growth velocity slows down gradually. The larger the vibration strength Γ , the faster the growth of the height, and the larger the final stable height of the grain column.
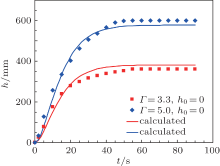 | Fig. 1. Change in the height (h) of the grain column inside the pipe with time (t) at Γ = 3.3 and Γ = 5.0, respectively. h0 is the initial height of the grain column. The solid lines are the calculating values using Eq. (6). |
Experiments were also conducted under the condition that the pipe is filled with grains to an initial height of h0 (h0 > 0) before vibration and the results indicated that in case of h0 > hst, the grain column height will continuously decrease until h = hst; in the case of h0 < hst, the grain column height will continuously increase until h = hst. For example, when Γ = 3.3, hst is 360 mm. By taking h0 = 500 mm (h0 > hst), the height continuously decreases and finally stabilizes at hst = 360 mm, as shown in Fig. 2(a). When Γ = 5.0, hst is 600 mm. By taking h0 = 500 mm (h0 < hst), the height continuously increases and finally stabilizes at hst = 600 mm (see Fig. 2(b)).
Figure 3 shows the experimental results of the final stable height (hst) versus vibration strength (Γ ). The squares and diamonds represent the experimental values in the presence of air and in a vacuum environment, respectively. Figure 3 indicates that hst in the presence of air is larger than that in a vacuum environment and increases nonlinearly with increasing Γ . However, in a vacuum environment, there is a nearly linear relationship between hst and Γ .
 | Fig. 3. Final stable height (hst) versus the vibration strength (Γ ). The squares and diamonds represent the experimental values in the presence of air and in a vacuum environment, respectively. (a) The dotted and solid lines are calculating results using Eqs. (11) and (12), respectively, where ρ v = 1.542 × 10− 3 g/mm3, d = 8 mm, f = 12 Hz, k0 = 2.061 × 106, k1 = 5.38 × 104, Γ 0 = 1.024; (b) experimental data are cited from Ref. [17]. The dotted and solid lines are the calculating results using Eqs. (11) and (12), respectively, where ρ v = 1.542 × 10− 3 g/mm3, d = 8 mm, f = 12 Hz, k0 = 3.694 × 106, k1 = 8.57 × 105, and Γ 0 = 1.181. |
According to the experimental results in Fig. 1, the grain column height increases with increasing t and finally reaches a stable level. The growth velocity of the height (dh/dt) increases at first and then slows down gradually. This implies that there is a peak at the curve of dh/dt versus t. Therefore, we can suppose that dh/dt is proportional to t · e− at. Moreover, a larger vibration strength (Γ ), i.e., a larger vibration amplitude A (A = Γ g/(2π f)2) can cause a larger growth velocity. Hence, dh/dt is proportional to A. From the above results we obtain
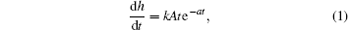
where k is a proportional coefficient, and a is a parameter to be determined later.
Integrating Eq. (1) yields

where c is an integration constant. According to the initial condition of h = 0 at t = 0, we obtain

Substituting Eq. (3) into Eq. (2) yields

Substituting A = Γ g/(2π f)2 into Eq. (4), we can rewrite it as

Formula (5) indicates that when f is fixed, both a larger Γ and a longer t can cause a larger h, and if t is long enough, h → ka− 2Γ g/(2π f)2, i.e., the height of the grain column reaches a stable level.
By taking a = 0.135 and k = 1.222 (which are determined by data fitting) in Eq. (5), we obtain a relation between h and t as follows:
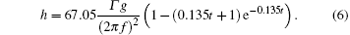
The solid lines in Fig. 1 are the calculating values by Eq. (6), which are basically consistent with the experimental data points.
Using Eq. (6) we calculate the change in the growth velocity of the height v (dh/dt) and acceleration a (d2h/dt2) with t and h, respectively, the results are shown in Fig. 4. It can be seen from Fig. 4 that initially the growth velocity of the height speeds up (a > 0), but the acceleration decreases gradually with increasing t and h. When the height grows to a certain level (a = 0), the growth velocity begins to fall (a < 0) and trends to zero gradually.
The authors in Ref. [17] proposed a mechanism of the grains’ rising motion. They concluded that the particles are lifted by the tube during its upward movement. During this period, a void may be formed at the tube bottom that is quickly filled by the particles in the silo. When the particles fall, the filled particles place an upward force on the particles in the tube. At the end of the downward movement, the particles in the tube cannot return to their initial positions at the beginning of the upward movement, resulting in “ particle climbing” .
In Ref. [16], the mechanism proposed by authors is different from that in Ref. [17]. They think that during the upward movement of the pipe, the grains in the pipe are lifted by the pipe. When the pipe moves downwards, the fall of the grains in the pipe lags that of the pipe itself. At the end of the downward movement, the grains cannot return to their initial positions at the beginning of the upward movement. As a result, a void is formed at the lower part of the pipe. This void is filled by grains in the granular bed and the grains in the pipe cannot return to their initial positions, resulting in “ grain filling against gravity” .
The authors of Refs. [16] and [17] all thought that a void will be formed, but there is a difference between them in when and where the void is formed. The former thinks that the void is formed during upward movement of the pipe, whereas the latter thinks that it is formed at the end of the downward movement. When and how the grains in granular bed enter the pipe is not expounded. In addition, the experimental phenomena shown in Fig. 2(a), in which the grain column height continuously decreases, cannot be explained by the mechanisms.
In the following, we try to analyze the mechanism in detail. We suppose that when the pipe starts vibrating it moves upwards firstly and then downwards, with an initial grain column height of h0 = 10 mm.
Let us consider the first vibration cycle. When the pipe moves upwards, the grains in the pipe also move upwards with the pipe due to the friction force of pipe wall. Furthermore, as the pipe moves upwards, a void will be formed under the lower end of the pipe and is filled at once by grains in the granular bed. When the pipe turns to move downwards, the grains in the bed possess an upward “ relative velocity” relative to the moving pipe and immediately “ move upwards” to enter the pipe at this velocity. These newly-entering grains collide with the already-existing grains, generating a driving force to the latter. If the relative velocity of the newly-entering grains is large enough (their kinetic energy is larger than the gravitational potential energy of the already-existing grain column), the collision can change the motion state of the already-existing grains and force them to move upwards for a certain distance. The newly-entering grains occupy the positions where some of the already-existing grains were, therefore, the already-existing grains cannot return to their initial positions. The newly-entering grains plus the already-existing grains result in a growth of the grain column height.
From the second cycle on, the movement of the grains in each cycle will repeat that in the first cycle. As the number of cycles increases, the grain column height increases step by step. When the grain column height is high enough and the potential energy of the grain column balances with the kinetic energy of the newly-entering grains, the height stops growing and stabilizes at a certain level.
The above description of mechanism can help us to understand when and how the grains in the bed enter the pipe and how the height of grain column grows step by step, and finally reaches a stable level.
The kinetic energy of the newly-entering grains is dependent on the kinetic energy of the vibration, i.e., the vibration strength Γ , and a smaller Γ generates a smaller kinetic energy. If the kinetic energy of the grains in the bed is smaller than the gravitational potential energy of the grain column (for example, a very high initial height or a smaller Γ ), when the pipe moves downwards, the collision between grains in the bed and grain column cannot change the motion state of the latter, and the latter prevents the former entering the pipe. When the pipe turns to move upwards, a part of grains near the lower end of the pipe will fall back to the bed, resulting in a decrease in both the height and the potential energy of the grain column.
According to above mechanism, the experimental phenomena shown in Fig. 2 can be explained as follows.
As shown in Fig. 2(a), the pipe is filled with grains to an initial height of h0 = 500 mm, larger than hst (360 mm) at Γ = 3.3, which means that the kinetic energy of the grains in the bed is smaller than the potential energy of the grain column (due to a smaller Γ ). Therefore, when the pipe moves downwards, the grain column prevents grains in the bed entering the pipe. When the pipe turns to move upwards, a part of grains in the pipe fall back to the bed, which causes a decrease in the grain column height. As the pipe vibrates continuously, the height decreases continuously. After many vibration cycles, when the potential energy of the grain column balances with the kinetic energy, the height stops falling and stabilizes at hst.
As for Fig. 2(b), although h0 is as high as 500 mm, it is lower than hst (600 mm) at Γ = 5.0, which means that the kinetic energy of the vibration is larger than the potential energy of the grain column (due to a larger Γ ). When the pipe moves downwards, the grains in the bed can still enter the pipe, both the height and the potential energy of the grain column can increase. After many vibration cycles, when the potential energy balances with the kinetic energy, the height stops rising and stabilizes at hst.
In this section, we discuss the condition under which the grain column height reaches a stable level (hst).
As discussed before, because the granular bed is still, the grains in the bed do not possess velocity and kinetic energy. When the pipe moves downwards, the grains in the bed possess an upward “ relative velocity” relative to the moving pipe and can enter the pipe at this velocity. The newly-entering grains collide with the existing grain column and force the latter to move upwards for a distance, which means that the kinetic energy of the former is transferred to the latter by the collision and the gravitational potential energy of the latter increase. Only when the kinetic energy of the former is larger than the potential energy of the latter, can the potential energy of the latter increases. After the grain column height reaches hst, few grains can enter the pipe. In such a case, when the pipe vibrates, the grains in the bed collide with the grains which are inside and near the lower end of the pipe, and the kinetic energy of the vibration is transferred to the grain column and helps it to keep the height and the potential energy unchanged. Therefore, the condition under which the grain column height reaches hst should be that the potential energy of the grain column is equal to the kinetic energy of the vibration.
We take the lower end of the pipe as the zero of gravitational potential energy. Therefore, the potential energy of the grain column, EP, can be expressed as EP = mg(hst + hin)/2, where hin is the insertion depth of the lower end of the pipe, (hst + hin)/2 is the height of the mass center of the granular column relative to the zero of potential energy, m is the mass of the grain column, which can be calculated by m = ρ vπ (d/2)2 (hst + hin), where ρ v is the bulk density of the grain column and d is the inner diameter of the pipe. When hst is much larger than hin, we take hst ≈ hin+ hst, and EP can be expressed as

Because the vibration of the pipe is a simple harmonic vibration, the mean value of the kinetic energy of the vibration, Ē k, is equal to half of the total energy (E), i.e., Ē k = E/2, and the total energy is proportional to the square of the vibration amplitude: E ∝ A2. For convenience of discussion, we express the kinetic energy of the vibration as Ē k = k0A2, where k0 is a proportional coefficient.
In addition to the potential energy and kinetic energy, the effect of air should also be taken into consideration. As shown in Fig. 3, hst in the presence of air is larger than that in a vacuum environment. In the presence of air, when the pipe moves downwards, the interstitial air among grains enter the pipe together with the grains at the same velocity as the grains. The kinetic energy of the moving air can generate an upward additional force to the grains inside the pipe. The kinetic energy of the moving air can be expressed as[18]

where ρ a is the mass density of air, S is the section area of air flow, and ν is the velocity of air motion. Because the vibration velocity of the pipe ν is proportional to A (ν = − ω Acos ω t), the velocity of the air motion is also proportional to A, i.e., ν ∝ A. Hence, we take Eair = k1A3, where k1 is a proportional coefficient.
Based on the discussion above, when the grain column height reaches hst, the following equation should be satisfied:
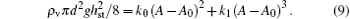
The left side of the equation is the potential energy of the grain column and the right side represents the kinetic energy of the vibration and the kinetic energy of the moving air. A0 is the minimum vibration amplitude beyond which the grains can rise against gravity.
Substituting A = Γ g/(2π f)2 and A0 = Γ 0g/(2π f)2 into Eq. (9) yields
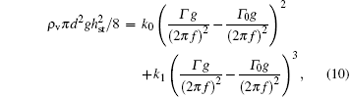
where Γ 0 is the minimum vibration strength beyond which the grains can rise against gravity.
From Eq. (10) we can obtain

Under vacuum, formula (11) can be simplified into

Formulas (11) and (12) indicate that hst in the presence of air is larger than that under vacuum and increases with increasing Γ nonlinearly in the presence of air and linearly under vacuum. Figure 3 shows that the calculation results obtained by Eqs. (11) and (12) are qualitatively consistent with the experimental data points.
Formula (11) also shows that the main factors influencing hst are vibration strength Γ , bulk density of the grain column ρ v, inner diameter of the pipe d, and vibration frequency f, which involve the physical properties of the grains, the size of the pipe and vibration conditions. hst increases with increasing Γ but decreases with increasing ρ v, d, and f. The experimental results in Ref. [16] show that particle climbing is weakened with increasing pipe diameter and even disappears when the pipe diameter is too large. Equation (11) indicates that the larger the pipe diameter d, the smaller the stable height hst, which is consistent with the above result.
From formula (11) we can also obtain some other inferences. For instance, when hst is fixed, the increase in d can increase the transport capacity of the grains, but only when Γ is increased synchronously, can hst keep unchanged.
By vibrating a pipe vertically and keeping the granular bed still, the grains in the bed can enter the pipe and rise against gravity along the pipe. The growth velocity and the final stable height of the grain column inside the pipe can be controlled by changing the vibration conditions. This method can be probably used to develop some new approaches to the hoisting and transporting of granular material and is worthy of further study and improvement.
Formula (6) proposed in this paper can quantitatively describe the evolution of the grain column height with time. The mechanism of the rising motion of the grains is expounded as follows: when the pipe moves upwards, the grains in the pipe also move upwards with the pipe due to the friction force of pipe wall. When the pipe turns to move downwards, the grains in the bed possess an upward “ relative velocity” relative to the moving pipe and move upwards to enter the pipe. These newly-entering grains collide with the already-existing grains, generating a driving force to the latter. If the relative velocity of the newly-entering grains is large enough (their kinetic energy is larger than the gravitational potential energy of the already-existing grain column) the collision can force the existing grains to move upwards for a distance. The newly-entering grains plus the existing grains result in a growth of the grain column height. The condition under which the grain column height reaches hst is that the gravitational potential energy of the grain column is equal to the sum of the kinetic energy of the vibration and that of the moving air. The main factors influencing hst are vibration strength, bulk density of grains, inner diameter of pipe, and vibration frequency. hst increases with increasing Γ nonlinearly in the presence of air and linearly under vacuum. The research in this paper can serve as a base for future studies.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|




