†Corresponding author. E-mail: qinglai.wei@ia.ac.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61034002, 61233001, 61273140, 61304086, and 61374105) and the Beijing Natural Science Foundation, China (Grant No. 4132078).
A policy iteration algorithm of adaptive dynamic programming (ADP) is developed to solve the optimal tracking control for a class of discrete-time chaotic systems. By system transformations, the optimal tracking problem is transformed into an optimal regulation one. The policy iteration algorithm for discrete-time chaotic systems is first described. Then, the convergence and admissibility properties of the developed policy iteration algorithm are presented, which show that the transformed chaotic system can be stabilized under an arbitrary iterative control law and the iterative performance index function simultaneously converges to the optimum. By implementing the policy iteration algorithm via neural networks, the developed optimal tracking control scheme for chaotic systems is verified by a simulation.
The control of chaotic systems has been the focus of control research in the past decade.[1– 7] For most control methods of chaotic systems, such as impulsive control methods[2– 4, 6] and adaptive synchronization control methods, [8– 10] only the stability properties of the chaotic systems are considered. The optimality property is an important performance of chaotic control systems. As is well known, dynamic programming is a very useful tool in solving optimal control problems.[11] However, due to the difficulties related to solving the time-varying Hamilton– Jacobi– Bellman (HJB) equations, the closed-loop optimal feedback control can hardly be obtained. Approximate optimal solutions of the optimal problem have consequently attracted much attention.[12– 16] Among those approximate approaches, the adaptive dynamic programming (ADP) algorithm, proposed by Werbos, [17, 18] has played an important role in seeking the approximate solutions of dynamic programming problems.[19– 21] There are several synonyms used for ADP, including adaptive critic designs, [22] adaptive dynamic programming, [23– 27] approximate dynamic programming, [28] neural dynamic programming, [29] and reinforcement learning.[30] In Refs. [22] and [28], ADP approaches were classified into several main schemes, which are heuristic dynamic programming (HDP), action-dependent HDP (ADHDP), dual heuristic dynamic programming (DHP), action-dependent DHP (ADDHP), which is also called Q-learning, [31] globalized DHP (GDHP), and action-dependent GDHP (ADGDHP). Iterative methods are also used in ADP to obtain the solution of the HJB equation indirectly and they have received increasing attention.[32– 40] There are two main iterative ADP algorithms, [41] which are based on value and policy iterations, respectively.
Value iteration algorithms for the optimal control of discrete-time nonlinear systems were given in Ref. [42]. Al-Tamimi and Lewis[43] studied the deterministic discrete-time affine nonlinear systems and a value iteration algorithm, which is referred to as HDP and proposed for finding the optimal control law. Starting from J[0](xk) ≡ 0, the value iteration algorithm is updated by

for i = 0, 1, 2, … c, where xk+ 1 = f(xk) + g(xk)u[i](xk). In Ref. [43], it was proved that J[i](xk) is a nondecreasing sequence and bounded, and hence converges to J* (xk). Zhang et al. applied a value iteration algorithm for optimal tracking problems.[36] Song et al. successfully implemented value iteration algorithms to find the optimal tracking control law for Hé non chaotic systems.[44] For most previous value iteration algorithms of ADP, the initial performance index function is chosen as zero.[36, 43, 44] For each of the iterative controls u[i](xk), i = 0, 1, … , the stability of the system cannot be guaranteed. This means that only the converged u* (xk) can be used to control the nonlinear system, and all the iterative controls u[i](xk), i = 0, 1, … may be invalid. So the computation efficiency of the value iteration ADP method is very low.
Policy iteration algorithms for the optimal control of continuous-time systems with continuous state and action spaces were given in Refs. [12] and [32]. In Ref. [12], Murray et al. proved that for continuous-time affine nonlinear systems, each of the iterative controls stabilizes the nonlinear systems by using the policy iteration algorithms. This is the great merit of the policy iteration algorithms. However, almost all of the discussions on the policy iteration algorithms are for continuous-time control systems.[35] In Ref. [45], the policy iteration algorithm for discrete-time systems was displayed and the stability and convergence properties were discussed. To the best of our knowledge, there is still no discussion focused on the policy iteration algorithms for the optimal tracking controls of discrete-time chaotic systems. This motives our research.
In this paper, inspired by Ref. [45], we develop a policy iteration ADP algorithm for the first time to solve the optimal tracking controls of discrete-time chaotic systems. First, by system transformations, the optimal tracking problem is transformed into an optimal regulation problem. Next, a policy iteration algorithm for discrete-time chaotic systems is described. Then, the convergence and admissibility properties of the developed policy iteration algorithm are presented, which show that the transformed chaotic system can be stabilized under an arbitrary iterative control law and simultaneously guarantee the iterative performance index function to converge to the optimum. By employing neural networks, the developed policy iteration algorithm is implemented. To justify the effectiveness of the developed algorithm, the simulation results using the policy iteration algorithm are compared with the results obtained by the traditional value iteration algorithm.
This paper is organized as follows. In Section 2, we present the problem formulation and preliminaries. In Section 3, the optimal chaotic tracking control scheme based on the policy iteration ADP algorithm is given, where the corresponding convergence and admissibility properties will also be presented. In Section 4, a simulation example is given to demonstrate the effectiveness of the developed optimal tracking control scheme. In Section 5, the conclusion is given.
Consider the following MIMO chaotic dynamic system:
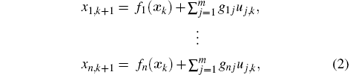
where xk = [x1, k, … , xn, k]T ∈ ℝ n is the system state vector which is assumed to be available from measurement. Let uk = [u1, k, … , um, k]T∈ ℝ m be the control input and gij (i = 1, … , n, j = 1, … , m) be the constant control gain. If we denote f(xk) = [f1(xk), … , fn(xk)]T and 

It should be pointed out that system (3) denotes a large class of chaotic systems, such as the Hé non systems[46] and the new discrete chaotic system proposed in Ref. [47]. In an optimal tracking problem, the control objective is to design optimal control u(xk) for system (2) such that the system state xk tracks the specified desired trajectory η k ∈ ℝ n, k = 0, 1, … , where η k satisfies
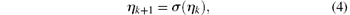
and σ is a given function. We define the tracking error as

and define the following quadratic performance index:

where Q ∈ ℝ n× n and R ∈ ℝ m× m are positive definite matrices and

be the utility function, where wk = uk − ue, k. Let ue, k denote the expected control introduced for analytical purpose, which can be given as

where g− 1(η k)g(η k) = I and I ∈ ℝ m× m is the identity matrix. Combining Eqs. (2) and (3), we obtain

We will study optimal tracking control problems for system (2). The goal is to find an optimal tracking control scheme which tracks the desired trajectory η k and simultaneously minimizes the performance index function (6). The optimal performance index function is defined as
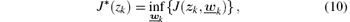
where

Then, the law of optimal single control vector can be expressed as

Hence, the HJB equation (11) can be written as
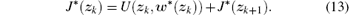
From Eqs. (4)– (13), we can see that the optimal tracking problem for chaotic system (3) is transformed into an optimal regulation problem for chaotic system (9). The objective of this paper is to construct an optimal tracking controller such that the chaotic system state xk tracks the reference signal η k, i.e., zk→ 0, as k→ 0. For convenience of analysis, the results of this paper are based on the following assumptions.
Assumption 1 The system (9) is controllable and the function 𝓕 (zk, wk) is Lipschitz continuous for ∀ zk, wk.
Assumption 2 The system state zk = 0 is an equilibrium state of system (9) under the control v = 0, i.e., F(0, 0) = 0.
Assumption 3The feed-back control wk = w(zk) satisfies w(zk) = 0 for zk = 0.
Assumption 4 The utility function U(zk, wk) is a continuous positive definite function of zk and wk.
Generally, J* (zk) is unknown before the control error wk ∈ ℝ m is considered. If we adopt the traditional dynamic programming method to obtain the optimal performance index function, then we have to face “ the curse of dimensionality” . This makes the optimal control nearly impossible to obtain by the HJB equation. So, in the next section, an effective policy iteration ADP algorithm will be developed to obtain the optimal chaotic tracking control iteratively.
In this section, a new discrete-time policy iteration algorithm is developed to obtain the optimal tracking control law for chaotic systems (2). The goal of the present iterative ADP algorithm is to construct an optimal control law w* (zk), k = 0, 1, … , which moves an arbitrary initial state x0 to the desired trajectory η k, and simultaneously minimizes the performance index function. Convergence and admissibility properties will be analyzed.
For optimal control problems, the developed control scheme must not only stabilize the control systems but also make the performance index function finite, i.e., the control law must be admissible.[43] We can define Ω w as the set of the admissible control laws, which is expressed as

Based on the above definition, we can introduce our policy iteration algorithm. Let i be the iteration index that increases from 0 to infinity. Let w[0](zk) ∈ Ω w be an arbitrary admissible control law. For i = 0, let J[0](zk) be the iterative performance index function constructed by w[0](zk), which satisfies the following generalized HJB (GHJB) equation:

For ∀ i = 1, 2, … , the developed policy iteration algorithm will iterate between
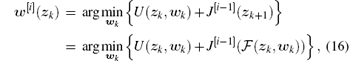
and
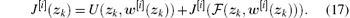
From Eqs. (15)– (17), we can see that the procedure of policy iteration is obviously different from value iteration (1). Thus, the convergence analysis for the value iteration algorithms in Refs. [36] and [43] is invalid for the policy iteration. Therefore, a new analysis will be given in this paper.
In Ref. [12], the convergence and admissibility properties of the continuous-time policy iteration algorithm are discussed. This shows that any of the iterative control laws can stabilize the transformed chaotic system. For the discrete-time systems, the proofs of the continuous-time policy iteration algorithms are invalid. Hence, a new analysis will be developed. We will show that for the discrete-time policy iteration algorithm, any of the iterative control laws can also stabilize the transformed system.
Theorem 1 For i = 0, 1, … , let J[i](zk) and w[i](zk) be obtained by Eqs. (15)– (17), where w[0](zk)∈ Ω w is an arbitrary admissible control law. Then, for ∀ i = 0, 1, … , the iterative control law w[i](zk) stabilizes the chaotic system (9).
Proof According to Eq. (17), we have

Let zk = 0, according to Assumption 3, we have w[i](zk) = 0. According to Assumption 2, we also have zk+ 1 = 𝓕 (zk, w[i](zk)) = 0 and furthermore w[i](zk+ 1) = 0. Then according to the mathematical induction and Assumption 4, we have ∀ U(zk+ j, w[i](zk+ j)) = 0, j = 0, 1, … , which shows J[i](zk) = 0 for zk = 0.
On the other hand, according to Assumption 4, the utility function U(zk, wk) is positive definite for ∀ zk, wk. Then we can get U(zk, wk) → ∞ as zk→ ∞ , which means J[i](zk) → ∞ . Hence, J[i](zk) is positive definite for ∀ i = 0, 1, … .
According to Eqs. (15) and (17), for ∀ i = 0, 1, … ,

holds. Then for ∀ i = 0, 1, … , J[i](zk) is a Lyapunov function. Thus w[i](zk) is a stable control law. The proof is completed.
Theorem 2 For i = 0, 1, … , let J[i](zk) and w[i](zk) be obtained by Eqs. (15)– (17). For ∀ zk ∈ ℝ n, the iterative performance index function J[i](zk) is a monotonically non-increasing sequence for ∀ i ≥ 0, i.e.,

Proof For i = 0, 1, … , define a new performance index function ϒ [i+ 1](zk) as

where w[i+ 1] (zk) is obtained by Eq. (16). According to Eq. (21), for ∀ zk, we can obtain

The inequality (20) will be proven by the mathematical induction. According to Theorem 1, for i = 0, 1, … , w[i+ 1](zk) is a stable control law. Then, zk→ 0, for ∀ k → ∞ . Without loss of generality, let zN = 0, where N→ ∞ . We can obtain
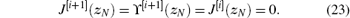
First, we let k = N – 1. According to Eq. (16), we have

According to Eqs. (17) and (24), we can obtain
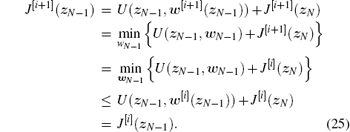
So, the conclusion holds for k = N – 1. Assume that the conclusion holds for k = l + 1, l = 0, 1, … . For k = l, we have

According to Eq. (22), for ∀ zl, we have

According to inequalities (26) and (27), for i = 0, 1, … , inequality (20) holds for ∀ zk. The proof is completed.
Corollary 1 For i = 0, 1, … , let J[i](zk) and w[i](zk) be obtained by Eqs. (15)– (17), where w[0](zk) is an arbitrary admissible control law. Then for ∀ i = 0, 1, … , the iterative control law w[i](zk) is admissible.
From Theorem 2, we can see that the iterative performance index function J[i](zk) is monotonically non-increasing and lower bounded. Hence as i→ ∞ , the limit of J[i](zk) exists, i.e.,

We can then derive the following theorem.
Theorem 3 For i = 0, 1, … , let J[i](zk) and w[i](zk) be obtained by Eqs. (15)– (17). The iterative performance index function J[i](zk) then converges to the optimal performance index function J* (zk) as i → ∞ , i.e.,

which satisfies the HJB equation (11).
Proof The theorem can be proven in two steps. Let μ (zk) ∈ Ω w be an arbitrary admissible control law. Define a new performance index function P(zk), which satisfies

For i = 0, 1, … , let J[i](zk) and w[i](zk) be obtained by Eqs. (15) and (16). We will then prove
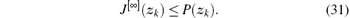
The statement (31) can be proven by a mathematical induction. As μ (zk) is an admissible control law, we have zk→ 0 as k → ∞ . Without loss of generality, let zN = 0, where N → ∞ . According to Eq. (30), we have

where zN = 0. According to Eq. (28), the iterative performance index function J[∞ ] (zk) can be expressed as

Since w[∞ ](zk) is an admissible control law, we can obtain zN = 0 when N → ∞ , which means J[∞ ](zN) = P(zN) = 0 as N → ∞ . For N– 1, according to Eq. (43), we can obtain
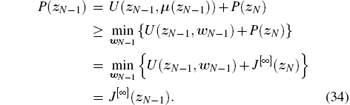
Assume that the statement holds for k = l+ 1, l = 0, 1, … , then for k = l, we have

Hence for ∀ zk, k = 0, 1, … , the inequality (31) holds. The mathematical induction is completed.
Next, we will prove that the iterative performance index function J[i](zk) converges to the optimal performance index function J* (zk) as i → ∞ , i.e.,

which satisfies the HJB equation (11).
According to the definition of ϒ [i+ 1](zk) in Eq. (21), we have

According to Eq. (26), we obtain
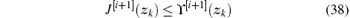
for ∀ zk. Let i→ ∞ . We obtain

Thus we can obtain
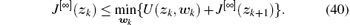
Let ε > 0 be an arbitrary positive number. Since J[i](zk) is non-increasing for i ≥ 1 and 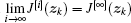

Hence, we can obtain

Since ε is arbitrary, we have
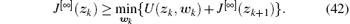
Combining Eqs. (40) and (42), we can obtain
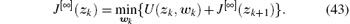
According to the definition of J* (zk) in Eq. (40), for ∀ i = 0, 1, … , we have

Let i → ∞ , we can then obtain

On the other hand, as μ (zk)∈ Ω w is arbitrary, if we let w[i](zk) = w* (zk), then according to inequality (31), we have

According to inequalities (45) and (46), we can obtain Eq. (36). The proof is completed.
Corollary 2 Let zk ∈ ℝ n be an arbitrary state vector. If Theorem 3 holds, then the iterative control law w[i](zk) converges to the optimal control law as i → ∞ , i.e., 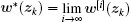
In the policy iteration algorithm (15)– (17), for ∀ i = 0, 1, … , we should construct an iterative performance index function J[i](zk) to satisfy Eq. (17). In this subsection, we will give an effective method to construct the iterative performance index function.
Let Ψ (zk) be a positive semi-definite function. Introducing a new iteration index j = 0, 1, … . Define a new performance index function 
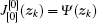

For i = 1, 2, … and j = 0, 1… , let

where 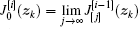
Theorem 4 Let Ψ (zk) ≥ 0 be an arbitrary semi-positive definite function. Let 
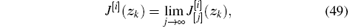
where J[i](zk) satisfies Eqs. (15) and (17), respectively.
Proof According to Eq. (47), we have
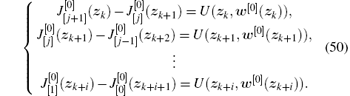
We can then obtain

Let j → ∞ . We can obtain

Since w[0] (zk) is an admissible control law, 


To evaluate the performance of our policy iteration algorithm, we choose an example with quadratic utility functions for numerical experiments. Consider the following chaotic system:[4]
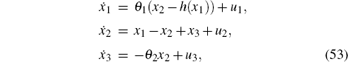
where h(x1) = m1x1 + (m0 − m1)(| x1 + θ 3| − | x1 − θ 3| )/2, θ 1 = 9, θ 2 = 14.28, θ 3 = 1, m0 = − 1/7, and m1 = 2/7. The state trajectory of the chaotic system is given in Fig. 1. According to Euler’ s discretization method, the continuous time chaotic system can be represented as follows:


where Δ T = 0.1. Let the desired orbit be η k = [sin(k), 0.5cos(k), 0.6sin(k)]T and the initial state be selected as [1, − 1, 1.5]T. The utility function is defined as 
 | Fig. 1. The chaotic attractor of system (54). |
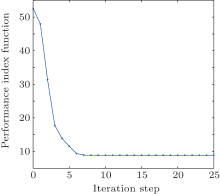
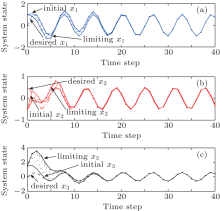
The critic network and the action network are chosen as three-layer BP neural networks with the structures of 3– 10– 1 and 3– 10– 3, respectively. For each iteration step, the critic network and the action network are trained for 1000 steps using a learning rate of α = 0.02 so that the neural network training error becomes less than 10− 5. The training methods of the neural networks have been described in Refs. [30] and [45], which are omitted here. The performance index function is shown in Fig. 2. The system states are shown in Fig. 3. The state errors are given in Fig. 4. The iterative controls are shown in Fig. 5. In the simulation results, we let “ initial” and “ limiting” denote the initial iteration and the limiting iteration, respectively.
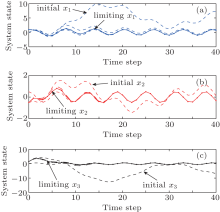
From the simulation results, we can see that the iterative performance index function J[i](zk) is monotonically non-increasing and converges to the optimal performance index function. For ∀ i = 0, 1, … , the regulation system (9) is stable under the iterative control law w[i](zk). To show the effectiveness of the developed algorithm, the results of our developed policy iteration algorithm are compared with the results using a value iteration algorithm.[36] Let the value iteration algorithm be implemented by Eq. (1), where the initial performance index function J[0](zk) ≡ 0. All of the parameters are set the same as those for implementing the polity iteration algorithm. The performance index function is shown in Fig. 6. The system states are shown in Fig. 7. The iterative controls are shown in Fig. 8.
From Fig. 6, we can see that the iterative performance index function is monotonically non-decreasing and converges to the optimum. The convergence properties of value and policy iteration algorithms are inherently different. On the other hand, from Figs. 7 and 8, we can see that there exit unstable system states and control laws in the value iteration algorithm. From Figs. 3 and 5, we can see that the chaotic system (54) can track the desired trajectories with the policy iteration algorithm, which illustrates the effectiveness of the developed algorithm.
We have developed an optimal tracking control method for chaotic systems by policy iteration. By system transformations, the optimal tracking problem is transformed into an optimal regulation one. Next, the policy iteration algorithm for the transformed chaotic systems are presented. The convergence and admissibility properties of the developed policy iteration algorithm are presented, which show that the transformed chaotic system can be stabilized under the present iterative control law and the iterative performance index function simultaneously converges to the optimum. Finally, the effectiveness of the developed optimal tracking control scheme for chaotic systems is verified by a simulation.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|