The properties of magnetic thin films grown on silicon have been investigated by amounts of work in the past decades, because of their applications in the integration of magnetic devices in silicon technology and new opportunities in spintronics, ^{[1, 2]} especially the magnetization reversal process of iron films.^{[3– 5]} For an Fe (001) film, the domain wall displacement always dominates the magnetization reversal process and sometimes coherent rotation will participate in the reversal process in a high external field or near the easy axis of film.^{[6, 7]} The magneto-optic Kerr effect (MOKE) is always one of the prior choices to explore the detailed information, but the complicated optical path restricts its application in micro-devices. At the same time, the transport measurement has been developed for decades and has widely been used in silicon-based devices.^{[8, 9]} So it is necessary to investigate the magnetization reversal process of Fe/Si (001) film by the planar Hall effect (PHE).

In our previous work, the MOKE was chosen to investigate the domain wall displacement process of Fe/Si (001) film. Different domain wall displacement processes can be induced in one hysteresis loop with a weak bias field.^[10] Furthermore, we find that the magnetization reversal process of Fe/Si (001) film has been proved to be the combination of coherent rotation and domain wall displacement when the external field is smaller than the anisotropy field by torque measurement with anisotropic magnetoresistance.^[11] In the present work, the 40-ML single crystal iron film is reported to be grown on a vicinal Si (001) substrate using a flat ultrathin c(2 × 2) iron silicide seed layer and the PHE is used to investigate the magnetization reversal process and determine the domain wall pinning energy. The magnetization reversal process is found to be dominated by different mechanisms at different external field angles. The fitting results of domain wall pinning energy by planar Hall resistance (PHR) show good consistency with the theoretical model.

The sample was grown on a Si (001) substrate using an ultrahigh vacuum molecular beam epitaxial (MBE) chamber equipped with low-energy electron diffraction (LEED). The Si (001) substrate was first well baked out and then flashed, and the well-fined Si (001)-2× 1 surface was obtained.^[12] Then, the buffer layer was deposited on the wafer by e-beam bombardment with 2 ML of Fe (99.999% purity), and annealed at 550 ° C for 5 minutes.^[13] This procedure gives a highly ordered 2× 2 periodic iron silicide structure to prevent the Fe/Si intermixing. The 40-ML Fe film was deposited on the iron silicide template. The epitaxial relationships among the Fe layer, the iron silicide template, and the Si (001) substrate are as follows:^{[13, 14]} Fe(001)∥ c(2 × 2)FeSi₂(001)∥ Si (001) and Fe [100]∥ c(2 × 2)FeSi₂[010]∥ Si[110]. A nonmagnetic Cu layer with a thickness of 25 ML was deposited on the sample as a capping layer to protect the sample from being oxidized. In the process of growth, the base pressure was around 2 × 10^{− 10} mbar (1 bar = 10⁵ Pa) and the substrate was kept at room temperature. After the MOKE measurements, photolithography was used to etch the sample into an 8-probe Hall geometry with the long axis oriented along the Fe [110] axis. The PHR was measured in the direction perpendicular to the current and the current applied to the sample was 5 mA.

Figure 1(a) shows the coordinate system used in MOKE and PHE measurements. The current flows in the Fe [110] direction, so that the PHE effect can obtain its maximum or minimum value at an easy axis where the magnetization prefers to stay. We measure the Hall voltage V_xy perpendicular to the current direction to calculate the PHR. θ and φ are the angles of magnetization and external field with respect to the Fe [100] axis direction, respectively. Figure 1(b) shows the LEED pattern of the iron film grown on the Si (001) substrate. The sharp cubic symmetric spots of the LEED pattern indicate the bcc structure iron film with a thickness of 40 ML.^{[12, 15]}

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Coordinate system used in MOKE and PHE measurements, and (b) LEED pattern of 40-ML iron film grown on a Si (001) substrate.

The hysteresis loops of the Fe/Si (001) film are first measured by MOKE. Figure 2 shows the typical hysteresis loops at external field angle φ = 0° , 9° , 36° , and 45° , respectively. The loop at φ = 0° is a typical 1-jump magnetization reversal process induced by 180° domain wall displacement, and the hysteresis loop at φ = 36° is a typical 2-jump magnetization reversal process induced twice by 90° domain wall displacement, respectively.^[16] The slight unsymmetry of the loop may be induced by the influence of the weak field from the surroundings.^[10] Though the hysteresis loop at φ = 0° seems to be saturated and the one at φ = 45° seems to be hard to reach saturation, they both show the 1-jump magnetization reversal process. They should have different meanings, because the directions of the external field are at the easy axis and hard axis, respectively. Furthermore, we cannot judge whether the loop at φ = 9° is a 1 or 2-jump magnetization reversal process. Apparently, the magnetization almost stays near the easy axis, because the loops do not show any coherent rotation information and the easy axis is the minimum energy position of the system. When φ = 9° and the external field reaches a positive maximum, the magnetization stays in the Fe [100] direction. 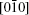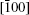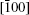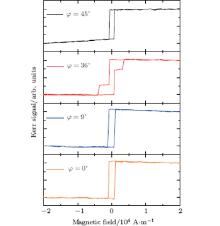As the external field decreases, the magnetization jumps to the Fe direction preferentially in energy and then jumps to the Fe direction for the 2-jump process or jumps to the Fe direction directly for the 1-jump process. For the 2-jump process, the external field range of the magnetization staying at Fe [010] or Fe axis depends on the system energy. The MOKE signal is in direct proportion to cos (θ − φ ), ^[17] if magnetization stays at Fe [010] or Fe axis too short a time, we cannot observe the 2-jump process. The PHE measurement may overcome this shortage.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Typical hysteresis loops of the Fe/Si (001) film, measured by MOKE at external field angle φ = 0° , 9° , 27° , 36° , and 45° , respectively.

In a single crystalline system, the PHR can be expressed as^[9]

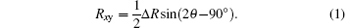
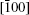
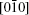
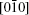
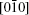
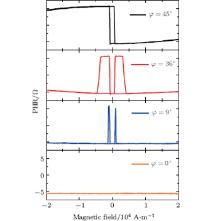Unlike the MOKE measurement, the variation of the PHR value is twice as fast. That is to say, the PHR reaches its minimum value in the Fe [100] or Fe direction, and its maximum value in the Fe [010] or Fe direction. For the 90° or 180° domain wall magnetization reversal process, we can judge it from the PHR curve directly. Figure 3 shows the corresponding PHR curves at φ = 0° , 9° , 36° , and 45° . It is obvious that the PHR curve at φ = 0° presents a 1-jump process with 180° domain wall displacement and the PHR curves at φ = 9° , 27° , and 36° exhibit the 90° domain wall magnetization reversal processes. For the curve at φ = 45° , the PHR value changes to maximum at the external field H = ± 800 A/m and does not change to minimum at the negative maximum field, which indicates that it needs an even higher field to saturate the iron film. The magnetization only switches to Fe [010] or Fe axis and rotates around Fe [010] or Fe axis, when the external field increases from the negative field, it switches to Fe [100] again. The curve at φ = 0° is a straight line, which does not mean that the magnetization stays static. Because the 1-jump process is dominated by 180° domain wall displacement, according to Eq. (1) the value R_xy will not change when the direction of magnetization θ changes 180° . The advantage of PHE measurement is proved at φ = 9° compared with the corresponding hysteresis loop by MOKE measurement. There are two sharp peaks at the coercivity position by PHE measurement, nevertheless the hysteresis loop does not show a clear hesitation near the coercivity position by MOKE. That is because the value of PHR has significantly changed when the direction of magnetization changes 90° . Therefore, the PHE can be used to identify the 90° domain wall and 180° domain wall displacement with higher accuracy than MOKE measurement. It can also help to determine the domain wall pinning energy. At high fields of hysteresis loops at φ = 36° and 45° , the curves do not show a horizontal line compared with the hysteresis loops at φ = 0° and 9° , they are lines with a bit of an incline, which indicates that the coherent rotation happens at high field in the single crystalline iron film.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Typical PHE curves at external field angle φ = 0° , 9° , 27° , 36° , and 45° , respectively.

As the thin film epitaxially grows on substrates, it may induce a weak uniaxial magnetic anisotropy (UMA) because of the stress, lattice mismatch or other effects.^{[18– 20]} Here, we consider the first cubic magnetocrystalline anisotropy (MCA), the UMA, and the Zeeman energy for Fe/Si (001) film. In general, the orientation of the UMA can be along any direction, so we separate it into two components: K_u1 along Fe [100] and K_u2 along Fe [110].^[21] The total free energy density of the system with an external field H is described as

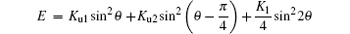
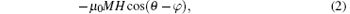
where the first and the second terms are the UMA energies along the directions [100] and [110], respectively. The third term is the first cubic MCA energy. The fourth term is the Zeeman energy of external fieldH. K_u1 and K_u2 are the UMA constants and K₁ is the first cubic MCA constant. M is the saturation magnetization of iron.

The magnetization will always rotate to a local minimum energy E(θ ) for a given field when it obeys the Stoner– Wohlfarth model. However, the magnetization will be unpinned and switched to another local minimum energy due to the existence of domain structure.^{[22, 23]}

In the previous work, the UMA in Fe/Si (001) is very small compared with the MCA and the domain wall pinning energy.^{[10, 11]} Due to the existence of K_u2, the local minima position will shift a small angle δ , so we set the local minima of Eq. (2) to be at θ = − δ , 90° + δ , 180° − δ , and 270° + δ , where 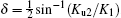.^{[24, 25]} According to Refs. [25] and [26], in the range φ = 0° – 45° , we can calculate the coercivity field of the magnetization reversal process.

For the 1-jump process,

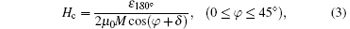
and for the 2-jump process,

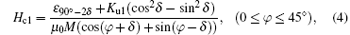
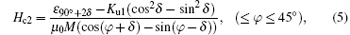
where ε _{90° − 2δ} , ε _{90° + 2δ} , and ε _180° are the pinning energies for the 2-jump and 1-jump magnetization reversal process.

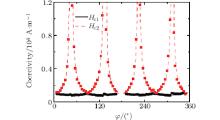
For other ranges of φ we can calculate the coercivity expressions in different ranges of external fields by changing the angle in steps of 45° . Figure 4 shows the fitting results of Eqs. (4) and (5) from the PHE measurement. As the PHE can only show the coercivity of the 90° domain wall displacement process, no coercivity is induced by the 180° domain wall displacement. It is an excellent correspondence between theoretical calculations and experimental measurements. Also, we can calculate the domain wall pinning energies ε _{90° − 2δ} /μ ₀M = 1.03 × 10³ A/m, ε _{90° + 2δ} /μ ₀M = 1.15 × 10³ A/m, δ = − 0.5° , and K_u1/μ ₀M = − 80 A/m. We can also calculate the domain wall pinning energy from the hysteresis loops from the MOKE measurement, which is consistent with the one from the PHR measurement, and ε _180° /μ ₀M = 1.83 × 10³ A/m. As predicted in Ref. [16], 2ε _90° > ε _180° will induce a 1-jump magnetization reversal process in a certain angular range, and this range depends on how much greater than ε _180° the 2ε _90° is. Here, the values of 2ε _{90° − 2δ} and 2ε _{90° + 2δ} have no big difference from ε _180° , which explains why there exists so wide an angular range of the 2-jump switching process.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Experimentally measured coercivities (points) by PHE and the fitted values (lines).

In this paper, we investigate the magnetization reversal process of 40-ML iron films grown on Si (001) substrates. The MOKE measurement shows typical 90° and 180° domain wall displacements when scanning the external field. However, the linear feature of MOKE measurement leads to an indistinct area between these two domain wall displacements at certain external field angles. The PHE overcomes this shortage, and shows clearly the magnetization reversal process. Especially, there are both coherent rotation and domain wall displacement near the hard axis. The domain wall pinning energy and UMA can also be determined accurately from the MOKE and PHE measurements.