Corresponding author. E-mail: xiongrui@whu.edu.cn
Project supported by the Agence Nationale de la Recherche through Grant PNICTIDES.
We report electronic Raman scattering measurements on Ba(Fe1− xCo x)2As2 ( x = 0.065 and 0.2) single crystals with Raman shifts from 9 cm−1 up to 600 cm−1 in the symmetry of B1g with respect to 1 Fe unit cell. When the crystals are cooled down, the evident quasielastic peaks of Raman spectra occur only in the crystal with x = 0.065, which is due to the contribution of orbital ordering between xz and yz Fe 3d orbitals, as we reported in another work. Here, we analyze the Eg phonon at 128 cm−1, which has the same function form of its Raman tensors as those of xz and yz Fe 3d orbitals in these two crystals respectively. Unlike their electronic continuums, no anomalies are found in the Eg phonons of these two samples, which simply follows the expressions corresponding to the anharmonic phonon decay into acoustic phonons with the same frequencies and opposite momenta. Our results indicate that the structural and magnetic phase transition might be completely suppressed by chemical doping and there is not any indication of coupling between charge nematicity and Eg phonon mode from our experimental results, which is consistent with the results in our previous work.
Discovery of superconductivity with a transition temperature up to 26 K in LaFeAsO1− xFx[1] activates the enthusiasm of research on a brand new family of high-Tc superconductors based on iron-arsnide superconducting layers. According to their chemical formula, two main groups of iron pnictides are categorized as the 1111 system (LaFeAsO1− xFx) and 122 system (BaFe2As2 and its doping compounds[2, 3]). All these compounds undergo a similar phase transform. The Ba122 system is one of the most extensively studied systems in iron pnictides. The undoped compounds each exhibit a spin density wave (SDW) phase, which are not Mott insulators like cuprates but bad metals with high resistivities. Upon doping with electrons or holes, the magnetic order and its associated structural transition are suppressed and a superconductive state emerges. The relationships among magnetic order, lattice dynamics, and superconductivity seem to be a key to unveiling the mechanism of the superconductivity of iron pnictides. It is suggested that the structural transition is driven by electrons because of the anomalies of the phonon splitting in tetragonal-orthorhombic lattice distortion[4, 5] and the much larger anisotropy resistivity than the anisotropy of the lattice parameters, [6] which may be driven by the same fluctuations that give rise to the superconductivity.
A more careful examination of the phase diagram revealed that there is another non-superconducting order state besides magnetism, [7] which is characterized as the nematic phase. Similar electronic states, in which rotational symmetry is broken but translational invariance is preserved, have been proposed in a variety of relevant materials, [8] such as quantum Hall systems, [9] cuprates, [10, 11] ruthenates, [12] and heavy fermions.[13] The observation of charge nematic fluctuations was reported in our previous studies, [14, 15] which exhibit a quasielastic peak in electronic Raman scattering due to the contribution of orbital ordering between xz and yz Fe 3d orbitals.
Here we choose two cobalt-doped BaFe2As2 compounds with x = 0.065 and 0.2, in which structural transitions are all completely suppressed but charge nematic fluctuations are preserved in the compound with x = 0.065. Eg mode phonons, having the same function form as those of the xz and yz Fe 3d orbitals and associated with the displacements of Fe and As atoms in the ab planes, are extracted from the Raman spectra of the two compounds respectively.
Single crystals of Ba(Fe1− xCox)2As2 with x = 0.065 and 0.2 were grown by a self-flux method through high-temperature solid-state reactions as described elsewhere.[16] Raman experiments were carried out using a diode-pumped solid state laser emitting at 532 nm and a triple grating spectrometer (JY-T640000) equipped with a nitrogen cooled CCD camera. In order to extract the imaginary part of the Raman response function, the raw spectra were corrected for the Bose factor and the instrumental spectral response. All temperatures were corrected for the estimated laser heating. It was first estimated by making a comparison between the power dependence and temperature dependence of the phonon frequencies. This estimate was then cross-checked by monitoring the onset of Rayleigh scattering by orthorhombic structural domains across the structural transition temperature. Both methods yielded an estimated heating of 1 K± 0.2 per mW of incident power.
We use the crossed polarization configuration (es ⊥ ei) almost along the diagonal of 1 Fe unit cell as shown in Fig. 1. We note that photons can probe ab-plane polarized phonons because of the finite projection of their polarization along the c axis.
Figure 2 shows the Raman spectra for Ba(Fe1− xCox)2As2 with x = 0.065 and 0.2 in B1g configuration with respect to 1 Fe unit cell at selected temperatures. It is clear that the Raman responses each keep increasing and generate an apparent quasielastic peak at low frequencies with temperature cooling down in the sample x = 0.065, indicating that there exist charge nematic fluctuations due to the contribution of xz and yz Fe 3d orbital ordering (described concretely in Ref. [14]) in the absence of structural and magnetic transitions.[5, 16] While it seems that nothing happens in the sample x = 0.2 at diverse temperatures.
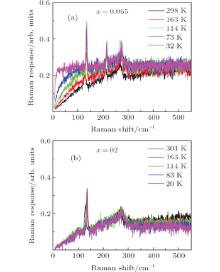 | Fig. 2. Raman spectra for Ba(Fe1− xCox)2As2 with x = 0.065 (a) and 0.2 (b) respectively in B1g configuration with respect to 1 Fe unit cell at selected temperatures. |
On the other hand, three phonon peaks (at about 130 cm− 1, 212 cm− 1, and 264 cm− 1) and two phonon peaks (at about 130 cm− 1 and 264 cm− 1) can be seen in the spectra of the sample with x = 0.065 and x = 0.2 respectively. Ba(Fe1− xCox)2As2 with x = 0.065 and x = 0.2 are in the tetragonal I4/mmm space group, the same as the parent compound BaFe2As2 above Neel temperature TN. The irreducible vibrational representation is[17]

Of these, only A1g, B1g, and Eg are Raman-active phonon modes as shown in Table 1 in Ref. [19]. According to the polarization selection rules, the A1g mode is visible in the spectra only when the incident polarization ei and outgoing polarization es are parallel, so we cannot find an A1g phonon mode in Fig. 2 due to the crossed polarization configuration (ei ⊥ es) we used. The intensity of the B1g mode depends on the angle α between ei and the a axis (1 Fe unit cell), being proportional to cos22α . Compared with the result in previous work, [18] the sharp peak at about 212 cm− 1 in Fig. 2 should be the B1g phonon mode, which should not exist in the B1g configuration, because it is difficult to make the polarization exactly be along the diagonal (α = 45° ) of the Fe square, resulting in the leakage of the signal from the B2g channel (α = 0). It is obvious that this leakage is very little because the intensity of the B1g phonon here is much smaller than the B2g channel. Otherwise, there is not any quasielastic peak existing in the spectra of the B2g channel, [14] therefore, this little leakage does not affect our analysis. Two Eg phonons are visible at about 130 cm− 1 and 264 cm− 1 respectively because of the finite projection of their polarization along the c axis.
The Raman tensors of the Eg phonon mode are given as
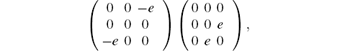
which have the same function form and symmetry as xz and yz Fe 3d orbitals. Furthermore, unlike B1g and A1g modes, which are the pure modes involving the displacements of Fe and As atoms along the c axis respectively, Eg modes are strongly mixed modes involving the displacements of both Fe and As atoms in the ab planes.[18] On the other hand, the five d orbitals of Fe atoms split into two groups, t2g (dxy, dxz, dyz) and eg (dx2− y2, d3z2− r2) at different energy levels respectively due to the crystal fields of the tetrahedron composed of four neighboring As atoms. Three of five orbitals, dxy, dx2− y2, and d3z2− r2 are rotationally symmetric in the ab plane, which do not have the potential to contribute to the anisotropy properties in the ab plane, such as structural transition and nematic order, therefore, the other two degenerate orbitals dxz and dyz are the only possible candidates to have an effect on the asymmetric properties in the ab plane. It is suggested that uneven occupations of the dxz and dyz orbitals make the orthorhombic crystal structure more energetically favorable, thus inducing the structural phase transition.[19] In addition, anomalies in Eg mode phonon splitting in underdoped samples, which undergo a structural transition upon the temperature cooling down, imply an electron driven structural transition.[18] So the Eg phonon mode might play an important role in the interaction between electron and lattice in Ba(Fe1− xCox)2As2 compounds.
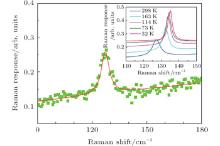
The green scatter in Fig. 3 is the room temperature Raman response in the range from 90 cm− 1 to 180 cm− 1 of the sample with x = 0.065, which has an apparent charge nematic fluctuation as the temperature cools down. It exhibits a symmetric and typical Lorentz-like peak (Eg mode phonon), indicating a weak coupling between the phonon mode and the electronic continuum. In order to study the Eg phonon mode quantitatively, we fit the peak at all temperatures by using a Lorentz term and a linear term, which is written as
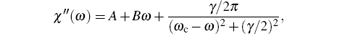
where ω c is the resonant frequency of the Lorentz oscillator. The line width of the phonon peak is characterized by γ in the third term on the right-hand side of the above expression. The solid smooth line through the data in Fig. 3 is the fitting line, and more fitting lines at different temperatures are shown in the inset of Fig. 3. It is clear that the frequency of the phonon peak exhibits a monotonic increase as temperature decreases, and shows no signs of splitting, indicating the structural phase transition is completely suppressed in the Ba(Fe1− xCox)2As2 (x = 0.065) compound.
We extract all the peak positions ω c(T) and the line widths γ (T) at different temperatures in two samples as shown in Fig. 4. Simple expressions corresponding to the anharmonic phonon decay into acoustic phonons with the same frequencies and opposite momenta are as follows:[20, 21]
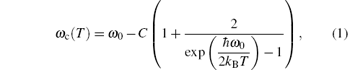
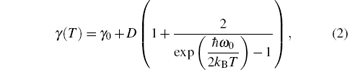
where C and D are the positive constants, ω 0 is the bare phonon frequency, and γ 0 is a residual temperature-independent line width. The positions and line widths of the Eg phonon at about 130 cm− 1 of the sample with x = 0.065 are well fitted by Eqs. (1) and (2) with ω 0 = 138.8 cm− 1 and γ 0 = 1.489 cm− 1, and on the other side, ω 0 = 140.77 and γ 0 = 1.796 cm− 1 for the sample with x = 0.2.
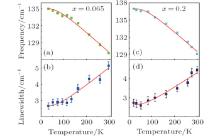 | Fig. 4. Peak position and line width (full width at half maximum), respectively, of the Eg mode at 130 cm− 1. Solid smooth curves through the data are fit to Eqs. (1) and (2). |
Comparing the evolutions of the Eg mode phonon with the temperature in two samples, we cannot find any anomalies[22] and intrinsic differences, which indicate that the structural and magnetic phase transitions might be completely suppressed by chemical doping. Furthermore, as in the previous discussions, we cannot find any indications of the coupling between enhanced charge nematic susceptibility/orbital order and Eg phonon mode in Ba(Fe1− xCox)2As2 compounds. The coupling of charge/orbital, spin and lattice is very complicated[23] and a more clear picture of the coupling between them needs further study.
We investigate the temperature-dependent Raman scattering of Eg mode phonon in Ba(Fe1− xCox)2As2 (x = 0.065 and 0.2). There exists an apparent quasielastic peak only for x = 0.065, indicating a charge nematic fluctuation due to the contribution of the orbital order between xz and yz Fe 3d orbitals, which have the same function form of Eg modes. The symmetric line shape of this phonon in the Raman response implies a very weak coupling between the phonon and the electronic continuum. Also, no anomalies can be found in the Eg phonon mode of samples with or without charge/orbital fluctuations, indicating that structural and magnetic phase transitions might be completely suppressed by chemical doping.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|