Pulse decomposition-based analysis of PAT/TAT error caused by negative lobes in limited-view conditions<xref ref-type="fn" rid="cpb141318fn1">*</xref>

Cite this Article

Liu Liang-Bing, Tao Chao, Liu Xiao-Jun, Li Xian-Li, Zhang Hai-Tao. Pulse decomposition-based analysis of PAT/TAT error caused by negative lobes in limited-view conditions* . Chinese Physics B, 2014, 24(2): 024304 Copy to clipboard

Permissions

Pulse decomposition-based analysis of PAT/TAT error caused by negative lobes in limited-view conditions*

Liu Liang-Bing^a),^b), Tao Chao^a)†, Liu Xiao-Jun^a)‡, Li Xian-Li^b), Zhang Hai-Tao^b)

a)Key Laboratory of Modern Acoustics, Nanjing University, Nanjing 210093, China

b)Logistical Engineering University, Chongqing 401311, China

†Corresponding author. E-mail: taochao@nju.edu.cn

‡Corresponding author. E-mail: liuxiaojun@nju.edu.cn

*Project supported by the National Basic Research Program of China (Grant No. 2012CB921504), the National Natural Science Foundation of China (Grant Nos. 11274167, 11274171, 61201450, 61201495, and 61302175), and the Chongqing Science and Technology Commission of China (Grant Nos. 2012jjA40058 and 2012jjA40006).

Abstract

Pulse decomposition has been proven to be efficient to analyze complicated signals and it is introduced into the photo-acoustic and thermo-acoustic tomography to eliminate reconstruction distortions caused by negative lobes. During image reconstruction, negative lobes bring errors in the estimation of acoustic pulse amplitude, which is closely related to the distribution of absorption coefficient. The negative lobe error degrades imaging quality seriously in limited-view conditions because it cannot be offset so well as in full-view conditions. Therefore, a pulse decomposition formula is provided with detailed deduction to eliminate the negative lobe error and is incorporated into the popular delay-and-sum method for better reconstructing the image without additional complicated computation. Numerical experiments show that the pulse decomposition improves the image quality obviously in the limited-view conditions, such as separating adjacent absorbers, discovering a small absorber despite disturbance from a big absorber nearby, etc.

Keyword: 43.60.+d; 44.05.+e; 43.35.+d; photo-acoustic tomography; thermo-acoustic tomography; limited-view; pulse decomposition; image reconstruction

Show Figures

1. Introduction

Pulse decomposition refers to dividing a synthesized wave into a set of constituent pulses, ^{[1– 4]} and then makes a complex phenomenon understood more easily.^{[1, 5, 6]} For example, a segment of a typical electrocardiogram (ECG) wave can be decomposed into a sum of several constituent Gaussian pulses with various amplitudes, sharpness, and time positions, which respectively represent working conditions of primary systole, kidney, and ilium, etc.^{[1, 5]}

Pulse decomposition has been successfully used in not only ECG signal analysis, ^{[4, 5]} but also the study of gamma-ray burst time profiles, ^[7] image processing, ^{[2, 3]} topographic mapping by airborne lasers, ^[6] etc. It has proved to have practical potential to draw a clear distinction of contributions made by plenty of constituent pulses, which is also necessary in image reconstruction of photoacoustic tomography (PAT)^{[8– 12]} and thermoacoustic tomography (TAT).^{[13– 16]}

PAT/TAT imaging is an emerging imaging technology in biomedicine, physically combining the functional contrast of optical imaging with the high resolution of ultrasonography. In photoacoustic (PA) and thermoacoustic (TA) pulses, negative lobes are the second half of the derivative of the illumination pulse.^[17] Sometimes, because of wave superposition, negative lobes of an acoustic pulse emanated from a big absorber may entirely suppress a pulse emanated from a small absorber nearby. This kind of energy neutralization in a certain propagation direction has not received much attention, because the errors in calculation of the acoustic pulse amplitude caused by it are offset by each other in full-view conditions.

However, in limited-view conditions, energy neutralization caused by negative lobes cannot be offset and then degrade the imaging quality seriously. Actually, limited-view conditions^{[14, 16, 18– 20]} occur quite frequently because of practical constraints due to the imaging hardware, scanning geometry, or ionizing radiation exposure. Aiming at this problem, some image reconstruction techniques such as the total variation (TV) method, ^{[16, 18– 20]} involved in the compress sensing (CS) theory, are adopted successfully by minimizing TV of reconstructed images iteratively because the image intensity does not change dramatically in most PAT applications. Similarly, we adopt the idea of pulse decomposition as a signal processing tool to divide the acoustic waves into a set of acoustic pulses, and then the negative lobe errors will be eliminated fundamentally in principle.

In this paper, we will give a pulse decomposition formula for acoustic waves with its mathematical deduction, and then combine it with the DAS algorithm to reconstruct the PAT and TAT image.

Furthermore, numerical experiments in limited-view conditions are conducted to measure improvement of the new method quantitatively, such as separating a pair of adjacent circles, discovering a small circle despite disturbance from a big circle nearby, etc.

2. Negative lobes caused error in pulse amplitude estimation

In response to energy absorption, the acoustic pressure, p(r, t), at position r, and time t in an acoustically homogeneous liquid-like medium obeys the following equation (with ignoring thermal diffusion and kinematic viscosity):

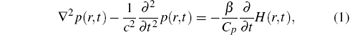
where H(r, t) is the heat energy deposited per unit time per unit volume, C_p is the specific heat, and β is the isobaric volume expansion coefficient. In general, the solution to Eq. (1) in the time domain can be described by

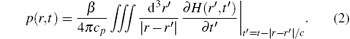
Obviously, the heating function is the product of a spatial absorption coefficient, A(r), and a temporal heating function, I_e(t). Thus, H(r, t) = A(r)I_e(r), and A(r) is closely related to p(r, t). As a result, there is a simplified formula of the delay-and-sum (DAS) reconstruction algorithm for PAT/TAT

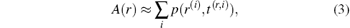
where r⁽ⁱ⁾ is the position of the i-th detector, t^{(r, i)} = | r– r⁽ⁱ⁾| /c + t̃ /4, and t̃ is the pulse duration of I_e(t).

Next, the following equation shows a deep insight into p(r₀, t₀), a point value at time t₀, recorded by a detector at position r₀:

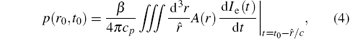
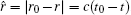
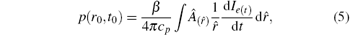
where . Then, the integration with respect to solid angle, Ω , is performed in Eq. (4), to describe the effect of A(r) directly as follows:

where .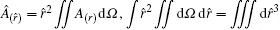

According to the above equations, we can find the following points:

(i) in Eq. (4) is the distance between a detector and an absorber element, which can be used to divide the region under test into different subsections, such as one-dimensional (1D) arcs, two-dimensional (2D) sector rings (as shown in Fig. 1(a)), and three-dimensional (3D) spherical shell.

(ii) Take 2D imaging for example. in Eq. (5) can be regarded as joint contributions to p(r₀, t₀) from many absorbers distributed in the same sector ring with away from the i-th detector.

(iii) t^{(r, i)} in Eq. (3) represents the time of the peak value in I_e(t) arriving at the i-th detector as shown by t_j (j ∈ [1, 3]) in Fig. 1(b). Moreover, p(r⁽ⁱ⁾, t^{(r, i)}) acts as an index of the pulse amplitude, and is assumed to be approximately proportional to A(r), or indeed .

(iv) I_e(t) represents the heating pulse, and the second half part of dI_e(t)/dt is negative, as shown by G in Fig. 1(c). Therefore, the negative lobes of acoustic pulses may bring errors in pulse amplitude estimation.

Figure Option
View Download New Window

Fig. 1. (a) All absorbers in the circular region under test are distributed into three sector rings centred at the i-th detector. (b) Absorbers in the j-th sector ring each emanate an acoustic pulse g^{(i, j)}, and t_j is the peak time of g^{(i, j)}, p⁽ⁱ⁾ is the i-th acoustic wave recorded by the i-th detector, and indeed

. (c) Three acoustic pulses have an identical waveform with the unit pulse G.

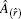
To demonstrate errors in pulse amplitude estimation caused by negative lobes, the measurement geometry shown in Fig. 1 is taken for example. All absorber elements are distributed in three sector rings centred at the i-th detector. Acoustic pulses emanated from all absorbers in the j-th sector ring are completely synchronizing signals and able to be combined into a pulse, g^{(i, j)}, when the thickness of every sector ring is equal and small enough. 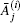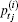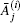Also, the amplitude , the positive peak value of g^{(i, j)}, is proportional to of the j-th sector ring. In some image reconstruction methods, ^{[8, 21– 24]}, a point value in the acoustic wave p⁽ⁱ⁾, is selected as the estimation of , and t_j is the positive peak time of g^{(i, j)}.

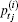
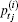
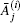
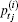
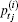
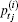
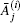
However, p⁽ⁱ⁾ is a synthetic wave and is always a joint effect of many acoustic pulses.^[25] Thus, there may be an obvious difference between and , ^[23] when negative lobes of other acoustic pulses lasting at time t_j have a much greater influence on . As shown in Fig. 1, when j ∈ (2, 3), the negative lobe of g^{(i, 1)} plays a much more important role in determining . Consequently, is negative and much different from .

For this reason, pulse decomposition is introduced to provide 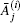more accurately by dividing p⁽ⁱ⁾ as a set of acoustic pulses g^{(i, j)}, of which positive peak value can be regarded as a more precise estimation of and A(r).

3. Pulse decomposition of an acoustic wave

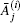
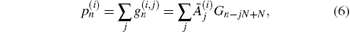
The basic idea of pulse decomposition to estimate the positive peak value of an acoustic pulse, , can be presented as follows:

where 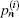is the n-th element of p⁽ⁱ⁾, and all g^{(i, j)} with varying j have the same envelopment as G, because the thickness value of these sector rings can be set to be equal and small enough; N is the delay time between the peak times of two adjacent pulses, such as g^{(i, j)} and g^{(i, j+ 1)}. Thus, N can be computed based on the thickness of a sector ring.

As indicated in Eq. (6), each point of p⁽ⁱ⁾, in some sense, is determined by all acoustic pulses. Differences among acoustic pulses lie in the amplitude 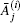, and delay time as shown in (n– jN+ N), the subscripts of G; furthermore, because the negative lobe of G is caused by shrinkage before absorbers return to original sizes after thermal expansion, the detailed waveform of G is determined by the waveform of the heating pulse I_e(t), such as square pulse, sinusoid pulse, Gauss pulse, etc. To be true for all kinds of heating pulses, the expression of G is not restricted in the following formula.

Next, we will give out the pulse decomposition formula and its deduction, based on known N, G, and p⁽ⁱ⁾.

(i) Let

where K = (τ _p/(Nt_s))^round is the nearest integer greater than or equal to the ratio between N and the length of the vibrating part of G, τ _p is the duration of a laser pulse or an electromagnetic wave pulse, t_s is the sampling interval, and the subscript “ round” means taking the round number. Substituting them into Eq. (6) gives

(ii) According to the definition of K, vibration of an acoustic pulse lasts no more than (K− 1) pulses. Thus, a point value in p′ ⁽ⁱ⁾ is actually determined jointly by K pulses emanated from K sector rings, and equation (6) can be rewritten as

where x, y, z are natural numbers.

(iii) According to the order of x in which G_x appears in the sum value , the relationship among x, y, and z is shown as follows:

(iv) Let x = N(k– 1)+ n, where n ∈ [1, N]. This is because the amount of G_x in Eq. (8) is K, and x ≤ KN.

(v) Let z = mN+ n, where m is an integer and m ≥ K. This is because y does not change when z increases from (mN+ 1) to (mN+ N) in Eq. (8).

(vi) According to Eq. (9), we can obtain y = m+ 2– k after giving the exact form of x and z as shown above, and then

where ñ is the positive peak time of G, and is helpful to improve the performance of the pulse decomposition formula when the signal-to-noise ratio (SNR) is low.

(vii) According to Eqs. (6) and (7), equation (10) can be rewritten as

where j = m+ 1– K, and = 0 when j ∈ (− ∞ , 0].

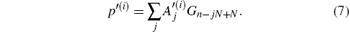
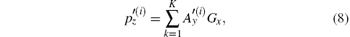
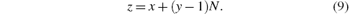
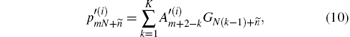
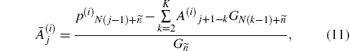
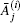
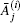
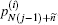
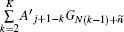
Equation (11) is the formula for dividing an acoustic wave, p⁽ⁱ⁾, into a set of acoustic pulses, g^{(i, j)}, and then obtaining the pulse amplitude as the estimation of . The formula is more accurate than other algorithms only considering one point value such as , because the influences from all acoustic pulses including their negative lobes, as the term , are also taken into consideration in Eq. (11).

4. A new method of reconstructing PAT/TAT image based on pulse decomposition

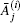
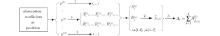After dividing an acoustic wave into a set of acoustic pulses, is measured more accurately, which will be applied to the procedure of image reconstruction for estimating A(r), as shown in Fig. 2. Unlike other techniques such as the TV method, the one with pulse decomposition focuses on the raw signal waveforms and reduces the errors from the source.

Figure Option
View Download New Window

Fig. 2. To measure the absorption coefficient at position r, the new method is composed of three main steps. Step 1: according to Eq. (8), all I acoustic waves are decomposed easily and respectively to obtain the sector ring coefficient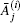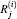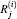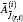

and the position collection

; Step 2: by analyzing

, j̄ _{(r, i)} is easily obtained and means that the position r is located in the j̄ _{(r, i)}-th sector ring for the i-th detector. Step 3: adding

at various i positions together gives an estimation of A_r.

a) In step 1, according to the analysis of the i-th acoustic wave, we can obtain and , where is the collection including all position elements located in the j-th sector ring for the i-th detector, which means that

where denotes the position of the i-th detector.

b) In step 2, can be determined by analyzing or the following equation:

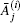
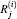
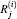
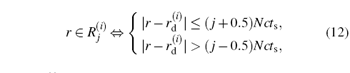
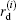
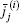
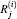
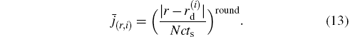
c) According to Eq. (3), just like the basic idea of the DAS algorithm, ^[21] step 3 is to calculate the summation of as the estimation of A(r).

Without changing the DAS algorithm too much, the new reconstruction method can provide a better image in limited-view conditions because of the more accurate estimation of .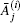

5. Numerical experiment

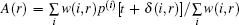
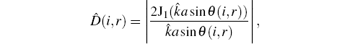
Next, numerical experiments in two dimensions are carried out to prove the new method. A Windows Workstation with an Intel Core i7-2600 3.40 GHz processor having 16 GB memory is used in all computations carried out in this work. For comparison, the weighted DAS method^[21] is employed with the computation equation as , where δ (i, r) is the delay time between the i-th detector and the r-th absorber element, and w(i, r) is the weighting factor representing the receiving sensitivity of the i-th detector to the acoustic signal excited at the position r, which can be measured in practice or calculated by the formula,

where J₁ is the Bessel function, is the wave number, a is the radius of the detector surface, and θ (i, r) is the angle included between the position r and the surface of the i-th detector.

The density ρ = 1000 kg/m³, c = 1500 m/s, and the laser pulse width is 5× 10^{− 8} s. Detectors are placed in an arc with the center at (0, 0) mm, visual angle θ , and the radius 24 mm. The region under test is a square with the center at (0, 0) mm and 30 mm length on a side, and divided into 200 × 200 grids. So the thickness of a sector ring is 0.15 mm. By the way, the thickness should be much less than the size of absorbers, and then it can be adjusted according to the trade off between image fineness and computation cost, which means that increasing the thickness will reduce the computing time but blur the edges of absorbers in the reconstructed image.

There are two kinds of absorbers in the region under test. One kind is a pair of adjacent circles as shown in Fig. 3(a), to measure the performance of reconstruction methods of separating the adjacent absorbers. The circles center at (0, D/2) mm and (0, − D/2) mm respectively, whose radii are both 2 mm. The other kind is a pair of big-small circles as shown in Fig. 4(a), to measure the performance of the reconstruction method of discovering a small absorber with a big one nearby. The big one centers at (7, 0) mm and its radius is 5 mm. The small one centers at (− 5, 0) mm and its radius is R_small.

For the generation of acoustic waves, the sound field is analyzed by the integration method as shown in Eq. (5) and calculated by the differential element method^{[17, 24]} as shown in Eq. (6) through using the COMSOL software. When θ = 75° and D = 8mm, the reconstructed images of adjacent circles by the DAS method and the new method are shown in Figs. 3(b) and 3(c), and the total computational time for them are 2.6637 s and 2.8487 s respectively. Limited-view conditions make phantoms of two circles extend and link together in the DAS image, while there are obvious and confirmative gaps between the two circles in the reconstructed image provided by the new method. It shows that the pulse decomposition is helpful to make a phantom between circles converged into two tiny points and realize separable adjacent absorbers.

When θ = 75° and R_small = 5 mm, the reconstructed images of big-small circles by the DAS method and the new one are shown in Figs. 4(b) and 4(c), and the total computational time for them are 2.6632 s and 2.8511 s respectively. Limited-view conditions make the image of the small absorber almost disappear in the DAS image because of the much higher intensity of the big absorber image, which is still obvious in the image reconstructed by the new method. It shows that pulse decomposition is useful to discover acoustic waves emanated from a small absorber, which is often suppressed by negative lobes of acoustic waves that have emanated from a big absorber.

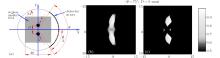	Figure Option View Download New Window
	Fig. 3. (a) Measurement geometry for a pair of adjacent circles; the reconstructed images by (b) the weighted DAS algorithm, and (c) the new method.

	Figure Option View Download New Window
	Fig. 4. (a) Measurement geometry for a pair of big-small circles; the reconstructed images by (b) the weighted DAS algorithm, and (c) the new method.

Next, parametrical experiments are conducted to statistically test the performance of the new method, by sweeping θ of 30° , 35° , 40° , 45° , 50° , 55° , 60° , 65° , and 70° , D of 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 mm, and R_small of 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, and 5.0 mm. Furthermore, a histogram intersection method^[26] is adopted to measure the similarity between the true geometry image and the reconstructed images provided by the DAS and the new method respectively. The histogram intersection is defined as follows:

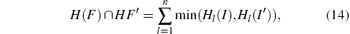
where a color histogram of image F is an L-dimensional vector, H_l(F), in which each element represents the frequency of color l in image F. Additionally, for convenience of data display, the box chart is used to describe the performance of an image reconstructed method with constant θ and varying D or R_small. Statistical parameters corresponding to different parts of a box chart are shown in Fig. 5(c).

We can find the following points. (I) The histogram intersection method is efficient to quantify the image similarity, which shows expected dependence on the view angle. With the increase of θ , the mean values of image similarities increase statistically, no matter whether the reconstruction method is DAS or the new one, the measurement geometry is the adjacent circles or the big-small ones. (II) For the case of the adjacent circles, the mean similarities of the DAS method and the new method vary in the ranges of [0.224 0.226] and [0.295 0.352] respectively. So the new method is about 31% – 58% higher in performance to make two adjacent absorbers separable than the DAS. (III) For the case of the big-small circles, the mean similarities of the DAS method and the new method vary in ranges of [0.224 0.228] and [0.293 0.382] respectively. So the new method is about 31% – 68% higher in performance to discover a small absorber with a big absorber nearby than the DAS.

	Figure Option View Download New Window
	Fig. 5. As an index of imaging quality of the new method (grey boxes) and DAS (empty boxes), similarities between the true geometry image and the reconstructed image, respectively, for the cases of (a) adjacent circles and (b) big-small circles with varying view angles; (c) statistical parameters included in a box chart.

6. Discussion and conclusion

The negative lobe is introduced by the second half of the time derivative of illumination pulses, and represents the shrinkage of absorbers after heat expansion. In conditions of limit-view, it brings obvious errors in estimation of the positive peak values of acoustic pulses, and is one of the main causes of reconstruction distortions. The TV method proves to be a powerful image reconstruction tool in removing background noise, making the image more smooth and preserving edges. Similarly, the idea of pulse decomposition proves to be an effective signal processing tool in analyzing the complicated signals by dividing them into a set of simple pulses. As expected, it shows a good ability to eliminate the negative lobe error and estimate the positive peak values. In this paper, the pulse decomposition formula for PA/TA waves is provided through the detailed deduction, which then forms a new reconstruction method. Numerical experiments prove statically the advantages of the new method over the DAS method, for example, enhancing the imaging quality in conditions of limit-view by more than 30% for the cases of adjacent absorbers and big-small ones.

Reference

View Option

1	Wang L, Xu L S, Feng S T, Meng M Q H and Wang K Q 2013 Comput. Biol. Med. 43 1661 DOI:10.1016/j.compbiomed.2013.08.004 [Cited within:3] [JCR: 1.162]
2	Laurie D P 2011 IEEE Trans. Image Process. 20 361 DOI:10.1109/TIP.2010.2057255 [Cited within:1]
3	Rohwer C H and Laurie D P 2006 SIAM J. Math. Anal. 38 1012 DOI:10.1137/040620862 [Cited within:1] [JCR: 1.573]
4	Suppappola S, Sun Y and Chiaramida S A 1997 Ann. Biomed. Engin. 25 252 DOI:10.1007/BF02648039 [Cited within:2] [JCR: 2.575]
5	Baruch M C, Warburton D E R, Bredin S S D, Cote A, Gerdt D W and Adkins C M 2011 Nonlinear Biomed. Phys. 5 1 DOI:10.1186/1753-4631-5-1 [Cited within:3]
6	Wagner W, Ullrich A, Ducic V, Melzer T and Studnicka N 2006 ISPRS Journal of Pho-togrammetry and Remote Sensing 60 100 DOI:10.1016/j.isprsjprs.2005.12.001 [Cited within:2]
7	Lee A, Bloom E D E and Petrosian V 2000 The Astrophysical Journal Supplement Series 131 1 [Cited within:1]
8	Xu M H and Wang L H 2005 Phys. Rev. E 71 016706 DOI:10.1103/PhysRevE.71.016706 [Cited within:2] [JCR: 2.313]
9	Wang Y W, Xie X Y, Wang X D, Ku G, Gill K L, O'Neal D P, Stoica G and Wang L V 2004 Nano Lett. 4 1689 DOI:10.1021/nl049126a [Cited within:1] [JCR: 13.025]
10	Kuchment P and Kunyansky L 2008 Eur. J. Appl. Math. 19 191 [Cited within:1] [JCR: 1.137]
11	Wang X D, Pang Y J, Ku G, Xie X Y, Stoica G and Wang L V 2003 Nat. Biotechnol. 21 803 DOI:10.1038/nbt839 [Cited within:1] [JCR: 32.438]
12	Wang S H, Tao C and Liu X J 2013 Chin. Phys. B 22 074303 DOI:10.1088/1674-1056/22/7/074303 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
13	Kruger R A, Kiser W L Jr, Reinecke D R and Kruger G A 2003 Med. Phys. 30 856 DOI:10.1118/1.1565340 [Cited within:1] [JCR: 2.911]
14	Wu D, Tao C, Liu X J and Wang X D 2012 Chin. Phys. B 21 014301 DOI:10.1088/1674-1056/21/1/014301 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
15	Yang Y Q, Wang S H, Tao C, Wang X D and Liu X J 2012 Appl. Phys. Lett. 101 034105 DOI:10.1063/1.4736994 [Cited within:1] [JCR: 3.794]
16	Huang L, Rong J, Yao L, Qi W Z, Wu D, Xu J Y and Jiang H B 2013 Chin. Phys. Lett. 30 124301 DOI:10.1088/0256-307X/30/12/124301 [Cited within:3] [JCR: 0.811] [CJCR: 0.4541]
17	Tao C and Liu X J 2010 Opt. Express 18 2760 DOI:10.1364/OE.18.002760 [Cited within:2] [JCR: 3.546]
18	Zhang Y, Wang Y Y and Zhang C 2012 Ultrasonics 52 1046 DOI:10.1016/j.ultras.2012.08.012 [Cited within:2] [JCR: 2.028]
19	Zhang Y, Wang Y Y, Li W, Zhang J Q, Li D and Hu B 2012 Optics and Precision Engineering 20 204 DOI:10.3788/OPE. [Cited within:1] [CJCR: 2.239]
20	Yao L and Jiang H B 2011 Biomed. Opt. Express 2 2649 DOI:10.1364/BOE.2.002649 [Cited within:2] [JCR: 3.176]
21	Klemm M, Craddock I J, Leendertz J A, Preece A and Benjamin R 2008 Int. J. Anten. Propag. 2008 1 [Cited within:3]
22	Lim H B, Nhung N T T, Li E P and Thang N D 2008 IEEE Trans. Biomed. Engin. 55 1697 DOI:10.1109/TBME.2008.919716 [Cited within:1]
23	Paltauf G, Nuster R, Haltmeier M and Burgholzer P 2007 Inverse Problems 23 S81 DOI:10.1088/0266-5611/23/6/S07 [Cited within:1] [JCR: 1.896]
24	Xu M H and Wang L V 2006 Rev. Sci. Instrum. 77 041101 DOI:10.1063/1.2195024 [Cited within:2] [JCR: 1.367]
25	Zwick M and Zeitler E 1973 Optik 38 550 [Cited within:1] [JCR: 0.524]
26	Lee S M, Xin J H and Westland S 2005 Color Research & Application 30 265 DOI:10.1167/14.13.10 [Cited within:1]

2013

1.162

0.0

Wang

, Xu

L S

, Feng

S T

, Meng

M Q H

and Wang

K Q

2013 Comput. Biol. Med. 43 1661 DOI:10.1016/j.compbiomed.2013.08.004

Analysis of pulse waveform is a low cost, non-invasive method for obtaining vital information related to the conditions of the cardiovascular system. In recent years, different Pulse Decomposition Analysis (PDA) methods have been applied to disclose the pathological mechanisms of the pulse waveform. All these methods decompose single-period pulse waveform into a constant number (such as 3, 4 or 5) of individual waves. Furthermore, those methods do not pay much attention to the estimation error of the key points in the pulse waveform. The estimation of human vascular conditions depends on the key points' positions of pulse wave. In this paper, we propose a Multi-Gaussian (MG) model to fit real pulse waveforms using an adaptive number (4 or 5 in our study) of Gaussian waves. The unknown parameters in the MG model are estimated by the Weighted Least Squares (WLS) method and the optimized weight values corresponding to different sampling points are selected by using the Multi-Criteria Decision Making (MCDM) method. Performance of the MG model and the WLS method has been evaluated by fitting 150 real pulse waveforms of five different types. The resulting Normalized Root Mean Square Error (NRMSE) was less than 2.0% and the estimation accuracy for the key points was satisfactory, demonstrating that our proposed method is effective in compressing, synthesizing and analyzing pulse waveforms. (C) 2013 Elsevier Ltd. All rights reserved.

Wang, Lu 1 ;Feng, Shuting 2 ;Xu, Lisheng 2,3 ;Meng, Max Q-H 4 ;Wang, Kuanquan 5 ;

... IntroductionPulse decomposition refers to dividing a synthesized wave into a set of constituent pulses,^{[1#cod#x2013 ...}

... ^[1,5,6] For example, a segment of a typical electrocardiogram (ECG) wave can be decomposed into a sum of several constituent Gaussian pulses with various amplitudes, sharpness, and time positions, which respectively represent working conditions of primary systole, kidney, and ilium, etc ...

... ^[1,5] ...

2011

0.0

... Pulse decomposition has been successfully used in not only ECG signal analysis,^[4,5] but also the study of gamma-ray burst time profiles,^[7] image processing,^[2,3] topographic mapping by airborne lasers,^[6] etc ...

2006

1.573

0.0

1997

2.575

0.0

... 4] and then makes a complex phenomenon understood more easily ...

2011

0.0

Baruch

M C

, Warburton

D E R

, Bredin

S S D

, Cote

, Gerdt

D W

and Adkins

C M

2011 Nonlinear Biomed. Phys. 5 1 DOI:10.1186/1753-4631-5-1

Background Markers of temporal changes in central blood volume are required to non-invasively detect hemorrhage and the onset of hemorrhagic shock. Recent work suggests that pulse pressure may be such a marker. A new approach to tracking blood pressure, and pulse pressure specifically is presented that is based on a new form of pulse pressure wave analysis called Pulse Decomposition Analysis (PDA). The premise of the PDA model is that the peripheral arterial pressure pulse is a superposition of five individual component pressure pulses, the first of which is due to the left ventricular ejection from the heart while the remaining component pressure pulses are reflections and re-reflections that originate from only two reflection sites within the central arteries. The hypothesis examined here is that the PDA parameter T13, the timing delay between the first and third component pulses, correlates with pulse pressure.

1.Empirical Technologies Corporation, PO Box 8175, 3046A Berkmar Drive, Charlottesville, Virginia 22906, USA 2.Cardiovascular Physiology Laboratory, University of British Columbia, 6108 Thunderbird Blvd, Vancouver, British Columbia V6T 1Z3, Canada

... ^[1,5] ...

2006

0.0

2000

0.0

2005

2.313

0.0

... It has proved to have practical potential to draw a clear distinction of contributions made by plenty of constituent pulses, which is also necessary in image reconstruction of photoacoustic tomography (PAT)^{[8#cod#x2013 ...}

... In some image reconstruction methods,^{[8,21#cod#x2013 ...}

2004

13.025

0.0

2008

1.137

0.0

2003

32.438

0.0

2013

1.148

1.2429

Wang

S H

, Tao

and Liu

X J

2013 Chin. Phys. B 22

074303

DOI:10.1088/1674-1056/22/7/074303

Effects of an ultra-strong magnetic field on electron capture rates for Co-55 are analyzed in the nuclear shell model and under the Landau energy levels quantized approximation in the ultra-strong magnetic field, and the electron capture rates on 10 abundant iron group nuclei at the surface of a magnetar are given. The results show that electron capture rates on Co-55 are increased greatly in the ultra-strong magnetic field, by about 3 orders of magnitude generally. These conclusions play an important role in future study of the evolution of magnetars.

Du Jun 1 ;Li Ping-Ping 1 ;Luo Xia 1,2 ;

Effects of ultra-strong magnetic field on electron capture rates for 55 Co are analyzed in the nuclear shell model and under the Landau energy levels quantized approximation in the ultra-strong magnetic field, and the electron capture rates on 10 abundant iron group nuclei at the surface of magnetar are given. The results show that electron capture rates on 55 Co are increased greatly in the ultra-strong magnetic field, by about 3 orders of magnitude generally. These conclusions play an important role in future studying the evolution of magnetar.

... 12] and thermoacoustic tomography (TAT) ...

2003

2.911

0.0

... ^{[13#cod#x2013 ...}

2012

1.148

1.2429

... Actually, limited-view conditions^{[14,16,18#cod#x2013 ...}

2012

3.794

0.0

2013

0.811

0.4541

Huang

, Rong

, Yao

, Qi

W Z

, Wu

, Xu

J Y

and Jiang

H B

2013 Chin. Phys. Lett. 30

124301

DOI:10.1088/0256-307X/30/12/124301

Metal-insulator-semiconductor back contact has been employed for a perovskite organic lead iodide heterojunction solar cell, in which an ultrathin Al2O3 film as an insulating layer was deposited onto the CH3NH3PbI3 by atomic layer deposition technology. The light-to-electricity conversion efficiency of the devices is significantly enhanced from 3.30% to 5.07%. Further the impedance spectrum reveals that this insulating layer sustains part of the positive bias applied in the absorber region close to the back contact and decreases the carrier transport barrier, thus promoting transportation of carriers.

Shi Jiang-Jian 1,2,3 ;Xu Yu-Zhuan 1,2,3 ;Li Chun-Hui 1,2,3 ;Lv Song-Tao 1,2,3 ;Zhu Li-Feng 1,2,3 ;Dong Juan 1,2,3 ;Luo Yan-Hong 1,2,3 ;Li Dong-Mei 1,2,3 ;Meng Qing-Bo 1,2,3 ;Dong Wan 4 ;Chen Qiang 4 ;

... 16] ...

... Actually, limited-view conditions^{[14,16,18#cod#x2013 ...}

... Aiming at this problem, some image reconstruction techniques such as the total variation (TV) method,^{[16,18#cod#x2013 ...}

2010

3.546

0.0

... ^[17] Sometimes, because of wave superposition, negative lobes of an acoustic pulse emanated from a big absorber may entirely suppress a pulse emanated from a small absorber nearby ...

... (5) and calculated by the differential element method^[17,24] as shown in Eq ...

2012

2.028

0.0

... Actually, limited-view conditions^{[14,16,18#cod#x2013 ...}

... Aiming at this problem, some image reconstruction techniques such as the total variation (TV) method,^{[16,18#cod#x2013 ...}

2012

0.0

2.239

Zhang

, Wang

Y Y

, Li

, Zhang

J Q

, Li

and Hu

2012 Optics and Precision Engineering 20 204 DOI:10.3788/OPE.

For insufficient sampling data existing in the practical application of Photoacoustic Tomography (PAT), a reconstruction method based on total variation method was proposed for photoacoustic imaging to solve this problem. The residual between the real signals and the simulated ones from the reconstructed image was calculated for the update image, and the iteration was implemented to obtain the reconstruction image. During the process of iteration, the total variation method in the compressed sensing was utilized to obtain the image with the smallest total variation value by the gradient descent method. Through the numerical simulation, the image reconstruction in the case of insufficient sampling data was accomplished. The results demonstrate that the reconstruction method based on the total variation has better performance as compared with the filtered back-projection method, deconvolution reconstruction method and algebraic reconstruction method. For the 30 sampling points, the peak signal-noise ratio of the reconstructed image is 30.98, 22.09, 8.35 dB higher than those reconstructed by tree kinds of other methods metioned above, respectively. The result of in vitro experiment also shows that this method is more effective for noise suppression.

Department of Electronic Engineering, Fudan University, Shanghai 200433, China

针对光声成像在实际应用中涉及的采样数据不足,提出了一种基于全变分法的光声图像重建方法。通过计算重建图像的模拟信号与实际信号的残差来更新图像,进行迭代以获取重建图像。在迭代重建的过程中引入压缩传感理论中的全变分法,通过梯度下降法得到全变分最小的图像。通过数值仿真,模拟了在不足采样情况下的图像重建。结果表明,全变分重建法的重建效果比滤波反投影法、反卷积重建算法及代数重建算法等3种方法更好。在30个采样点的情况下,重建图像的峰值信噪比值比上述3种算法的重建结果分别高出30.98,22.09和8.35 dB。另外,仿体实验结果也表明该方法能更有效地避免噪声的干扰。

2011

3.176

0.0

... 20] occur quite frequently because of practical constraints due to the imaging hardware, scanning geometry, or ionizing radiation exposure ...

... 20] involved in the compress sensing (CS) theory, are adopted successfully by minimizing TV of reconstructed images iteratively because the image intensity does not change dramatically in most PAT applications ...

2008

0.0

... In some image reconstruction methods,^{[8,21#cod#x2013 ...}

... (3), just like the basic idea of the DAS algorithm,^[21] step 3 is to calculate the summation of as the estimation of A(r) ...

... For comparison, the weighted DAS method^[21] is employed with the computation equation as , where #cod#x03B4 ...

2008

0.0

2007

1.896

0.0

... ^[25] Thus, there may be an obvious difference between and ,^[23] when negative lobes of other acoustic pulses lasting at time t_j have a much greater influence on ...

2006

1.367

0.0

... 24], a point value in the acoustic wave p⁽ⁱ⁾, is selected as the estimation of , and t_j is the positive peak time of g^(i,j) ...

... (5) and calculated by the differential element method^[17,24] as shown in Eq ...

1973

0.524

0.0

... ^[25] Thus, there may be an obvious difference between and ,^[23] when negative lobes of other acoustic pulses lasting at time t_j have a much greater influence on ...

2005

0.0

... Furthermore, a histogram intersection method^[26] is adopted to measure the similarity between the true geometry image and the reconstructed images provided by the DAS and the new method respectively ...