Corresponding author. E-mail: alexander-galashev@yandex.ru
Project supported by the Russian Foundation for Basic Research (Grant No. 13-08-00273).
The process of graphene cleaning of a copper film by bombarding it with Ar13 clusters is investigated by the molecular dynamics method. The kinetic energies of the clusters are 5, 10, 20, and 30 eV and the incident angles are θ = 90°, 75°, 60°, 45°, and 0°. It is obtained that the cluster energy should be in the interval 20 eV–30 eV for effective graphene cleaning. There is no cleaning effect at vertical incidence ( θ = 0°) of Ar13 clusters. The bombardments at 45° and 90° incident angles are the most effective on a moderate and large amount of deposited copper, respectively.
Recently, graphene has attracted considerable interest because of its unique physical properties and energy-band structure. It is now possible to receive graphene of a small size with the help of different technologies. However, a new technology for producing the graphene film of the size up to 70 cm has been developed.[1] Graphene can be used in different membranes due to its high flexibility and mechanical strength. As an absorbing material, graphene is effective only in the case of multiple use. Consequently the question of graphene cleaning of deposited substances arises. In addition, there is a need to develop an effective method for releasing copper from scrap copper– graphene electrodes that have recently been used in electrochemical devices operating in aggressive environments. A graphene coating on copper significantly (by one and half orders of magnitude) increases the resistance of the metal to electrochemical degradation. This copper has a significant practical interest. Surface pollutions on graphene are removed by an ion beam.[2] Bombardment with the cluster beam can be an effective method of graphene cleaning. It is important here, however, to find the correct bombardment energy to avoid causing damage to the graphene membrane. Molecular dynamics (MD) simulation of plasma interaction on a graphite surface has shown that the graphite surface absorbs the most part of hydrogen atoms when the energy of incident beam is 5 eV.[3] At the same time, almost all of the hydrogen atoms are reflected from the surface at a beam energy of 15 eV. Vertical bombardment by Ar10 clusters with kinetic energy Ek < 30
The ion track lithographic method uses the passage of energetic ions through nanoholes in the mask and the subsequent bombing of the graphene sheet only within a limited nanoregion. It is important to investigate in detail the entire lithographic process to predict how nanostructures can be produced in the suspended graphene sheet using this method. The present study will contribute to achieving this goal. The controlled ion parameters obtained in our simulation will be used to obtain desirable defective structures. So far, no experimental studies have been performed to produce such cluster ions to irradiate a target containing graphene. Furthermore, it has been shown that the theory of irradiation effects for bulk targets does not always lead to satisfactory results for low-dimensional materials, such as graphene.[5, 6] It is quite obvious that an atomically thin target of graphene requires explicit consideration of the atomic structure.[7, 8]
The aim of the present work is to investigate the stability of the thin copper film on graphene under Ar13 clusters bombardment with kinetic energies of 5, 10, 20, and 30 eV and incident angles of the cluster beam of 90° , 75° , 60° , 45° , and 0° .
Interatomic interactions in graphene are described in terms of the modified Tersoff many-body potential.[9] The length of the covalent bond is increased to 0.23 nm, and an additional weak attraction at r > 0.23 nm as defined by the Lennard-Jones potential is included.[10] To eliminate the resultant torque at each graphene lattice site, the torsion component of the force generated by the atoms of adjacent sites is excluded.[10] The graphene sheet is placed on a rigid substrate which does not allow C atoms to move vertically downwards. Thereby, the movement of the sheet under the influence of cluster impacts is completely excluded. If atom C has a negative z-coordinate and the vertical component of the velocity vz, then it was assumed that z = 0 and the direction of its total velocity vector υ varied in accordance with the law of elastic collision of the ball against the wall. The boundary conditions at the edges of graphene are free. This allows us to investigate the stability of the edges against external dynamic loads. Atomic interactions in the copper film are modeled by the use of the Sutten– Chen many-body potential.[11] The copper– carbon interaction is described by the Morse potential.[12] In the Ar13 cluster, the atoms are assumed to interact via the Lennard-Jones potential.[13] The interaction between Ar atoms and the target (Cu and C) atoms is determined by the purely repulsive Moliere potential.[14] We neglect the weak attraction between the Ar and Cu atoms on the one hand and the Ar and C atoms on the other hand, since the primary subject of this study is energy and momentum transfer not chemical bonding.[15]
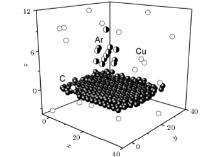
The copper film formation on the graphene is simulated by dividing the MD calculation into two steps. At the first step, Cu atoms are placed over the centers of noncontiguous graphene cells so that the distance between Cu and C atoms would be equal to the distance of 2.243 Å calculated by the density functional theory.[16] Onto this loose film consisting of 49 copper atoms, another 51 Cu atoms were deposited at random. In the initial state the copper film presents a three-dimensional (3D) structure with an ordered lower base (adjacent to the graphene), and an irregular and not flat top layer. The system composed of 100 Cu atoms and 406 C atoms is then equilibrated in the MD calculation over a duration of 1 million time steps (Δ t = 0.2 fs). The equation of motion is solved numerically by the fourth-order Runge– Kutta method. The target obtained in this manner is subsequently bombarded with icosahedral Ar13 clusters during 1 ns.
In the case of vertical bombardment (θ = 0° ) the virtual rectangular two-dimensional (2D) 5 × 5 grid covers the graphene sheet. A virtual grid is lifted over graphene sheet at a distance of 1.5 nm. Every grid node gives the initial position to Ar13 cluster living 8 ps. The lifetime includes time of flight and time of interaction with the target. After this time Ar atoms of decayed cluster are excluded from consideration and a new cluster Ar13 is launched from a different point cluster source. In the case of inclined bombardment, five starting points for placing the centers of the Ar13 clusters are uniformly spaced apart on a line parallel to the oy axis (chair direction). This line is displaced to the left (along the ox axis) from the left edge of the graphene by a distance of 1.5 nm and raised to such a height (in the direction of the oz axis) that it can provide an effective impact on the copper film. An interval equal to the Lx length of the graphene sheet in the axial direction (the direction of zigzag) was divided into 25 equal segments of length Li = Lx/25. Five point cluster sources move horizontally forward by a distance Li at the beginning of each cycle (except for the first), thus the cluster impacts line is moved. As a result, the graphene sheet was covered with 125 evenly spaced points corresponding to target cluster impacts.
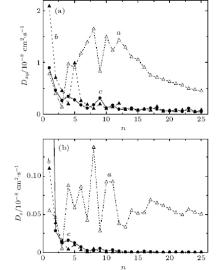
Because of the system geometry, it is necessary to separately investigate the horizontal Dxy and vertical Dz components of the self-diffusion coefficient. Stress calculation in metal film is described in Ref. [11]. Stresses distribution in graphene is obtained by calculating the ratio of the corresponding resultant force acting on a selected site to the area of this site. The surface roughness is calculated as an average arithmetic deviation of the surface profile.
There is no graphene surface cleaning after vertical bombardment at energy 5 eV– 20 eV. Bombardment with 10 eV and 20 eV energies does significant damage to the graphene edges, up to knocking out carbon atoms. The copper film becomes looser and Cu atoms form a column. The graphene sheet is partly clean of copper atoms after bombardment with energy 20 eV at incident angle θ = 75° . The graphene is almost clean of Cu atoms at angles θ = 45° and θ = 60° , separately. In each case, after finishing the inclined bombardment the graphene sheet is removed in the parallel or perpendicular (down) direction with respect to its initial position. This allows us to totally remove copper from the graphene only after bombardment at 45° . In the case of bombardment by the “ nap of the earth” flight method (incident angle 0° ), a large number of metal atoms are still on the graphene surface when the energy of the emitted cluster is 10 eV but the number of copper atoms is reduced at energy 20 eV (Fig. 1).
At any cluster incident angle the mobility of Cu atoms in the horizontal plane is much greater (in the order of magnitude) than in a vertical direction. After the first cycles of cluster impacts there are high values of Dxy components, especially at the incident angle θ = 60° (Fig. 2(a)). This seems reasonable because the copper film has not yet adapted to the bombardment. The more intensive fluctuations and significantly higher Dxy values testify to the continuous fast destruction of copper film during cluster impacts at incident angle 45° . The vertical component Dz of copper film self-diffusion coefficient has almost the same behavior as the Dxy(n) function (Fig. 2(b)).
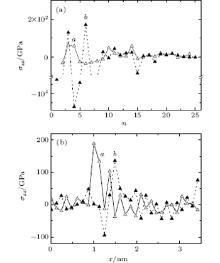
Stress in the xy plane of copper film at each bombardment has an extensive fluctuation, which becomes weaker during the last impact series. At all incident angles, excluding θ = 90° , the σ zz stresses are considerably higher than σ zx and σ zy ones. At θ = 90° and energy of 10 eV the σ zx, σ zy, and σ zz stress components for metal film in horizontal plane have comparably low values during the whole run (Fig. 3(a), where only σ zz is shown). For an energy of 20 eV at the initial target bombardment (n ≤ 10) there are significant fluctuations of all stress components in the horizontal plane. The σ zz component has the most intensive fluctuations. Such fluctuations at energies of bombardment clusters 20 eV and 30 eV are related to the impacts of Ar atoms compressing the film and knocking out the Cu atoms. The fluctuation size of the σ zz value is further reduced because of metal film loosening in a vertical direction.
On the contrary, the stress distribution in the graphene sheet almost does not depend on the direction of the incident cluster beam. Cluster impacts are mainly weakened by the copper film. Stress distributions in graphene between the rows in the “ chair” direction at Ar13 cluster bombardment with energies of 10 eV and 20 eV at θ = 90° are shown in Fig. 3(b). Because of the strong shot-ranged bonds in graphene there are no essential differences between stress values of σ zx, σ zy, and σ zz for a series of cluster bombardments with energies of 10 eV and 20 eV. The σ zx and σ zy stresses are uniformly distributed in the planes of the graphene sheet. For both energies, the maximum σ zz stresses in this area of graphene sheet are 4– 7 times higher than the maximum values of σ zx and σ zy stresses, which is related to the impulses transmitted to graphene from Cu atoms that they obtain due to their interactions with Ar atoms.
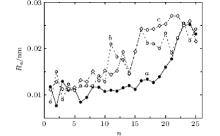
The graphene roughness increases significantly by the end of bombardment. This does not depend on the incident angle or on the energy of the beam of Ar13 clusters. Significant growth of the roughness is limited by the rigid bonds in the graphene. The roughness Ra of the graphene sheet rises non-monotonically during bombardment (Fig. 4). When the clusters energy is 10 eV, the value of Ra slowly increases with low amplitude. There are considerable fluctuations of Ra (n) function, especially in the values range of 10 ≤ n ≤ 25 when energies are 20 eV and 30 eV. The decrease of initial growth of roughness in the case of energy 20 eV is related to the reduction of final Ra value because of the smoothing effect. At the final bombardment step the Ar13 cluster flies rather low over the graphene surface and “ polishes” it, not meeting the Cu atoms.
Incident angle θ = 45° is the most effective for the graphene cleaning of copper by bombardment with argon clusters. Cluster beam energy should be no less than 20 eV. The stresses in the copper film relax rapidly due to its plasticity and a large loss of atoms. Local stresses in graphene relax much more slowly due to the presence of hard bonds and do not disappear even after the bombardment, which indicates its crystalline nature. The presence of local stresses even in thermodynamic equilibrium is a characteristic feature of an ordinary 3D crystal. The instability of 2D crystal against the displacement of atoms in the third dimension is well known and experimentally expressed in a rippled graphene surface. The cluster bombardment of the target greatly enhances this instability and ultimately leads to the surface topography characterized by a large (relative to the value of Ra of the non-bombarded graphene) roughness. To use such a cleaning method it is important to protect the graphene edges because they can be strongly damaged. If it is possible to execute accurate bombardment, then the “ nap of the earth” flight method is the most effective one here. Total cleaning can be obtained with emitted clusters energy of 20 eV and higher. The graphene edges, when using such a cleaning method, are less damaged. While the graphene is being cleaned of copper by argon bombardment, it is possible to obtain copper nanoparticles. Particle size is controlled by the pressure of the formed buffer gas (Ar). Flying out of the copper atoms is inhibited and aggregated as a result of interactions with Ar atoms.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|