Cite this Article
Zhuang Chun-Qiang, Liu Lei. Fluctuations of electrical and mechanical properties of diamond induced by interstitial hydrogen* . Chinese Physics B, 2014, 24(1): 018101  
Permissions
Fluctuations of electrical and mechanical properties of diamond induced by interstitial hydrogen*
Zhuang Chun-Qianga)†, Liu Leib)
Institute of Microstructure and Properties of Advanced Materials, Beijing University of Technology, Beijing 100124, China
Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China

Corresponding author. E-mail: chunqiang.zhuang@bjut.edu.cn

Project supported by the Project of Construction of Innovative Teams and Teacher Career Development for Universities and Colleges under Beijing Municipality, China (Grant No. IDHT20140504), the National Natural Science Foundation of China (Grant No. 51402009), and the Foundation for Young Scholars of Beijing University of Technology, China.

Abstract

While experimental evidence demonstrates that the presence of hydrogen (H) impurities in diamond films plays a significant role in determining their physical properties, the small radius of the H atom makes detecting such impurities quite a challenging task. In the present work, first-principles calculations were employed to provide an insight into the effects of the interstitial hydrogen on the electrical and mechanical properties of diamond crystals at the atomic level. The migrated pathways of the interstitial hydrogen are dictated by energetic considerations. Some new electronic states are formed near the Fermi level. The interstitial hydrogen markedly narrows the bandgap of the diamond and weakens the diamond crystal. The obvious decrement of the critical strain clearly implies the presence of an H-induced embrittlement effect.

Keyword: 81.05.ug; 61.72.jj; 62.20.mj; diamond crystal; impurity effect; density functional theory; brittleness
1. Introduction

During the growth of diamond films by a chemical vapor deposition (CVD) method, the diamond surface is continuously surrounded by abundant energetic hydrocarbon (CHx) species and atomic hydrogen (H).[1– 5] The atomic H tends to passivate the growing surface of the diamond film by forming C– H bonds. The succeeding diamond growth relies on the continuous exchange of the terminating H with the CHx species.[6, 7] However, this equilibrated exchange process may be disturbed by local energy fluctuations on the diamond surface, which results in the entrapment of H atoms in the diamond crystals.[8– 11] Locations where the H atoms may be trapped have not yet been determined. The small radius of the H atom makes it extremely challenging to experimentally detect H impurities in the diamond crystals. It has been experimentally proven that H impurities, which are mainly bounded with crystal defects or bonded to the diamond surface, greatly affect a range of physical properties of the diamond films, including electrical properties.[12– 17] As of yet, the role of H impurities within diamond crystals, particularly interstitial hydrogen, has not been properly identified.

A diamond crystal can be viewed as two interpenetrating face-centred cubic (FCC) lattices, where one is displaced relative to the other along a body diagonal by a one-fourth of the lattice constant. In this arrangement, two types of interstitial sites are generated, which have octahedral and tetrahedral symmetries. According to the volume formula of the pyramid, the corresponding volumes of the two interstitial sites are approximately 6.9  Å 3 and 1.7  Å 3, respectively. The volume of the H atom is only 0.14  Å 3, which is far smaller than that of either interstitial site. Hence an H atom can occupy either of the interstitial sites in a diamond crystal.[18] The previous theoretical studies of the interstitial hydrogen in a diamond have mainly focused on several special positions with a particular symmetry in the interstitial sites.[8, 19, 20] These are known as the center of the tetrahedral site (T site), the body center of the diamond crystal (T site), the bonding center of two neighboring carbon atoms (BC site), the midway vacancy between two T sites (H site), and the midway vacancy between the body center and the face center (C site). However, these positions are only parts of the locations in which an interstitial hydrogen atom may be trapped. Numerous other interstitial positions in the diamond crystal, which may trap H atoms, have not yet been investigated. As previously indicated, a trapped H atom does not remain still in an interstitial site. Given energy fluctuations, [21] H atoms trapped in energetically unfavorable positions are unstable and may overcome potential barriers in the diamond lattice to migrate towards more stable interstitial sites. Such possible migration pathways have not been well experimentally verified. In addition, the migrations of the interstitial hydrogen might potentially affect the mechanical and electrical properties of the diamond films. In this work, we search for the positions of the interstitial sites which may trap H atoms as completely as possible. Furthermore, we study possible migration pathways from unstable positions for the interstitial hydrogen. Based on the findings, the effect of the interstitial hydrogen on the mechanical and electrical properties of the diamond is investigated.

2. H starting positions and computational methods

The diamond crystal structure belongs to the Fd-3m space group (No.  227) (Fig.  1(a)) According to the geometric symmetry, tetrahedral and octahedral interstices in the diamond can be divided into 24 and 16 equal parts, respectively. The site A-ODH in Fig.  1(b) is a representative one of all equivalent octahedral interstices and I-JKE in Fig.  1(c) is that of the tetrahedral ones. Regarding the octahedral site, the various positions which are chosen in A-ODH for the interstitial hydrogen are shown in Fig.  1(b). The interstitial hydrogen in the tetrahedral sites is studied in a similar manner. All these positions can basically represent the possible locations for interstitial hydrogen after exchange and collision processes during the growth of a CVD diamond. Based on the complete relaxation of the diamond lattice without any imposed restrictions, the interstitial hydrogen located at these positions displays diverse migration pathways.

Fig.  1. (a) Locations of octahedral (A-CFED-B) and tetrahedral (G-ADE) interstitial sites in diamond. Carbon atoms are represented by dark grey balls. (b) Starting H positions are represented by light grey balls in one part (A-DOH) of the octahedral interstitial site. (c) Starting H positions are represented by light grey balls in one part (I-JKE) of the tetrahedral interstitial site.

First-principles calculations on an 8-atom diamond unit cell are performed by employing the density functional theory (DFT) and the plane-wave pseudopotential technique as implemented in the CASTEP program.[22, 23] The ion– electron interaction is modeled by norm-conserving pseudopotentials.[24] An energy cutoff of 1000 eV is used for the plane-wave basis to ensure the convergence of the total energy and stress. A generalized gradient approximation (GGA) with the PW91 parameterization is adopted in order to describe the exchange– correlation interaction.[25] An 8× 8× 8 Monkhorst– Pack k-point mesh is employed for the k-point sampling in the Brillouin zone of the reciprocal space after our test on the energy convergence. Convergence tests have been performed on the lattice constant, the mechanical parameters, and the bandgap of the diamond. The corresponding data are listed in Table  1. The excellent agreement between experimental[26– 28] and present theoretical results verifies that the set of parameters can reproduce experimental results quite well.

Table 1. Calculated lattice constant, bulk modulus K, shear modulus G, Young’ s modulus E, bulk modulus to shear modulus ratio, Possion ratio ν , and bandgap of the diamond. Experimental data are also shown for comparison.
3. Results and discussion
3.1. H in octahedral and tetrahedral interstitial sites

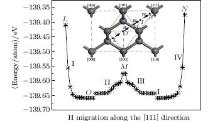
The positions of the interstitial hydrogen in the octahedral interstitial of the diamond (Fig.  1(b)) can be approximately classified into three types: close to the C atoms, close to the body center, and close to the [111] direction of the diamond lattice. In the case that the interstitial hydrogen is close to the C atoms (Fig.  2), it will migrate towards the neighboring bond center site (BC), [8] which is formed by two C atoms in the diamond lattice. In the case that it is close to the body center (Fig.  2), the interstitial hydrogen will migrate towards the body center site, i.e., the center of the octahedral interstitial site. In the case that it is close to the [111] direction (Fig.  3), it will migrate towards the [111] direction. This clearly implies that the migration directions have a close relationship with the starting positions of the interstitial hydrogen. In an attempt to further examine the migrations from other sites, we place an interstitial hydrogen on the positions which were proposed in previous works.[8] The interstitial hydrogen behaves in a similar manner and indeed migrates towards the body center, the bond center, or the [111] direction.

Fig.  2. Two representative starting H positions in the octahedral interstitial site of diamond and their migration trajectories marked by solid circles and squares, respectively. One is located near the C atoms (D point in Fig.  1(b)) of the diamond lattice (solid squares, black), which migrates towards the neighboring bond center (BC); the other is located near the body center (O point in Fig.  1(b)) of the diamond lattice (solid circles, orange) and migrates towards the body center, namely, Td.

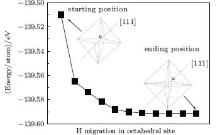Fig.  3. H migration in the octahedral site with the starting H position near the [111] direction and finally it migrates towards the neighboring positions along the [111] direction.

H atoms in the tetrahedral sites are also studied in a manner similar to those in the octahedral ones. Two typical positions close to the center of the tetrahedral interstitials and the C atoms of the diamond lattice are shown in Fig.  4. Similarly, the interstitial hydrogen migrates towards the bond center when it is close to the C atoms of the diamond lattice; otherwise, it migrates towards the center of the tetrahedral interstitial site.

Fig.  4. Two representative starting H positions in the tetrahedral interstitial sites of diamond and their migration trajectories. One is located near the C– C bond in the diamond, which migrates towards the bond center (solid squares, black); the other is located near the body center of the diamond lattice, which migrates towards the center of the tetrahedral interstitial site (solid circle, orange).

3.2. H on positions of [111] direction

As stated above, the interstitial hydrogen migrates towards the neighboring bond center if it is close to the C atoms of the diamond lattice. However, if the interstitial hydrogen is located on positions of the [111] path, it will migrate along the [111] direction either towards the body center or the center of the tetrahedral interstitial site instead of moving towards the neighboring bond center, despite its proximity to the C atoms of the lattice. For such positions, the H migration needs to overcome the energy barriers along the [111] direction. Figure  5 shows the energy distributions along the [111] direction. A small difference in energy exists on the interface of octahedral and tetrahedral interstitial sites (point M in Fig.  5), it is about 0.082  eV/atom as opposed to the much larger 0.28  eV/atom, which is present between the C atoms of the [111] direction and the body center or the center of the tetrahedral sites. Under energy fluctuation conditions which are induced by temperature changes (400– 1700  K), [19, 20] the interstitial hydrogen can overcome such small energy differences and migrate from octahedral to tetrahedral interstitial sites along the [111] direction. When the interstitial hydrogen finally approaches the C atoms on the [111] direction in the tetrahedral interstitial (from pointI to point N in Fig.  5), the increasing energy barrier forces it to bounce back. A similar phenomenon is observed for the interstitial hydrogen in the octahedral interstitial (from point O to point L in Fig.  5). This means that the interstitial hydrogen, which is confined by two C atoms on the [111] axis, shows a tendency to oscillate to and fro between octahedral and tetrahedral interstitials along the [111] direction. Finally, it should be stated that the present work focuses on a prefect diamond crystal. The presence of various other types of defects such as point, line, and planar defects in the diamond crystals impacts the preferred locations of interstitial hydrogen and consequently their migration pathways. Such an effect needs to be studied in depth in future work.

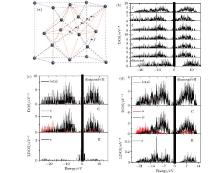
Fig.  5. Energy distributions along the [111] direction between two points L and N. Both points L and N are shown in the inset.

3.3. Electrical properties

The oscillation of the interstitial hydrogen along the [111] direction will surely result in variations of the periodic potentials in the diamond, which will affect the electronic properties of the diamond. Figure  6(a) shows some specific positions on the [111] direction for electronic structure calculations, while figure  6(b) shows the corresponding calculated densities of state (DOS) of the diamond. A bandgap is clearly shown in the pure diamond. However, some new states near the Fermi level do appear when the interstitial hydrogen is introduced into the diamond, which leads to a shift of the conductive edge of the diamond towards the Fermi level. The bandgap is obviously narrowed. The calculated bandgap of the pure diamond is approximately 4.9  eV, while that of the H-containing diamond almost disappears, which highlights the significant influence of the interstitial hydrogen on the electrical properties of the diamond.

Fig.  6. Fluctuations of electrical properties of diamond induced by the interstitial hydrogen along the [111] direction. The same Gaussian broadening with a width of about 0.01 eV is used for all the DOS and LDOS. (a) Specified positions on the [111] direction (pointsa– e). (b) Density of states for H-containing diamond with H atoms at positions a– e. The DOS of pure diamond is also shown for comparison. (c) Local density of states (LDOS) and DOS of H-contained diamond with H atom at the body center of the diamond (point a in panel (a)). (d) LDOS and DOS of H-contained diamond with an H atom at the bond center (point f in panel (a)).

Two representative cases, i.e., the interstitial hydrogen at the body center (point a in Fig.  6(a)) and that at the bond center (point f in Fig.  6(a)), are chosen to verify the detailed effect on the DOS of the diamond. Figure  6(c) shows the total density of states (TDOS) and the local density of states (LDOS) for the interstitial hydrogen at the body center site. For the TDOS, the densities of states below the valence band and above the conduction band are mainly derived from the C atoms of the diamond lattice. The contribution of the interstitial hydrogen to the TDOS is concentrated near the Fermi level, which is probably the reason for the bandgap reduction. On the contrary, the TDOS and the LDOS for the interstitial hydrogen at the bond center, which are shown in Fig.  6(d), are very different from those shown in Fig.  6(c). The contribution of the interstitial hydrogen to the TDOS is mainly concentrated below the valence band and above the conduction band.

3.4. Mechanical properties

In addition to the electrical properties, the mechanical properties of the diamond are also studied. The positions of the interstitial hydrogen considered in the calculations are the same as those in Fig.  6(a). By employing the elastic constants (Fig.  7(a)) which are calculated by first-principles calculations, the bulk (K), the shear (G), and the Young’ s moduli (E) are calculated using the Reuss– Voigt– Hill average.[29] The results are shown in Fig.  7(b). The obtained K, G, and E for the pure diamond are 445  GPa, 544  GPa, and 1159  GPa, respectively. However, when the interstitial hydrogen is introduced into the diamond, the corresponding moduli decrease significantly by about 9.7, % , 32.9% , and 27.5% , respectively. The moduli of the diamond with H at different positions show small variations except for in position e of the tetrahedral interstitial site, which show markedly lower values. Upon a careful examination of the relevant structure, we find that the lattice constant increases by 3.3% and the corresponding C– C bond around the interstitial hydrogen becomes elongated by 1.9% as opposed to those in the pure diamond. This may reduce the bonding strength, weaken the resistance of the diamond to external compression, and consequently decrease the elastic moduli.

Fig.  7. (a) Elastic constants (C11, C12, and C44) at the specified positions a– e. (b) Fluctuations of bulk modulus K, shear modulus G, and Young’ s modulus E of diamond along the [111] direction. The corresponding values are calculated from the elastic constants using the Reuss– Voigt– Hill average.[29] Specified positions a– e are the same as those shown in Fig.  6(a).

In addition to the elastic moduli, the ideal strength is another important description of a material’ s mechanical properties. It has been demonstrated that the failure of a diamond by fracture is mainly dictated by its tensile strength along the [111] direction.[30, 31] Correspondingly, interstitial hydrogen prefers to stay in some positions (e.g., octahedral and tetrahedral sites) in this direction, as stated above, which has a pronounced effect on the ideal strength of the diamond. Figure  8 shows the stress– strain curve in the case when the interstitial hydrogen is located at the body center of the diamond. The tensile strength for the pure diamond is about 90.2  GPa, which is in excellent agreement with a previously calculated value of 92.8  GPa at a 13% strain.[22] However, when the interstitial hydrogen is introduced into the body center of the diamond, the corresponding tensile strength decreases dramatically to a value of about 33 GPa. Furthermore, the critical strain decreases from 13% for the pure diamond to 4% for an H-containing one. It can, therefore, be inferred that the highest achievable tensile strength of the diamond is reduced due to the increasing crystal brittleness caused by the interstitial hydrogen.

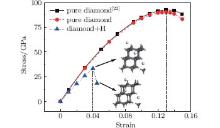Fig.  8. Stress– strain curves for pure diamond and H-contained diamond with the interstitial hydrogen at the body center. The calculated stress– strain curves of pure diamond obtained in Ref. [22] is also shown for comparison.

4. Conclusion

First-principles calculations were employed to study the positions of the interstitial hydrogen in a diamond and its migration pathways. Migration directions are strongly related to the positions of the interstitial hydrogen. If the H position is close to the C atoms of the diamond lattice, the interstitial hydrogen will migrate towards the neighboring bond center, whereas if the H position is close to the [111] direction, it will migrate towards the energy minima of the [111] axis. On the other hand, if the H position is located on some points along the [111] direction, it will still migrate towards the body center or the center of the tetrahedral sites rather than the neighboring bond center, despite its proximity to the C atoms of the [111] direction. In the case that the interstitial hydrogen is located in some positions of the [111] direction, it shows a tendency to oscillate to and fro between the two C atoms on the [111] direction in the octahedral and tetrahedral interstitial sites.

The interstitial hydrogen has an obvious influence on the electrical and mechanical properties of a diamond. The formation of some new states which appear near the Fermi level is induced by the interstitial hydrogen. These promote the conductive edge of the diamond to move towards the Fermi level, and consequently narrow the bandgap. The DOS of the diamond shows a metal-like feature. The interstitial hydrogen greatly weakens the diamond crystal by reducing the bulk, shear, and Young’ s moduli. Introducing the interstitial hydrogen greatly reduces the tensile strength of the diamond. The obvious decrement of the critical strain clearly indicates the presence of an H-induced embrittlement effect.

Acknowledgment

We thank H. Abu Samra for the helpful discussion.

Reference
1 Lee S T, Lin Z and Jiang X 1999 Mater. Sci. Eng. R 25 123 DOI:10.1016/S0927-796X(99)00003-0 [Cited within:1]
2 Zhu X, Hu M, Zhan R, Wen X and Zhou H 1998 Phys. Plasma 5 1541 DOI:10.1063/1.872812 [Cited within:1] [JCR: 2.376]
3 Zhang Z F, Jia X P, Liu X B, Hu M H, Li Y, Yan B M and Ma H A 2012 Chin. Phys. B 21 038103 DOI:10.1088/1674-1056/21/3/038103 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
4 Liu X B, Jia X P, Zhang Z F, Huang H L, Zhou Z X and Ma H A 2011 Chin. Phys. B 20 128102 DOI:10.1088/1674-1056/20/12/128102 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
5 Huang G F, Jia X P, Li S S, Zhang Y F, Li Y, Zhao M and Ma H A 2010 Chin. Phys. B 19 118101 DOI:10.1088/1674-1056/19/11/118101 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
6 Klein-Douwel R J H and ter Meulen J J 1998 J. Appl. Phys. 83 4734 DOI:10.1063/1.367262 [Cited within:1] [JCR: 0.71]
7 Yan B M, Jia X B, Qin J M, Sun S S, Zhou Z X, Fan C and Ma H A 2014 Acta Phys. Sin. 63 048101(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
8 Jonathan P G 2003 J. Phys. : Conden. Mater. 15R551 DOI:10.1088/0953-8984/15/17/201 [Cited within:4]
9 Zhou X, Watkins G D, McNamara Rutledge K M, Messmer R P and Chawla S 1996 Phys. Rev. B 54 7881 DOI:10.1103/PhysRevB.54.7881 [Cited within:1]
10 Jiang X and Jia C L 2002 Appl. Phys. Lett. 80 2269 DOI:10.1063/1.1458071 [Cited within:1] [JCR: 3.794]
11 Gu L P, Tang C L, Jiang X F and Pinto J L 2011 Chin. Phys. B 20 058104 DOI:10.1088/1674-1056/20/5/058104 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
12 Hayashi K, Yamanaka S, Okushi H and Kajimura K 1996 Appl. Phys. Lett. 68 376 DOI:10.1063/1.116690 [Cited within:1] [JCR: 3.794]
13 Hayashi K, Yamanaka S, Watanabe H, Sekiguchi T, Okushi and Kajimura K 1997 J. Appl. Phys. 81 744 DOI:10.1063/1.364299 [Cited within:1] [JCR: 0.71]
14 Hu X J, Ye J S, Zheng G Q, Cao H Z and Tan H C 2006 Chin. Phys. B 15 2170 DOI:10.1088/1009-1963/15/9/044 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
15 Gu C Z, Wang Q, Li J J and Xia K 2013 Chin. Phys. B 22 098107 DOI:10.1088/1674-1056/22/09/098107 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
16 Liu F B, Wang J D, Chen D R and Yan D Y 2009 Chin. Phys. B 18 2041 DOI:10.1088/1674-1056/18/5/052 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
17 Zhang Z Y, Lu X C and Luo J B 2007 Chin. Phys. B 16 3790 DOI:10.1088/1009-1963/16/12/039 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
18 Glover C, Newton M E, Martineau P M, Quinn S and Twitchen D J 2004 Phys. Rev. Lett. 92 135502 DOI:10.1103/PhysRevLett.92.135502 [Cited within:1] [JCR: 7.943]
19 Saada D, Adler J and Kalish R 2000 Phys. Rev. B 61 10711 DOI:10.1103/PhysRevB.61.10711 [Cited within:2]
20 Herrero C P, Ramirez R and Hernand ez E R 2006 Phys. Rev. B 73 245211 DOI:10.1103/PhysRevB.73.245211 [Cited within:2]
21 Goss J P, Eyre R J and Briddon P R 2008 Phys. Status Solidi B 245 1679 DOI:10.1002/pssb.v245:9 [Cited within:1] [JCR: 1.489]
22 Payne M C, Teter M P, Allan D C, Arias T A and Joannopoulos J D 1992 Rev. Mod. Phys. 64 1045 DOI:10.1103/RevModPhys.64.1045 [Cited within:2] [JCR: 44.982]
23 Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J and Payne M C 2002 J. Phys. : Conden. Mater. 14 2717 DOI:10.1088/0953-8984/14/11/301 [Cited within:1]
24 Hamann D R, Schluter M and Chiang C 1979 Phys. Rev. Lett. 43 1494 DOI:10.1103/PhysRevLett.43.1494 [Cited within:1] [JCR: 7.943]
25 Perdew J P and Wang Y 1992 Phys. Rev. B 45 13244 DOI:10.1103/PhysRevB.45.13244 [Cited within:1]
26 Lambrecht W R L and Segall B 1993 Phys. Rev. B 47 9289 DOI:10.1103/PhysRevB.47.9289 [Cited within:1]
27 Grimsditch M, Zouboulis E S and Polian A 1994 J. Appl. Phys. 76 832 DOI:10.1063/1.357757 [Cited within:1] [JCR: 0.71]
28 Knittle E, Kaner R B, Jeanloz R and Cohen M L 1995 Phys. Rev. B 51 12149 DOI:10.1103/PhysRevB.51.12149 [Cited within:1]
29 Hill R 1952 Proc. Phys. Soc. 65 349 DOI:10.1088/0370-1298/65/5/307 [Cited within:1]
30 Telling R H, Pickard C J, Payne M C and Field J E 2000 Phys. Rev. Lett. 84 5160 DOI:10.1103/PhysRevLett.84.5160 [Cited within:1] [JCR: 7.943]
31 Zhang Y, Sun H and Chen C 2004 Phys. Rev. Lett. 93 195504 DOI:10.1103/PhysRevLett.93.195504 [Cited within:1] [JCR: 7.943]