Various mechanisms have been developed to package DNA with much longer dimension compared to its diameter during evolution. In vivo, DNA is organized into a compact structure, a process called DNA condensation. In cells, DNA condensation is mainly achieved by DNA architectural proteins such as histones in eukaryotic cells.^{[1– 3]} In sperms, DNA condensation is accomplished by another important mechanism of spermidine-mediated DNA condensation.^{[4, 5]}In vitro, multivalent cation-mediated DNA condensation has been extensively studied not only because it plays a significant biological role but also because it is an important issue in polymer physics.^{[6– 16]}

Previous electron microscope imaging experiments have suggested that multivalent cations organize DNA into toroid structures.^[6] In the past 20 years, DNA toroid formation has been the focus of much attention, and single-molecule experiments, including optical tweezers and magnetic tweezers experiments, have been carried out to investigate the dynamics of DNA condensation. These powerful tools provided details of step-wise behavior during DNA condensation and measured kinetic characteristics of DNA condensation to provide data beyond the information obtained by classical bulk experiments.

Toroid formation has been considered as a canonical form of DNA condensation because of its regularity and simplicity. Most previous theoretical modelings have been based on an assumption of helical toroidal formation during DNA condensation, wherein the DNA toroid follows a simple circular helical path. On the basis of the circular wrapping model, the free energy landscape of wrapping or unwrapping of one DNA round on the toroid has been analytically derived and has revealed that a large kinetic energy barrier separates the wrapped and unwrapped states and controls the kinetics of DNA condensation and de-condensation.^[7] It predicts stepwise extension changes during DNA wrapping and unwrapping, which were observed in recent single-DNA manipulation experiments.^{[8, 9]}

Although much work has been performed on DNA condensation, the de-condensation process of DNA condensate has not been investigated and the dynamics of this reverse process are not well understood. In this study, DNA de-condensation was carried out using a combination of magnetic tweezers experiments and Brownian dynamics (BD) simulations.

As per the procedure reported in our previous study, ^{[15– 17]} a 10-kbp DNA labeled with biotin and digoxin at each end was anchored to a coverslip surface and a super parallel magnetic M280 bead, respectively, in phosphate buffer (10-mM phosphate, pH 7.5), as shown in Fig. 1(a). First, the condensation process was recorded at 2 pN at the low concentration of 0.2-mM cobalt hexamine in phosphate buffer (Fig. 1(b)). Step-wise condensation behavior was clearly seen, which is consistent with previous experiment results.^{[6, 12, 15]}

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Setup of magnetic tweezers (not to scale). (b) Stepwise dynamics of DNA condensation in the presence of 0.2-mM cobalt hexamine.

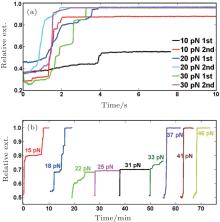
To investigate the dynamics of de-condensation of the DNA condensate formed, a high force (> 10 pN) was applied after the DNA condensed to approximately 30% of the contour length at a low force of 2 pN. After complete unfolding, the same procedure was repeated to investigate the diversity of the unfolding behaviors and the effects of the level of the unfolding forces. Figure 2(a) shows that, in 0.2-mM cobalt hexamine, the DNA condensates can be easily unfolded at forces above 20 pN within several seconds. However, at the same unfolding force, the unfolding speeds and, more importantly, the unfolding steps vary between experiments, indicating the formation of very diverse types of DNA condensates.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (a) Unfolding time traces obtained from experimental folding and unfolding cycles of a DNA molecule in the presence of 0.2-mM cobalt hexamine wherein the condensates could be completely unfolded at 10 pN– 30 pN. (b) In the presence of 2-mM cobalt hexamine, a folded DNA molecule was stretched at different forces. At 15 pN– 18 pN, complete unfolding was observed. At 22 pN– 33 pN, the DNA was locked in a shorter conformation. Complete unfolding occurred at > 33 pN.

It has been revealed that a higher cobalt hexamine concentration could enhance the adhesion force between DNA and could significantly stabilize DNA condensates. To determine the effect of large adhesion force on the DNA de-condensation process, we increased the concentration of cobalt hexamine to 2 mM and repeated the measurement. As shown in Fig. 2(b), DNA condensates could withstand much larger forces and demonstrated complex dependence of unfolding speeds on force. Figure 2(b) shows the results obtained in one experiment where the condensates could be fully unfolded at 17 pN– 18 pN within several minutes but could not be completely unfolded at higher forces at 20 pN– 30 pN for more than 30 minutes, indicating a mechanical stable condensate. At F > 35 pN, rapid unfolding of the condensates occurred.

In 2003, L-selectin:PSGL-1 bonds were found to exhibit an increase in bond lifetime when a force between 0 pN and 25 pN was applied.^[18] At the same time, a similar mechanism was reported in the field of ligand-receptor interactions, ^{[19, 20]} which describes an anti-intuitive phenomenon, that is, an increase in force sometimes slows down the unfolding rate presumably due to force-dependent deformation of the folded proteins. In this study, complex non-monotonic dependence on force and similar catch-bond behavior was revealed in our magnetic tweezers experiments under high adhesion conditions for the DNA condensates.

In single-DNA experiments, besides recording DNA wrapping at low forces, the condensed DNA can also be unwrapped by applying a high force. Previous studies have treated the unwrapping process as a simple reverse process of wrapping from a regular helical spool.^{[6, 12, 15]} This treatment has several potential problems. In previous experiments including our own experiments, we often found that some folded DNA could not be completely unwrapped at forces significantly higher than the critical forces predicted by the spool model in the experimental timescale. This led to questions regarding whether there is a deeper physical mechanism governing the unfolding kinetics.

Brownian dynamics simulation was performed to gain detailed insights into the de-condensation processes of DNA condensates. In the BD simulations, DNA is modeled as a chain of 600 beads with a diameter of d = 2 nm. It can also be viewed as a discredited chain with 599 segments, with the i-th segment connecting the i and i + 1 beads. A segment i has a length of l ∼ l₀ nm, associated with a stretching energy . Here, l₀ = 2 nm was chosen to be the center-to-center distance of the i and i + 1 beads. The stretch modulus of the DNA is κ = f₀/d with f₀ = 1, 500 pN and the bending persistence related to the bending energy of DNA chain is A = 50 nm.^{[21, 22]} A Morse potential is introduced between any two beads in the DNA chain with equilibrium distance at l₀ = 2 nm: U_{i, j} = ε [e^{− 2α (d_{i, j}− l₀)} − 2e^{− α (d_{i, j}− l₀)}], where d_{i, j} is the distance between bead i and another bead j and ε describes the strength of interaction. α ^{− 1} defines a characteristic distance, above which the inter-bead interaction is negligible (i.e., electrostatic screening). A fixed value α = 4 nm^{− 1} is chosen corresponding to a screening length of 0.25 nm.

The total energy U of a given conformation includes the stretching, bending energy and the attractive potential between two beads, which depend on the spatial positions of the beads r_i. The force exerted on a bead is f_i = − ∇ _riU. In a time step Δ t, the new position of bead i can be achieved according to

where ξ = 3π η d is the translational drag coefficient and η = 10^{− 3} Pa· s is the viscosity of water at room temperature. δ r_i is the random spatial displacement accounting for bead diffusion within the time step Δ t, which is Gaussian distribution with a variance of ⟨ δ r_i⟩ ² = 6DΔ t. Here, D is the translational diffusion coefficient which is related to the drag coefficient through the Einstein relation: D = k_BT/ξ . To ensure that the system can reach thermal equilibrium, the time step Δ t chosen should be long enough to allow the diffusion of beads to take place and short enough to ensure that the bead will not be over-displaced during Δ t. In the simulations, a fixed time step of 0.1 ns was used throughout the simulations, which allowed the system to reach equilibrium indicated by 0.5k_BT equally distributed to each degree of freedom of motion.

Figure 3(a) shows DNA conformations during unwrapping on applying two different forces of 40 pN (top panel) and 60 pN (bottom panel) from the same initial folded structure under an adhesion energy density of 1.5k_BT/nm. This is a relatively larger adhesion energy density compared to normal experimental conditions with a typical value around 1.0k_BT/nm.^[7] Clearly, at these two different forces, the DNA toroid undergoes different conformational changes during unwrapping. At the higher force of 60 pN, at each unwrapped stage, the toroid looks flatter than those under 40 pN, which can be easily understood since the toroid is expected to deform more at a higher force than at a lower force. This result signifies that unwrapping at different forces actually undergoes different unfolding pathways, which cannot be considered similar to unwrapping from a rigid body such as a regular helical spool structure.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (a) DNA conformations under 40 pN (top panel) and 60 pN (bottom panel) with an adhesion energy density of 1.5kBT/nm. (b) Unfolding trajectories under six different forces. (c) Average rate of change in extension as a function of the unwrapping force. The catch-bond behavior is seen because of the deformed DNA toroid. (d) and (e) At a low adhesive energy density of 0.75kBT/nm, the rate of unwrapping becomes monotonically dependent on the unwrapping force, and the catch-bond behavior is no longer observed.

As demonstrated in Fig. 3(a), the mechanical unfolding pathway may depend on the force. Therefore, the rate of unwrapping may have a complex dependence on force. It is well known that, in shear force geometry, a folded molecule can withstand large mechanical force. A famous example is that it takes approximately 60 pN of shear force (tension along DNA backbone) to melt dsDNA, whereas it only takes approximately 15 pN to unzip dsDNA.^{[21, 22]} Therefore, a flatter toroid conformation that is closer to the shear force geometry favored at a higher force may be more mechanically stable than the same toroid placed under a lower force. This predicts a possible non-monotonous relation between the unwrapping rate at the unwrapping force. This prediction is tested by simulating unfolding from the same initial structure at the same adhesion energy density of 1.5k_BT/nm at different forces. Figure 3(b) shows that the unfolding trajectories of DNA extension change at six different forces in the range of 30 pN– 80 pN and figure 3(c) shows the average rate of change in extension as a function of the unwrapping force, which was calculated by the change in extension at 20-ms divided by the time. These findings show that the rate of unwrapping has a complex dependence on force and that the dependence is indeed not monotonous.

The above simulations were carried out at a large adhesion strength (i.e., adhesion energy per distance) of ∼ 1.5k_BT/nm. At a lower adhesion energy where DNA is not so tightly adsorbed onto the toroid, we anticipate that DNA can be more easily unwrapped which should reduce the level of deformation of the toroid under tension. This is because the rate of peeling DNA off the toroid increases, which should reduce the time allowed for the toroid to be deformed into the shear force geometry. In such situations, the possibility of catch-bond-like unfolding kinetics should decrease. To test this, we performed a similar simulation with the same initial structure but at a lower adhesion energy density of 0.75k_BT/nm. Indeed, as shown in Fig. 3(d) and 3(e) the rate of unwrapping becomes monotonically dependent on the unwrapping force, and the catch-bond behavior is no longer observed.

Complex dependence of the unfolding rate on force was detected in both simulations and single-DNA manipulation experiments. This dependence is caused not only by the complex topological states of the condensates but also by the force-dependent deformation of the condensates. The results suggest that the condensate cannot be approximated as a rigid body. Under different forces during DNA de-condensation, the condensates may take different conformations resulting in differing mechanical stabilities. As a result, non-monotonic dependence of the unfolding rate of the same condensate on force could occur, as suggested by both simulations and experiments. To the best of our knowledge, such catch-bond behavior has not been previously reported in mechanical unfolding of DNA condensates.