†Corresponding author. E-mail: lfzhu@ustc.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. U1332204, 11274291, 11504361, and 11320101003).
The electron energy loss spectrum of the 4d excitations of xenon was measured at an incident electron energy of 1500 eV and a scattering angle of 6°. Besides the optically allowed transitions of
The energy level structures of atoms and molecules are of great importance from the viewpoints of both the fundamental researches and the applications. The inner-shell excitations of atoms and molecules have been paid special attention since the investigations about them reveal abundant physical information such as the electron correlation and exchange effects, the interference effect between the direct ionization, autoionization and fluorescence de-excitation processes, as well as the decay mechanism of the participator or spectator Auger process.[1– 5] Furthermore, the inner-shell excitations of atoms and molecules, especially those of the noble gases and nitrogen, have been used to test and calibrate the monochromator used in synchrotron radiation.[6– 8] Although nowadays the energy level structures of the valence-shell excitations of atoms and molecules have been well studied and summarized, the knowledge of their inner-shell excitations is relatively scarce. The reason may be due to the fact that the high excitation energy of the inner-shell state is difficult to achieve by the traditional light source and laser. The early investigations about the inner-shell excitations of atoms and molecules were carried out by the high-energy electron energy loss spectroscopy (EELS)[9– 11] and the synchrotron radiation, [12– 18] and recently most works were made by the synchrotron radiation with its dramatic progress.[19– 22] However, only the dipole-allowed transitions are achieved by the synchrotron radiation and the EELS operated at the optical limit, i.e., the momentum transfer is near zero at a scattering angle of 0° which is the most used condition in previous investigations.[9, 10] So the abundant dipole-forbidden inner-shell excitations have seldom been explored experimentally, [23– 27] and this is the main purpose of this work.
As for xenon, its inner-shell excitations were investigated by the synchrotron radiation[12– 14, 18– 21] and high-energy EELS[9, 28] experimentally. More specifically, the experimental energy level positions and the natural widths for the dipole-allowed 4d excitations have been reported by Refs. [9], [18], [19], and [21]. Although the energy positions of the 4d excitations reported by different groups[9, 18] are in good agreement, the experimental natural widths show large discrepancies. The natural widths of the 4d− 1np excitations determined by King et al.[9] show a slight tendency of increase with the principal quantum number n, while the results of Masui et al.[21] are nearly constant and their results are generally lower than others. However, the more recent work of Sairanen et al.[19] gives a slight tendency of decrease in natural widths with the higher n for the resonances in both series of 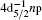
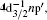


In this paper, the dipole-forbidden excitations of the 4d electron of xenon are studied by the electron impact method with a large momentum transfer, and new information of 4d− 1ns and 4d− 1nd is reported.
In this work, the angle-resolved electron energy loss spectrometer, which has been described in detail in our previous works, [29, 30] was used. In the present experiment, the spectrometer was operated at an incident electron energy of 1.5 keV and a scattering angle of 6° , which corresponds to a squared momentum transfer of 1.20 a.u. (atomic unit). The electron energy loss spectra in the energy regions of 7 eV– 9 eV and 62 eV– 70 eV were recorded simultaneously at a sample pressure of 8.2× 10− 3 Pa. The energy resolution and the instrumental function of the spectrometer were determined from the observed peak of 5p56s[3/2]1 in 7 eV– 9 eV because of its negligible natural width, and the former is 90 meV. The instrumental function of the spectrometer is used to deconvolve the peak profiles of the inner-shell excitations of the 4d electron in 62 eV– 70 eV which will be described below. The measured spectrum is shown in Fig. 1, and the features are assigned according to our calculation (see Table 1) and the previous investigations.[9]
| Table 1. The energies, intermediate-coupling coefficients and the assignments for the peaks from A to L as shown in Fig. 1. Some weak transitions are not included for clarity. The energy levels from our calculations and this experiment are given. E0, E1, E2, and E3 represent the electric monopole, electric dipole, electric quadrupole, and electric octupole transitions from the ground state, respectively. The terms whose intermediate-coupling coefficients are less than 0.2 are neglected. |
The measured spectrum shown in Fig. 1 is the one of the real spectrum convoluted by the instrumental function, and the least-squares fitting was used to determine the line profile parameters such as the energy positions and natural widths of the inner-shell transitions. The fitting function for a peak is expressed as follows:

where
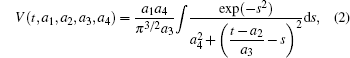

Here the Voigt function V(t, a1, a2, a3, a4) is used to describe the instrumental function, and L(x − t, b1, b2, b3) is the Lorentz function. a1, a2, a3, a4, b1, b2, and b3 are all fitting parameters. As mentioned above, the instrumental function V(t, a1, a2, a3, a4) was determined by fitting the peak of 5p56s[3/2]1. It is believed that the Lorentz function can represent the true line profiles of inner-shell excitations of xenon, since the peak is almost symmetric as shown in Fig. 1 which means that the interaction between the discrete excitation and the ionization continuum is negligible. The same assumption has been used in all previous investigations.[19– 21] Then a function obtained by convolving the instrumental function with a Lorentz function whose central position and line width are variable is used to fit the inner-shell excitations, and the fitted results are also shown in Fig. 1.
In order to assign the measured features shown in Fig. 1, especially for the dipole-forbidden ones, the Cowan code[31] was used to calculate the excitation energies and the intermediate coupling coefficients of the 4d excitations. The method of the calculation was described in detail by Clark et al.[32, 33] and summarized briefly in our recent work.[27, 34] For the present calculations a 26-configuration basis set was used, and the calculated excitation energies as well as the intermediate coupling coefficients are listed in Table 1. In the calculation, the interaction between the discrete state and the ionization continuum was ignored. In addition, the JL designation was adopted.
From Fig. 1, it can be seen that at the scattering angle of 6° , not only the optically allowed transitions of 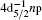
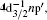
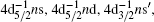

| Table 2. Natural widths of Xe-4d excitations (the numbers in parentheses are standard errors with the units of meV). |
Firstly, we concentrate on the dipole-allowed transitions of 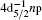
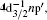





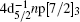
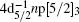




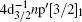




Since the accurate energy level positions of the dipole-allowed transitions have been determined by the previous EELS works[9] and synchrotron radiation ones, [18] as well as the energy resolution of 90 meV in this work is slightly worse than the previous ones, in the least-squares fitting procedure the energy positions of the dipole-allowed excitations were fixed on the ones reported by King et al.[9] Considering the heavy overlapping of the transitions above 64 eV, fixing the energy positions of the dipole-allowed transitions can reduce the fitting errors of the natural widths of these transitions and the parameters of other dipole-forbidden ones.
It can be seen from Table 2 that the best agreement of the natural widths measured by different groups is achieved for the 
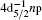
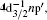









Besides the dipole-allowed transitions mentioned above, abundant dipole-forbidden ones, which are absent in the previous experimental studies, are also observed in the measured spectrum as shown in Fig. 1. The energy position and natural width of the quadrupole transition of 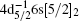
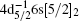
The quadrupole transition of 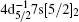
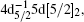
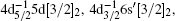
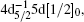
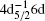

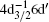


The electron energy loss spectrum of 4d excitations of xenon has been measured at an incident electron energy of 1500 eV and a scattering angle of 6° . Not only the optically allowed transitions of 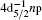
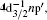
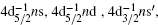

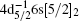
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|





