†Corresponding author. E-mail: yingjiezhang@mail.qfnu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61178012 and 11304179), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant Nos. 20123705120002 and 20133705110001), the Natural Science Foundation of Shandong Province of China (Grant No. ZR2014AP009), and the Scientific Research Foundation of Qufu Normal University.
The lower bounds of the evolution time between two distinguishable states of a system, defined as quantum speed limit time, can characterize the maximal speed of quantum computers and communication channels. We study the quantum speed limit time between the composite quantum states and their target states in the presence of nondissipative decoherence. For the initial states with maximally mixed marginals, we obtain the exact expressions of the quantum speed limit time which mainly depend on the parameters of the initial states and the decoherence channels. Furthermore, by calculating the quantum speed limit time for the time-dependent states started from a class of initial states, we discover that the quantum speed limit time gradually decreases in time, and the decay rate of the quantum speed limit time would show a sudden change at a certain critical time. Interestingly, at the same critical time, the composite system dynamics would exhibit a sudden transition from classical decoherence to quantum decoherence.
Quantum mechanics establishes the fundamental bounds for the minimum evolution time between two states of a given system. Bounds of this evolution time, known as quantum speed limit time (QSLT), are intimately related to the evolution speed of quantum systems. The applications of these bounds are shown in different scenarios, including quantum communication, [1, 2] quantum metrology, [3, 4] quantum computation, [5] as well as quantum optimal control protocols.[6– 9] Derivations of these basic bounds focused on the closed system with unitary evolution, are obtained by the Mandelstam– Tamm (MT) type bound and Margolus– Levitin (ML) type bound.[10– 21] Moreover, the extensions of the QSLT for nonunitary evolution of open systems are also studied, [22– 27] since the relevant influence of the environment on processing or information transferring systems cannot be ignored. It is shown that two unified bounds of the minimum evolution time for the pure or mixed initial states including both MT and ML types for the nonunitary dynamics process have been formulated, respectively.[24, 25] These two unified bounds have already been used to illustrate the quantum evolution speed for a qubit state (whether it is a pure state or mixed state) under the decoherence process. We know that the correlated composite quantum states play a central role in quantum information and communication theory, [28– 32] such as, in order to fulfil a long-distance high-fidelity quantum communication in a noisy channel, the entanglement of a composite system (two distant sites) must be used to implement quantum repeaters.[33, 34] The QSLT on the evolution of an open composite quantum system would be helpful to analyze the robustness of quantum simulators and computers against decoherence.[35, 36] The application of these unified bounds to assess the evolution speed of the arbitrary states in the composite quantum system with nonunitary dynamics, is not well studied.
In this work, we are interested in the evolution speed of two-qubit Bell-diagonal states under certain noise channels (i.e., phase flip, bit flip, and bit– phase flip). By using of the unified bound of QSLT for arbitrary mixed states, [25] we have calculated the exact expressions of QSLT for the initial two-qubit Bell-diagonal states, which mainly depend on the parameters of the initial states and the decoherence channels. In the following, we also focus on the QSLT for the time-dependent states started from the initial Bell-diagonal states in the whole dynamics process. We demonstrate that the QSLT will be reduced gradually with the starting point in time under the noise channels, that is to say, the two-qubit system executes a speeded-up dynamics evolution process. Moreover, for certain initial Bell-diagonal states, a remarkable result we find is the existence of a sudden change of the decay rate of the QSLT at a certain critical time τ c. On the other hand, as we know that, at the same critical time τ c, a sudden transition from classical decoherence to quantum decoherence for this class of initial Bell-diagonal states also appears.[37] Then we can specifically point out that the evolution speed of the whole dynamics process can be described qualitatively by the classical decoherence for τ < τ c, and quantum decoherence for τ > τ c. Finally, we also recognize a symmetry among the above three decoherence channels.
Firstly, we start with the definition of the QSLT for open quantum systems. A unified lower bound, including both MT and ML types, has been derived in Ref. [25]. With the help of the von Neumann trace inequality and the Cauchy– Schwarz inequality, the QSLT between an arbitrary initially mixed state ρ 0 and its target state ρ τ D, governed by the master equation 

with 

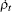
By considering two qubits without mutual interaction, we mainly focus on the phase flip, bit flip, and bit-phase flip channels as the decoherence processes. The dynamics of each qubit is governed by a master equation that gives rise to a completely positive trace-preserving map ε (· ). In the Born– Markov approximation, the operator-sum representation is given by
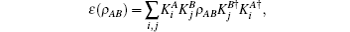
with 

where ci ∈ ℜ such that 0 ≤ | ci| ≤ 1 for i = 1, 2, 3, and IA(B) is the identity operator in subspace A(B). The state in Eq. (2) includes the Werner states (| c1| = | c2| = | c3| = c) and the Bell states (| c1| = | c2| = | c3| = 1).
We first focus on the phase flip channel. For this channel, the Kraus operators are given by[28, 37, 38]

here, pA(B) is used as the parametric time in channel A(B), and by considering the symmetric situation in which the decoherence rate is equal in both channels, so pA = pB = p. For the initial state of Eq. (2), the time evolution of the total system is

where

and 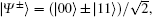

Now, we calculate the QSLT between the initial Bell-diagonal state ρ 0 to ρ τ D by the driving time τ D under the phase flip channel. According to the expression (1), we can clearly find that the distance between ρ 0 and ρ τ D, 
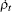
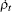

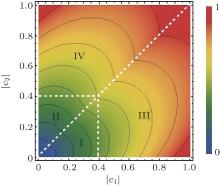
While for the initial state ρ 0, the singular values ρ i depend on the region of the coefficients ci. Then, in the following, we divide the region of the coefficients ci into four parts.
Case I If | c3| ≥ | c1| ≥ | c2| in Eq. (2), the singular values ρ i of the initial states ρ 0 satisfy 
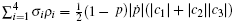
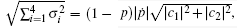

Case II If | c3| ≥ | c2| ≥ | c1| , the singular values ρ i of the initial states ρ 0 are equal to those in case I. So we obtain 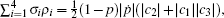
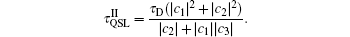
Case III When | c1| ≥ | c3| , | c2| , the singular values ρ i are given by 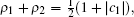
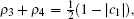



The QSLT does not depend on the coefficient c3.
Case IV Finally, if | c2| ≥ | c3| , | c1| , we acquire 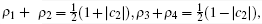
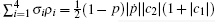

(also independent of the coefficient c3).
Inspection of the expressions 
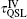
For the bit-flip channel, the Kraus operators are[15, 17]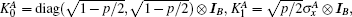
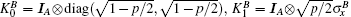

For | c3| ≥ | c1| , | c2| and | c2| ≥ | c1| , | c3| , under the bit-flip channel, the QSLT of the initial state does not depend on c1. The QSLT is symmetrical with respect to the line | c2| = | c3| , i.e., 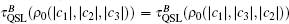
However, for the bit– phase-flip channel, the Kraus operators can be shown[28, 38]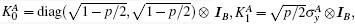
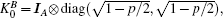

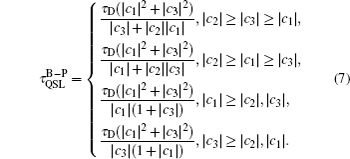
The fact that, for | c1| ≥ | c2| , | c3| and | c3| ≥ | c2| , | c1| , the coefficient c2 would not affect the QSLT under the bit– phase-flip channel. It is also simple to see that, for the bit– phase-flip channel,
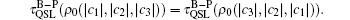
And the QSLTs for the initial states in cases | c2| ≥ | c3| ≥ | c1| and | c2| ≥ | c1| ≥ | c3| are always smaller than those for the states in cases | c1| ≥ | c2| , | c3| and | c3| ≥ | c2| , | c1| .
It is worth mentioning that the QSLT of any Bell-diagonal states under phase flip, bit flip, and bit– phase-flip channels, can be accurately calculated; this is one of our main results in this work. Particularly, for the initial Werner state (| c1| = | c2| = | c3| = c), the QSLTs under these three noise channels are all equal to 2τ D/(1+ 1/c), which is proportional to c.
In what follows, we shall illustrate the application of the QSLT to the quantum evolution speed of the whole dynamics process under different decoherence channels. The QSLT can demonstrate the speed of the dynamics evolution from a time-evolution state ρ τ to another ρ τ + τ D by a driving time τ D. It is easy to find that the time-evolution state ρ τ at any point in time also maintains the form of a Bell-diagonal state. So the QSLT starting from an arbitrary time-evolution state ρ τ to ρ τ + τ D can be calculated by the expressions of τ QSL in Section 2. We would examine the evolution speed of the whole dynamics process where the system starts from the two-qubit Bell-diagonal state in Eq. (2), under phase-flip, bit-flip, and bit– phase-flip channels, respectively.
First of all, under the phase flip channel, | c3| ≥ | c1| , | c2| is chosen for ρ 0. During the dynamics evolution process, c3 remains unchanged, so the condition | c3| ≥ | c1(τ )| , | c2(τ )| is fulfilled in τ ∈ [0, ∞ ). By considering an arbitrary mixed state ρ τ evolves to anotherρ τ + τ D under a driving time τ D, the QSLT can be calculated

From Eq. (8), one sees immediately that, the QSLT for the time-dependent state ρ τ decays monotonically with the evolution time γ τ , that is to say, in this case, the whole evolution of the two-qubit Bell-diagonal state can exhibit a speeded-up process under the local phase-flip noise channels. For the special case c3 = 1, c1 = c2 = 0, which means the system would not evolve any further under the phase-flip channels (i.e., ρ τ = ρ τ + τ D). Therefore, the minimum evolution time of ρ τ to ρ τ + τ D is 
However, if ρ 0 satisfies | c1| ≥ | c2| , | c3| or | c2| ≥ | c1| , | c3| , due to c3 independence of the evolution time, it is easy to find that, for τ ≤ τ c, with

the conditions | c1(τ )| ≥ | c2(τ )| , | c3| or | c2(τ )| ≥ | c1(τ )| , | c3| are always true. By considering the dynamics process τ ∈ [0, τ c], we can calculate the QSLT for the qubits to evolve from ρ τ to ρ τ + τ D,
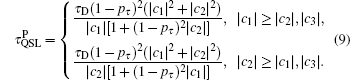
On the other hand, for τ > τ c, then | c3| ≥ | c1(τ )| ≥ | c2(τ )| or | c3| ≥ | c2(τ )| ≥ | c1(τ )| , so when τ ∈ (τ c, ∞ ), the expressions of QSLT can be obtained by Eq. (8). Hence, in the conditions | c1| ≥ | c2| , | c3| or | c2| ≥ | c1| , | c3| , we note that, the decay rate of the QSLT changes suddenly at τ = τ c. So we can conclude that, in the above case, the open system executes a speeded-up dynamics evolution process, but the increasing rate of the evolution speed would have a sudden change at τ = τ c. Let us, finally, study the QSLT, classical correlation and quantum correlation (quantum discord) on the class of initial states for which c1 = ± 1 and c2 = ∓ c3, with | c3| < 1, in Fig. 2. It is worth noting that, as noted in Ref. [37], for this initial condition, the behavior of sudden transition from classical correlation decoherence to quantum correlation decoherence can occur at τ = τ c, and at this time point, the decay rate of the QSLT can also change suddenly. Remarkably, the attenuations of the QSLT and classical correlation are synchronous in time until τ = τ c. However, for τ > τ c, the synchronous attenuation behavior occurs between the QSLT and quantum discord. This means that the speed of the dynamics evolution from a time-evolution state ρ τ to another ρ τ + τ D can be clearly signatured by the classical correlation of the time-evolution state ρ τ in the case τ < τ c. While for τ > τ c, we can use the quantum discord of ρ τ to describe the speed of the dynamics process, qualitatively. This is a newly noticed phenomenon.
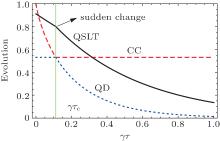 | Fig. 2. The QSLT (solid black line), classical correlation (CC, dashed red line), and quantum correlation (QD, dotted blue line) under local phase-flip channels as a function of the initial time parameter γ τ . We choose the class of initial Bell-diagonal states considered in Ref. [37], in which c1 = ± 1, c2 = ∓ c3, here c1 = 1, c2 = − 0.8, and c3 = 0.8, and the driving time τ D = 1. On this initial condition, the behavior of sudden transition from classical correlation decoherence to quantum correlation decoherence occurs at τ = τ c. The sudden change of the decay of QSLT has been marked in this figure. The classical correlation and quantum discord can be obtained by the method in Ref. [39]. |
Finally, when we consider the bit-flip and the bit– phase-flip channels, the behaviors of the evolution speed of the whole dynamics process under the phase-flip channel described above can also occur under other conditions on the ci in state (2). It is simple to see that, for the bit-flip and bit– phase-flip channels, the QSLT starting from an arbitrary time-evolution state ρ τ to ρ τ + τ D can be obtained with c1 and c2 replacing c3, respectively.
Based on the definition of the QSLT for arbitrary mixed states, we have calculated the expressions of the QSLT to characterize the speed of evolution for an open composite quantum system. In particular, for the initial two-qubit Bell-diagonal state, we have identified four different expressions of the QSLT under decoherence, which depend on the coefficients of the initial composite state and on the noise channel. So these different expressions of the QSLT can be used to characterize the maximal evolution speed of the initial two-qubit Bell-diagonal states under different nondissipative decoherence channels. Moreover, by studying the bound for the arbitrary time-dependent states started from a class of two-qubit states cited in Ref. [37], a remarkable feature has been demonstrated that the decay rate of the QSLT can change suddenly at a critical time τ c; at this moment, the behavior of sudden transition from classical decoherence to quantum decoherence also occurs. This evolution speed of the dynamics process would play an essential role in the understanding of the classical-to-quantum decoherence transition. Our results may be of interest in exploring the speed of quantum computation and quantum information processing under decoherence channels.
Firstly, we calculate the QSLT for the initial Bell-diagonal state ρ 0 in Eq. (2) under the bit-flip channel. For this channel, c1 remains unchanged. Then the space of the initial state ρ 0 and the target state ρ τ D can be obtained 
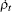
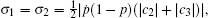
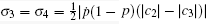
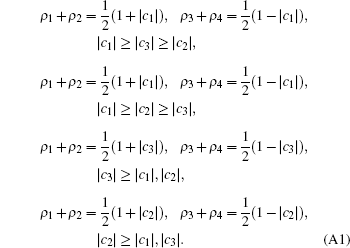
Similar to the phase-flip channel, we can obtain that 

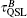
With regard to the QSLT in the bit– phase-flip channels, where c2 remains unchanged during the evolution process, we can also find 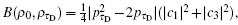
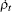



Then we obtained 
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|