Cite this Article
Wang Bao-Ying, Gong Yu-Bing. Effects of channel noise on synchronization transitions in delayed scale-free network of stochastic Hodgkin–Huxley neurons* . Chinese Physics B, 24(11): 118702  
Permissions
Effects of channel noise on synchronization transitions in delayed scale-free network of stochastic Hodgkin–Huxley neurons*
Wang Bao-Yinga), Gong Yu-Bingb)
Library, Ludong University, Yantai 264025, China
School of Physics and Optoelectronic Engineering, Ludong University, Yantai 264025, China

†Corresponding author. E-mail: gongyubing@ustc.edu

*Project supported by the Natural Science Foundation of Shandong Province of China (Grant No. ZR2012AM013).

Abstract

We numerically study the effect of the channel noise on the spiking synchronization of a scale-free Hodgkin–Huxley neuron network with time delays. It is found that the time delay can induce synchronization transitions at an intermediate and proper channel noise intensity, and the synchronization transitions become strongest when the channel noise intensity is optimal. The neurons can also exhibit synchronization transitions as the channel noise intensity is varied, and this phenomenon is enhanced at around the time delays that can induce the synchronization transitions. It is also found that the synchronization transitions induced by the channel noise are dependent on the coupling strength and the network average degree, and there is an optimal coupling strength or network average degree with which the synchronization transitions become strongest. These results show that by inducing synchronization transitions, the channel noise has a big regulation effect on the synchronization of the neuronal network. These findings could find potential implications for the information transmission in neural systems.

Keyword: 87.19.lc; 87.19.lm; 87.19.lj; channel noise; scale-free network; time delay; synchronization transition
1. Introduction

The cerebral cortex is a highly interconnected network of neurons, and structural and functional brain networks in humans and other animals have witnessed small-world architectures over a wide range of scales in both space and time.[1– 4] Meanwhile, by using functional magnetic resonance imaging, power-law distributions were obtained upon linking correlated fMRI voxels, [5] and the robustness against simulated lesions of anatomic cortical networks has also been found to rely mostly on the scale-free structure.[6] Synchronization is an important phenomenon that occurs in many biological and physical systems, and it has been extensively studied in many realistic systems, such as neuronal networks, biological systems, ecological systems, and so on.[7, 8] In biological systems, the synchronization phenomenon is of significance to the information transmission in the neural systems, and particularly, it is correlated with many physiological mechanisms of normal and pathological brain functions.[9– 13] In recent decades, many synchronization phenomena have been found in various neuronal systems, such as coupling-induced synchronization in coupled bursting neurons[14– 16] and small-world neuronal networks, [17, 18] adaptive coupling-enhanced synchronization in delayed neuronal networks, [19] synchronization induced by subthreshold stimulus and time delay in neuronal networks, [20– 27] and frequency synchronization induced by the arrangement of heterogeneous neurons in a ring-coupled neuronal network.[28] In recent years, a novel phenomenon of synchronization transitions has gained growing attention, and many phenomena of synchronization transitions induced by time delay and neuronal coupling have been found in coupled neurons and neuronal networks.[29– 40]

Neurons are noisy units. Neuronal noise arises from many different sources, such as the quasi-random release of neurotransmitters by synapses and the random synaptic input from other neurons (external synaptic noise), as well as the random switching of ion channels (internal channel noise). The synaptic noise reflects the stochastic dynamics of chemical reactions occurring in synapses and can also represent the influence of the external fluctuation, while the channel noise reflects the fluctuation arising from stochastic opening– closing of the channel gates, which is inherent to the neurons. Therefore, the channel noise could be more important than the synaptic noise in neuronal systems. Since the pioneering work on neuronal dynamics by Hodgkin and Huxley, [41] the role of noise in the generation and propagation of the membrane potential of neurons has been extensively studied, and stochastic resonance (SR) and coherence resonance (CR) have been found in various neuronal systems.[42– 44] In recent years, many noisy phenomena have been found in various neuronal systems, for example, SR in hybrid scale-free neuronal networks, [45] spatial CR in excitable media[46] and neuronal networks, [47] channel noise CR in neuronal networks, [48, 49] correlated Gaussian noise optimized mean firing rate in two-dimension neuronal networks, [50] noise enhanced propagation of pacemaker signals and weak signal across neuronal networks, [51– 53] and channel noise decreased mean latency and jitter of the first spikes in response to sub-threshold signal[54, 55] and degraded signal detection capability of neuronal networks, [56] phase noise-enhanced response to subthreshold signals in a Hodgkin– Huxley (HH) neuron, [57] channel blocking on the spatiotemporal dynamics of neuronal networks, [58] the effect of inhomogeneous distribution of ion channels on collective electric activities of neurons in a ring network, [59] and double CR in FitzHugh– Nagumo neuron driven by harmonic velocity noise.[60] In addition, the noise-enhanced synchronization has been found in excitable media, [61] thermally sensitive neurons, [62] and scale-free neuronal networks.[63] Very recently, synchronization transitions induced by the synaptic noise have also been observed in neuronal networks.[64] However, it is not clear if and how the channel noise can induce synchronization transitions in neuronal networks.

In this paper, we study the effect of the channel noise on the synchronization of scale-free HH neuron networks with time delays. We aim to investigate how the channel noise influences the synchronization of the neuronal network, and particularly, whether the channel noise can induce synchronization transitions in the neuronal network. We first study the effect of the channel noise on the synchronization transitions induced by time delay, and then investigate how the channel noise induces the synchronization transitions in the neuronal networks. The effects of coupling strength and network average degree are studied and the mechanisms are briefly discussed. Finally, we conclude this study.

2. Model and equations

The dynamics of the membrane potentials of a stochastic HH neuron is given by

where capacity C = 1  μ F· cm− 2; VNa = 50  mV, VK = − 77  mV, VL = − 54.4  mV are the reversal potentials for the sodium, potassium, and leakage currents, respectively; gK = 36  mS· cm− 2 and gNa = 120  mS· cm− 2 are the maximal conductances of the potassium and sodium ions, respectively, and GL = 0.3mS · cm− 2 is the leakage conductance. The opening and closing rates of gating variables m, h, and n are

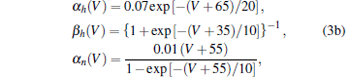And ξ m, n, h (t) are Gaussian white noises with zero mean and auto-correlation functions

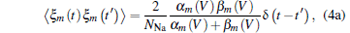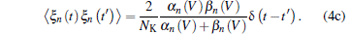With an assumption of homogeneous ion channel densities ρ Na = 60  μ m− 2 and ρ K = 18  μ m− 2, the numbers of sodium and potassium ion channels on membrane patch size S are given by NNa = ρ NaS and NK = ρ KS, respectively. The intensity of channel noise is determined by patch size S, and the smaller S corresponds to bigger noise intensity.

We employ the scale-free network developed by Barabá si and Albert.[65] The present network comprising N = 100 neurons starts with m0 connected nodes, and subsequently every new node is attached to m (≤ m0) different nodes already present in the network, whereby the probability p that a new node will be connected to node i depends on its degree ki in accordance with . This growth and preferential attachment scheme yields a network with an average degree and a power-law degree distribution with the slope of the line equaling − 2.9 on a double logarithmic graph. Here, we set m = m0.

The membrane potential dynamics of the delayed scale-free stochastic HH neuron network can be written as

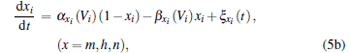where Vi is the membrane potential of neuron i (1 ≤ i ≤ N); ∑ jɛ i j [Vj (t − τ ) − Vi (t)] is the delayed electrical coupling; and ɛ ij is the coupling strength, ɛ ij = ɛ if there is coupling between neurons i and j, and ɛ ij = 0 otherwise; Vj (t − τ ) is the membrane potential of neuron j at earlier time t − τ , where τ (in units of ms) is the information transmission delay between neurons i and j, and the summation takes over all neurons.

The synchronization of the neuronal network is quantified by standard deviation σ defined as[66]

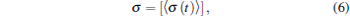with

where 〈 · 〉 denotes the average of σ (t) over time, and [· ] is the average over different network realizations for each set of parameters. Larger σ (t) represents larger deviation between the neurons, and smaller σ (t) shows higher synchronization.

Numerical integrations of Eqs.  (5a) and (5b) are carried out using the explicit Euler algorithm with a time step of 0.001  ms. The parameters of all neurons are assumed to be identical except for distinct initial values of the potential Vi0.

3. Results and discussion
3.1. Effect of channel noise on synchronization transitions induced by time delay

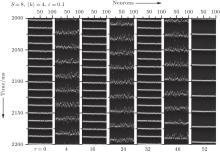
In this section, we study how the channel noise influences the synchronization transitions induced by time delays. Let 〈 k〉 = 4 and ɛ = 0.1. In Fig.  1, we display the spatiotemporal patterns of the membrane potentials of the neurons for different time delays τ when patch size S = 8 μ m2. It is seen that the neurons intermittently become synchronous and non-synchronous as τ increases, exhibiting synchronization transitions. Quantitative characterization of this phenomenon by standard deviation σ plotted against τ is displayed in Fig.  2. It is seen that σ passes through a few peaks as τ increases (see the green curve).

Fig.  1. Spatiotemporal patterns of the membrane potentials for different time delays τ at 〈 k〉 = 4, ɛ = 0.1, and S = 8. The neurons intermittently become synchronous and non- synchronous as τ increases, exhibiting synchronization transitions.

Fig.  2. The σ in dependence on τ for different S at 〈 k〉 = 4 and ɛ = 0.1. For intermediate S, the σ peaks grow and become higher, indicating that the synchronization transitions induced by time delay are stronger.

Now we study the effect of the channel noise on the synchronization transitions induced by time delay. In Fig.  2, σ is also plotted as a function of τ for different patch sizes S. For small patch size S = 1  μ m2, the σ peaks are very low, indicating that there are very weak synchronization transitions. As S increases, the σ peaks grow and become highest at around intermediate patch sizes S = 8– 15  μ m2, and then they become low again. This shows that the synchronization transitions by time delay closely depend on the channel noise and occur only when the channel noise intensity is proper, and particularly, the synchronization transitions become strongest when the channel noise is optimal. It is also shown in Fig.  2 that the σ peaks make a shift to larger τ as S increases, which represents that the time delay for inducing the synchronization transitions increases as the channel noise intensity decreases.

This phenomenon can be understood as follows. The information transmission delay introduces phase slips in the firing activity of neurons and adjusts the phases of the neurons, and this can make the neurons become synchronous or non-synchronous, exhibiting the synchronization transitions. On the other hand, without external stimuli and synaptic noise, the channel noise is required to make the neurons fire a spike train. When the channel noise intensity is too high (i.e., too small S), the spiking behaviors of the neurons are disordered and non-synchronous; when the channel noise intensity is too low (i.e., too big S), the neurons fire few spikes, and it is also difficult for the spiking behaviors to become synchronous; for an intermediate channel noise intensity, the spiking behaviors are moderately synchronized, and the time delay can change the phases of the spiking behaviors easily. Therefore, the synchronization transitions by time delay are stronger and strongest when the channel noise intensity is intermediate and optimal.

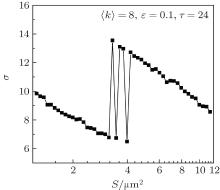
3.2. Synchronization transitions induced by channel noise

In this section, we study if and how the channel noise induces synchronization transitions in the neuronal network. We set 〈 k〉 = 8, ɛ = 0.1, and τ = 24. In Fig.  3, the spatiotemporal patterns of the membrane potentials of the neurons for different patch sizes S are displayed. It is seen that the neurons intermittently become synchronous and non-synchronous as S increases, performing synchronization transitions. This phenomenon is quantified via σ in dependence on S in Fig.  4. It is seen that σ passes through a few peaks as S increases from 3.2 to 4.2, which shows that the channel noise can induce synchronization transitions.

Fig.  3. Spatiotemporal patterns of the membrane potentials for different S at 〈 k〉 = 8, ɛ = 0.1, and τ = 24. As S increases, the neurons intermittently become synchronous and non-synchronous, exhibit synchronization transitions.

Fig.  4. Dependence of σ on D at 〈 k〉 = 8, ɛ = 0.1, and τ = 24. As S increases, σ passes through a few peaks within a narrow range of patch size (2.6  μ m2 < S < 4.2  μ m2), which quantitatively characterizes the occurrence of the synchronization transitions.

We have also studied the synchronization transitions by channel noise for other time delays, and the results are presented via a contour plot of σ as functions of S and τ in Fig.  5. It is seen that σ changes in zigzag shape at time delays around τ = 24 and τ = 43, which indicates the occurrence of synchronization transitions. This shows that the synchronization transitions are delay-dependent and enhanced at around the time delays that can induce synchronization transitions. The spiking behaviors at around the time delays that can induce synchronization transitions are more sensitive to the disturbance of noise, and their phases can be changed by noise more easily, and thus the synchronization transitions by the channel noise are stronger at around these time delays.

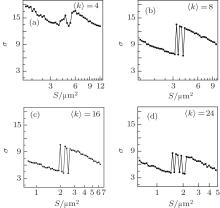
Fig.  5. Contour plot of σ as functions of S and τ at 〈 k〉 = 8 and ɛ = 0.1. For certain time delays, σ changes in zigzag shape as S increases, indicating the occurrence of the synchronization transitions induced by the channel noise.

In what follows, we study the effects of coupling strength ɛ and network average degree 〈 k〉 . In Fig.  6, σ is plotted against S for different ɛ at 〈 k〉 = 8 and τ = 24. For small coupling strength ɛ = 0.05, σ changes a little as S increases, which indicates that the synchronization transitions are very weak. As ɛ increases, the σ peaks grow higher and become highest at ɛ = 0.1, and then they drop again and become very low at ɛ = 0.9. This shows that there is an optimal coupling strength with which the synchronization transitions by the channel noise become strongest. This phenomenon can be discussed briefly. For too small coupling strength, the neurons are coupled so weakly that the spiking behaviors have a low synchronization, and it is difficult for the channel noise to make the neurons exhibit synchronization transitions, and thus the synchronization transitions are very weak; for too large coupling strength, the neurons are highly synchronized, and it is also difficult for the channel noise to make the neurons exhibit synchronization transitions; for an intermediate coupling strength, the spiking behaviors are moderately synchronized and can be changed by the channel noise more easily. Therefore, the synchronization transitions are stronger and strongest when the coupling strength is proper and optimal.

Fig.  6. The σ in dependence on D for different coupling strengths ɛ at 〈 k〉 = 8 and τ = 24. As ɛ increases, the σ peaks grow and become highest at around intermediate ɛ = 0.1, and then become low again. This indicates that there is an optimal coupling strength with which the synchronization transitions by channel noise become strongest.

In Fig.  7, σ is plotted against S for different average degrees of 〈 k〉 at ɛ = 0.1 and τ = 24. As 〈 k〉 increases, the σ peaks grow and become highest at around 〈 k〉 = 8, and then become low again. This shows that there is an optimal average degree by which the synchronization transitions by the channel noise become strongest. The network average degree reflects the intensity of connections among the neurons. When the average degree is optimal, the firing behaviors can be changed by the channel noise more easily. Therefore, the synchronization transitions by the channel noise are stronger and strongest when the average degree is proper and optimal.

Fig.  7. Dependence of σ on D for different average degrees 〈 k〉 at ɛ = 0.1 and τ = 24. As 〈 k〉 increases, the σ peaks grow and become highest at around 〈 k〉 = 8, and then become low again. This indicates that there is an optimal average degree with which the synchronization transitions by channel noise become strongest.

From Figs.  6 and 7, it is also found that the σ peaks move to a smaller S as ɛ or 〈 k〉 increases. This shows that the channel noise for the synchronization transitions increases as the coupling strength or average degree increases, this is because the synchronization of the neurons increases as the coupling strength or average degree increases.

The synchronization transitions induced by the channel noise can be briefly explained as follows. The time delay can introduce phase slips in the neuronal firing behaviors and can induce synchronization transitions in the neuronal network.[30, 67] In the absence of external stimuli and external noise, the channel noise is required for the neurons to fire spike trains. Under different channel noise intensities, the neurons can fire spikes with different phases, and in this case, a phase slip introduced by the time delay has different effects on these spiking behaviors. Therefore, the spiking behaviors intermittently become synchronous or non-synchronous when the channel noise is varied, exhibiting the synchronization transitions.

As stated in the introduction, synchronization is correlated with many physiological mechanisms of normal and pathological brain functions. Physiological experiments have demonstrated the existence of synchronous firing in different areas of the brain of some animals like cats and monkeys. The synchronization of coupled neurons has been suggested as a mechanism for binding globally distributed into a coherent motion, and the presence or absence of synchronization can result in normal function or dysfunction of a biological system, and too much synchrony can lead to disease.[9– 12] The synchronization transitions by channel noise show that the channel noise can intermittently enhance and reduce the synchronization of the neuronal network, and thus could have a subtle regulation effect on the normal and pathological functions in the brain. These findings may find potential implications for the information transmission in neural systems like the brain.

It should be noted that the present work is different from the previous works by Sun et al.[68] and Ao et al.[69] In Ref.  [68], Sun et al. studied the effect of the channel block on the spiking regularity in clustered neuronal networks and found that the spiking regularity can be resonantly enhanced by fine-tuning of the non-blocked channels. In Ref.  [69], Ao et al. investigated the effects of the channel noise on the spiking dynamics of two coupled stochastic HH neurons, and they found that the time delay can induce in-phase and anti-phase transitions, and the phenomenon changes with varying channel noise level. In this work, we study the effect of the channel noise on the synchronization of a scale-free stochastic HH neuron network with time delays and observe the channel noise-induced synchronization transitions. Therefore, the model of neuronal network studied and the phenomena observed in this paper are different from those in the previous studies.

4. Conclusion

We have numerically studied the effect of the channel noise on the synchronization of a scale-free HH neuron network with time delays. It is found that the time delay can induce synchronization transitions when the channel noise intensity is intermediate and proper, and the phenomenon becomes strongest when the channel noise intensity is optimal. More importantly, the channel noise can also induce synchronization transitions in the neuronal network, and the phenomenon is delay-dependent and enhanced at around the time delays that can induce synchronization transitions. This phenomenon also depends on the coupling strength and the network average degree, and becomes strongest when the coupling strength or network average degree is optimal. These results show that the channel noise has a subtle regulation effect on the synchronization of the neuronal network. This implies that the channel noise could play an important role in the information transmission in neural systems like the brain.

Reference
1 Salvador R, Suckling J, Coleman M R, Pickard J D, Menon D and Bullmore E 2005 Cereb. Cortex 15 1332 [Cited within:1]
2 Reijneveld J C, Ponten S C, Berendse H W and Stam C J 2007 Neurophysiology 118 2317 DOI:10.1016/j.clinph.2007.08.010 [Cited within:1]
3 Stam C J and Reijneveld J C 2007 Nonlin. Biomed. Phys. 1 3 DOI:10.1186/1753-4631-1-3 [Cited within:1]
4 Honey C J, Kotter R, Breakspear M and Sporns O 2007 Proc. Nat. Acad. Sci. USA 104 10240 DOI:10.1073/pnas.0701519104 [Cited within:1]
5 Eguíluz V M, Chialvo D R, Cecchi G A, Baliki M and Apkarian A V 2005 Phys. Rev. Lett. 94 018102 DOI:10.1103/PhysRevLett.94.018102 [Cited within:1]
6 Kaiser M, Martin R, Andras P and Young M P 2007 Eur. J. Neurosci. 25 3185 DOI:10.1111/j.1460-9568.2007.05574.x [Cited within:1]
7 Arenas A, Díaz-Guilera A, Kurths J, Moreno Y and Zhou C S 2008 Phys. Rep. 469 93 DOI:10.1016/j.physrep.2008.09.002 [Cited within:1]
8 Suykens J A K and Osipov G V 2008 Chaos 18 037101 DOI:10.1063/1.2985139 [Cited within:1]
9 Gray C M and Singer W 1989 Proc. Natl. Acad. Sci. USA 86 1698 DOI:10.1073/pnas.86.5.1698 [Cited within:2]
10 Bazhenov M, Stopfer M, Rabinovich M, Huerta R, Abarbanel H D I, Sejnowski Y J and Laurent G 2001 Neuron 30 553 DOI:10.1016/S0896-6273(01)00284-7 [Cited within:1]
11 Mehta M R, Lee A K and Wilson M A 2001 Nature 417 741 [Cited within:1]
12 Levy R, Hutchison W D, Lozano A M and Dostrovsky J O 2000 J. Neurosci. 20 7766 [Cited within:1]
13 Mormann F, Kreuz T, Andrzejak R G, David P, Lehnertz K and Elger C E 2003 Epilepsy. Res. 53 173 DOI:10.1016/S0920-1211(03)00002-0 [Cited within:1]
14 Bahar S 2004 Fluct. Noise Lett. 4 L87 DOI:10.1142/S0219477504001690 [Cited within:1]
15 Wang Q Y, Lu Q S and Chen G R 2007 Physica A 374 869 DOI:10.1016/j.physa.2006.08.062 [Cited within:1]
16 Yoshioka M 2005 Phys. Rev. E 71065203R DOI:10.1103/PhysRevE.71.0652032005 [Cited within:1]
17 Zheng Y H and Lu Q S 2008 Physica A 387 3719 DOI:10.1016/j.physa.2008.02.039 [Cited within:1]
18 Hasegawa H 2005 Phys. Rev. E 72 056139 DOI:10.1103/PhysRevE.72.056139 [Cited within:1]
19 Wang L, Gong Y B, Xu B and Wu Y N 2013 Sci. China Chem. 56 648 DOI:10.1007/s11426-013-4836-6 [Cited within:1]
20 Wang Q Y, Lu Q S and Chen G R 2007 Europhys. Lett. 77 10004 DOI:10.1209/0295-5075/77/10004 [Cited within:1]
21 Wang Q Y, Murks A, Perc M and Lu Q S 2011 Chin. Phys. B 20 040504 DOI:10.1088/1674-1056/20/4/040504 [Cited within:1]
22 Dhamala M, Jirsa V K and Ding M Z 2004 Phys. Rev. Lett. 92 074104 DOI:10.1103/PhysRevLett.92.074104 [Cited within:1]
23 Rossoni E, Chen Y H, Ding M Z and Feng J F 2005 Phys. Rev. E 71 061904 DOI:10.1103/PhysRevE.71.061904 [Cited within:1]
24 Roxin A, Brunel N and Hansel D 2005 Phys. Rev. Lett. 94 238103 DOI:10.1103/PhysRevLett.94.238103 [Cited within:1]
25 Ko T W and Ermentrout G B 2007 Phys. Rev. E 76 056206 DOI:10.1103/PhysRevE.76.056206 [Cited within:1]
26 Burić N, Todorović K and Vasović N 2008 Phys. Rev. E 78 036211 DOI:10.1103/PhysRevE.78.036211 [Cited within:1]
27 Adhikari B, Prasad A and Dhamala M 2011 Chaos 21 023116 DOI:10.1063/1.3584822 [Cited within:1]
28 Sun X J, Yang B H, Wu Y and Xiao J H 2014 Acta Phys. Sin. 63 180507(in Chinese) [Cited within:1]
29 Wang Q Y, Lu Q S and Chen G R 2008 Int. J. Bifurcat. Chaos 18 1189 DOI:10.1142/S0218127408020914 [Cited within:1]
30 Wang Q Y, Duan Z S, Perc M and Chen G R 2008 Europhys. Lett. 83 50008 DOI:10.1209/0295-5075/83/50008 [Cited within:1]
31 Wang Q Y, Perc M, Duan Z S and Chen G R 2009 Phys. Rev. E 80 026206 DOI:10.1103/PhysRevE.80.026206 [Cited within:1]
32 Wang Q Y, Perc M, Duan Z S and Chen G R 2010 Physica A 389 3299 DOI:10.1016/j.physa.2010.03.031 [Cited within:1]
33 Wang Q Y, Chen G R and Perc M 2011 PLoS One 6 e15851 DOI:10.1371/journal.pone.0015851 [Cited within:1]
34 Guo D Q, Wang Q Y and Perc M 2012 Phys. Rev. E 85 061905 DOI:10.1103/PhysRevE.85.061905 [Cited within:1]
35 Hao Y H, Gong Y B, Wang L, Ma X G and Yang C L 2011 Chaos Soliton. Fract. 44 260 DOI:10.1016/j.chaos.2011.02.005 [Cited within:1]
36 Xu B, Gong Y B, Wang L and Wu Y N 2013 Nonlin. Dyn. 72 79 DOI:10.1007/s11071-012-0691-9 [Cited within:1]
37 Gong Y B, Lin X, Wang L and Hao Y H 2011 Sci. China Chem. 54 1498 DOI:10.1007/s11426-011-4363-2 [Cited within:1]
38 Sun X J, Lei J Z, Perc M, Kurths J and Chen G R 2011 Chaos 21 016110 DOI:10.1063/1.3559136 [Cited within:1]
39 Hu G and Huang X H 2014 Chin. Phys. B 23 108703 DOI:10.1088/1674-1056/23/10/108703 [Cited within:1]
40 Jia B 2014 Chin. Phys. B 23 050510 DOI:10.1088/1674-1056/23/5/050510 [Cited within:1]
41 Hodgkin A L and Huxley A F 1952 J. Physiol. 117 500 DOI:10.1113/jphysiol.1952.sp004764 [Cited within:1]
42 Gammaitoni L, Hänggi P, Jung P and Marchesoni F 1998 Rev. Mod. Phys. 70 223 DOI:10.1103/RevModPhys.70.223 [Cited within:1]
43 Schmid G, Goychuk I and Hänggi P 2001 Europhys. Lett. 56 22 DOI:10.1209/epl/i2001-00482-6 [Cited within:1]
44 Hänggi P 2002 ChemPhysChem 3 285 DOI:10.1002/1439-7641(20020315)3:3<285::AID-CPHC285>3.0.CO;2-A [Cited within:1]
45 Yilmaz E, Uzuntarla M, Ozer M and Perc M 2013 Physica A 392 5735 DOI:10.1016/j.physa.2013.07.011 [Cited within:1]
46 Perc M 2005 Phys. Rev. E 72 016207 DOI:10.1103/PhysRevE.72.016207 [Cited within:1]
47 Sun X J, Perc M, Lu Q S and Kurths J 2008 Chaos 18 023102 DOI:10.1063/1.2900402 [Cited within:1]
48 Ozer M, Perc M and Uzuntarla M 2009 Europhy. Lett. 86 40008 DOI:10.1209/0295-5075/86/40008 [Cited within:1]
49 Sun X J, Lei J Z, Perc M, Lu Q S and Lv S J 2011 Eur. Phys. J. B 79 61 DOI:10.1140/epjb/e2010-10031-3 [Cited within:1]
50 Sun X J, Perc M, Lu Q S and Kurths J 2010 Chaos 20 033116 DOI:10.1063/1.3483876 [Cited within:1]
51 Perc M 2007 Phys. Rev. E 76 066203 DOI:10.1103/PhysRevE.76.066203 [Cited within:1]
52 Ozer M, Perc M and Uzuntarla M 2009 Phys. Lett. A 373 964 DOI:10.1016/j.physleta.2009.01.034 [Cited within:1]
53 Ozer M, Perc M, Uzuntarla M and Koklukaya E 2010 Neuroreport 21 338 DOI:10.1097/WNR.0b013e328336ee62 [Cited within:1]
54 Ozer M, Uzuntarla M, Perc M and Graham L 2009 J. Theor. Biol. 261 83 DOI:10.1016/j.jtbi.2009.07.006 [Cited within:1]
55 Uzun R, Ozer M and Perc M 2014 Europhys. Lett. 105 60002 DOI:10.1209/0295-5075/105/60002 [Cited within:1]
56 Uzuntarla M, Uzun R, Yilmaz E, Ozer M and Perc M 2013 Chaos Soliton. Fract. 56 202 DOI:10.1016/j.chaos.2013.08.009 [Cited within:1]
57 Kang X S, Liang X M and Lü H P 2013 Chin. Phys. Lett. 30 018701 DOI:10.1088/0256-307X/30/1/018701 [Cited within:1]
58 Wu Y, Liu S B and Wang R 2013 Acta Phys. Sin. 62 220504(in Chinese) DOI:10.7498/aps.62.220504 [Cited within:1]
59 Wu X Y, Ma J X and Zhen B 2013 Acta Phys. Sin. 62 240507(in Chinese) DOI:10.7498/aps.62.240507 [Cited within:1]
60 Song Y L 2014 Chin. Phys. B 23 080504 DOI:10.1088/1674-1056/23/8/080504 [Cited within:1]
61 Neiman A, Schimansky-Geier A, Cornell-Bell A and Moss F 1999 Phys. Rev. Lett. 83 4896 DOI:10.1103/PhysRevLett.83.4896 [Cited within:1]
62 Zhou C S and Kurths J 2003 Chaos 13 401 DOI:10.1063/1.1493096 [Cited within:1]
63 Perc M 2009 Biophys. Chem. 141 175 DOI:10.1016/j.bpc.2009.01.012 [Cited within:1]
64 Wu Y N, Gong Y B and Wang Q 2014 Eur. Phys. J. B 87 198 DOI:10.1140/epjb/e2014-50437-1 [Cited within:1]
65 Barabási A L and Albert R 1999 Science 286 509 DOI:10.1126/science.286.5439.509 [Cited within:1]
66 Gong Y B, Xu B, Xu Q, Yang C L, Ren T Q, Hou Z H and Xin H W 2006 Phys. Rev. E 73 046137 DOI:10.1103/PhysRevE.73.046137 [Cited within:1]
67 Wang Q Y, Lu Q S, Chen G R, Feng and Duan L X 2009 Chaos Soliton. Fract. 39 918 DOI:10.1016/j.chaos.2007.01.061 [Cited within:1]
68 Sun X J and Shi X 2014 Sci. China Tech. Sci. 57 879 DOI:10.1007/s11431-014-5529-x [Cited within:2]
69 Ao X, Hänggi P and Schmid G 2013 Math. Biosci. 245 49 DOI:10.1016/j.mbs.2013.02.007 [Cited within:2]