Cite this Article
Zhang Yao-Yang, Hua Yun-Feng, Deng Zhen-Yu. Driven self-assembly of hard nanoplates on soft elastic shells* . Chinese Physics B, 24(11): 118202  
Permissions
Driven self-assembly of hard nanoplates on soft elastic shells*
Zhang Yao-Yanga), Hua Yun-Fengb), Deng Zhen-Yub)
Department of Civil Engineering, Tsinghua University, Beijing 100084, China
Department of Physics, Zhejiang University, Hangzhou 310027, China

†Corresponding author. E-mail: dengbug@gmail.com

*Project supported by the National Natural Science Foundation of China (Grant No. 21174131).

Abstract

The driven self-assembly behaviors of hard nanoplates on soft elastic shells are investigated by using molecular dynamics (MD) simulation method, and the driven self-assembly structures of adsorbed hard nanoplates depend on the shape of hard nanoplates and the bending energy of soft elastic shells. Three main structures for adsorbed hard nanoplates, including the ordered aggregation structures of hard nanoplates for elastic shells with a moderate bending energy, the collapsed structures for elastic shells with a low bending energy, and the disordered aggregation structures for hard shells, are observed. The self-assembly process of adsorbed hard nanoplates is driven by the surface tension of the elastic shell, and the shape of driven self-assembly structures is determined on the basis of the minimization of the second moment of mass distribution. Meanwhile, the deformations of elastic shells can be controlled by the number of adsorbed rods as well as the length of adsorbed rods. This investigation can help us understand the complexity of the driven self-assembly of hard nanoplates on elastic shells.

Keyword: 82.35.Np; 82.70.Dd; 82.20.Wt; self-assembly; nanoplate; elastic shell
1. Introduction

Self-assembly behavior has received great attention for potential applications in nanoscience and nanotechnology.[1– 8] Aggregation of proteins into functional nanomachines, [9] trimeric proteins into a desired symmetric structure, [10, 11] pH-induced self-assembly of peptide-amphiphile into nanofibers, [12] packing of phospholipids into biological membranes, [12] and aggregation of colloidal nanoparticles into crystalline[13] are just a few examples of self-assembly processes. Understanding the physical mechanisms driving self-assembly of biological or artificial components can reveal critical biological processes, and hold promise in the regulation and shaping of nanomaterial in the micrometer range or smaller size.

Elastic surfaces are ubiquitous in nature, and the mechanical properties of these surfaces play an important role both in their biological function and in their wide usage in material engineering.[5] The simplest and most important example of elastic surfaces is biological membrane. The main constituents of biological membranes are phospholipids-amphiphilic molecules, and biological membranes are constantly in contact with various macromolecules that either reside on their surface, or are being transported between the cell and its environment as well as shuffled between different compartments within eukaryotic cells. Since a lipid membrane is only permeable to small uncharged molecules and water, all macromolecules are required to interact with it or cross it. Therefore, self-assembly on biological membranes is an inevitable step in cellular transportation, signaling and recognition.[14] The elastic surface has revolutionized the field of self-assembly by providing a universal mechanism through which arbitrary building blocks can be driven close to each other. The stiffness of an elastic substrate can alter the morphology and dynamics of the tissue cells adhering to it, [15] and there are variable cytoskeleton assembly[16] and cell spreading on substrates of different mechanical properties.[17] Moreover, the surfaces’ response to external stress has been exploited in metrology[18, 19] and in the production of micro- and nano-scale patterned surfaces that may serve as components with novel optical, electronic and magnetic properties.[20]

The idea of using elastic surfaces as a means of driving self-assembly of arbitrary building blocks was first introduced by Whitesides et al.[21] Millimeter-size microchips and micro-components have been successfully self-assembled by manipulating the tension of the interface as well as by tailoring the chemistry of the building blocks.[22] When noninteracting hard particles bind to a deformable elastic shell, some very fantastic phenomena are observed.[3– 6, 23– 25] For example, nanoparticles adhering to the outer surface of an elastic nanotube can self-assemble into linear structures as a result of curvature-mediated interactions.[3] The nontrivial elastic response to deformations of soft elastic surfaces can lead to anisotropic interactions between the nanoparticles resulting in aggregation with different geometrical features, and the morphology of the patterns can be controlled by the mechanical properties of the surface and the strength of the nanoparticle adhesion.[5] Hard nanoparticles binding to a deformable elastic shell can self-assemble into a variety of linear patterns.[6]

Recently, focus has shifted to the development of novel fabrication techniques for various shapes, such as cubes, rods, plates and pyramidal particles.[26] In fact, the shape of nanoparticles plays an important role in the self-assembly behaviors. For example, nanocrystals often exhibit well-defined facets that result in a three-dimensional (3D) polyhedral shape or in a polygonal two-dimensional (2D) shape. The self-assembly of such faceted particles enables the formation of highly ordered superlattices, and it is dominated by driving forces that maximize face-to-face contact.[27– 29] More recently, a joint experimental-computational multiscale investigation of a class of highly faceted planar lanthanide fluoride nanoplates was performed, and the nanoplates can self-assemble into long-range ordered tilings at the liquid-air interface formed by a hexane wetting layer. The combination of shape-induced entropic and edge-specific energetic effects directs the formation of long-range ordered assemblies, [30] and a series of monodisperse faceted nanocrystals that include circular, rhombic and irregular hexagonal plates, as well as tetragonal bipyramids, are experimentally observed.[30– 32] In this paper, we use molecular dynamics (MD) simulation method to study the self-assembly behaviors of nanoplates on elastic shells. As the nanoplate has a two-dimensional structure and the soft elastic shell is also quasi-two-dimensional one, the self-assembly processes of nanoplates on soft elastic shells may be interesting. Understanding the critical physical mechanisms of driving self-assembly will illuminate the key physical processes and simultaneously it is possible to aggregate new materials with novel functional, biochemical and optical properties.

2. Model

As depicted in Fig.  1(a), the elastic surface is modeled by connecting beads into a triangular network.[33, 34] To prevent overlap between any two surface monomers, the monomers interact with each other via a purely repulsive truncated and shifted Lennard– Jones potential[6, 23, 24]

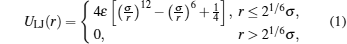where r denotes the distance between the centers of two surface monomers, σ is the monomer diameter, and ɛ = 1.0kBT.

Fig.  1. (a) Detailed models of hard nanoplates for (b) regular triangle, (c) regular square, (d) regular hexagon, (e) circle and (f) rod; (b)– (f) a fishnet-like network for the elastic surface of shells. Here bond lengths as well as monomer radii are also shown.

We enforce the elastic surface connectivity by linking adjacent beads via a harmonic spring potential[6]

where K = 300kBT/σ 2 is the spring constant, and r0 = 1.23σ is the equilibrium bond distance.

The bending rigidity of the elastic surface is modeled by a dihedral potential between adjacent triangles[6, 23, 24]

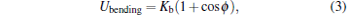where ϕ is the dihedral angle between opposite vertices of any two triangles sharing an edge, and Kb is the bending energy.

The nanoplates are composed of Nn monomers with diameter σ C, which are frozen into rigid-like bodies via the harmonic potential introduced in Eq.  (2) with , and the dihedral potential given in Eq.  (3) with b → Kb and θ → ϕ , where θ is the bond angle between two neighboring bonds. Detailed models of the hard nanoplates are shown in Fig.  1(b). The parameters are σ C = 4σ except that σ C = 6σ for the rods, K′ = 1000kBT/σ 2, , and b = 10000kBT to minimize possible deformation of the hard plates. For regular triangle (Nn = 15) and hexagon (Nn = 19), monomers are arranged on a two-dimensional hexagonal lattice; for regular square (Nn = 25), monomers are arranged on a two-dimensional simple cubic (SC) lattice, while for rods, monomers are connected by Nn monomers into a 1D “ stick” . In order to maintain stability, the neighboring monomers are partially overlapped. Meanwhile, monomers between any two different nanoplates interact with each other via the L– J potential described in Eq.  (1), and the plate– plate interaction is short-ranged repulsive.

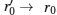
The generic binding of the monomer of nanoplates to the elastic shell is described by a Morse potential[23, 24]

where r is the center-to-center distance between a nanoplate monomer and a surface monomer, D0 = 8.0kBT is the binding energy, rM = 2.5σ is the monomer-bead contact distance, and α = 1.25/σ . Our aim of this paper is to investigate the self-assembly of nanoplates on an elastic shell, strong attractive interactions have to be considered. For a very weak binding energy, there is almost no interaction between the nanoplates and the shell, and the nanoplates are located randomly in the box, known as the gas phase.[25] At a moderate binding energy, the nanoplates are uniformly adsorbed on the shell, and there are no self-assembly structures for nanoplates.[25] Although a weak or moderate binding energy has an important influence in the self-assembly behavior, there are no self-assembly structures for nanoplates at a weak or moderate binding energy. Therefore, only at a large enough binding energy, one can observe the driven self-assembly behaviors for nanoplates on elastic shells.

We employ the LAMMPS molecular dynamics package[35] with a Nose– Hoover thermostat[36, 37] in the NVT ensemble to study the driven self-assembly behavior of nanoplates on soft elastic shells. The temperature of the system is set to T = 1.0, the time step is τ = 0.001τ 0, and each simulation runs at least 2 × 107 steps in the periodic box 200σ × 200σ × 200σ . Meanwhile, the number of the surface monomers is Ns = 10242, and the radius of elastic shell is R = 32.5σ .

3. Results and discussion
3.1. Ordered structures of adsorbed hard nanoplates on elastic shells

A dimensionless parameter known as the Fö ppl– von Kà rmà n number γ = YR2/Kb can well describe the surface tension of elastic shells, where Y is the Young’ s modulus of the elastic shell and Kb is the bending rigidity defined in the continuum theory of elasticity.[38] Since the Young’ s modulus of the elastic shell Y and the shell radius R in our model are constant, the Fö ppl– von Kà rmà n number is simplified as γ ∝ 1/Kb. Therefore, the elastic property of the shell can be illustrated by the bending energy Kb. The driven self-assembly behaviors of hard nanoplates on soft elastic shells depend on the shape of hard nanoplates, the bending energy of elastic shells, and the number of hard nanoplates. A series of simulations for various shapes of nanoplates (regular triangle, square, regular hexagon, circle, and short rod with 4 monomers) with different nanoplate numbers N = 36, 48, and 60 are carried out, and the results are shown in Fig.  2. For the elastic shell with a moderate bending energy (Kb = 10000), the nanoplates aggregate in the flat regions, and the ordered structures of aggregation nanoplates are observed. The structure of each aggregated cluster is governed by the shape of nanoplates and the number of nanoplates in the system, while the total number of the aggregation clusters is always a constant of 12. According to previous work, for an elastic shell with a weak bending energy of Kb = 1000, there are a series of peaks on the Θ Φ surface in the spherical coordinate system, and the area of each peak and the distance between any two neighboring peaks are identical, and the number of peaks is twelve.[23, 25] There are twelve required five-fold disclinations due to the topology of the discrete spherical model, which has been proved in previous works.[39, 40] However, for the elastic shell with a relatively high bending energy of Kb = 10000, which is larger than the stretching energy, [6] the shape of the elastic shell is mainly determined by the bending energy and the radius distributions of the elastic shell on the Θ Φ surface. The Θ Φ surface of the shell with Kb = 10000 is completely different from that of the shell with Kb = 1000.[23] The peak regions in the radius distributions of the elastic shell with a weak bending energy become the valley regions for the elastic shell with a high bending energy.[23] The aggregation clusters of hard nanoplates are distributed among these 12 regions. For nanoplates with the fixed shape, the aggregation structure depends mainly on the total number of nanoplates in the simulation system. For example, for square nanoplates, there are three different aggregation structures for N = 36, in which two, three, and four squares are aggregated, while six, seven, and eight squares are aggregated for N = 60.

Fig.  2. Simulation snapshots of representative aggregation structures for regular triangle, regular square, regular hexagon, circle, and rod with various numbers of hard nanoplates N = 36, 48, and 60, respectively. Here the bending energy of the elastic shell is Kb = 10000, and N is the total number of hard nanoplates.

Detailed descriptions of the ordered structures are given in Fig.  3. For each n, there are various aggregation structures, where n is the number of nanoplates in one aggregation cluster. For a large n, there are different conformations for a given n, and the percentage of different conformations is shown in the top right corner of the snapshots. Hard nanoplates are aggregated on elastic shells on the basis of the minimization of the second moment of the mass distribution.[41, 42] As there exist some plate regions in the radius distributions on the Θ Φ surface, [23] hard nanoplates are aggregated on these regions as compactly as possible. For regular triangles, the aggregated structures are not perfect and the triangle edges are not parallel to each other completely for n = 6, 7. However, regular triangles are aggregated in a perfect manner for n = 2, 3, and 4. For regular squares, most of the squares are in the parallel arrangement, and some squares can move randomly along the parallel edges. For regular hexagons and circles, the perfectly aggregated structures are shown in Fig.  3.

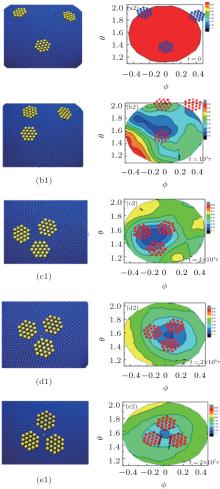
Fig.  3. Some representative conformations of hard nanoplates on the soft elastic shells with various n at Kb = 10000. Here n is the number of nanoplates in one aggregation cluster, and the percentage of different configurations is shown in the top right corner of the snapshot.

To understand the mechanism of forming the ordered aggregation structures, we choose the regular hexagons as an example to explore the simulation process of a system with a constant bending energy Kb = 10000, and the results are shown in Fig.  4. Initially, the nanoplates are placed randomly in the simulation box and away from the elastic shell. The radius distribution on the Θ Φ surface for the elastic shell is uniform, and the radial distances of the surface monomers are almost close to 32.5σ for all surface monomers. After a short simulation time, the nanoplates are adsorbed on the elastic shell under the effects of binding energy, which makes the shells fluctuate drastically and leads to a decrease of the mean radius of elastic shells from 〈 R〉 = 32.5 at t = 0 to 〈 R〉 = 31.4 at t = 104τ due to the compression of adsorbed nanoplates on the elastic shells. The surface tension of the elastic shell can drive the nanoplates to move towards the flat regions of the elastic shells and these movements can minimize the total system energy, see Fig.  4(c2). After a long period of equilibrium, ordered structures of nanoplates are finally formed, in which the adjacent hexagon edges are parallel to each other because this parallel arrangement can maximize the local packing fraction, see Fig.  4(e2). Therefore, we can conclude that the driven self-assembly behavior of the hard nanoplates consists of two stages: firstly, nanoplates are adsorbed onto the shell randomly and then accumulate towards the center of the flat region driven by the surface tension of the elastic shell; secondly, the nanoplates rearrange on the basis of the maximization of local packing fraction. To explain the process of self-assembly behavior more intuitively, we draw schematic illustrations about the aggregation mechanism in Fig.  5. When nanoplates are adsorbed on the surface of the elastic shell, the shell surface has an obvious deformation and there are some valley regions on the surface of elastic shells. If the nanoplates are adsorbed on these valley regions, the nanoplates move towards the center of the valley regions, see Fig.  5(a). After the nanoplates are driven by the surface tension, the nanoplates approach each other, and they are arranged on the basis of maximization of local packing fraction and the parallel arrangement of nanoplate edges, see Fig.  5(b). This is the mechanism of forming ordered structures for nanoplates on elastic shells.

Fig.  4. Left: Snapshots at different simulation times suggesting that the combination of nanoplate shape and surface tension of soft shell directs the formation of an ordered structure for regular hexagon. Right: The corresponding radius distributions of elastic shells at different simulation times.

Fig.  5. Schematic illustrations indicating that the driven self-assembly behaviors of the hard nanoplates consist of two stages: (a) the nanoplates are adsorbed onto the shell randomly and then accumulate towards the center of the flat region driven by surface tension of the elastic shell; (b) the nanoplates rearrange on the basis of the maximization of local packing fraction.

In order to explore whether nanoplates are driven to flat regions or flat regions are induced by aggregated plates in more detail, we calculate the energy distribution of the elastic shell for N = 0, 12, and 36, as shown in Fig.  6. It can be concluded that the adsorption behaviors depend mainly on the bending energy of the elastic shells because all the regular hexagons are located at the regions with the low bending energies. The nanoplates are aggregated on the basis of the minimization of the second moment of the mass distribution.[41, 42] The driving force for nanoplates to be aggregated comes from the surface tension of elastic shells because there are no interactions between the nanoplates.

Fig.  6. The energy distribution of the soft elastic shell (first row) and the corresponding snapshots (second row) for regular hexagons with N = 0, 12, and 36.

3.2. Effects of bending energy on driven self-assembly behaviors of adsorbed nanoplates

In order to investigate the effects of bending energy Kb on the driven self-assembly behaviors of nanoplates on elastic shells, a series of simulations with various bending energies for Kb = 100, 10000, and 5 × 105 are performed, and the results are shown in Fig.  7. For the elastic shell with a very low bending energy of Kb = 100, it is collapsed completely no matter what shape the nanoplate is. For the elastic shell with a moderate bending energy of Kb = 10000, the aggregation structures of nanoplates are distributed among the relatively flat regions. For the elastic shell with a very high bending energy (such as 5 × 105), it needs a very large energy for the shells to deform a little, and the adsorption behavior of nanoplates on the shells is isotropic. The driven self-assembly process cannot occur for Kb = 5 × 105, and no aggregation cluster for nanoplates can be formed, see Fig.  7(c). In fact, the adsorption behaviors of nanoplates on elastic shells are quasi-dimensional. In order to compare the different adsorption behaviors of nanoplates on elastic shells with those on a two-dimensional (2D) surface, we also simulate the adsorption processes of nanoplates on two-dimensional surfaces, and the results are also shown in Fig.  7(d). The nanoplates are adsorbed randomly on a two-dimensional surface, and no aggregation clusters are formed. Therefore, the adsorption behaviors of nanoplates on soft elastic shells are completely different from those on two-dimensional surfaces.

Fig.  7. Evolutions of hard nanoplates on soft elastic shells at various bending energies with Kb = 100 (A), 10000 (B), and 5 × 105 (C) for regular triangle, square, hexagon, and circle, respectively. The adsorption behaviors of hard nanoplates on two-dimensional (2D) planes are shown in panel (D) for comparison. Here N = 48.

To gain insight into the physical origin of different aggregation behaviors for nanoplates on elastic shells with different bending energies, we plot three possible schematic illustrations in Fig.  8. For a very soft elastic shell, the shell is so soft that the nanoplates can affect the shapes of shells seriously, and the collapsed structures are observed, see Fig.  8(a). For the elastic shell with moderate bending energy, as there are some flat regions on the elastic surface, several nanoplates can be aggregated on the plate regions of the elastic surface. As the shell surface is relatively soft, the elastic shell can deform a little according to the interactions between the nanoplates and the elastic shells. However, for elastic shell with a very high bending energy, the attraction ability of hard shell for nanoplates may decrease because some monomers for nanoplates exceed the attraction ranges, see the inset of Fig.  8(c). In fact, the adsorption abilities of nanoplates on the hard shells are weaker than those on the elastic shells at the same binding energy. Meanwhile, the adsorption process onto the soft elastic shells for nanoplates includes two stages: i) the nanoplates are adsorbed on the shells randomly; ii) the nanoplates are rearranged on the basis of the maximization of local packing fraction. However, for the very hard shells, the adsorption process of the nanoplates on the hard shells only consists of the first stage. Therefore, the effects of bending energy on driven self-assembly behaviors of adsorbed nanoplates are obvious, and the adsorption behaviors of nanoplates on elastic shells have their distinguishing features.

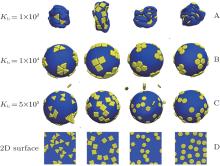
Fig.  8. Schematic illustrations showing the effects of bending energy on the driven self-assembly behaviors of regular triangle on soft elastic shells. A: Nanoplates are located randomly in the simulation box; B: nanoplates are adsorbed onto the shell; C: the whole system reaches equilibrium. Different attractive abilities of soft elastic shells and hard shells for regular triangles are given in the top right corner, and the cross means that the shell monomer and the regular triangle monomer are hardly attractive to each other.

3.3. Deformations of elastic shell controlled by adsorbed rods

Rods have a special property of additional orientation entropy, which is different from the normal nanoplates. Previous simulations on the aggregation behaviors of short and long rods on soft elastic shells have found that the aggregation structure of the rods is relevant to the bending energy of the elastic shell.[24] However, the detailed discussion about the dependences of rod lengths and the number of rods has not been given yet. Figure  9 shows the phase diagram in the Nb– N plane. Here Nb is the number of monomers in a rod, and N is the number of rods in our simulation system. For short rods (i.e., Nb ≤ 9), the rods are aggregated and can form 12 clusters in the 12 flat regions as mentioned above, while the shell maintains its original shape as a sphere (see phase A in Fig.  9). When the rod length increases, due to the parallel arrangement of the rods, some flat regions can no longer hold enough rods, so that some clusters tend to connect to each other and form some larger clusters, and a transition from A phase to B phase occurs. B phase consists of 3 large clusters and several small clusters. Three large clusters pinch the shell and the shell is deformed into a tricorn. Some small clusters are aggregated in the empty flat regions, and the number of small clusters decreases with the increase of rod length. The number of large clusters is 3, and the numbers of small clusters are 6, 3, and 1 in Figs.  9(b1), 9(b2), and 9(b3). For simplicity, we group them into phase B. For long rods (Nb ≥ 15) with N = 36, the rods can squeeze the shell into an ellipsoid, and form a large circular cluster surrounding the shell surface (see phase D in Fig.  9). For a sufficient number of long rods, such as Nb ≥ 12 and N ≥ 54, or Nb ≥ 15 and N = 48, a two-cluster phase is observed, in which the rods nearly cover the entire surface of the shell, and the shell deforms like a pillow (see phase E in Fig.  9). If the number of long rods is greater than 68, although the adsorbed rods are locally parallel to each other, they have no space to adjust their positions on the shell, and the shell deforms irregularly (see phase C in Fig.  9).

Fig.  9. Phase diagram of aggregation structures for rods on elastic shell in the plane of rod length Nb and the number of rods N. There are three main phases: 12-cluster (A, black square), (3+ n)-cluster (B, red circle), irregular (C, blue triangle). Additionally, two possible phases are hidden in the above phases and labeled by dashed lines, and they are 2-cluster (D), 1-cluster (E). Typical snapshots are: A phase with N = 66, Nb = 5; B phase with N = 66, Nb = 6 B(1); N = 66, Nb = 9 B(2); N = 42, Nb = 15 B(3); C phase with N = 78, Nb = 20; D phase with N = 48, Nb = 15; and E phase N = 36, Nb = 18.

We calculate the surface asphericity  A of the shell, which is defined as[6, 23]

where Ri is the radial distance of the surface monomer i, and 〈 R〉 is the mean radius of the elastic shell. Figure  10 shows that the asphericity of the shell increases slowly for short adsorbed rods with Nb ≤ 8, followed by a rapid growth for the moderate lengths of rods with 9 ≤ Nb ≤ 15, and slows down a little with Nb ≥ 16. One notes that for long rods, the larger number of rods the system consists of, the smaller the asphericity A is. For short rods, the elastic shell does not undergo large deformations to ensure the rod– shell interactions to minimize total energy, so that the original spherical shape of the shell is well maintained. When the rod length increases, the binding energy causes remarkable deformations of the shell, followed by the self-assembly behaviors of the long rods. Governed by the orientational entropy, these rods rearrange themselves and affect the shape of the shells in return. Finally, one can obtain various shapes of shells such as a tricorn, an ellipsoid, or a pillow-like shape. However, for a number of long rods in the system, the adsorption behaviors of the rods are isotropic, and there is not enough space to adjust their positions. The shell has to accommodate and deform irregularly, so we can observe a slight decay on the curve for large Nb, see Fig.  10. The potential interactions dominate the deformation of the elastic shell and the driven self-assembly behavior of rods depends on the competition between the orientational entropy of rods and the potential interactions of elastic shell.

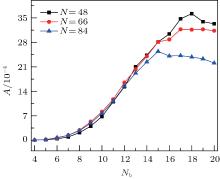Fig.  10. The surface asphericity of elastic shell A as a function of rod length Nb for various numbers of nanorods.

4. Conclusions

In this paper, we investigate the driven self-assembly behaviors of hard nanoplates on soft elastic shells by employing a molecular dynamics simulation method. The adsorption behaviors of nanoplates on elastic shell depend mainly on the bending energy of the elastic shell. The driven self-assembly structures of adsorbed nanoplates are determined by the minimization of the second moment of the mass distribution. For shells with a low bending energy, the elastic shells are completely collapsed. For shells with a moderate bending energy, ordered structures are formed for various shapes of hard nanoplates. For shells with a high bending energy, the nanoplates are adsorbed randomly on the shell. The shell is hardly deformed for triangles, squares, hexagons, circles, and short rods, and has a remarkable deformation for long rods because of the large binding energy caused by the rod– shell interactions. One can observe various shapes of shells such as a sphere, a tricorn, an ellipsoid, and a pillow-like shape by adjusting the number of rods and the rod lengths. These investigations can help us understand the complexity of driven self-assembly of hard nanoplates on elastic shells and can hold promise for the applications in material designing as well as controlling the shape of shells in the micrometer range or smaller sizes.

Reference
1 Zhang S M, Greefield M A, Mata A, Palmer L C, Bitton R, Mantei J R, Aparicio C, Olvera de Cruz M and Stupp S I 2010 Nat. Mater. 9 594 DOI:10.1038/nmat2778 [Cited within:1]
2 Vernizzi G, Sknepnek R and Olvera de Cruz M 2011 Proc. Natl. Acad. Sci. USA 108 4292 DOI:10.1073/pnas.1012872108 [Cited within:1]
3 Pàmies J C and Cacciuto A 2011 Phys. Rev. Lett. 106 045702 DOI:10.1103/PhysRevLett.106.045702 [Cited within:2]
4 Ŝarić A and Cacciuto A 2012 Phys. Rev. Lett. 108 118101 DOI:10.1103/PhysRevLett.108.118101 [Cited within:1]
5 Ŝarić A and Cacciuto A 2011 Soft Matter 7 8324 DOI:10.1039/c1sm05773a [Cited within:2]
6 Ŝarić A and Cacciuto A 2011 Soft Matter 7 1874 DOI:10.1039/C0SM01143F [Cited within:7]
7 Jha P K, Kuzovkov V, Grzybowski B A and Olvera de Cruz M 2012 Soft Matter 8 227 DOI:10.1039/C1SM06662E [Cited within:1]
8 Velichko Y S and Olvera de Cruz M 2006 J. Chem. Phys. 124 214705 DOI:10.1063/1.2205854 [Cited within:1]
9 Alberts B, Johnson A, Lewis J, Raff M, Roberts K and Wzlter P 2008 Molecular Biology of the Cell New York Garland Science [Cited within:1]
10 Rothemund P W K 2006 Nature 440 297 DOI:10.1038/nature04586 [Cited within:1]
11 King N P, Sheffler W, Sawaya M R, Vollmar B S, Sumida J P, Andre I, Gonen T, Yeates T O and Baker D 2012 Science 336 1171 DOI:10.1126/science.1219364 [Cited within:1]
12 Hartgerink J D, Beniash E and Stupp S I 2001 Science 294 1684 DOI:10.1126/science.1063187 [Cited within:2]
13 Nykypanchuk D, Maye M M, Lelie D V D and Gang O 2008 Nature 451 549 DOI:10.1038/nature06560 [Cited within:1]
14 Brown F L H 2008 Annu. Rev. Phys. Chem. 59 685 DOI:10.1146/annurev.physchem.59.032607.093550 [Cited within:1]
15 Discher D E, Janmey P and Wang Y 2005 Science 310 1139 DOI:10.1126/science.1116995 [Cited within:1]
16 Engler A, Bacakova L, Newman C, Hategan A, Griffin M and Discher D 2004 Biophys. J. 86 617 DOI:10.1016/S0006-3495(04)74140-5 [Cited within:1]
17 Georges P C and Janmey P A 2005 J. Appl. Physiol. 98 1547 DOI:10.1152/japplphysiol.01121.2004 [Cited within:1]
18 Huang J, Juszkiewicz M, de Jeu W H, Cerda E, Emrick T, Menon N and Russell T P 2007 Science 317 650 DOI:10.1126/science.1144616 [Cited within:1]
19 Stafford C M, Harrison C, Beers K L, Karim A, Amis E J, Vanland ingham M R, Kim H C, Volksen W, Miller R D and Simony E E 2004 Nat. Mater. 3 545 DOI:10.1038/nmat1175 [Cited within:1]
20 Schweikart A, Fortini A, Wittemann A, Schmidt M and Fery A 2010 Soft Matter 6 5860 DOI:10.1039/c0sm00744g [Cited within:1]
21 Boncheva M and Whitesides G M 2005 MRS Bull 30 736 DOI:10.1557/mrs2005.208 [Cited within:1]
22 Xiong X and Hanein Y 2003 J. Microelectromech. Syst. 12 117 DOI:10.1109/JMEMS.2003.809964 [Cited within:1]
23 Zhang D, Chai A H, Wen X H, He L L, Zhang L X and Liang H J 2012 Soft Matter 8 2152 DOI:10.1039/c1sm06653f [Cited within:9]
24 Wen X H, Zhang D, Chai A H, He L L, Ran S Y and Zhang L X 2012 Soft Matter 8 6706 DOI:10.1039/c2sm25477h [Cited within:4]
25 Jiang Y W, Zhang D, Jin Y K and Zhang L X 2013 J. Chem. Phys. 138 214901 DOI:10.1063/1.4807592 [Cited within:4]
26 Zhang S Z, Kou X S, Yang Z, Shi Q H, Stucky G D, Sun L D, Wang J F and Yan C H 2007 Chem. Commun. 18 1816 [Cited within:1]
27 Shevchenko E V, Talapin D V, Kotov N A, Brien S O and Murray C B 2006 Nature 439 55 DOI:10.1038/nature04414 [Cited within:1]
28 Yethiraj A and Van Blaaderen A 2003 Nature 421 513 DOI:10.1038/nature01328 [Cited within:1]
29 Chen Q, Bae S C and Granick S 2011 Nature 469 381 DOI:10.1038/nature09713 [Cited within:1]
30 Ye X C, Chen J, Engel M, Millan J A, Li W B, Qi L, Xing G Z, Collins J E, Kagan C R, Li J, Glotzer S C and Murray C B 2013 Nat. Chem. 5 466 DOI:10.1038/nchem.1651 [Cited within:2]
31 Zhang Y W, Sun X, Si R, You L PN and Yan C H 2005 J. Am. Chem. Soc. 127 3260 DOI:10.1021/ja042801y [Cited within:1]
32 Wang F, Han Y, Lim C S, Lu Y, Wang J, Xu J, Chen H, Hong M and Liu X 2010 Nature 463 1061 DOI:10.1038/nature08777 [Cited within:1]
33 Hsu C W and Chen Y L 2010 J. Chem. Phys. 133 034906 DOI:10.1063/1.3457156 [Cited within:1]
34 Lidmar J, Mirny L and Nelson D R 2003 Phys. Rev. E 68 051910 DOI:10.1103/PhysRevE.68.051910 [Cited within:1]
35 Plimpton S J 1995 J. Comput. Phys. 117 1 [Cited within:1]
36 Nose S 1984 J. Chem. Phys. 81 511 DOI:10.1063/1.447334 [Cited within:1]
37 Hoover W G 1985 Phys. Rev. A 31 1695 DOI:10.1103/PhysRevA.31.1695 [Cited within:1]
38 Land au L D and Lifshitz E M 1970 Theory of Elasticity New York Pergamob [Cited within:1]
39 Bowick M J and Sknepnek R 2013 Soft Matter 9 8088 DOI:10.1039/c3sm51729b [Cited within:1]
40 Funkhouser C M, Sknepnek R and Olvera de Cruz M 2013 Soft Matter 9 60 DOI:10.1039/C2SM26607E [Cited within:1]
41 Manoharam V N, Elsesser M T and Pine D J 2003 Science 301 483 DOI:10.1126/science.1086189 [Cited within:2]
42 Graham R L and Sloane N J A 1990 Discrete Comput. Geom. 5 1 DOI:10.1007/BF02187775 [Cited within:2]