†Corresponding author. E-mail: liutq@dlut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 50876015).
Whether droplets transit from the Cassie to the Wenzel state (C–W) on a textured surface is the touchstone that the superhydrophobicity of the surface is still maintained. However, the C–W transition mechanism, especially the spontaneous transition of small droplets, is still not very clear to date. The interface free energy gradient of a small droplet is firstly proposed and derived as the driving force for its C–W evolution in this study based on the energy and gradient analysis. Then the physical and mathematical model of the C–W transition is found after the C–W driving force or transition pressure, the resistance, and the parameters of the meniscus beneath the droplet are formulated. The results show that the micro/nano structural parameters significantly affect the C–W driving force and resistance. The smaller the pillar diameter and pitch, the minor the C–W transition pressure, and the larger the resistance. Consequently, the C–W transition is difficult to be completed for the droplets on nano-textured surfaces. Meanwhile if the posts are too short, the front of the curved liquid–air interface below the droplet will touch the structural substrate easily even though the three phase contact line (TPCL) has not depinned. When the posts are high enough, the TPCL beneath the drop must move firstly before the meniscus can reach the substrate. As a result, the droplet on a textured surface with short pillars is easy to complete its C–W evolution. On the other hand, the smaller the droplet, the easier the C–W shift, since the transition pressure becomes larger, which well explains why an evaporating drop will collapse spontaneously from composite to Wenzel state. Besides, both intrinsic and advancing contact angles affect the C–W transition as well. The greater the two angles, the harder the C–W transition. In the end, the C–W transition parameters and the critical conditions measured in literatures are calculated and compared, and the calculations accord well with the experimental results.
Cassie and Wenzel states are two typical wetting statuses of droplets on rough surfaces. Droplets show large contact angles and small contact angle hystereses, i.e., superhydrophobic properties, only when they exist in the Cassie state. However, when droplets appear in the Wenzel state, the contact angle hysteresis is substantial, and the surface loses its superhydrophobicity. Therefore, the conditions and mechanism of droplet transition from Cassie to Wenzel state (C– W) on textured surfaces are the key research contents of superhydrophobic materials.
The C– W transition of droplets may result from two different causes, external driving and self evolution. There are several methods to exert a force on a droplet for its C– W shift, such as the compression between two superhydrophobicplates, [1] the static pressure or hydraulics pressure, [2– 4] the impact force of droplet landing from a high place, [5, 6] and the static electricity wetting force.[7– 10] It is easy to understand the C– W mechanism of this type. When an external force is larger than the resistance of three phase contact line (TPCL) depinning below a droplet or when the meniscus touches the texture substrate caused by the force, the droplet begins the C– W transition. The so-called self evolution on the other hand means a C– W transition in which a droplet on a structural surface is not affected by any external force, but only by the interaction between the droplet and the textured surface. For example, an evaporating droplet on a rough surface will convert from composite state to Wenzel state spontaneously when its volume decreases to a critical value.[10– 14] Until recently, however, this mechanism of the spontaneous transition is still unclear. There are a few conflicted interpretations, including the Laplace pressure inside droplets as the transition driving force, [1, 5, 15] the external force overcoming the Laplace pressure, [16] the gravity of droplets as the driving force, [17– 19] and unknown liquid pressure, [20] etc. Therefore, it is necessary to clarify the mechanism of droplet spontaneous C– W transition.
Most experiments are performed by recording the abrupt changes of apparent contact angles, [13, 21, 22] droplet radii, [13] or base areas[11] of the droplets before and after the C– W transition. These results could only reflect the critical conditions of C– W conversion, such as structural parameters and droplet size, but cannot provide the shape changing of the liquid– air interface beneath the droplet and the whole dynamic process of the wetting state transformation. Tsai et al.[14] and Sbragaglia et al.[23] recorded the wetting evolution process of droplets on transparent substrates with microscope and high-speed camera, showing the shape at the initial wetting point and the expanding area beneath the droplet, as well as the moving speed of TPCL. However, they did not present how the bottom of a Cassie state droplet was initially wetted, and did not consider the driving force of the C– W transition. On the other hand, Moulinet et al.[24] and Antonini et al.[25] respectively presented a reflection interference contrast microscopy and an x-ray radiography based visualization method to directly observe the penetration process of Cassie– Baxter to Wenzel state transition during drop evaporation. Meanwhile, Papadopoulos et al.[12] first revealed the dynamic process during the C– W transition of evaporating droplets by laser confocal microscopy. With the evaporation of a droplet, the curvature of the water– air interface beneath the drop increased. The C– W transition was accomplished through two pathways, i.e., sagging and TPCL depinning for short and high posts, respectively, which was also proposed by others.[18, 26, 27] Although Papadopoulos’ s study did not clearly propose the driving force for the C– W spontaneous transition, their results provided a valuable reference for further theoretical study of the C– W transition.
Although there are many models to calculate the C– W transition, [4, 5, 15, 16, 18, 20, 24– 31] and the C– W driving forces accepted in these models include external force, [4, 16, 28] gravity, [18, 27, 29] Laplace pressure, [5, 24, 25, 27, 30] impalement pressure[31] inside the droplet, unknown hydraulic pressure, [20] and droplet surface energy, [26, 29] none of them is relevant to the true driving force for the spontaneous C– W transition of small droplets. In fact, the effect of gravity could be ignored for a droplet if its size is smaller than the capillary length.[12] And the Laplace pressure on the meniscus below a droplet is a kind of resistance to impede TPCL depinning, [8, 16] not the driving force. Moreover, almost all of these published models could not reflect and explain the effect of drop-size reduction on the spontaneous C– W transition of small droplets during evaporation. Therefore, it indeed needs to clarify the real driving force of the C– W spontaneous transition, so that the curved liquid– air interface beneath a composite droplet and TPCL depinning etc. can be solved according to the relationship between the driving force and the resistance.
We propose and derive a novel driving force of the C– W spontaneous transition, the interface free energy gradient (IFEG) of a droplet. It is this IFEG that makes the liquid– air interface below the droplet bend and the TPCL there depin when the IFEG is larger than the wetting resistance. We also propose that whether the TPCL beneath the droplet continues shifting after depinning does not depend on whether the IFEG is greater than the resistance, but relies on whether the dynamic energy of the droplet TPCL moving forward is larger than zero.
The liquid– air interface beneath a composite droplet sitting on a structural surface tends to bend under the action of the C– W transition driving force, as shown in Fig. 1. When the meniscus touches the structural substrate, the C– W transition will be completed.[12, 18, 24, 26, 27] Below, the driving force, the resistance of the C– W transition, and the relevant parameters describing the meniscus, as well as the criterion whether the TPCL beneath a droplet continues shifting after depinning are analyzed respectively.
When the size of a droplet is smaller than the capillary length, the gravity acting on the droplet could be ignored.[12] In fact, all the experimental results indicated that the smaller a droplet is, the easier its C– W transition, which means that gravity is not the primary cause. Additionally, there are no other obvious external forces, such as the hydraulic pressure, acting on a small droplet during its evaporation. Then we propose here that the IFEG possessed by a droplet is the driving force to complete its C– W transition, as shown in Fig. 2(a). This is quite similar to the case that a solid object on an inclined wall slides along the surface under the action of its potential energy gradient (gravity) as shown in Fig. 2(b). Just because the energy gradient is a kind of driving force, [32, 33] the object can move from a high energy position to a lower one. For the object in Fig. 2(b), its initial potential energy is Ep0, and its initial velocity is zero. If the friction along the surface is FF, the energy of this object at any position x is (internal energy is not included)
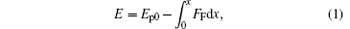 |
where 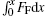
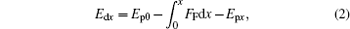 |
where Edx and Epx are the local dynamic and potential energies at position x, respectively. If differentiating each term in the above equation to x, we can find
 |
where − dEpx/dx indicates the potential energy gradient of the object from a high position to a lower one, i.e., the gravity or the driving force making the object slide. It is thus clear that the potential energy gradient of an object is the driving force for its spontaneous movement from high energy position to lower one. Besides, dEdx/dx in Eq. (3) is the dynamic energy gradient, namely, the inertial force of the object. Therefore, equation (3) is just the same as the one of Newtonian’ s second law.
Especially, at the initial position x = 0, the critical condition for the object starting to move is
 |
For the inclined surface with slope decreasing continuously shown in Fig. 2(b), the potential energy gradient of the object may become equal to or less than the friction force when the object arrives at a certain position x0, i.e., − dEpx/ dx| x≥ x0 ≤ FF. But the object will not stop at this location because it already possesses a certain speed or dynamic energy. Only after the object continuously moves forward for a certain distance with its speed declining sustainedly until zero, it will stop. Therefore, the criterion of the object stopping moving forward is not the driving force equal to or less than the resistance, but is its dynamic energy or speed equal to zero. Namely, the criterion is
 |
The process of an initial Cassie droplet transiting to the Wenzel state on a textured surface is very similar to that of the above case. The initial Cassie droplet has a certain interface free energy (IFE) which corresponds to the potential energy of the above object. If the TPCL below an initial Cassie droplet is able to move downwards, its IFEG, − dEx/dx, must be greater than the resistance preventing the TPCL to depin. Quite similar to Eq. (4), the critical condition of the TPCL below an initial Cassie droplet starting to depin is
 |
where x is the distance of the TPCL moving downward, and Ex is the IFE of the droplet, which is derived as follows.
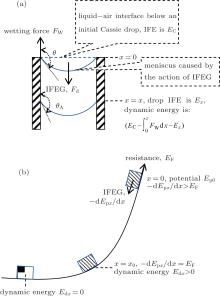 | Fig. 2. Schematics of (a) bending and depinning of droplet base TPCL acted by its IFEG and (b) a solid object on an inclined surface acted by its potential energy gradient. |
For a composite droplet, when its base TPCL shifts to position x along posts (Fig. 2(a)), its IFE can be expressed as[22]
 |
where Acap and Ab are the sphere cap and the base area of the droplet, respectively; σ LG, σ SG, and σ SL are the liquid– gas, solid– gas, and solid– liquid interface tensions, respectively; f and r are the solid area fraction and the Wenzel roughness factor of the structural surface, respectively; H is the height of the pillars; and Atotal is a fixed surface area to calculate the IFE of the droplet.[22] The IFE of the composite droplet in Eq. (7) covers all interfacial energy in the selected area including the drop.
After simplification, equation (7) becomes
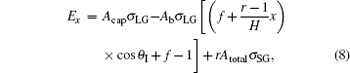 |
where θ I is the intrinsic contact angle determined by the Young equation
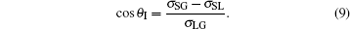 |
And the expressions of Acap and Ab are
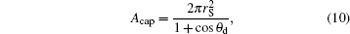 |
 |
where θ d is the apparent contact angle, which is determined by the following formula when the volume of the droplet is
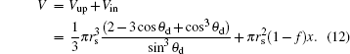 |
Here, the whole drop volume V is divided into two parts, the segment volume above posts Vup and the volume into structures Vin.
Then the final equation of the droplet IFE is
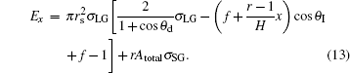 |
For cylindrical posts, the Wenzel roughness factor r and the solid area fraction f in the equation are given as
 |
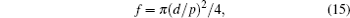 |
where d, H, and p are the diameter, the height, and the pitch of the pillars, respectively.
Furthermore, the IFEG, − dEx/dx, in Eq. (6) is just the driving force of the droplet spontaneous C– W transition, which can be found by the relevant partial differentiations with Eqs. (12) and (13),
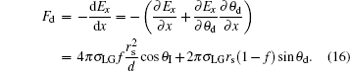 |
The validity and the detailed derivation process of this equation are shown in the supplementary information.
It should be pointed out that there may be three types of modes for the TPCL below a droplet to shift downward. The first one is by decreasing the apparent contact angle of the droplet while the base radius unchanging; the second mode is by reducing the base radius while the contact angle kept constant; the third one is by changing both the contact angle and base radius. It can be proved that the TPCL moves downward only in the first mode, as described in the supplementary information and Eq. (16).
Finally, FW in Eq. (6) is the resistance preventing the TPCL moving down to wet the sides of the posts, which is explained as follows.
The TPCL depinning below a droplet is usually the main way of C– W transition. And the phenomenon is similar to a Wilhelmy plate moving into a liquid. Both processes are the wetting procedures of solid surfaces. A hydrophobic surface is difficult to be wetted by water so that the TPCL is difficult to move forward as being acted by a resistance. Only after the contact angle at the TPCL becomes the advancing angle, the TPCL depins. At this time, the driving force to push the TPCL shifting is equal to the wetting force on the TPCL. Therefore, the wetting force or capillary force on the TPCL on a hydrophobic surface is the resistance preventing the TPCL depinning. Similar to the calculation of the wetting force on a hydrophobic Wilhelmy plate, [34] the wetting force or resistance on the TPCL beneath a droplet on hydrophobic posts can be expressed as
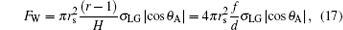 |
where θ A is the advancing contact angle when the TPCL moves forward (Fig. 2).[25, 35– 37] The physical meaning of Eq. (17) is similar to that of the capillary force expressed in literatures.[24, 25]
When the liquid– air interface below a droplet becomes bending under the action of IFEG, the additional pressure[38] acting on the meniscus resulted from the surface tension will be generated to resist the bending, i.e., to resist the enlargement of the liquid– air interface. The resultant of this additional pressure is just opposite to the C– W driving force, so it is the resistance against the bending of the liquid– air interface. It can be proved that the resistance equals to the component of the surface tension acting on the all TPCL beneath the droplet,
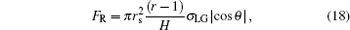 |
where θ is the contact angle between the liquid– air interface and the side wall of the pillars below the droplet (Fig. 2). By comparing Eq. (17) with Eq. (18), it is clear that FR in Eq. (18) is also the resistance preventing the TPCL moving when the liquid– air interface bends to a certain degree, i.e., when the curvature of the meniscus becomes the maximum, θ and FR in Eq. (18) will respectively equal to θ A and FW in Eq. (17), and the TPCL will start to depin.
In order to exclude the effect of the bottom area of the droplet, the C– W transition driving force in Eq. (16) and the resistance in Eq. (17) are divided by the droplet bottom area, respectively. Thus the C– W transition pressure Pt and the transition resistance Rt are defined as
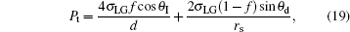 |
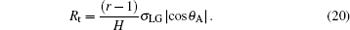 |
It needs to be pointed out that the C– W transition pressure defined by Eq. (19) is fundamentally different from the hydraulic pressure, [2, 3] since the latter is usually caused by gravity of a liquid or an external force acted on the liquid and it is generally relevant to the depth of liquid, while Pt in Eq. (19) does not have any relation with gravity or external forces. It is this Pt that causes small composite droplets to transit to the Wenzel state since Pt is inversely proportional to rs. Thus the phenomenon of C– W spontaneous transition of droplets during evaporation could be well explained with the pressure.
The C– W transition pressure Pt acting on a Cassie state droplet can be divided into the following three circumstances.
a) Pt ≤ 0, in this case there is no transition pressure acting on the droplet, and the droplet stays at the Cassie state without its bottom liquid– air interface bending. b) 0 < (1 – f)Pt ≤ Rt, in this case the droplet is affected by the pressure, and its bottom liquid– air interface is bending while the contact angle on the side wall of the posts is less than the advancing contact angle, so the TPCL is still pinned. The pressure acting on the droplet is balanced by the resistance shown in Eq. (18)
c) (1 – f)Pt > Rt, the TPCL depins in this situation.
For a certain Pt, the contact angle of the curved liquid– air interface can be firstly found according to Eq. (21), and then the other parameters of the meniscus can be calculated with the following relations:
 |
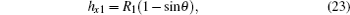 |
 |
In the above formulas, R1 and R2 are the two arc radii on the curved liquid– air interface beneath the droplet respectively locating between the two adjacent and diagonal pillars with a square array. And hx1 and hx2 are the bending depths of the above two arcs, respectively, as shown in Fig. 1.
For short posts, the meniscus below a droplet will sag and touch the structural substrate before the TPCL depins. While for high pillars, the TPCL begins to move after the liquid– air interface bends to maximum until the meniscus contacts the pillar base. Touching the texture substrate of the meniscus is used as the criterion for droplets completing the C– W transition for both short and high posts in this model,
 |
For short posts, x = 0; while for high pillars, x > 0.
For high posts, it is also necessary to judge whether the shifted TPCL beneath the composite droplet is able to continue to move forward until it touches the substrate of the textures. The judgment method is quite similar to that for the solid object to move forward sustainedly, as shown in Fig. 2(b) and Eq. (5). Now whether the “ dynamic” or the “ moving forward” energy of the composite droplet, when its base TPCL shifts to x, is greater than zero should be used as the criterion, namely,
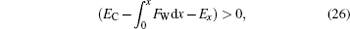 |
where EC represents the IFE of the Cassie droplet, which can be found when x in Eq. (13) is zero,
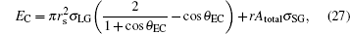 |
in which θ EC is the equilibrium contact angle of the Cassie drop
 |
The calculation diagram and the corresponding calculating program of the droplet C– W transition are shown in the supplementary information.
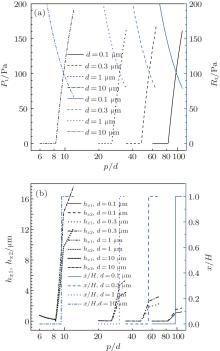
Figure 3 shows the C– W transition pressure Pt, the C– W transition resistance Rt, and the parameters of the curved liquid– air interface of a 2 μ L sessile droplet on textured surfaces with different structural parameters. Firstly, it can be seen from Fig. 3(a) that Pt is always 0 while Rt is very large if p/d of posts with a certain diameter is relatively small. Only when p/d is greater than a critical value, Pt starts to increase rapidly while Rt decreases sharply with the increase of p/d. Meanwhile, the smaller the micro/nano pillar diameter, the larger the critical value of p/d, and the greater the Rt, which means that large pitch is needed for small diameter posts to make Pt acting on the droplet exceed Rt so that the droplet can complete the C– W transition. Consequently, the thinner the pillars, the more favorable the prevention of the C– W transition. Namely, nano rough structures are able to maintain droplets in the superhydrophobic state more effectively. The fundamental of this result is explained as follows. The r will increase as d declines according to Eq. (14) if p/d keeps unchanging. Then Rt will increase while Pt decreases under this condition.
The effect of the textured parameters on the C– W transition can be more clearly seen by comparing Fig. 3(a) with Fig. 3(b). When Pt acting on the droplet is larger than 0 (Fig. 3(a)), the two bending depths, hx1 and hx2, of the meniscus begin to correspondingly increase quickly (Fig. 3(b)). Moreover, when Pt ≥ Rt (Fig. 3(a)), the TPCL beneath the droplet starts to move downward suddenly, that is x/H in Fig. 3(b) changing abruptly from 0 to 1. This fully shows that the liquid– air interface below the droplet becomes curved gradually and then obviously when Pt is greater than 0, and the TPCL begins to shift when Pt ≥ Rt. Besides, it can also be found from Fig. 3(b) that the larger the diameter of the posts, the more obvious the curvature of the meniscus, which is caused by the fact that the distance between the pillar side walls, p − d, is substantial when the diameter is large even if p/d is not great. For instance, if the diameter of one type of posts is 1 μ m and p/d is 30, the p − d will be 29 μ m; while the p − d will become 80 μ m if the diameter of another type of pillars is 10 μ m, even the p/d is 9 in this case.
The droplet size affects the wetting state evidently. Generally, the smaller the droplet, the easier its C– W transition when it sits on a surface with fixed structural parameters. The calculation results of the model for this phenomenon are shown in Fig. 4. It is clear that Rt acting on the droplet has no relation with its volume, but is relevant to the structural parameters and the physicochemical properties of the material. However, Pt acting on the droplet has an obvious relation with its volume. There exists a critical volume for the droplet on a textured surface. When the volume of the droplet is less than the critical value, Pt increases obviously, but when it is larger than the critical value, Pt is 0, which means that a small droplet will suffer great Pt so that it is easy to transit to the Wenzel state while a large droplet may not be acted by Pt so that it will remain in the Cassie state. At the same time, the critical volume is clearly relative to the structural parameters. The smaller the pillar diameter, the smaller the critical volume, which also indicates that nano-structure is able to prevent droplets from the C– W transition. For instance, when the pillar diameter is 0.1 μ m, a droplet as small as a nano litre could keep the Cassie state, but when the pillar diameter becomes 1 μ m, a droplet of 0.1 mL will be in the Wenzel state.
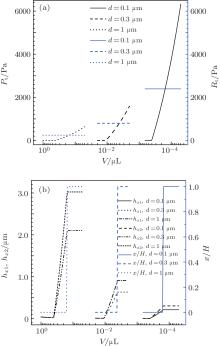 | Fig. 4. Effects of drop volume on (a) C– W transition pressure and resistance and (b) liquid– air interface parameters below droplets. Here θ I = 110° , θ A = 115° , p/d = 20, and H = 10 μ m. |
The above results indicate that the essential reason for the droplet spontaneous transforming from Cassie to Wenzel state while its size reduces is that the transition pressure Pt will increase constantly with its size decreasing whereas the transition resistance Rt remains unchanging. When the driving force is greater than the resistance, the spontaneous C– W transition will be completed.
The wetting state of a droplet obviously depends on its volume and the superhydrophobicity of a tiny droplet is usually expected to be sustained, it is important to study the critical volume of droplets transiting from Cassie to Wenzel state on different structural surfaces. The calculation result is shown in Fig. 5. First of all is the effect of the pillar height H. When H is 1 μ m or lower, even a little bending of the liquid– air interface beneath the droplet will lead to the C– W transition through the sag mechanism. Consequently, it is almost impossible even for a large droplet, such as 10 μ L in this calculation, to maintain the Cassie state when H is low enough. When H is high enough, however, the critical volume decreases obviously. In this condition, the C– W transition takes place definitely through the TPCL depinning impalement. The second is the effect of p/d, which is similar to the result above. The smaller the value of p/d, the more difficult the C– W transition, and thus the smaller the critical volume. Besides, the effect of the pillar diameter can be found if comparing Fig. 5(a) with Fig. 5(b). Namely, the smaller the pillar diameter, the more difficult the C– W transition, and the smaller the critical volume. For instance, when d = 1 μ m, the critical volume is samller than one nano litre. Therefore, nano architectures can avoid the C– W transition of tiny droplets effectively.
The above mainly investigates the effects of the structural parameters and the droplet volume on the C– W transition. There are two other parameters, the intrinsic contact angle and the advancing contact angle, which also influence the transition, as shown in Fig. 6. It is clear that the C– W transition pressure Pt decreases obviously while the transition resistance Rt rises with the increase of the intrinsic contact angle (Fig. 6(a)). As a result, the critical volume declines (Fig. 6(b)). Additionally, the increase of the advancing contact angle can also make Rt enlarge and Pt reduce in a certain extent (Fig. 6(a)). The critical volume is also decreased in this case, but not as obviously as that influenced by the intrinsic contact angle (Fig. 6(b)).
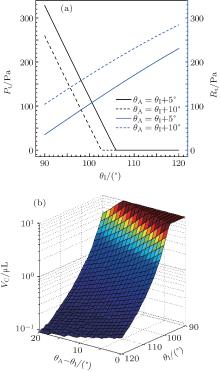 | Fig. 6. Effects of intrinsic contact angle and advancing angle on (a) C– W transition pressure and resistance and (b) critical volume VC. Here p = 75 μ m, d = 10 μ m, H = 20 μ m, and V = 2 μ L. |
Although increasing the intrinsic contact angle can effectively hinder the C– W transition, the intrinsic contact angle of current hydrophobic materials is generally under 120° . Consequently, it seems difficult to further restrain the C– W transition only relying on the change of the chemical properties of the materials. On the other hand, nano structures or micro-nano hierarchical textures have been proved to be able to effectively suppress the C– W transition.[16, 39, 40] Thereby, the superhydrophobicity of droplets on these surfaces can be maintained. Furthermore, the sag mechanism may be no longer valid for the droplet C– W transition on a two-tier surface, i.e., a composite droplet will not transform to a Wenzel one even though its meniscus touches the micro structural substrate, [41– 43] the fundamental of which needs to study further.
There are two types of experiments to study the droplet C– W transition on superhydrophobic surfaces. One is to observe the contact angles of the droplets with fixed volume sitting on textured surfaces with different structural parameters. And the sudden change of the contact angles reflects the C– W transition. The other is to detect the abrupt variation of the shape parameters of the droplet before and after the C– W transition during its evaporation on a textured surface. The measurement results with these two types of experiments and the corresponding calculation outcomes with the model are shown in Figs. 7– 9.
 | Fig. 7. Changes of contact angle and IFE barrier Eb of sessile droplets before and after C– W transition on different textured surfaces. (a) Experimental data originate from literature, [13]H = 10 μ m when d = 5 μ m, H = 30 μ m when d = 14 μ m; V = 5 μ L, θ I = 109° , θ A = 109° . (b)– (d) Experimental data originate from literature, [22]V = 3 μ L, θ I = 110° , θ A = 116° , (b) d = 10 μ m, H = 40 μ m; (c) p = 50 μ m, H = 20 μ m; (d) H = 2 × d. (e) Experimental data originate from literature, [21]d = 105 μ m, H = 150 μ m, V = 4.3 μ L, θ I = 107.5° , and θ A = 107.5° . Here the IFE barrier of the C– W transition is defined as the difference between the IFE of a composite droplet when its bottom TPCL moves to x = H and the IFE of Cassie state droplet. |
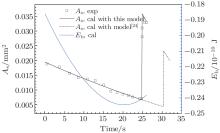 | Fig. 8. Changes of base area As and IFE barrier Eb of a droplet before and after its C– W transition during evaporation. Experimental data originate from literature.[11] Here d = 3 μ m, p = 20 μ m, H = 4.8 μ m, θ I = 110° , θ A = 116° . Note: 1) the droplet volume required in the model calculation is solved by using the measured droplet base area and receding contact angle; 2) the IFE barrier of the C– W transition is defined as the difference between the IFE of a composite droplet when its bottom TPCL moves to x = H and the IFE of the Cassie state droplet. |
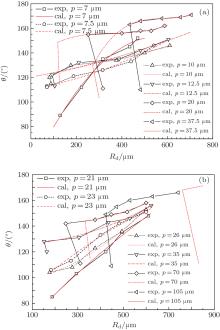 | Fig. 9. Changes of contact angle and drop radius Rd before and after the C– W transition of droplets during evaporation. Experimental data originate from literature, [13]θ I = 109° , θ A = 109° ; (a) d = 5 μ m, H = 10 μ m; (b) d = 14 μ m, H = 30 μ m. Here the droplet volume required in the model calculation is solved by using the measured droplet radius and the contact angle. |
As shown in Fig. 7, the contact angles of the sessile droplets on different textured surfaces all decrease abruptly after they transit from Cassie to Wenzel state. The model calculation results are generally in good agreement with the measured ones.[13, 21, 22] It can be seen from Figs. 7(a), 7(b), 7(d), and 7(e) that the increase of the pillar pitch eventually results in the droplet C– W transition. And from Fig. 7(c), it can be found that the droplets become easily appearing in the Cassie state with the increase of the pillar diameter while Wenzel droplets emerge on the surfaces with small diameters of posts.
It is generally considered that the C– W transition is restricted by the IFE energy barrier.[22, 26, 40, 44– 46] Once this energy barrier decreases to 0, the C– W transition should be accomplished.[11] However, the comparison between the calculation of this study and the measured results on different textured surfaces indicates that the droplet C– W transition usually does not happen when the energy barrier is zero, but often takes place when the energy barrier is obviously smaller than zero[22] (Figs. 7(a)– 7(c)). The main reason for this is that the energy barrier is only a state function, which depends on the difference of the droplet IFE in two states.[22] However, the C– W transition is also related to the process route, i.e., associated with the process of the TPCL moving along the structural side walls.[46] Therefore, it is necessary to consider not only the energy barrier but also the process resistance, then the C– W transition can be accurately determined.
The Laplace pressure inside a droplet was considered as the driving force of the C– W transition in several reports.[1, 5, 15] By the balance of capillary and Laplace pressure, a formula of drop radius at the moment of transition was found.[25] Here the contact angles before and after drop the C– W transition in Fig. 7 are also calculated with this formula and compared with the experiments and our theoretical results. It can be seen that in most cases, the transition points calculated by the Laplace pressure method usually appear earlier or easier for the sessile drops on these surfaces as compared with the experiments.
When a Cassie state droplet evaporates on a structural surface, the C– W transition pressure acting on the droplet becomes larger as the drop size reduces. Consequently, the droplet will spontaneously transit into the Wenzel state at a certain moment. It can be seen from Fig. 8 that the base area of the droplet abruptly increases obviously when the C– W transition takes place. The C– W transition point calculated by this model fits the measured value[11] very well. Meanwhile it is visible that the IFE energy barrier of the droplet is always negative during the evaporation process. Thus the droplet C– W transition during evaporation cannot be determined with the energy barrier being 0. Furthermore, the C– W transition point determined by the balance of capillary and Laplace pressure[25] is obviously delayed.
As shown in Fig. 9, the size of an evaporating droplet when its C– W transition is taking place is obviously relative to the pillar pitch p. When p is small, there is no C– W transition happening for all the droplet sizes during evaporation since the contact angles do not decrease obviously. However, if p is large enough, the C– W transition occurs when the droplet size reduces to a critical value, at which the contact angle of the droplet decreases suddenly and the radius of the droplet increases obviously. Overall, the calculation results of the model agree well with the measured values[13] except for the detailed transition points where there are deviations between the calculations and the measurements. For instance, the calculated critical radius of the droplet C– W transition is less than the measured value for the case of d = 5 μ m (Fig. 9(a)), while it becomes larger than the value for the case of d = 14 μ m (Fig. 9(b)). Considering the complexity of the dynamic process of droplet evaporation, the deviation between calculation and measurement of the C– W transition point is acceptable.
The model can be reliable to analyze the mechanism of the droplet C– W transition since the calculation results on the whole fit experiments well.
From the movement of small molecules to the sliding of large objectives on inclined hills, all follow the basic law that an object spontaneously migrates from a high-energy position to a low-energy one. The energy gradient of the object, i.e., the difference between the high and low energies at two positions divided by the distance, is the driving force for the objective to move. This basic law is applied to the spontaneous C– W transition of droplets in this study. And the IFEG as the C– W transition driving force of droplets is proposed and derived (Eq. (16)) for the first time, and the droplet C– W transition pressure is defined (Eq. (19)). Thus the origin and nature of the spontaneous C– W transition driving force and the collapse mechanism of droplets can be well explained. The C– W transition pressure proposed here is neither gravity nor hydraulic pressure, but originates from the IFEG, which is clearly associated with the droplet size and the structural parameters and increases obviously with the decrease of the droplet size. As a result, the phenomenon that the spontaneous C– W transition of an evaporating droplet takes place only after its size reduces to a critical value can be reasonably explained. However, with either gravity or hydraulic pressure, this phenomenon cannot be interpreted.
On a solid surface with surface energy gradient, a droplet could move from low surface energy position to high energy one.[47– 52] It is generally considered that the nature of this gradient is a kind of wetting gradient.[1, 4, 6] Namely, a droplet always tends to go to the more wetting position. In fact, this gradient is different from the IFEG owned by a droplet proposed in this study since the former is only the result of the surface energy change on a solid surface. Only the latter is able to reflect the law that an object moves always from the high energy place to the low energy one, while the former cannot. In fact, the problem of droplets climbing upwards on an inclined surface with surface energy gradient could also be explained and calculated well with the IFEG proposed here. That is, the height of a droplet climbing up can be solved through the calculation of the droplet IFEG at a certain position, and by comparison of the IFEG with the TPCL moving resistance. Such calculation has not been reported in the published literatures.[47– 52]
It is generally considered and confirmed by experiments that the droplet C– W transition will be completed once the meniscus below the droplet touches the structural substrate, i.e., via the sag mechanism.[12] The sag impalement is right for single micro rough surfaces with intrinsic contact angle less than 120° . However, the study of Luo et al.[41] indicated that the C– W transition could not be accomplished via the sag mechanism if the intrinsic contact angle is as large as 135° . Namely, a droplet cannot transit to the Wenzel state although its meniscus touches the structural substrate in this case. Indeed the intrinsic contact angle of current materials is hardly greater than 120° , so the above circumstance rarely happens. However, the apparent contact angle of a micro structural surface can be enormously enlarged if nano architectures are prepared on the micro textures. The experimental results[41– 43] really showed that the sag mechanism is indeed not valid on the micro/nano two-tier surfaces. In this case, even if the meniscus beneath the droplet contacts the micro structural substrate, the sagging triggered C– W transition could not be completed because the nano architecture exists on the micro texture and the corresponding apparent contact angle is very large, so that the wetting force to overcome during the sag process is large.
Therefore, this model cannot be used for the C– W transition when the sag mechanism is not valid. That is, the model is not valid when the intrinsic contact angle of the textured surfaces is much larger than 120° or when a superhydrophobic surface has a suitable micro-nano hierarchical structure. The detailed sag process after the front of the liquid– air interface beneath the droplet touches the structural substrate will be studied further.
Since drop sizes considered in this model are all samller than the capillary scale, the influence of gravity can be ignored.[12] For droplets with large sizes, the gravity can be added directly into Eqs. (6) and (16). Namely, the C– W transition driving force of a large droplet on a horizontal textured surface includes IFEG and gravity. Then the shape of the large droplet is no longer a segment but similar to an elliptic segment. Equations (13) and (27) cannot be applied to calculate its IFE but need to be modified.
All above results are obtained for water under normal temperature and pressure if there is no special clarification. The influence of temperature and pressure on the droplet C– W transition can be attributed to their effects on the surface tension, density, and intrinsic contact angle in this model.
Additionally, the above droplet C– W transition was modelled only under static air condition without gas flow. For the complicated case with air flow, the shear stress on the droplets should be included in the model so that the comprehensive effects of multi-parameters on the droplet C– W transition can be calculated.
Finally, this theoretical model may be applied to other liquids if their intrinsic contact angles are greater than 90° . But for organics or oil droplets with intrinsic contact angles smaller than 90° , the model is no longer valid since the model calculation will show that there is no repellence for these droplets on rough surfaces and Cassie drops will always transit to the Wenzel state unconditionally in this case. In fact, it is the complicated structures which prevent the Cassie droplets to collapse in this situation and our model is limited to calculate the effect of these complex textures.
When a sessile droplet smaller than the capillary length on a superhydrophobic surface is acted by the C– W transition pressure resulted from its IFEG, the liquid– air interface beneath the droplet begins to bend. The smaller the droplet, the larger the transition pressure, the greater the curvature of the meniscus below the droplet. The meniscus touches the structural substrate either directly or after the depinning of TPCL to complete the C– W transition. Micro/nano structural parameters obviously influence the C– W transition pressure and the curved extent of the meniscus. The transition is difficult to take place for droplets sitting on thin posts, such as nano asperities, whereas the meniscus beneath the droplet is easily to contact the structural substrate when the pitch of the pillars is too large or the height of the asperities is too low. Nano textured surfaces with suitable pillar pitch and height and/or micro-nano hierarchical surfaces are able to effectively prevent the droplet C– W transition.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|