Cite this Article
Li Hui-Dong, Wang Zhan-Hui, Weiland Jan, Feng Hao, Sun Wei-Guo. Simulations of the L–H transition dynamics with different heat and particle sources* . Chinese Physics B, 24(11): 115204  
Permissions
Simulations of the L–H transition dynamics with different heat and particle sources*
Li Hui-Donga), Wang Zhan-Huib), Weiland Janc), Feng Haoa), Sun Wei-Guoa),d)
School of Science, Research Center for Advanced Computation, Xihua University, Chengdu 610039, China
Southwestern Institute of Physics, Chengdu 610041, China
Department Applied Physics, Chalmers. University of Technology and Euratom-VR Association, S41296 Gothenburg, Sweden
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China

†Corresponding author. E-mail: zhwang@swip.ac.cn

Corresponding author. E-mail: fenghao@mail.xhu.edu.cn

*Project supported by the Funds of the Youth Innovation Team of Science and Technology in Sichuan Province, China (Grant No. 2014TD0023), the National Natural Science Foundation of China (Grant Nos. 11447228 and 11205053), and the China National Magnetic Confinement Fusion Science Program (Grant No. 2013GB107001).

Abstract

It is crucial to increase the total stored energy by realizing the transition from a low confinement (L-mode) state to a high confinement (H-mode) state in magnetic confinement fusion. The L–H transition process is simulated by using the predictive transport code based on Weiland’s fluid model. Based on the equilibrium parameters obtained from equilibrium fitting (EFIT) in the experiment, the electron density ne, electron temperature Te, ion temperatures Ti, ion poloidal Vp, and toroidal momenta Vt are simulated self-consistently. The L–H transition dynamic behaviors with the formation of the transport barriers of ion and electron temperatures, the electron density, and the ion toroidal momenta are analyzed. During the L–H transition, the strong poloidal flow shear in the edge transport barrier region is observed. The crashes of the electron and ion temperature pedestals are also observed during the L–H transition. The effects of the heating and particle sources on the L–H transition process are studied systematically, and the critical power threshold of the L–H transition is also found.

Keyword: 52.35.Py; 52.70.La; 52.55.Tn; 52.55.Fa; magnetic fusion; tokamak plasma; L–H transition; transport barriers
1. Introduction

It is crucial to increase the total stored energy by realizing the transition from a low confinement (L-mode) state to a high confinement (H-mode) state in magnetic confinement fusion. The H-mode is usually characterized by an edge pedestal, in which the plasma will achieve a longer global energy confinement time and a higher plasma pressure.[1] It is critical for ignition and burning plasma operation, which is viewed as a key operation mode for future burning plasma experiments and the ultimate fusion reactors. The magnetic confinement plasma will make a spontaneous transition from a low confinement (L-mode) state to a high confinement (H-mode) state when the input heating power is strong enough and exceeds the critical heating power threshold.[2] The underlying physics behind the L– H transition has not been explained well to date. The H-mode operation can be controlled successfully and easily only when the physics of the L– H transition is really understood. Extensive research efforts have been made to control the L– H transition.[3] The L– H transition is characterized by a rapid suppression of the edge turbulence, a reduction of the Dα light emission intensity, the formation of a sharp edge pressure pedestal and a radial electronic well, an increase of the E × B shearing rate, and the formation of particle and energy transport barriers.[4] The L– H transition has been studied experimentally and theoretically.[4– 8] The importance of the E × B flow shear for the L– H transition has been recognized.[5] One of the most convincing explanations for the L– H transition is the suppression of turbulence by the E × B flow shearing effects, [5] which have been proved by many experiments in the tokamaks.

Most of the experiments have reached the conclusion that the realization of the L– H transition requires sufficient plasma heating and fueling sources to exceed the power threshold, meanwhile it can trigger the formation of an edge transport barrier.[6] The underlying physics and especially the dynamics near the power threshold of the L– H transition have not been revealed, although some theoretical models have been proposed[3, 6, 7, 9– 12] and the theoretical studies of the L– H transition have been reviewed in Ref. [13]. Thus, the research on the L– H transition is still the present hottest topic of tokamak plasma. To obtain a long pulse H-mode discharge, there are still lots of experiments and simulations focusing on the key factors of the L– H transition and the evolution principles of the relevant physical quantities.[10, 14– 29] Among the theoretical models proposed for the L– H transition, the fluid model proposed by Weiland[30] is one of the well-known models to reveal the L– H transition process, which has been utilized to simulate and realize the L– H transition in EAST tokamak.[31] The Weiland model is the main part of the MMM, [32] it has been benchmarked and validated in many studies, [33– 35] and it has also been used by some theoretical researchers, [36, 37] to study the particle transport.

In the present work, the model is used for simulating the L– H transition dynamics in tokamak plasma. The theoretical model is described in Section 2. The simulation results are presented in Section 3. Finally, the principal results are summarized in Section 4.

2. Theoretical model

The Weiland’ s fluid model[30, 31] is used in the simulations. This model is capable of presenting the turbulent transport flux, the self-consistent radial force balance equation provides an E × B flow shear depending on the mean profiles, and finally the E × B flow shear gives feedback to the transport.

The edge boundaries of the density and the temperature are fixed at the values taken from the experiment. Sometimes they will be modified within the experimental error bars. The inner boundaries are flat. For the poloidal rotation, the boundary condition is taken as the initial edge neoclassical vnc. For the toroidal rotation, the boundary condition is set to be − 100 vnct, where vnct is the projection of the neoclassical rotation in the toroidal direction.

In the model, the transport dynamic information is mainly contained in the particle flux Γ Pα , the momentum flux Φ iα , and the energy flux Qα . They are usually parameterized by analogy to Fick’ s law as follows:

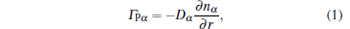The foundational equations of the Weiland model are the reactive reduced Braginskii multi-fluid equations. The fluid resonance effect is also included in the energy equation as shown below

where

Here, the convective diamagnetic part of ∇ · q cancels other convective diamagnetic parts in the energy equation, thus there is only the curvature part left which gives rise to the perpendicular fluid resonance.

The saturation level of the electric potential without flow shear is

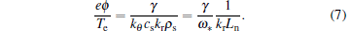By using the Waltz rule[38, 39] and replacing the flow shear rate with

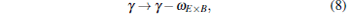we have

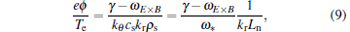where kr ≈ 1/Lr and Lr is the radial correlation length. Then the transport will change from the simplest electrostatic ITG mode into the following form:[30]

From Eq. (10), we can see how the total saturation level influences the thermal diffusivity due to the combined influence of the E × B convection and the Waltz rule. The Waltz rule is always used for the transport, when the γ − ω E× B < 0 holds, the mode will be turned off.

The flow shear rate can be written as

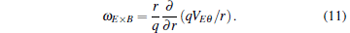In order to calculate the flow shear rate as VEθ = Er/B, we need to know the radial electric field obtained from the radial force balance

The toroidal flow will be simulated by the parallel momentum transport equation

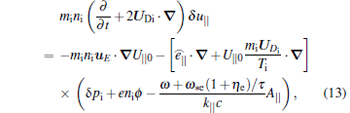or

where

The toroidal rotation averaging over time and spatial scales of the fluctuations is calculated as follows:

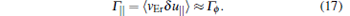The toroidal momentum transport is calculated in the usual way as

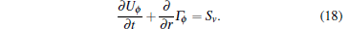The poloidal flux is given by the Reynolds stress as

Then

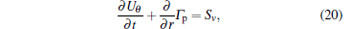where

Here the neoclassical rotation vnc is used.[40]

In the Weiland’ s fluid model, many different instabilities, such as the slab and toroidal ITG, trapped electron modes driven by charge separation, compression, or collisions, resistive ballooning modes, [30, 41] MHD and kinetic ballooning modes, and peeling modes, are included. The relation between the drift type and the MHD type modes is explained by the parallel electric field which is obtained from the relation between the electrostatic and magnetic potentials. The MHD type modes, particularly the kinetic ballooning modes and peeling modes, are important in the H-mode plasma. The MHD type modes and drift type modes are included all the time. The physics conditions will determine which modes are the most important, while they will coexist.

To obtain this, the following free electron continuity and parallel momentum equations are used:

Combining the above two equations, we can obtain

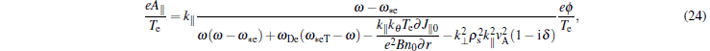where

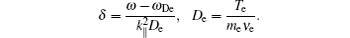
Quasi-neutrality will force the ion particle transport to be equal to electron particle transport (impurities are taken as a fixed fraction of the electron density). More details of this equation were given in Refs. [30] and [31].

3. Simulation results
3.1. Process of the L– H transition

The machine parameters used in the present simulation are as follows: the aspect ratio ɛ = 0.24, the elongation κ = 1.05, the minor radius r0 = 0.4 m, and the major radius R0 = 1.65 m. The equilibrium magnetic field B0 = 1.34 T. The time step 10− 5 s is used in the simulation. For obtaining a better resolution of the edge transport barriers, the normalized radial resolution domain is selected to be in a range from 0.63 to 1.0. The total input heating power Pi is about 0.6 MW. The deposition profile of the heating power and the profile of the edge particle source are shown in Fig. 1.

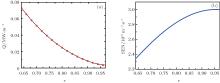Fig. 1. (a) Deposition profile of the heating power and (b) profile of the edge particle source used in the simulation.

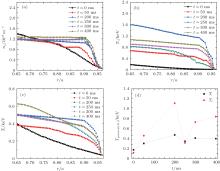
In order to study the L– H transition in detail, it is simulated for a long enough time to cover the whole period of the L– H transition, ∼ 600 ms, with the heating power P = 1.0Pi and the edge source strength SEN = 1.0 × 1019 m3· s− 1. The plasma profiles at different times are plotted in Fig. 2. It can be seen that the height of the density barrier increases gradually with time going by. The heights of both electron and ion temperature barriers increase before t = 200 ms, but a sudden drop appears at t = 250 ms. The barrier heights of both the electron temperature and the ion temperature will go up again later, but they will not reach values as high as those at t = 200 ms. This process is clearly shown by the variations of ion and electron temperatures on the top of the pedestals (Fig. 2(d)). It seems that the barrier will crash and oscillate as time goes by, especially for the temperature profiles. The crash appears to be edge localized modes (ELMs), i.e., the gradient increases with time going by until it passes the MHD limits. Then the transport increases strongly and the gradients decrease back to the L-mode. The plasma is below the critical gradient and it will go back to the H-mode again with continuous heat and particle source.

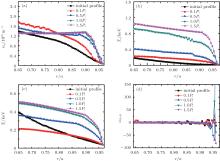
Fig. 2. Time evolutions of (a) electron density ne, (b) electron temperature Te, (c) ion temperature Ti profiles with the initial heating power Pi and the edge source SEN = 1.0 × 1019 m− 3· s− 1. (d) Variations of ion and electron temperatures on the top of the pedestals. The L– H transition process is observed, and the transport barriers are formed during the simulation.

Figure 2 shows the time evolutions of the mean plasma profiles. It is obvious that the L– H transitions occur and the pedestal heights increase gradually with continuously heating and fueling. To study the physics characters of the L– H transition in more detail, the simulation profiles at t = 140 ms are given in Fig. 3. The curves with squares are the initial profiles for each quantity, and the curves with circles are those simulated by Weiland’ s fluid model. The simulated profiles of electron density ne, electron temperature Te, ion temperature Ti, poloidal momentum Vp, and flow shear rate ω E× B all suggest that the edge transport barriers are formed, which indicates that the plasma is in the H-mode at the moment. The profiles of poloidal momentum Vp and flow shear ω E× B display strong edge shears, which reduce the turbulence intensity and play a key role in the L– H transition in tokamak plasma.[2, 4, 5] The toroidal momentum Vt profile forms a pedestal far from the edge of the plasma. The toroidal rotation is important for triggering the barrier since it can reduce or enhance the radial electric field due to the poloidal rotation. In the simulations, the initial profile of the poloidal rotation is entirely neoclassical while the toroidal rotation has a boundary (fixed) due to the intrinsic rotation.

Fig. 3. Profiles of (a) electron density ne, (b) electron temperature Te, (c) ion temperature Ti, (d) poloidal velocity Vp, (e) toroidal velocity Vt (for velocity V, positive refers to the clockwise direction and negative the anticlockwise direction), and (f) the E × B flow shear rate ω E × B profiles (lines with circles) at t = 140 ms and the initial profiles at t = 0 ms (lines with squares). Transport barriers of the electron density, electron temperature, and the ion temperature produced. The flow shear near the boundary is observed.

3.2. Effects of heat and particle sources on the L– H transition

In order to study the effects of the heat and particle sources on the L– H transition, the profiles of electron density, electron temperature, and ion temperature varying at different time are simulated in the absence of the heat and particle sources. The initial ion temperature is higher than the electron temperature. The ion temperature decreases as time increases, while the electron temperature increases in the early time due to the energy interchange between electrons and ions. When the ions and the electrons are thermally balanced, the temperatures of both species will reduce simultaneously due to the radiation effect. The energy will transfer much faster from the hotter ions to the electrons in the core plasma due to collisions, thus the inner temperature decreases rapidly and the inner electron temperature increases much faster than the edge electron temperature, forming a pedestal-like structure. In the absence of the particle source, the density profile is almost stable (Fig. 4).

Fig. 4. Profiles of (a) density ne, (b) electron temperature Te, and (c) ion temperature Ti simulated in the absence of heat and particle sources.

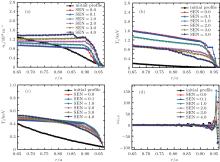
3.2.1. The effect of heat source on the L– H transition

In order to display the process of the barrier formation in more detail, the profiles of electron density, electron temperature, and ion temperature at different times are given with the increased heating power 1.5Pi in Fig. 5. Similar results to those predicted at a heating power of 1.0Pi are obtained. The density pedestal is set up gradually. It is about 50 ms from the initial simulation, the pedestals of electron density ne and temperature Te become obvious, and the heights of the barriers increase slowly with time. Interestingly, the height of the electron temperature does not increase monotonically. It reaches a maximum at about t = 80 ms, comes down at about t = 120 ms, then goes back to a relatively large value at about t = 140 ms. It means for the crash of the electron barrier, however, no similar phenomena for the profiles of electron density and ion temperature are observed.

Fig. 5. Simulated profiles of (a) electron density ne, (b) electron temperature Te, and (c) ion temperature Ti at different time with the heat power P = 1.5 Pi and the edge source SEN = 3.0 × 1019 m− 3· s− 1.

The profiles of electron density ne, electron temperature Te, and ion temperature Ti at t = 140 ms with different heating powers are displayed in Fig. 6. As shown in the figure, the edge transport barriers of both density and temperature are not formed once the heating power is 0.1Pi. With the increase of the heating power, the transport barriers are formed and become more and more apparent. The results indicate that the density barriers are formed more easily than the temperature barriers. The profiles also indicate that the density barrier and the ion temperature barrier will saturate when the heating power increases up to 1.5Pi, while the electron temperature barrier still increases. The power threshold is about 0.5Pi, ∼ 0.3 MW, in our simulations. When the heating power is 0.5Pi, the flow shear rate is even stronger than that simulated using the much higher heating powers 1.0Pi, and 1.5Pi. The underlying physics behind the L– H transition near the power threshold and the dependence of the power threshold on tokamak plasma conditions are complicated, which will be revealed in the further studies later.

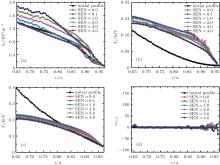
Fig. 6. Profiles of (a) simulated electron density ne, (b) electron temperature Te, (c) ion temperature Ti, and (d) flow shear rate ω E × B at t = 140 ms with different heat powers and fixed edge source SEN = 3.0 × 1019 m− 3· s− 1.

3.2.2. Effects of particle source on the L– H transition

In simulations of the transport barrier formation, a source is located near the plasma edge boundary. To study the influence of the edge source on the simulated profiles, several different sources are compared for two different heat power sources, 1.0Pi and 0.1Pi, respectively (Figs. 7 and 8). Comparing the two sets (1.0Pi and 0.1Pi) of the simulated profiles, we can see that only enough heating power is necessary to form the transport barriers, which implies the existence of the power threshold. At low heating power, it is difficult to form a transport barrier even though there is a large enough particle source near the edge. The flow shear rate with low heating power is also much lower (Fig. 8) than that simulated with strong heating power (Fig. 7). When the heating power is strong enough, the height of the density barrier rises with the increase of the strength of the particle source. However, the temperature barrier will be restricted by the relatively strong edge particle source as the height of the temperature barrier decreases with the increase of the particle source as shown in Fig. 7. In this case, the flow shear rate ω E× B exhibits a similar trend to that of the temperature barrier, namely, a strong edge particle source will restrict the flow shear rate. Physically, when there is a strong particle source, the heating power will be diluted by more particles, then the temperatures will be reduced. It is natural that a strong particle source will produce a higher density transport barrier and lower temperature transport barriers.

Fig. 7. Profiles of (a) density ne, (b) electron temperature Te, (c) ion temperature Te, and (d) flow shear rate ω E× B at t = 140 ms with different edge particle sources when the heating power P = 1.0Pi.

Fig. 8. Profiles of (a) density ne, (b) electron temperature Te, (c) ion temperature Te, and (d) flow shear rate ω E× B at time t = 140 ms with different edge particle sources when the heating power P = 0.1Pi.

4. Summary and discussion

The H-mode has been realized and the transport barriers are formed in the present L– H transition simulations based on the Weiland’ s fluid model. The effects of the heat and the particle sources on the L– H transition have been studied in the present paper. The results show that a strong enough heating power above the threshold is necessary to realize an L– H transition. With strong heating power, the height of the density pedestal increases nearly monotonically with the strength of the edge particle source increasing, however, the temperature pedestals do not perform similarly to that of the density pedestal, and it will be constrained by the stronger particle source. At low heating power, even though the particle source is strong enough, it is difficult to form the edge transport barrier.

The principal results in the present study are summarized as follows.

(i) The transition from the L mode to the H mode is realized by using the Weiland’ s fluid model. Apparent transport barriers for the density, electron temperature, ion temperature, and toroidal velocity are simulated and formed near the edge of the tokamak plasma.

(ii) The power threshold is found to be in a range of about 0.5Pi, ∼ 0.3 MW, for the occurrence of the L– H transition through the present simulation, and this power threshold will be influenced by the strength of the edge particle source. At a strong heating power, the height of the density barrier rises with the increase of the strength of the particle source. The temperature barrier will be restricted by the strong edge particle source, and the height of the temperature barrier will decrease when the particle source increases.

(iii) The heights of the transport barriers of the electron temperature and the ion temperature seem to crash with the increase of time, especially for the electron temperature, and this kind of crash appears to be related to the occurrence of the ELMs.

(iv) The dynamic characteristics during the L– H transition are studied: the strong poloidal velocity and flow shear are predicted near the edge of the plasma.

In the following study, the evolution of MHD instabilities during the L– H transition will be investigated. Also, some transport characteristics of the tokamak plasma, such as the transport coefficients, the magnetic shear, and the flow shear, near the threshold power can be further studied. The underlying physics of the L– H transition near the power threshold and the dependence of the power threshold on the tokamak plasma conditions will be studied later. Some other physical process, including the I-phase process and the L– I– H or H– I– L transition, can also be studied in the coming research.

Acknowledgement

The authors wish to thank Wang A K, Wang G Q, Ma J, Xu M, Wang Z T, Zhong W L, and Xia F for their fruitful discussion.

Reference
1 Wagner F, Fussmann G, Grave T, Keilhacker M, Kornherr M, Lackner K, McCormick K, Muller E R, Stabler A, Becker G, Bernhardi K, Ditte U, Eberhagen A, Gehre O, Gernhardt J, Gierke G V, Glock E, Gruber O, Haas G, Hesse M, Janeschitz G, Karger F, Kissel S, K1über O, Lisitano G, Mayer H M, Meisel D, Mertens V, Murrnann M, Poschenrieder W, Rapp H, Rohr H, Ryter F, Schneider F, Siller G, Smeulders P, Soldner F, Speth E, Steuer K H, Szymanski Z and Vollmer O 1984 Phys. Rev. Lett. 53 1453 DOI:10.1103/PhysRevLett.53.1453 [Cited within:1]
2 Keilhacker M 1987 Plasma Phys. Control. Fusion 29 1401 DOI:10.1088/0741-3335/29/10A/320 [Cited within:2]
3 Miki K, Diamond P H, Fedorczak N, Gürcan Ö D, Malkov M, Lee C, Kosuga Y, Tynan G, Xu G S, Estrada T, McDonald D, Schmitz L and Zhao K J 2013 Nucl. Fusion 53 073044 DOI:10.1088/0029-5515/53/7/073044 [Cited within:2]
4 Yan Z, McKee G R, Fonck R, Gohil P, Groebner R J and Osborne T H 2014 Phys. Rev. Lett. 112 125002 DOI:10.1103/PhysRevLett.112.125002 [Cited within:3]
5 Burrell K H 1997 Phys. Plasmas 4 1499 DOI:10.1063/1.872367 [Cited within:3]
6 Miki K, Diamond P H, Hahn S H, Xiao W W, Gürcan Ö D and Tynan G R 2013 Phys. Rev. Lett. 110 195002 DOI:10.1103/PhysRevLett.110.195002 [Cited within:2]
7 Kim E and Diamond P H 2003 Phys. Rev. Lett. 90 185006 DOI:10.1103/PhysRevLett.90.185006 [Cited within:1]
8 Estrada T, Hidalgo C, Happel T and Diamond P H 2011 Phys. Rev. Lett. 107 245004 DOI:10.1103/PhysRevLett.107.245004 [Cited within:1]
9 Fundamenski W, Militello F, Moulton D and McDonald D C 2012 Nucl. Fusion 52 062003 DOI:10.1088/0029-5515/52/6/062003 [Cited within:1]
10 Xu G S, Shao L M, Liu S C, Wang H Q, Wan B N, Guo H Y, Diamond P H, Tynan G R, Xu M, Zweben S J, Naulin V, Nielsen A H, Rasmussen J J, Fedorczak N, Manz P, Miki K, Yan N, Chen R, Cao B, Chen L, Wang L, Zhang W and Gong X Z 2014 Nucl. Fusion 54 013007 DOI:10.1088/0029-5515/54/1/013007 [Cited within:1]
11 Weymiens W, Blank H J and Hogeweij G M D 2013 Phys. Plasmas 20 082306 DOI:10.1063/1.4817945 [Cited within:1]
12 Dam M, Brøns M and Rasmussen J J 2013 Phys. Plasmas 20 102302 DOI:10.1063/1.4823719 [Cited within:1]
13 Connor J W and Wilson H R 2000 Plasma Phys. Control. Fusion 42 R1 DOI:10.1088/0741-3335/42/1/201 [Cited within:1]
14 Leconte M, Diamond P H and Xu Y 2014 Nucl. Fusion 54 013004 DOI:10.1088/0029-5515/54/1/013004 [Cited within:1]
15 Willensdorfer M, Fable E, Wolfrum E, Aho-Mantila L, Aumayr F, Fischer R, Reimold F and Ryter F the ASDEX Upgrade Team 2013 Nucl. Fusion 53 093020 DOI:10.1088/0029-5515/53/9/093020 [Cited within:1]
16 Bourdelle C, Maggi C F, Chôné L, Beyer P, Citrin J, Fedorczak N, Garbet X, Loarte A, Millitello F, Romanelli M and Sarazin Y JET EFDA Contributors 2014 Nucl. Fusion 54 022001 DOI:10.1088/0029-5515/54/2/022001 [Cited within:1]
17 Ryter F, Barrera Orte L, Kurzan B, McDermott R M, Tardini G, Viezzer E, Bernert M and Fischer R The ASDEX Upgrade Team 2014 Nucl. Fusion 54 083003 DOI:10.1088/0029-5515/54/8/083003 [Cited within:1]
18 Xu G S, Wang H Q and Xu M 2014 Nucl. Fusion 54 103002 DOI:10.1088/0029-5515/54/10/103002 [Cited within:1]
19 Cziegler I, Tynan G R, Diamond P H, Hubbard A E, Hughes J W, Irby J and Terry J L 2014 Plasma Phys. Control. Fusion 56 075013 DOI:10.1088/0741-3335/56/7/075013 [Cited within:1]
20 Estrada T, Ascasíbar E, Blanco E, Cappa A, Diamond P H, Happel T, Hidalgo C, Liniers M, Ph van Milligen B, Pastor I and Tafalla D and the TJ-II Team 2012 Plasma Phys. Control Fusion 54 124024 DOI:10.1088/0741-3335/54/12/124024 [Cited within:1]
21 Miki K, Diamond P H, Hahn S H, Xiao W W, Gürcan Ö D and Tynan G R 2013 Phys. Plasmas 20 082304 DOI:10.1063/1.4818429 [Cited within:1]
22 Chôné L, Beyer P, Sarazin Y, Fuhr G, Bourdelle C and Benkadda S 2014 Phys. Plasmas 21 070702 DOI:10.1063/1.4890971 [Cited within:1]
23 Müller S H, Conway G D, Birkenmeier G, Carralero D, Happel T, Herrmann A, Manz P, de Marné P, Mlynek A, Müller H W, Potzel S, Rohde V, Stroth U, Tsalas M, Tynan G R and Wolfrum E ASDEX Upgrade Team 2014 Phys. Plasmas 21 042301 DOI:10.1063/1.4870012 [Cited within:1]
24 Stacey W M, Sayer M H, Floyd J P and Groebner R J 2013 Phys. Plasmas 20 012509 DOI:10.1063/1.4775601 [Cited within:1]
25 Battaglia D J, Chang C S and Kaye S M 2013 Nucl. Fusion 53 113032 DOI:10.1088/0029-5515/53/11/113032 [Cited within:1]
26 Tynan G R, Xu M, Diamond P H, Boedo J A, Cziegler I, Fedorczak N, Manz P, Miki K, Thakur S, Schmitz L, Zeng Z, Doyle E J, McKee G M, Yan Z, Xu G S, Wan B N, Wang H Q, Guo H Y, Dong J, Zhao K, Cheng J, Hong W Y and Yan L W 2013 Nucl. Fusion 53 073053 DOI:10.1088/0029-5515/53/7/073053 [Cited within:1]
27 Wu G J, Zhang X D, Li Y D, Sun P J and Cao G M 2014 Nucl. Fusion 54 083030 DOI:10.1088/0029-5515/54/8/083030 [Cited within:1]
28 Feng B B, Yao L H, Chen C Y, Ji X Q, Zhong W L, Shi Z B, Yu D L, Cui Z Y, Song X M and Duan X R 2013 Acta Phys. Sin. 62 015203 DOI:10.7498/aps.62.015203(in Chinese) [Cited within:1]
29 Du H L, Sang C F, Wang L, Sun J Z, Liu S C, Wang H Q, Zhang L, Guo H Y and Wang D Z 2013 Acta Phys. Sin. 62 245206 DOI:10.7498/aps.62.245206(in Chinese) [Cited within:1]
30 Weiland J 2012 Stability and Transport in Magnetic Confinement Systems New York Springer 1 [Cited within:5]
31 Weiland J 2014 Phys. Plasmas 21 122501 DOI:10.1063/1.4901597 [Cited within:3]
32 Rafiq T, Kritz A H, Weiland J, Pankin A Y and Luo L 2013 Phys. Plasmas 20 032506 DOI:10.1063/1.4794288 [Cited within:1]
33 Ma J, Wang G, Weiland J, Rafiq T and Kritz A H 2015 Phys. Plasmas 22 012304 DOI:10.1063/1.4905628 [Cited within:1]
34 Garzotti L, Garbe X, Mantica P, Parail V, Valovič M, Corrigan G, Heading D, Jones T T C, Lang P, Nordman H, Pégourié B, Saibene G, Spence J, Strand P and Weiland J contributors to the EFDA-JET Work programme 2003 Nucl. Fusion 43 1829 DOI:10.1088/0029-5515/43/12/025 [Cited within:1]
35 Weiland J, Crombe K, Mantica P, Naulin V and Tala T the JETEFDA Contributors 2011AIP Conference Proceedings- American Institute of Physics 1392 85 [Cited within:1]
36 Garzotti L, Garbet X, Mantica P and Parail V 2003 Nucl. Fusion 43 1829 DOI:10.1088/0029-5515/43/12/025 [Cited within:1]
37 Garbet X, Garzotti L and Mantica P 2003 Phys. Rev. Lett. 91 035001 DOI:10.1103/PhysRevLett.91.035001 [Cited within:1]
38 Waltz R E, Kerbel G O and Milovich J 1994 Phys. Plasmas 1 2229 DOI:10.1063/1.870934 [Cited within:1]
39 Zagorodny A and Weiland J 2009 Phys. Plasmas 16 052308 DOI:10.1063/1.3125306 [Cited within:1]
40 Staebler G M, Waltz R E and Wiley J C 1997 Nucl. Fusion 37 287 DOI:10.1088/0029-5515/37/3/I01 [Cited within:1]
41 Singh R and Weiland J 1999 Phys. Plasmas 6 1397 DOI:10.1063/1.873485 [Cited within:1]