Recent developments in the manipulation of cold or ultra-cold atoms offer a wide variety of applications, such as the new atomic frequency standards, ^{[1– 3]} the precision measurements of fundamental physics constants, ^{[4, 5]} new tests of fundamental theories of physics, ^{[6– 9]} etc.^{[10– 14]} The optical lattice trap with magic wavelength serves as a very useful tool, which could eliminate the Doppler and photon-recoil-related effects^{[15, 16]} and cancel the AC Stark shifts of the atomic transition levels, and then the transition frequency could be measured without the perturbations by the trapping field. This optical lattice approach proposed by Katori et al.^[15] can greatly improve the accuracy of the frequency standards based on cold atoms. In the past few years, the great achievements in Sr and Yb optical lattice clocks have been scored.^{[1, 2, 17– 20]} Some progress has also been made in the optical lattice clock based on cold Hg atoms, ^{[21, 22]} which seems to be the most competitive candidate for the next generation atomic frequency standard. Recently, different schemes of frequency standards based on optical lattices trapped cold atoms with magic wavelengths have been proposed, such as the cesium frequency standard, ^{[23, 24]} the optical frequency standards based on the cold gallium, dysprosium, aluminum, barium, ^{[25– 28]} etc.

In contrast to the great successes in the Sr and Yb optical clocks with the optical lattices trap, here we investigate the terahertz clock with the barium atoms in the optical lattice and ponder on the AC Stark shifts caused by the trapping field for the terahertz clock transitions. The terahertz clocks of the alkaline-earth atoms Mg and Ca with fine structure transition lines of the metastable triplet states were proposed in 1972^[29] and the terahertz clock based on the ³P₁– ³P₀ transition in the thermal Mg atoms beam was achieved in the mid-1990s.^{[30, 31]} Recently, the terahertz clock transitions of Sr, Ca, and Mg atoms were proposed to be used in the active optical clock^[32] and the possible magic wavelengths of trapping laser for these terahertz clock transitions of Sr, Ca, and Mg were calculated.^[33] The frequencies of these terahertz clock transitions correspond to a frequency region from 0.5 THz to 12.0 THz and the corresponding wavelength range (from 600 μ m to 25 μ m) fills the gap between the microwave clocks and the optical clocks.

Barium is a competitive candidate not only for the optical clocks but also for the terahertz clocks. There are three E2 (electric quadrupole) transitions^{[34, 35]} in barium atomic lines that could be used for the optical frequency standard. By contrast with other alkaline-earth metal atoms such as Sr, Ca, and Mg atoms, barium has some similar metastable triplet states 6s5d ³D_J (J = 1, 2, 3), the transition frequency (M1 transition) between the atomic levels 6s5d ³D₁ and 6s5d ³D₂ is about 5.4 THz and could also be used for the terahertz clocks. The laser cooling and trapping of barium atoms have also been achieved.^{[36, 37]} Furthermore, the barium atom is heavy which could contain the motional effects. In addition to the rather high frequency terahertz transition, the lifetimes of the states ³D₁ and ³D₂ (about tens of seconds) are more than sufficient, and studying a fine structure transition is interesting in the framework of a hypothetical drift of fundamental constants. In previous papers, ^{[27, 28, 38]} we have calculated the magic wavelengths for the optical clock transitions at 1085 nm, 877 nm, and 1107 nm of barium atoms in the optical lattice. In the present paper, we present the calculations of the AC Stark shifts and magic wavelengths for the terahertz clock transition between metastable triplet states ³D₁ and ³D₂ of barium atoms. Some other effects such as the collisional properties, the black-body radiation shifts, and the theoretical accuracy of the barium terahertz clock with optical lattice will be studied in the follow-up research.

There are two valence electrons in a Ba atom and the energy level diagram could be simplified as shown in Fig. 1. The transitions between the metastable states 6s5d D_J and the higher states could be chiefly divided into three groups: D_J– P_J′ , D_J– D_J′ , and D_J– F_J′ . The terahertz clock transition at 5.4 THz between D₁ and ³D₂ atomic levels and the optical clock transitions are also marked in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
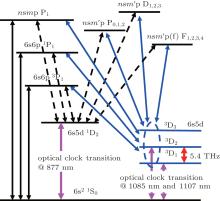	Fig. 1. Simplified energy level diagram of barium and some possible transitions between the metastable states and the higher atomic states.

Using the second-order perturbation theory, we could derive two sets of formulas to calculate the AC Stark shifts and both of them could lead to the same results. One way is to divide the total AC polarizability into two parts:^[39] the scalar polarizability α ₀ and the tensor polarizability α ₂. Here we use another set of formulas to carry out our calculation by following Refs. [40]– [42]. For the Zeeman sublevel m_i with energy E_i of the atomic state | i⟩ , the energy shift U_i(ω , p, m_i) caused by the trapping laser can be expressed as follows:

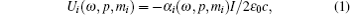
where α _i(ω , p, m_i) is the induced polarizability, v = ω /2π is the frequency of the trapping laser, I is the laser intensity, p is the laser polarization, ε ₀ is the dielectric constant, and c is the speed of light in the vacuum.

The induced polarizability α i(ω , p, m_i) can be calculated as follows:

where A_ki is the Einstein coefficients, and v_ik = ω _ik/2π = (E_k − E_i)/h is the transition frequencies (E_k > E_i). The large parentheses in the expression denote a 3J symbol. If the atomic data of ω _ik and A_ki are known, then the polarizability α _i and the magic wavelengths can be obtained by using Eq. (2).

The atomic data including the Einstein coefficients A_ki and the energy wave numbers (WNs) of the metastable triplet states ³D₁ and ³D₂ of barium are shown in Table 1. We select as many experimental results as possible from Refs. [43] and [44], and we choose the theoretical data from Refs. [45] and [46].

Table 1.

Table 1.

Table 1. Atomic transition data of the metastable triplet states 3D1 and 3D2 of Ba: level energy WNs (cm− 1) and Einstein coefficients between the fine structure states ∣ k⟩ and ∣ i⟩ Aki (106 s− 1). Lower state ∣ i⟩ Upper state ∣ k⟩ WN/cm− 1 Aik/106 s− 1 Refs. 6s5d 3D1 9033.966 cm− 1 6s7p1P1 32547.033 0.15 [46] 6s7p3P1 30815.512 2.65 [45] 6s7p3P0 30743.490 9.87 [45] 5d6p3P2 25956.519 14 [45] 5d6p3P1 25704.110 28 [43] 5d6p3P0 25642.126 80 [43] 5d6p3D2 24531.513 11.0 [43, 46] 5d6p3D1 24192.033 38.0 [43] 5d6p1D2 23074.387 11 [43, 46] 5d6p3F2 22064.645 15 [43, 46] 6s6p1P1 18060.261 0.0031 [43] 6s6p3P2 13514.745 0.01003 [45] 6s6p3P1 12636.623 0.1267 [45] 6s6p3P0 12266.024 0.35 [45] 6s5d 3D2 9215.501 cm− 1 6s7p1P1 32547.033 0.078 [45] 6s7p3P2 30987.240 1.6 [45] 6s7p3P1 30815.512 7.04 [45] 5d6p1P1 28554.221 0.090 [44] 5d6p1F3 26816.266 0.386 [45] 5d6p3P2 25956.519 16 [43] 5d6p3P1 25704.110 56 [43] 5d6p3D3 24979.834 11.6 [44, 45] 5d6p3D2 24531.513 33.0 [43] 5d6p3D1 24192.033 18.9 [43] 5d6p1D2 23074.387 0.065 [44] 5d6p3F3 22947.423 32 [43] 5d6p3F2 22064.645 7.6 [43] 6s6p1P1 18060.261 0.11 [43] 6s6p3P2 13514.745 0.1278 [45] 6s6p3P1 12636.623 0.315 [45]

Table 1. Atomic transition data of the metastable triplet states 3D1 and 3D2 of Ba: level energy WNs (cm− 1) and Einstein coefficients between the fine structure states ∣ k⟩ and ∣ i⟩ Aki (106 s− 1).

When carrying out our calculations, we assume the magnetic field to be zero and we also assume the trapping laser to have linear polarization, thus the effects of the magnetic field could be disregarded. We choose the boson isotope ¹³⁸Ba with the nuclear spin I = 0, thus the hyperfine structure^[47] would not be taken into account during our calculations.

Using the data listed in Table 1, we calculate the light shifts and obtain the magic wavelengths of the terahertz clock transition. Here we focus only on the magic wavelengths with negative light shift potentials and in our optical lattice scheme the atoms will be trapped at the higher laser intensity positions.

The wavelength-dependent light shifts for the sub-levels of 6s5d ³D₁ (m = 0) and 6s5d ³D₂ (m = 0, ± 1) of the linearly polarized trapping laser are shown in Fig. 2 and the magic wavelengths occur when the light shifts of atomic levels are equivalent as marked by the arrows. The laser intensity in our calculation is 10⁴ W/cm² and the unit of the light shifts is MHz. The wavelength range in our calculation is from 400 nm to 3000 nm and the magic wavelengths with negative light shift potentials only exist in a range from 600 nm to 800 nm. There are four magic wavelengths at 611.4 nm, 614.4 nm, 657.7 nm, and 780.7 nm respectively as shown in Fig. 2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Dependences of energy level shifts of the 6s5d 3D1 (m = 0) and 6s5d 3D2 (m = 0, ± 1) sub-levels on linearly polarized trapping laser wavelength. The arrows show the magic wavelength points with negative light shifts.

The induced light shifts of the ³D₁ (m = ± 1) sub-levels and ³D₂ (m = 0, ± 1, ± 2) sub-levels in the trapping laser field with wavelength λ are shown in Figs. 3(a)– 3(c). The ordinates are defined as those mentioned before. The arrows show the positions of the magic wavelengths with negative light shift at 648.3 nm, 671.7 nm, 672.6 nm, 782.1 nm, 976.2 nm, 1102.1 nm, 1107.2 nm, 1107.4 nm, 1166.7 nm, 1170.0 nm, and 2208.0 nm respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Wavelength-dependent atomic level shifts for the 6s5d 3D1 (m = 1) and 6s5d 3D2 (m = 0, ± 1, ± 2) of the linearly polarized trapping laser. The arrows show the magic wavelength points with negative light shifts.

The trap depth of the optical lattice, which is an important factor when trapping atoms in an optical lattice, is defined as the maximum temperature of the trapped atoms T = | U| /K_B, where U is the light shift potential (the AC Stark shift potential) and K_B is the Boltzmann constant. The trap depths would help us to choose suitable magic wavelengths to trapping atoms with an optical lattice. For example, the crossing at 648.3 nm has a trap depth of 2.55 μ K with a laser intensity of 10⁴ W/cm² as shown in Table 2, a quick calculation shows that this crossing would lead to about 15 recoil energies, therefore 648.3 nm is not a suitable working point. We calculate the trap depths of the linearly polarized optical lattice with different magic wavelengths.

Table 2.

Table 2.

Table 2. The AC Stark shift potential trap depths and slopes for different magic wavelengths with the 104 W/cm2 laser intensity. Magic wavelength/nm Corresponding clock transition AC Stark shift potential/MHz Trap depth/μ K Slope/(kHz/nm) 611.4 m = 0 → m′ = ± 1 – 1.1246 53.99 167.42 614.4 m = 0 → m′ = 0 – 0.8064 38.71 78.25 648.3 m = ± 1 → m′ = 0 – 0.0532 2.55 395.33 657.7 m = 0 → m′ = ± 1 – 0.4129 19.82 160.35 671.7 m = 1(− 1) → m′ = 1(− 1) – 1.0824 51.96 165.16 672.6 m = ± 1 → m′ = 0 – 1.0033 48.17 141.45 780.7 m = 0 → m′ = ± 1 – 1.3062 62.71 237.58 782.1 m = 1(− 1) → m′ = 1(− 1) – 1.0119 48.58 82.31 976.2 m = 1(− 1) → m′ = 2(− 2) – 0.2222 10.68 0.03 1102.1 m = 1(− 1) → m′ = 2(− 2) – 0.1766 8.48 0.38 1107.2 m = 1(− 1) → m′ = 1(− 1) – 0.1568 7.53 28.90 1107.4 m = ± 1 → m′ = 0 – 0.1504 7.22 60.21 1166.7 m = 1(− 1) → m′ = 1(− 1) – 0.1658 7.96 0.24 1170.0 m = ± 1 → m′ = 0 – 0.1652 7.93 0.28 2208.0 m = ± 1 → m′ = 0 – 0.0027 0.13 2.39

Table 2. The AC Stark shift potential trap depths and slopes for different magic wavelengths with the 104 W/cm2 laser intensity.

The slope of light shift difference is defined as k = d(Δ U)/dλ , where Δ U = ∣ U_j − U_i ∣ is the difference in AC Stark shift potential between the atomic levels. k shows the influence of the light shift difference caused by the laser wavelength or frequency perturbations. A strong slope should be refrained in the optical lattice traps because it would lead to a zero crossing for the differential polarizability. We also calculate the slopes of light shift difference for different magic wavelengths.

The results of the AC Stark shift potentials, trap depths, and slopes for different magic wavelengths are listed in Table 2. The laser intensity is 10⁴ W/cm² in our calculations. The corresponding clock transition of the magic wavelength is the transition from the Zeeman sub-level m of 6s5d ³D₁ to sub-level m′ of 6s5d ³D₂.

When building an optical lattice with magic wavelengths, the slopes should be smaller and the trap depths should be deeper. Commonly, the slopes are about 100 kHz/nm or less and the trap depths are about several μ K^{[48, 49]} or deeper. Using the data listed in Table 2, we could select some magic wavelengths possibly suitable for the optical lattice trap. The potentially magic wavelengths are 614.4 nm, 782.1 nm, 976.2 nm, 1102.1 nm, 1107.2 nm, 1107.4 nm, 1166.7 nm, and 1170.0 nm respectively. Because the slopes are very small, the trap depths are also deep enough for trapping atoms. The current lasers at these wavelengths are conveniently available.

In this study, we calculate the AC Stark shifts and the magic wavelengths with considering the terahertz clock transitions between 6s5d ³D₁ and 6s5d ³D₂ of barium. Our calculation is carried out with all the magnetic sub-levels. The trap depths and the slopes of light shift difference with different magic wavelengths are also calculated and appraised. The effects of the magnetic field are disregarded and the laser is assumed to be linearly polarized during our calculations. Based on the results of our calculation and discussion, we recommend several magic wavelengths such as 614.4 nm, 782.1 nm, 976.2 nm, 1102.1 nm, 1107.2 nm, 1107.4 nm, 1166.7 nm, and 1170.0 nm as potentially suitable working points for the optical lattice trapping laser. There is a long way to go for achieving a high-precision terahertz frequency standard and our results would be helpful for studying the terahertz frequency clocks.