Quantum entanglement not only provides possibilities to test quantum mechanics against local hidden theory, ^{[1– 4]} but also has practical applications in quantum information processing, such as quantum teleportation, ^[5] quantum cryptography, ^[6] and quantum dense coding.^[7] In general, these protocols require the maximally entangled state for the faithful transmission of quantum information. In the laboratory, it is very difficult to create perfect entanglement directly between two distant parties due to interaction with the environment. Thus it is necessary to develop the special technique of entanglement manipulation that can use local quantum operation and classical communication to transform previously shared less entangled pairs into a smaller number of highly entangled pairs. Multi-copy mixed state entanglement distillation for qubit pairs was proposed for this purpose^{[8– 15]} and similar schemes used for generating entangled qubits from arbitrary pure states are also studied.^{[16, 17]} Schemes for the purification of multi-qubits are also proposed.^{[18– 23]} But most of these schemes start from many identical qubit pairs in a Bell diagonal state shared by two separated parties, for non-Bell-diagonal initial states, two parties have to independently perform local operation on both members of each shared pair so as to transform the initial general mixed entangled state into Bell diagonal initial states.^{[9, 24]} More recently, the error threshold for measurement-based purification schemes and methods to overcome the noisy environment have also been studied.^{[25, 26]} On the other hand, although it was proved that one can distill a maximally entangled state from finite copies of a class of mixed entangled state, ^[27] the distinct scheme to purify a maximally entangled state is lacking.

In this paper, we propose a scheme for entanglement purification of a general mixed entangled state. In this scheme, we can obtain a smaller number of Bell diagonal states with higher entanglement from a large number of general mixed entangled states by using local operation and classical communication. In particular, we can directly obtain one maximally entangled state from two entangled pairs prepared in a class of mixed entangled state. Furthermore we propose a linear optical implementation of the present scheme with polarization beam splitters and photon detectors. Currently, experiments with polarization entanglement has opened a whole field of research. The photon polarization entanglement has also been used to implement some quantum information protocols like quantum teleportation, ^[28] dense coding, ^[29] and cryptography.^[30] A purification method for the polarization-entangled photon state is therefore of particular interest. Recently, several concentration and purification schemes have been proposed for the polarization-entangled photon state.^{[31, 32]} Pan et al. first proposed a purification scheme working for mixed polarization-entangled states.^[33] This scheme is only applied to purify mixed polarization-entangled states which are of the Werner form. Furthermore, two similar concentration schemes were proposed for concentrating the pure nonmaximally polarization-entangled state.^{[34, 35]} Our optical implementation scheme can be applied to purify a general mixed polarization-entangled state.

In order to present the principle idea of the purification scheme, we introduce simple building blocks shown in Fig. 1. Consider two pairs of particles (1, 2) and (3, 4) in a general mixed state

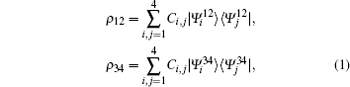
where

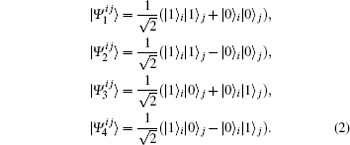
Alice holds particles 1 and 3 while Bob holds particles 2 and 4. Alice and Bob first perform a unitary operation | 0⟩ → | 1⟩ and | 1⟩ → | 0⟩ on particles 1 and 2, respectively. Then Alice and Bob each perform one quantum controlled-NOT operation | i⟩ | j⟩ → | i⟩ | i ⨁ j⟩ , where one pair ρ ₁₂ comprises the two controlled qubits and the other one ρ ₃₄ the two target qubits. Alice and Bob then measure the target qubits in the computational basis. If both target qubits are in the | 0⟩ state, two particles 1 and 2 are left in the state

with

and N = A + B + C + D. If both target qubits are not in the | 0⟩ state, both pairs are discarded. Based on the result of the measurement, the device shown in Fig. 1 can be used to delete the| Ψ ₁⟩ ⟨ Ψ ₂| , | Ψ ₂⟩ ⟨ Ψ ₁| , | Ψ ₃⟩ ⟨ Ψ ₄| , | Ψ ₄⟩ ⟨ Ψ ₃| , | Ψ ₁⟩ ⟨ Ψ ₄| , | Ψ ₄⟩ ⟨ Ψ ₁| and | Ψ ₂⟩ ⟨ Ψ ₃| , | Ψ ₃⟩ ⟨ Ψ ₂| terms of the state (1).

Next we demonstrate our purification scheme based on the building block shown in Fig. 1, which can be summarized as follows:

(i) Alice and Bob start with a number of identical qubit pairs in a general mixed state of the form (1). They perform the operation shown in Fig. 1 on the two shared pairs. Based on the measurement, they can obtain many copies of the state of the form (3).

(ii) Alice and Bob first perform a unitary operation on each pair of the form (3), then perform the operation shown in Fig. 1 on the two shared pairs. Thus they can obtain many identical Bell diagonal states of the form

with

(iii) Alice and Bob perform the operation shown in Fig. 1 on the two shared Bell diagonal states of the form (4). Based on the measurement, they can obtain the Bell diagonal state whose diagonal elements are given by

This map has been obtained in the procedure described in Ref. [10]. This demonstrates that we can start from a large number of general mixed states and end up, after local operation and classical communication, with a smaller number of Bell diagonal states with higher entanglement, i.e., our scheme can be directly applied to purify general mixed state. Next we demonstrate that our scheme can purify one maximally entangled state from a class of mixed entangled state of the form

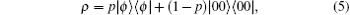
where

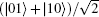
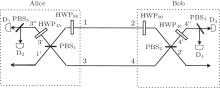
This state has been discussed in Ref. [27], in which it was proved that one can distill the maximally entangled state from two copies. However, the distinct scheme to purify maximally entangled state is lacking. If Alice and Bob perform an operation as shown in Fig. 1 on the joint state of the two pairs ρ ⊗ ρ , one can directly obtain the maximally entangled state with success probability 2p²α ²β ².

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The basic building block A of the purification scheme. P denotes a unitary operation | 0⟩ → | 1⟩ and | 1⟩ → | 0⟩ .

Next we propose a linear optical implementation of the setup shown in Fig. 2 with polarization beam splitters and photon detectors. The scheme is shown in Fig. 3. Here each quantum-controlled gate in Fig. 2 is replaced by polarization beam splitters. We now analyze the scheme in detail. Assume that Alice and Bob share two pairs of general mixed polarization-entangled photons ρ ₁₂⊗ ρ ₃₄ of the form (1). Here logical one state | 1⟩ is represented by horizontal polarization state | H⟩ and logical zero state | 0⟩ is represented by vertical polarization state | V⟩ . Alice holds photons 1 and 3, and Bob holds photon 2 and 4. As shown in Fig. 2, Alice and Bob first rotate the polarization of modes 1 and 2 by π /2 by using half-wave plate (HWP₉₀), respectively. After passing through the half-wave plates HWP₉₀, which transform | H⟩ → | V⟩ and | V⟩ → | H⟩ , Alice and Bob further forward photon 1 and 3, photon 2 and 4 to polarization beam splitters PBS₁ and PBS₂, respectively. The polarization beam splitter transmits the horizontal polarization and reflects the vertical polarization. Next Alice and Bob rotate the polarization of photon 3′ and 4′ by π /4 by two half wave plates HWP₄₅, respectively. 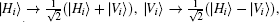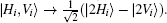The unitary transformation of half wave plate HWP₄₅ is given by and . Alice and Bob only consider the events in which one photon appears in the modes 3″ and 4″ and let the modes 3″ and 4″ pass through the polarization beam splitters PBS₃ and PBS₄ respectively, and observe the coincidence between either detectors D₁ and D₃, or D₂ and D₄. If D₁ and D₃ or D₂ and D₄ detect one photon respectively, the remaining two photons are transformed into the state of the form (3). Thus we proposed a linear optical implementation of the building blocks as shown in Fig. 1.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The complete quantum circuit of our scheme. A stands for the block in Fig. 1.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The linear optical implementation of the basic building blocks of the purification scheme. PBSi denote polarization beam splitters and HWP denote half-wave plate. Di is photon detector.

In summary, we presented a scheme for purification of a general mixed entangled state. In contrast to the scheme proposed in Refs. [9]– [11], our scheme starts from a general mixed entangled state and a Bell diagonal state can be directly obtained from many identical qubit pairs. We also showed that our scheme can purify one maximally entangled state from two pairs of a class of mixed entangled state. Finally we proposed a linear optical implementation of the scheme with polarization beam splitters and photon detectors. The scheme proposed in Ref. [33] is based on the post-selection method and only applied to purify the state of the Werner form. Our optical implementation of the scheme is not based on the post-selection method and can be applied to purify a general mixed polarization-entangled state, so that it is applicable to some quantum protocols designed for entangled quantum states without post-selection entanglement.