Weakly nonlinear multi-mode Bell–Plesset growth in cylindrical geometry

doi:10.1088/1674-1056/ab9c14

中国物理B ›› 2020, Vol. 29 ›› Issue (11): 115202-.doi: 10.1088/1674-1056/ab9c14

Hong-Yu Guo(郭宏宇)¹^,²^,†(), Tao Cheng(程涛)¹^,², Ying-Jun Li(李英骏)¹^,²^,^‡()

收稿日期:2020-04-26 修回日期:2020-06-07 接受日期:2020-06-12 出版日期:2020-11-05 发布日期:2020-11-03

Weakly nonlinear multi-mode Bell–Plesset growth in cylindrical geometry

Hong-Yu Guo(郭宏宇)^{1,2, †}, Tao Cheng(程涛)^1,2, and Ying-Jun Li(李英骏)^{1,2,, ‡}

1 State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining and Technology, Beijing 100083, China
2 School of Science, China University of Mining and Technology, Beijing 100083, China

Received:2020-04-26 Revised:2020-06-07 Accepted:2020-06-12 Online:2020-11-05 Published:2020-11-03
Contact: ^†Corresponding author. E-mail: ghy@cumtb.edu.cn ^‡Corresponding author. E-mail: lyj@aphy.iphy.ac.cn
Supported by:
the Fundamental Research Funds for the Central Universities, China (Grant No. 2019QS04), the National Natural Science Foundation of China (Grant No. 11574390), and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA 25051000).

摘要/Abstract

Abstract:

Bell–Plesset (BP) effect caused perturbation growth plays an important role in better understanding of characteristics of the convergence effect. Governing equations for multi-mode perturbation growth on a cylindrically convergent interface are derived. The second-order weakly nonlinear (WN) solutions for two-mode perturbations at the interface which is subject to uniformly radical motion are obtained. Our WN theory is consistent with the numerical result in terms of mode-coupling effect in converging Richtmyer–Meshkov instability. Nonlinear mode-coupling effects will cause irregular deformation of the convergent interface. The mode-coupling behavior in convergent geometry depends on the mode number, Atwood number A and convergence ratio C_r. The A = –1.0 at the interface results in larger perturbation growth than A = 1.0. The growth of generated perturbation modes from two similar modes at the initial stage are smaller than that from two dissimilar modes.

Key words: Bell-Plesset effect, Rayleigh-Taylor instability, inertial confinement fusion

Hong-Yu Guo(郭宏宇), Tao Cheng(程涛), Ying-Jun Li(李英骏). [J]. 中国物理B, 2020, 29(11): 115202-.

Hong-Yu Guo(郭宏宇), Tao Cheng(程涛), and Ying-Jun Li(李英骏). Weakly nonlinear multi-mode Bell–Plesset growth in cylindrical geometry[J]. Chin. Phys. B, 2020, 29(11): 115202-.

图/表 6

参考文献 30

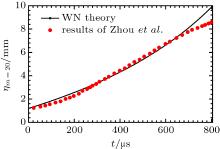
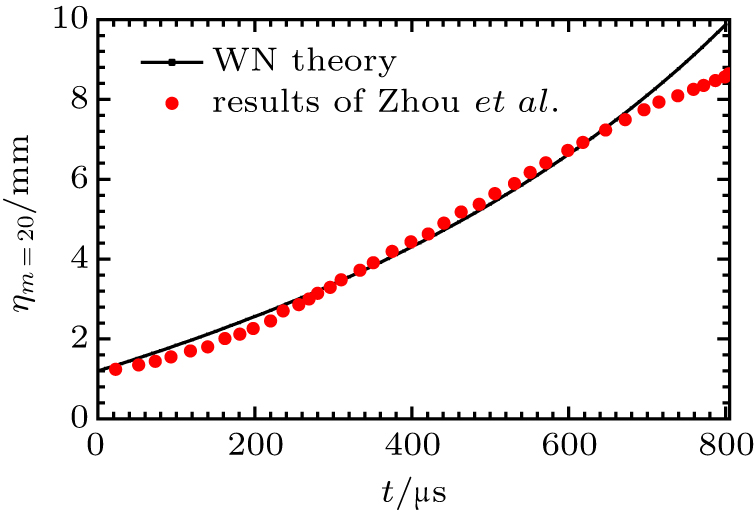
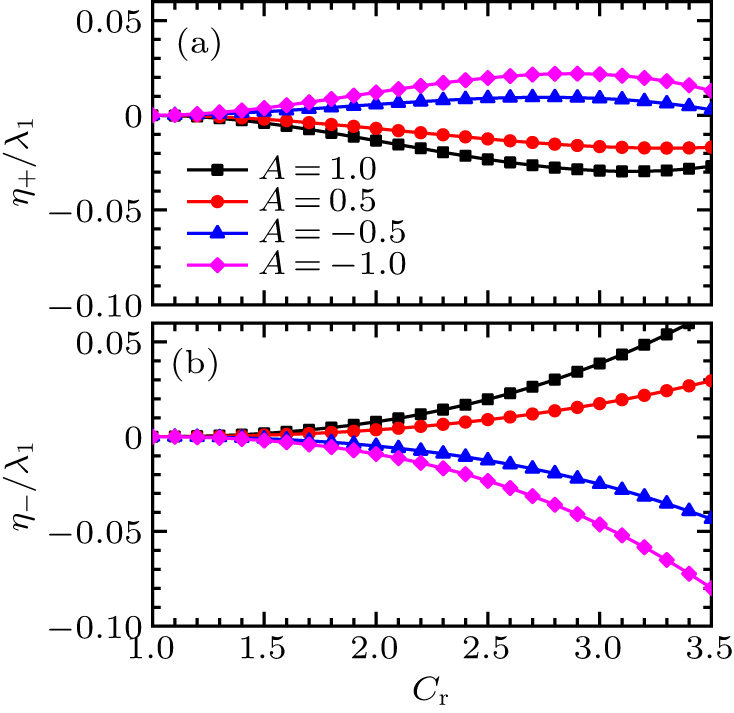
[1]	Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339 DOI: 10.1063/1.1578638
[2]	Wang L F, Ye W H, He X T, Wu J F, Fan Z F, Xue C, Guo H Y, Miao W Y, Yuan Y T, Dong J Q, Jia G, Zhang J, Li Y J, Liu J, Wang M, Ding Y K, Zhang W Y 2017 Sci. China Phys. Mech. Astron. 60 055201 DOI: 10.1007/s11433-017-9016-x
[3]	Remington B A, Drake R P, Ryutov D D 2006 Rev. Mod. Phys. 78 755 DOI: 10.1103/RevModPhys.78.755
[4]	Craxton R S et al. 2015 Phys. Plasmas 22 110501 DOI: 10.1063/1.4934714
[5]	Marocchino A, Atzeni S, Schiavi A 2010 Phys. Plasmas 17 112703 DOI: 10.1063/1.3505112
[6]	Rayleigh L 1882 Proc. London Math. Soc. s1–14 170 DOI: 10.1112/plms/s1-14.1.170
[7]	Taylor G 1950 Proc. R. Soc. Lond. A 201 192 DOI: 10.1098/rspa.1950.0052
[8]	Bell G I 1951 Los Alamos Scientific Laboratory Report No. LA-1321
[9]	Plesset M S 1954 J. Appl. Phys. 25 96 DOI: 10.1063/1.1721529
[10]	Hsing W W, Barnes C W, Beck J B, Hoffman N M, Galmiche D, Richard A, Edwards J, Graham P, Rothman S, Thomas B 1997 Phys. Plasmas 4 1832 DOI: 10.1063/1.872326
[11]	Hsing W W, Hoffman N M 1997 Phys. Rev. Lett. 78 3876 DOI: 10.1103/PhysRevLett.78.3876
[12]	Amendt P, Colvin J D, Ramshaw J D, Robey H F, Landen O L 2003 Phys. Plasmas 10 820 DOI: 10.1063/1.1543926
[13]	Wang X G, Sun S K, Xiao D L et al. 2019 Chin. Phys. B 28 035201 DOI: 10.1088/1674-1056/28/3/035201
[14]	Zhai Z G et al. 2018 Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 232 2830 DOI: 10.1177/0954406217727305
[15]	Ding J C et al. 2017 Phys. Rev. Lett. 119 014501 DOI: 10.1103/PhysRevLett.119.014501
[16]	Epstein R 2004 Phys. Plasmas 11 5114 DOI: 10.1063/1.1790496
[17]	Velikovich A L, Schmit P F 2015 Phys. Plasmas 22 122711 DOI: 10.1063/1.4938272
[18]	Guo H Y et al. 2017 Phys. Plasmas 24 112708 DOI: 10.1063/1.5001533
[19]	Guo H Y, Wang L F, Ye W H, Wu J F, Zhang W Y 2018 Chin. Phys. B 27 055205 DOI: 10.1088/1674-1056/27/5/055205
[20]	Zhang J, Wang L F, Ye W H, Wu J F, Guo H Y, Zhang W Y, He X T 2017 Phys. Plasmas 24 062703 DOI: 10.1063/1.4984782
[21]	Wang L F, Wu J F, Ye W H, Zhang W Y, He X T 2013 Phys. Plasmas 20 042708 DOI: 10.1063/1.4803067
[22]	Wang L F, Wu J F, Guo H Y, Ye W H, Liu J, Zhang W Y, He X T 2015 Phys. Plasmas 22 082702 DOI: 10.1063/1.4928088
[23]	Guo H Y, Wang L F, Ye W H, Wu J F, Zhang W Y 2018 Chin. Phys. Lett. 35 055201 DOI: 10.1088/0256-307X/35/5/055201
[24]	Haan S W 1991 Phys. Fluids B 3 2349 DOI: 10.1063/1.859603
[25]	Xin J, Yan R, Wan Z H, Sun J, Zheng J, Zhang H, Aluie H R., Betti R 2019 Phys. Plasmas 26 032703 DOI: 10.1063/1.5070103
[26]	Zhou Z B, Ding J C, Zhai Z G, Wan C, Luo X S 2019 Acta Mech. Sin. DOI: 10.1007/s10409-019-00917-3
[27]	Weber C R, Clark D S, Cook A W et al. 2015 Phys. Plasmas 22 032702 DOI: 10.1063/1.4914157
[28]	Clark D S, Marinak M M, Weber C R et al. 2015 Phys. Plasmas 22 022703 DOI: 10.1063/1.4906897
[29]	Mikaelian K O 2005 Phys. Fluids 17 094105 DOI: 10.1063/1.2046712
[30]	Sauppe J P, Haines B M, Palaniyappan S, Bradley P A, Batha S H, Loomis E N, Kline J L 2019 Phys. Plasmas 26 042701 DOI: 10.1063/1.5083851

Weakly nonlinear multi-mode Bell–Plesset growth in cylindrical geometry

RichHTML

PDF (PC)

赞

可视化

摘要/Abstract

引用本文

使用本文

图/表 6

参考文献 30

相关文章 0

Metrics

本文评价

推荐阅读 0