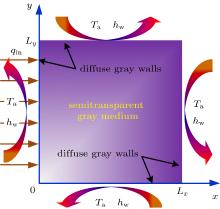
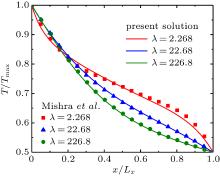
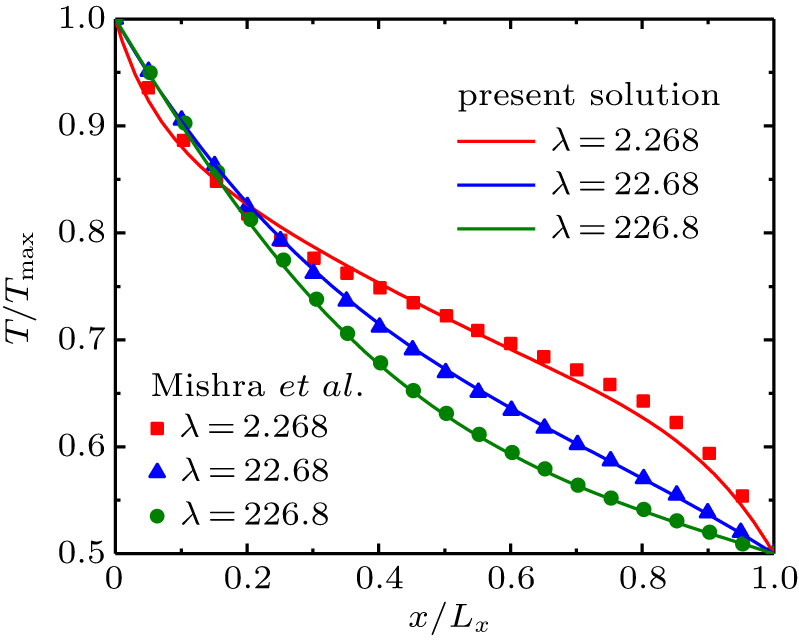
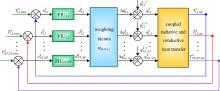
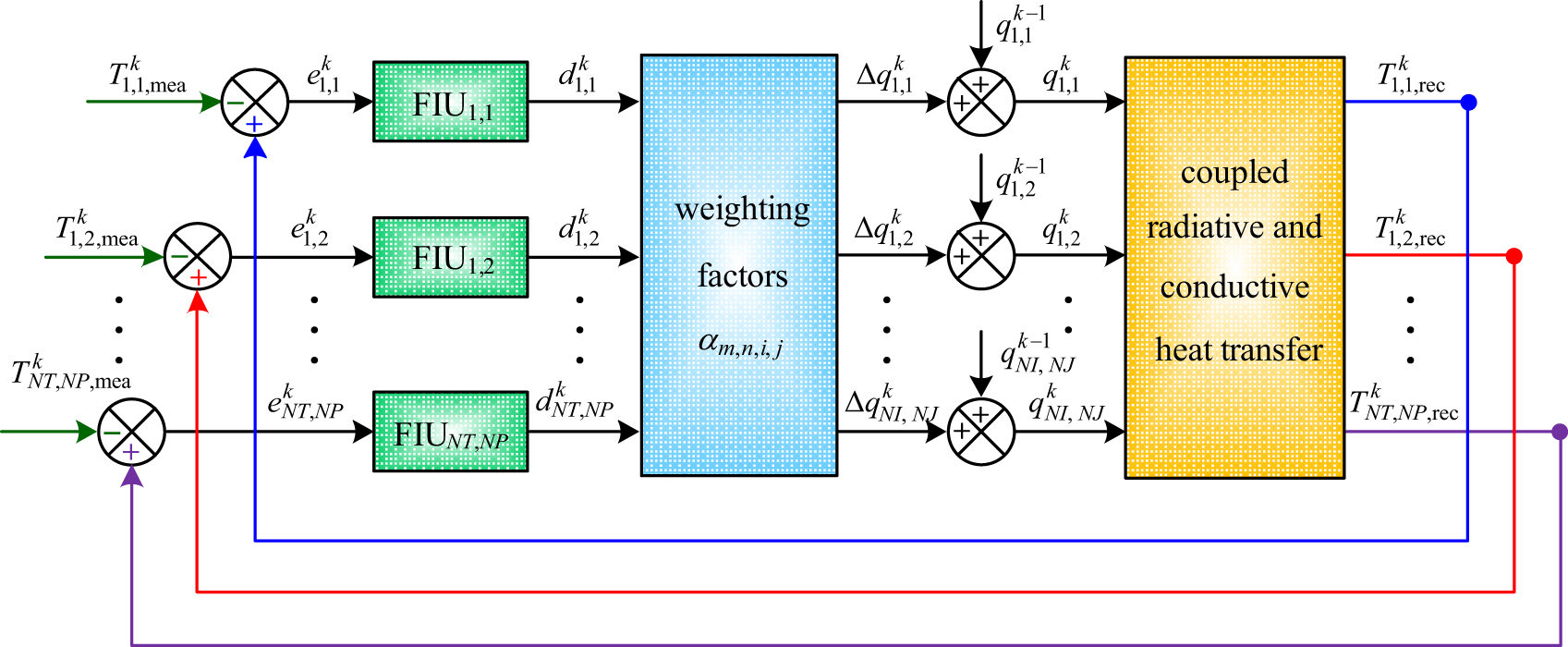
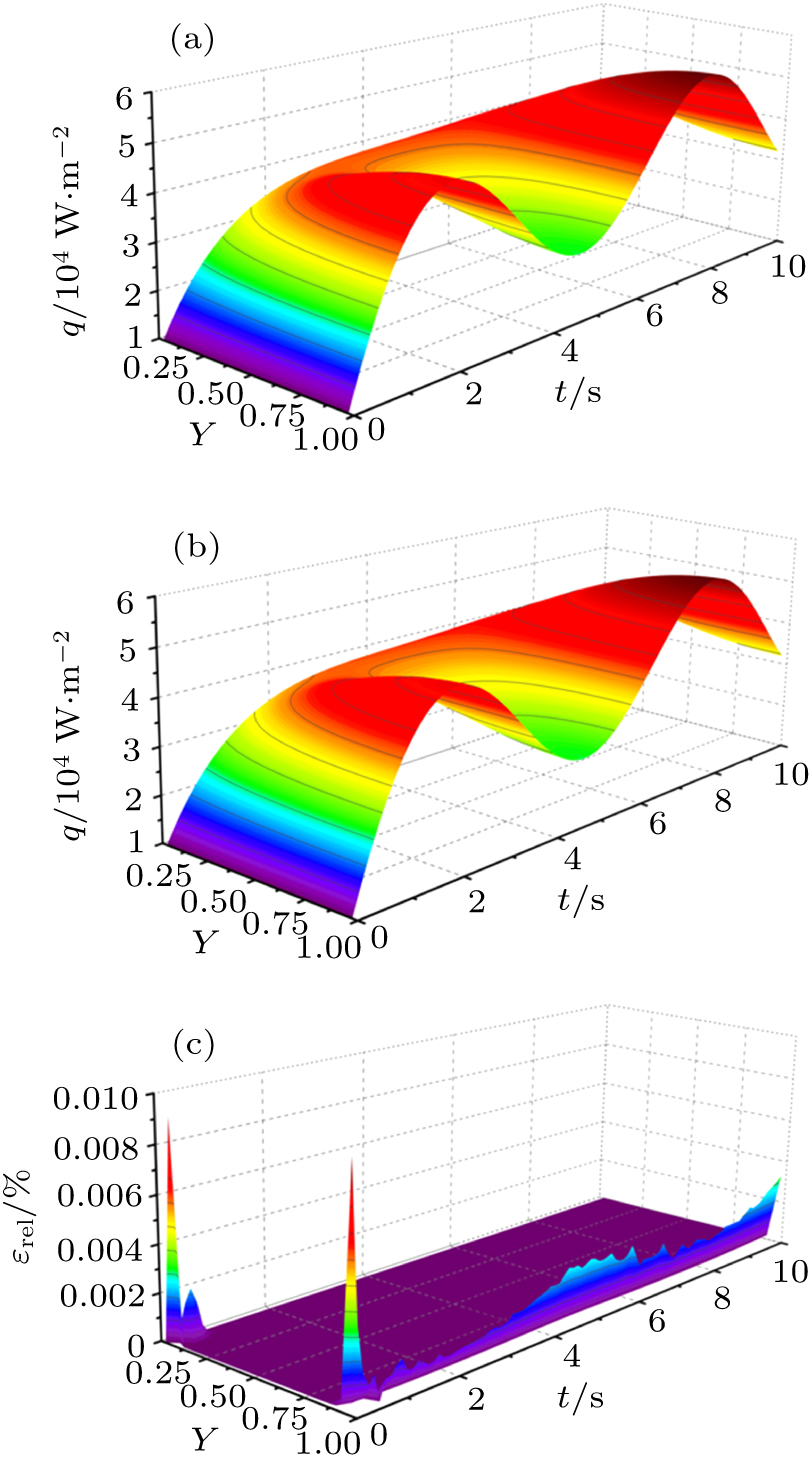
中国物理B ›› 2020, Vol. 29 ›› Issue (11): 110202-.doi: 10.1088/1674-1056/aba608
Shuang-Cheng Sun(孙双成)1,2,†( ), Guang-Jun Wang(王广军)1,2, Hong Chen(陈红)1,2
), Guang-Jun Wang(王广军)1,2, Hong Chen(陈红)1,2
An efficient inverse approach for reconstructing time- and space-dependent heat flux of participating medium
Shuang-Cheng Sun(孙双成)1,2, †, Guang-Jun Wang(王广军)1,2, and Hong Chen(陈红)1,2$
- 1 School of Energy and Power Engineering, Chongqing University, Chongqing 400044, China
2 Key Laboratory of Low-grade Energy Utilization Technologies and Systems, Ministry of Education, Chongqing University, Chongqing 400044, China