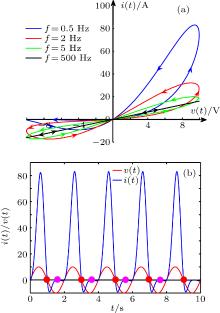
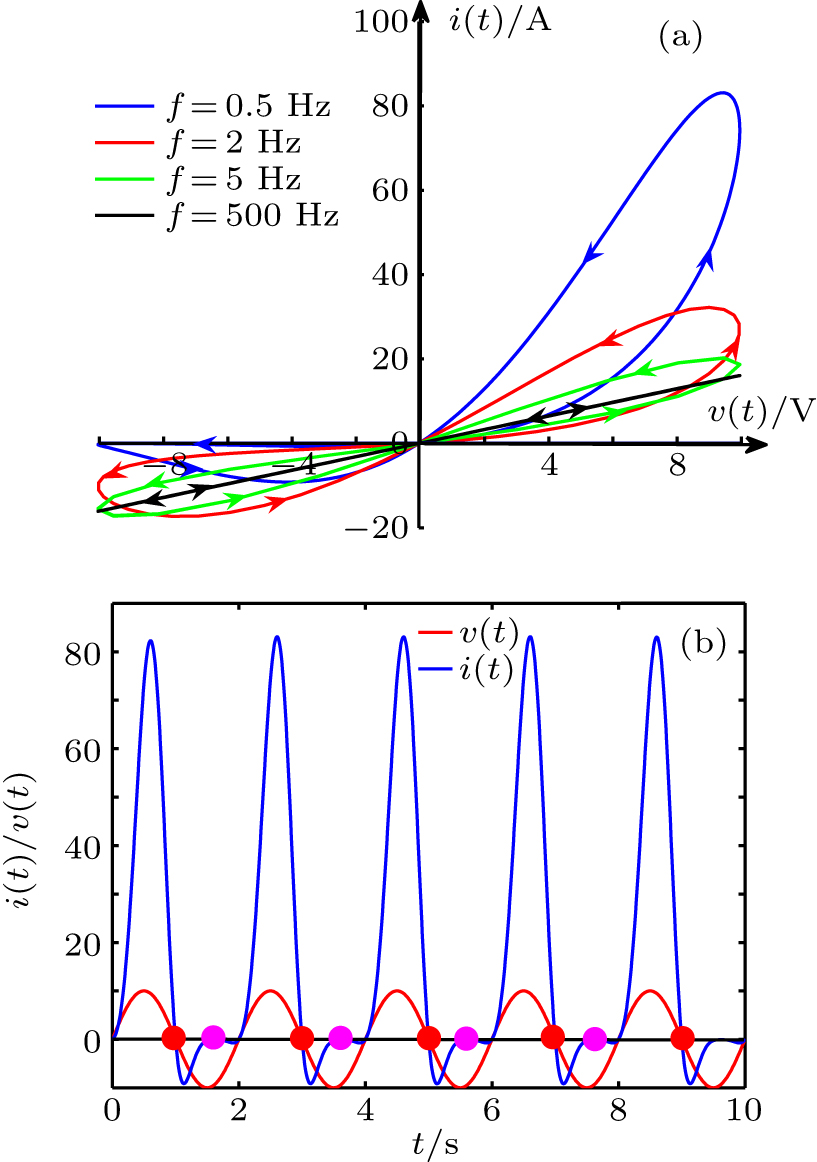
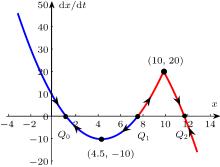
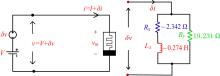
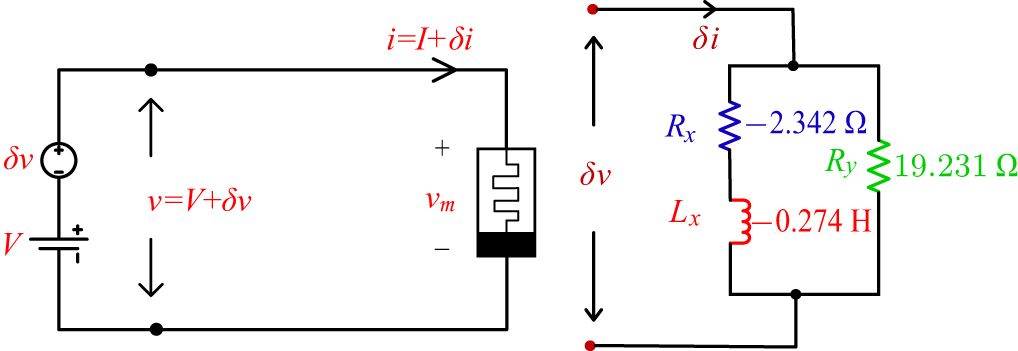
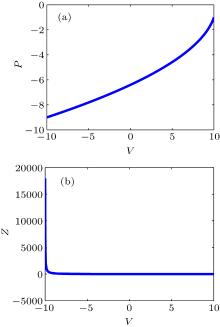
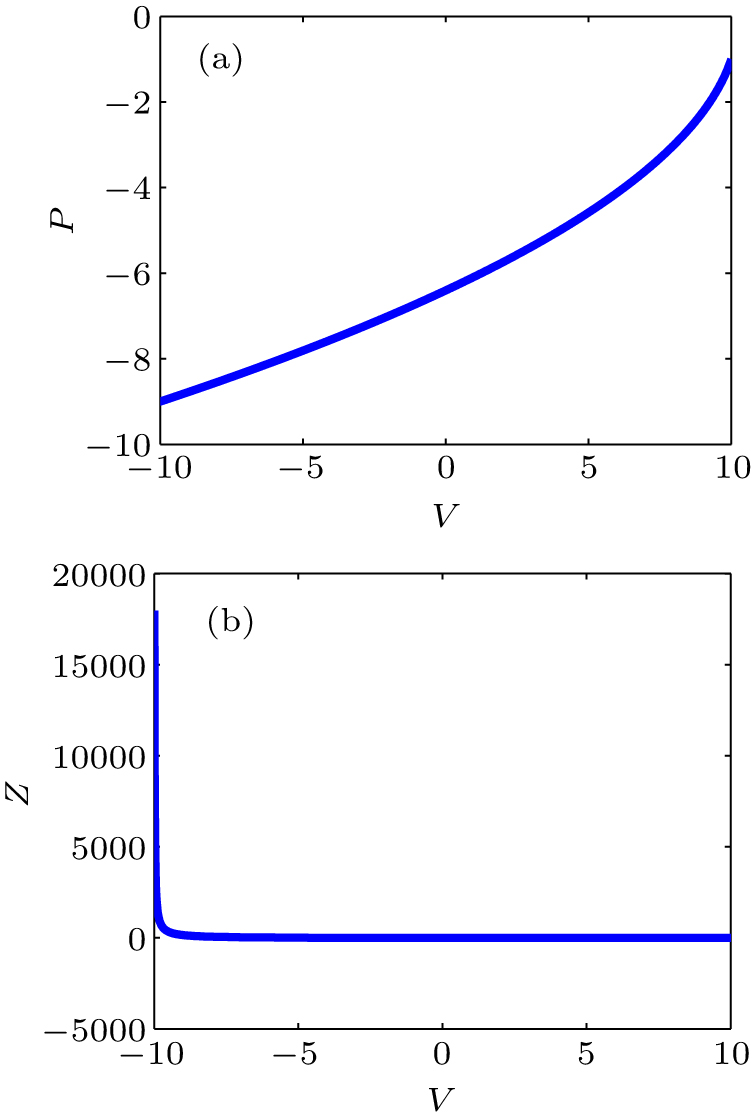
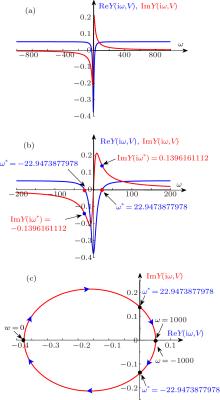
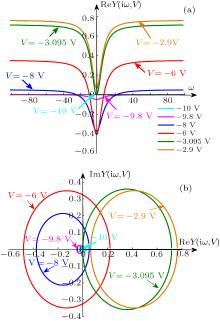
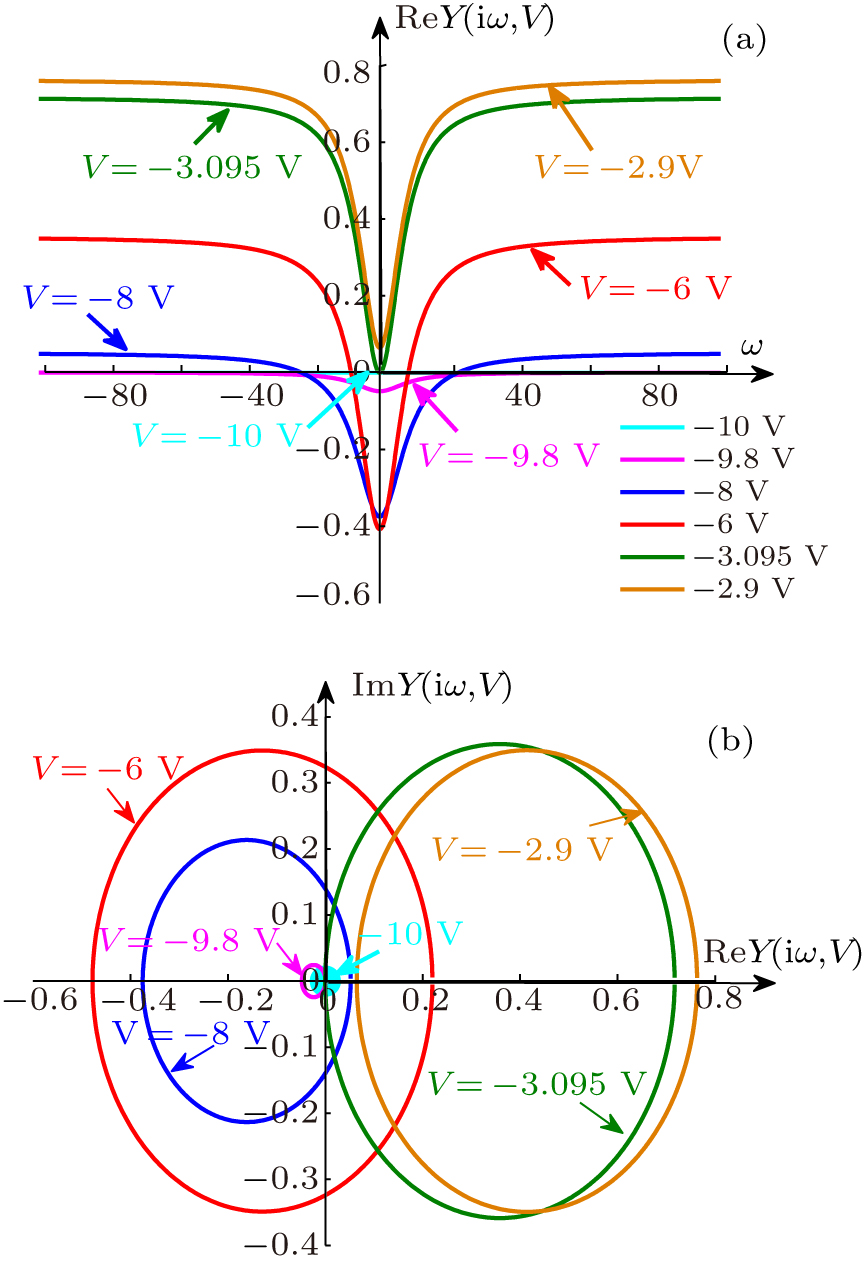
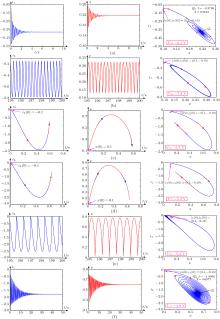
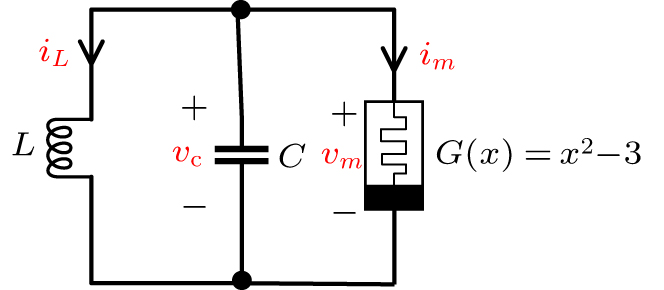
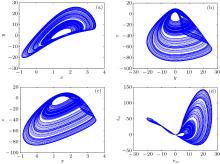
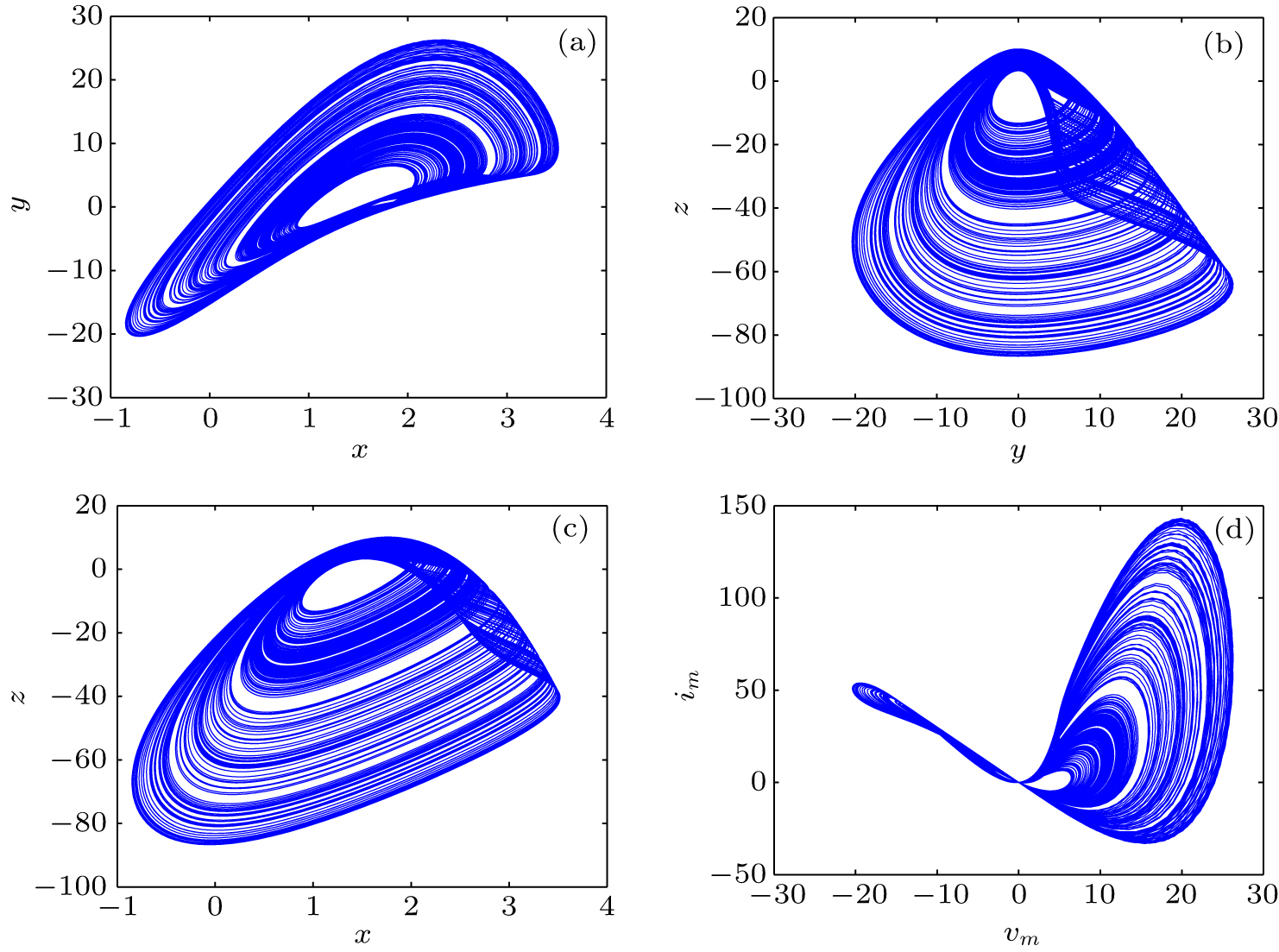
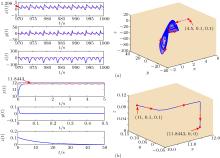
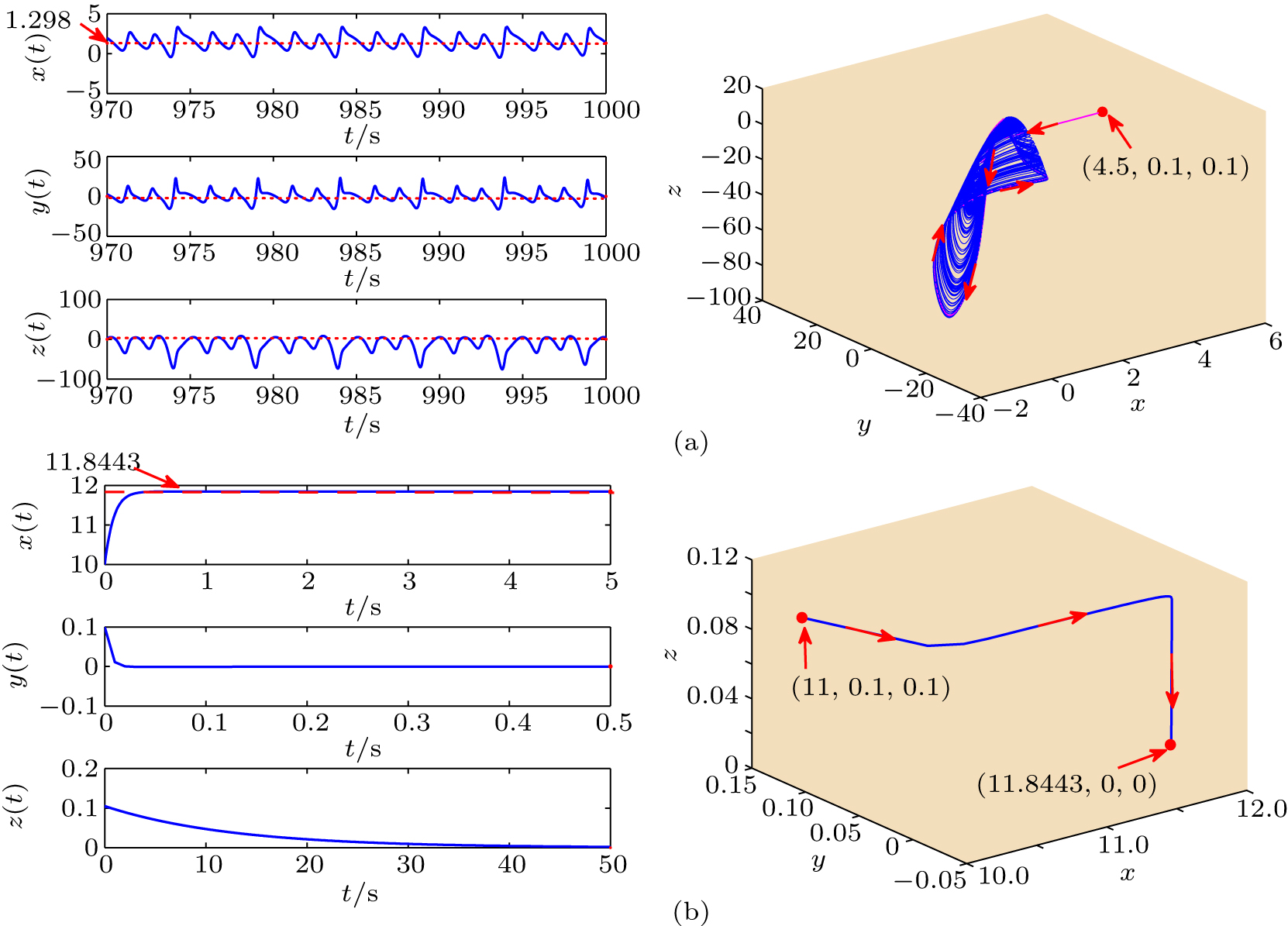
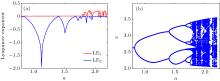
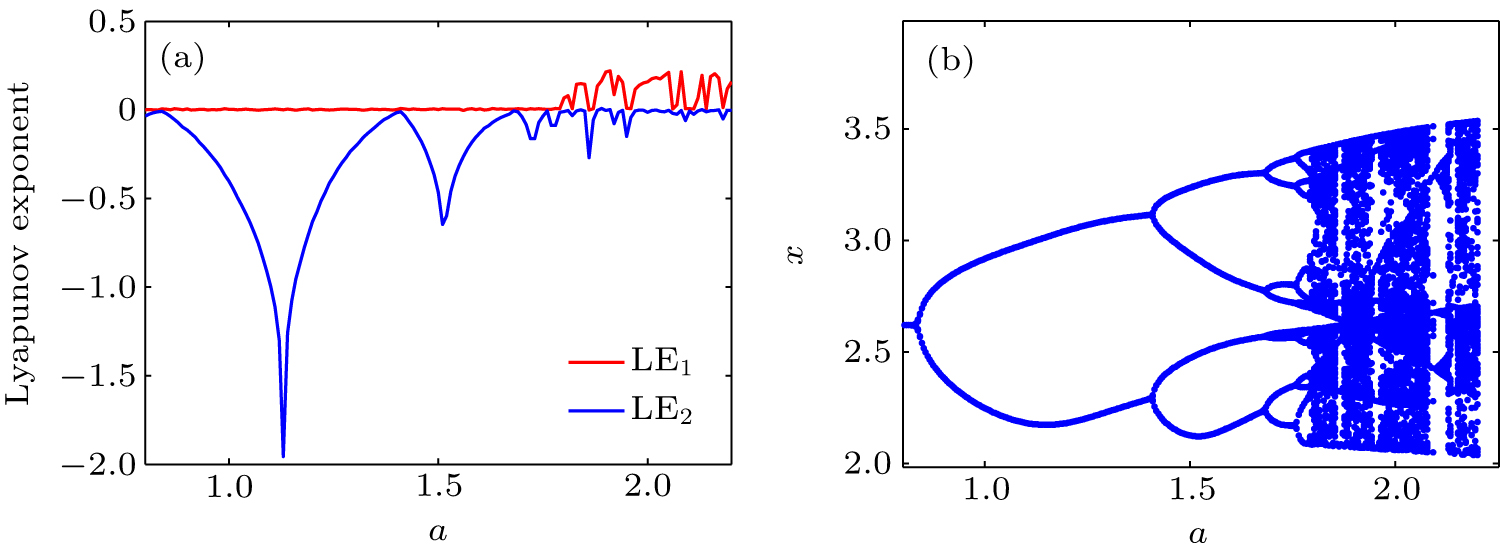
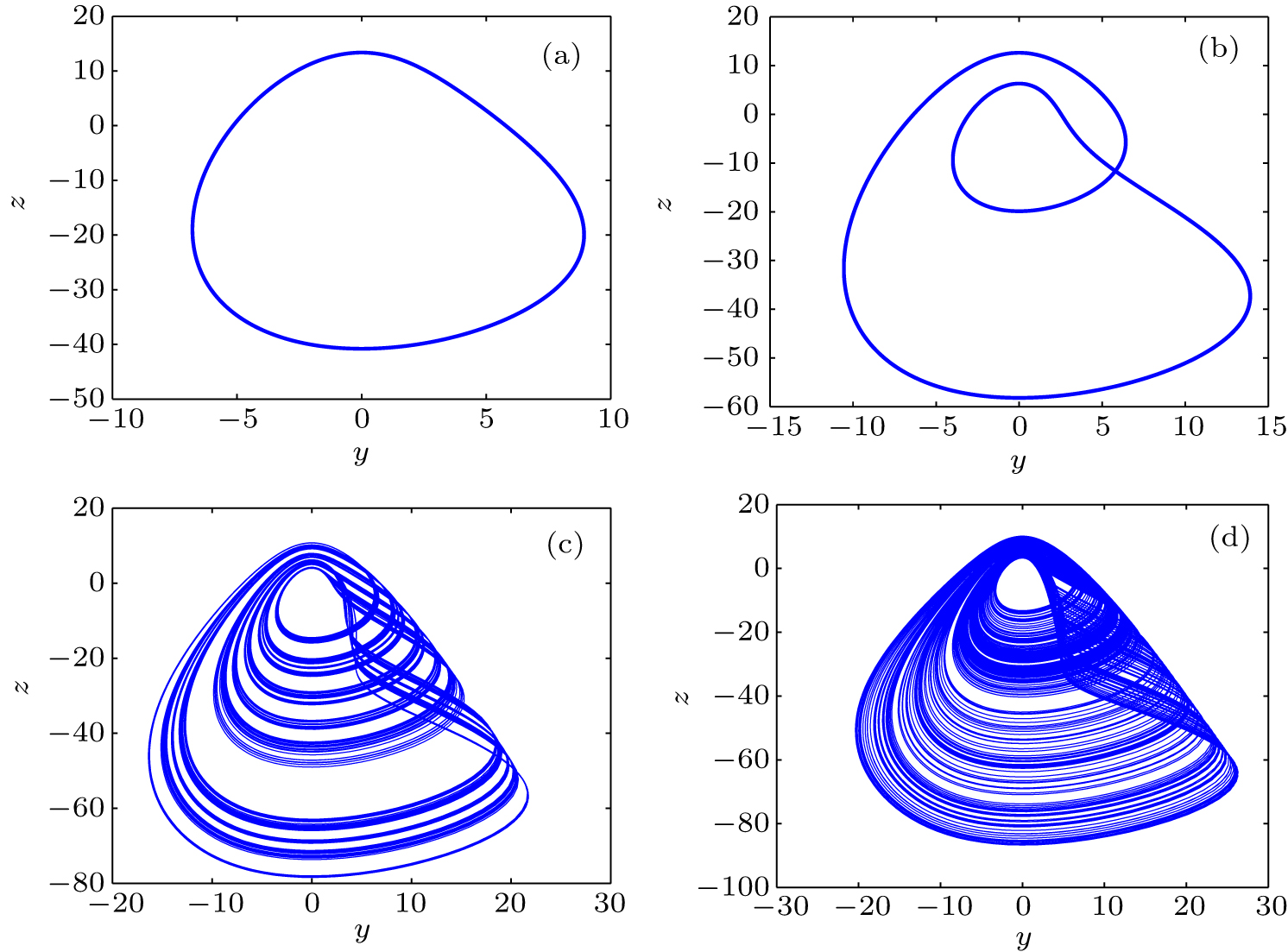
中国物理B ›› 2020, Vol. 29 ›› Issue (11): 110503-.doi: 10.1088/1674-1056/ab9ded
Wen-Yu Gu(谷文玉)1, Guang-Yi Wang(王光义)1,†( ), Yu-Jiao Dong(董玉姣)1, Jia-Jie Ying(应佳捷)1
), Yu-Jiao Dong(董玉姣)1, Jia-Jie Ying(应佳捷)1
Nonlinear dynamics in non-volatile locally-active memristor for periodic and chaotic oscillations
Wen-Yu Gu(谷文玉), Guang-Yi Wang(王光义)†, Yu-Jiao Dong(董玉姣), and Jia-Jie Ying(应佳捷)
- Institute of Modern Circuits and Intelligent Information, Hangzhou Dianzi University, Hangzhou 310018, China