Cite this Article
Du Qian, Lan Kang, Zhang Yan-Hui, Jiang Lu-Jing. Geometric phase of an open double-quantum-dot system detected by a quantum point contact. Chinese Physics B, 2020, 29(3): 030302  
Permissions
Geometric phase of an open double-quantum-dot system detected by a quantum point contact
Du Qian, Lan Kang, Zhang Yan-Hui †, Jiang Lu-Jing
School of Physics and Electronics, Shandong Normal University, Jinan 250014, China

 

† Corresponding author. E-mail: yhzhang@sdnu.edu.cn

Project supported by the Natural Science Foundation of Shandong Province, China (Grant No. ZR2014AM030).

Abstract

We study theoretically the geometric phase of a double-quantum-dot (DQD) system measured by a quantum point contact (QPC) in the pure dephasing and dissipative environments, respectively. The results show that in these two environments, the coupling strength between the quantum dots has an enhanced impact on the geometric phase during a quasiperiod. This is due to the fact that the expansion of the width of the tunneling channel connecting the two quantum dots accelerates the oscillations of the electron between the quantum dots and makes the length of the evolution path longer. In addition, there is a notable near-zero region in the geometric phase because the stronger coupling between the system and the QPC freezes the electron in one quantum dot and the solid angle enclosed by the evolution path is approximately zero, which is associated with the quantum Zeno effect. For the pure dephasing environment, the geometric phase is suppressed as the dephasing rate increases which is caused only by the phase damping of the system. In the dissipative environment, the geometric phase is reduced with the increase of the relaxation rate which results from both the energy dissipation and phase damping of the system. Our results are helpful for using the geometric phase to construct the fault-tolerant quantum devices based on quantum dot systems in quantum information.

PACS: ;03.65.Vf;;03.65.Yz;;05.60.Gg;
Keyword:;geometric phase;;decoherence;;quantum transport;
1. Introduction

The quantum state, after undergoing adiabatic and cyclic evolution, acquires a phase that contains a component which is only related to the geometry of the path traced by the system called the geometric phase.[1] The conception of geometric phase has been extended to diverse directions.[2–5] In the realistic implementations of quantum computation, it is necessary to consider the environmental effect on the evolution of the quantum systems, which is driven by the coupling of the system and the surrounding environments.[6–17] Moreover, the experiments about the geometric phase have proved that its intrinsic fault-tolerate feature is significant for implementing quantum information processing.[18–34] Thus, it is important to study the geometric phase in different environments for investigating quantum phase transition, quantum error correction, and so on.

With the rapid development of quantum information, a large amount of attention has been focused on exploiting the feasible programs so as to develop quantum computing. In these schemes, the double-quantum-dot (DQD) system is a promising candidate in quantum information processing on account of its long coherent time and powerful controllability.[35–39] Meanwhile, the quantum point contact (QPC) is widely used to measure the transport properties of electrons due to its high sensitivity. The extensive theoretical and experimental works associated with it have been done,[40–43] which has inspired us to study further the physical phenomenon in the quantum dot system.

The study of the geometric phase in different situations has made great progresses,[44–65] such as a two-level system coupled to a radiation field at zero temperature[66] and a spin-1/2 particle interacting with N independent spins.[67] There are also many achievements on the geometric phase of the quantum dot systems, including the influence of the temperature on the geometric phase in two coupled quantum dots[68] and the current method to obtain the geometric phase in the DQD system.[69,70] The geometric phase of the DQD system measured by a single-electron transistor (SET) has been reported, in which an electron inside the quantum dot of the SET would cause the fluctuations in the coupling strength between the quantum dots and the energy level in the nearest quantum dot.[71–75] However, there are still many valuable questions in the study of the geometric phase in quantum dot systems. For example, when we use the QPC as a detector, how the geometric phase of the DQD system evolves during a quasiperiod in the pure dephasing or dissipative environment and what is the physical mechanism of the QPC and the environmental effect on it? Solving these questions provides some reference for taking advantage of the DQD systems to construct geometric quantum logic gates.

In this paper, we employ the QPC as a detector to study the properties of the geometric phase in a DQD system and then analyze its effect on the geometric phase. We calculate the geometric phase of the DQD system coupled to a QPC in two kinds of environments according to the Bloch-type rate equations and the kinematic approach of the geometric phase given in mixed states under nonunitary evolution. It is shown that the coupling strength between the two quantum dots has an enhancement on the geometric phase. Moreover, there is a notable near-zero region in the geometric phase due to the coupling between the system and the QPC. Additionally, the influences of the pure dephasing environment and the dissipative environment on the geometric phase are analyzed. The geometric phase is reduced with the increase of the dephasing rate which is generated only by the phase damping of the system in the pure dephasing environment. In the dissipative environment, the geometric phase decreases as the relaxation rate increases, which results from both the energy dissipation and phase damping of the system.

2. Theoretical framework

We consider a DQD system measured by a QPC as shown in Fig. 1. The Hamiltonian of this model, H, is given by

where HS represents the Hamiltonian of the DQD system. We assume that only one electron can occupy the DQD system due to the strong inner and interdot Coulomb repulsions and there is also only one energy level in each quantum dot El,r[76] with Er −El = ε. Ω and stand for the coupling strength between the two quantum dots and the creation (annihilation) operator of electrons in the DQD, respectively. The Hamiltonian for the QPC is expressed as HPC, where is the creation (annihilation) operator of the left and right reservoirs and Eα,β is the left and right reservoir states in the QPC. Ωαβ represents the hopping amplitude between states Eα and Eβ of the QPC. The last term HI describes the interaction between the DQD system and the QPC, which leads to a change in the hopping amplitude of the QPC, , due to the location of the electron in the DQD. When the electron oscillates from the left quantum dot to the right quantum dot, the tunneling barrier of the QPC changes, causing the hopping amplitude to change from Ωαβ to . Eventually, there is a variation in the current through the QPC. Thereby, the QPC can measure sensitively which quantum dot the electron is in.

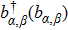
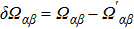
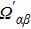
Fig. 1. The model of the DQD system coupled with a QPC. The chemical potentials of the left and right reservoirs are μα, μβ and μα > μβ.

The dynamical evolution of the reduced density matrix for the system satisfies the Liouville equation

where the first term on the right-hand side describes the unitary evolution of the system and the second term represents the decoherence caused by the interaction of the system coupled to a detector and the environments.

Firstly, we consider that the DQD system is only coupled to the QPC, and the evolution of the reduced density matrix elements of the electron is written as[40]

where ρll(t) + ρrr(t) = 1, and . The diagonal terms ρll(t) and ρrr(t) are the probabilities of finding the electron in the left or right quantum dot, respectively. The off-diagonal terms ρlr(t) and ρrl(t) have an exponential decay with the decoherence rate , which is caused by the effect of the QPC. , , where ρα and ρβ are the densities of states in the reservoirs. When t → ∞, the reduced density matrix is in the statistical mixture, .

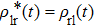
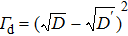
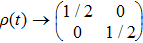
Given that this DQD system is an open system which is affected by the QPC and the environments, the formulation of the geometric phase in the mixed states under nonunitary evolution is used[5]

where εk(t) and ϕk(t) are the corresponding k-th eigenvalues and eigenvectors of the reduced density matrix ρ(t) in the DQD system, and τ is the time after the system completes a cyclic evolution when it is not affected by the environments. However, as the system is open due to the external influences, we define a quasiperiod , where is the frequency at which the electron oscillates between the two dots.

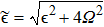
The instantaneous eigenvalues of the reduced density matrix are given by

Correspondingly, the time-dependent eigenvectors are expressed as

with the coefficients

For simplicity, we consider the condition where the system is prepared in a pure initial state with , . Obviously, ε1(0) = 1, ε2(0) = 0 and hence |ϕ2(t)⟩ does make no sense for the geometric phase. We substitute Eqs. (5)–(7) into Eq. (4) and finally the geometric phase γg is written as

To associate with the geometric feature of the evolution, we can express ρ(t) in the Bloch sphere representation as , where σ = (σx, σy, σz) is the vector of Pauli matrices and r(t) = (rx(t), ry(t), rz(t)) is the Bloch vector with[50]

When ρ(t) is a pure state, |r(t)| = 1; whereas as |r(t)| < 1, it represents a mixed state. Based on the above initial condition, the eigenvalues and time-dependent eigenvectors which contribute to the geometric phase are expressed as

Then the geometric phase in Eq. (8) can be rewritten as

3. Results and discussion

In this section, we will discuss the properties of the geometric phase of the DQD system when we use a QPC as a detector in the presence of two kinds of environments, namely, the pure dephasing and dissipative environments, and investigate numerically the influences of the detector and these two environments on the phase.

3.1. Geometric phase in the pure dephasing environment

Firstly, we consider only the interaction between the DQD system and the pure dephasing environment. Then we use the rotation operation, , , θ = arctan(2Ω/ε), to diagonalize the system's Hamiltonian.[40,77,78] As a result, with and this system is transformed into a parallel two-level system. The corresponding reduced density matrix is presented as[41]

From this equation, we can see that in the pure dephsing environment, the off-diagonal terms of the system are destroyed and finally disappear due to the damping of the phase with the dephasing rate Γϕ, whereas the diagonal terms remain in the initial state. Then together with the role of the QPC, we return to the initial basic states and the reduced density matrix ρ(t) is written by tracing out both the QPC and the pure dephasing environment from the entire system. According to Ref. [41], the elements of the reduced density matrix satisfy

We calculate the numerical results of the geometric phase γg during a quasiperiod τ according to Eqs. (8) and (13).

Figure 2 shows that the geometric phase γg increases with the coupling strength Ω for different decoherence rate Γd and finally tends to be stable because ρ(t) that determines γg becomes gradually steady from Eq. (8). Simultaneously, the curves show an interesting area where γg is almost equal to zero for Γd ≫ 8 Ω. For the sake of simplicity, we call this area as the near-zero region. In this region, the larger Γd is, the wider the range of the near-zero region is. This is because that the stronger coupling between the DQD system and the QPC causes the electron to be localized in a quantum dot for a long time, which is related to the quantum Zeno effect.[40] As a consequence, the quantum state in the Bloch sphere hardly evolves and the solid angle enclosed by the evolution path is approximately zero after a quasiperiod τ. However, in the case of weaker coupling, such as Γd ≪ 8 Ω, the probabilities of finding the electron in the left or right quantum dot exhibit significant damped oscillations with the increase of Ω and the change of the trajectory becomes large. Then the geometric phase is not zero. Therefore, as we use the QPC to detect the geometric phase of the DQD system, it is necessary to consider its influence on the geometric phase and avoid the near-zero region in order to obtain the desired geometric phase in constructing a quantum logic gate.[39,79,80]

Fig. 2. Geometric phase γg of the DQD system versus the coupling strength Ω between the two quantum dots in the quasiperiod τ with the fixed dephasing rate Γϕ = 0.1 ε for different decoherence rate Γd.

In order to better understand the relation between the geometric phase γg and the coupling strength Ω, we show the evolution path of the open system in the Bloch sphere representation for different Ω in Fig. 3. As Ω increases, the width of the tunneling channel connecting the two quantum dots is expanded, which accelerates the oscillations of the electron between the two quantum dots. Meanwhile, the spiral radius and the length of the path in the Bloch sphere become large with increasing Ω, showing an augment of γg. This means that the expansion of the width of the tunneling channel connecting the two quantum dots could enhance γg. Besides, the trend of γg with Ω is influenced by Γd, i.e., it is steeper with an increase of Γd. So we may manipulate this change of the geometric phase with the coupling strength by adjusting the intensity of the interaction of the DQD system with the detector in practice.

Fig. 3. Bloch sphere representation of the DQD system in the quasiperiod τ for different coupling strength Ω: Ω = 0.5ε (the dashed curve), Ω = 1.5ε (the solid curve), Ω = 2.5ε (the chain curve). Other parameters are chosen as Γd = 1ε and Γϕ = 0.1ε.

In Fig. 4, the geometric phase γg as a function of the coupling strength Ω for different dephasing rate Γϕ is plotted graphically. The figure shows that the slope of γg with Ω is distinct for different dephasing rate Γϕ. For a small Γϕ, γg is rised rapidly with Ω, whereas if Γϕ is large, such as Γϕ = 5ε, γg is increased slowly. As Γϕ departs from zero, the effect of the pure dephasing environment on the DQD system becomes strong, which causes the damping of the off-diagonal terms of ρ(t) and destroys the oscillations of the electron in the DQD. With the phase damping of the system, the path in the Bloch sphere is short enough to approach a line from its initial point to the final point, resulting in a decay of γg.[74] As pointed out in Refs. [44,67], the open DQD system has no geometric phase as the dephasing rate tends to infinity. To some extent, the geometric phase could reflect the strength of the interaction between the system and the environment.

Fig. 4. Geometric phase γg of the DQD system versus the coupling strength Ω between the two quantum dots in quasiperiod τ with the fixed decoherence rate Γd = 0.01ε for different dephasing rate Γϕ.
3.2. Geometric phase in the dissipative environment

In the subsection, we introduce the dissipative environment into the DQD system coupled to a QPC. In the case of the DQD system and the dissipative environment, the reduced density matrix proceeded by the same rotation operation, , , is given by

In this process, with the relaxation rate Γr indicates that the system relaxes from its initial energy state to the lower energy state by emitting photons or phonons, and ρLR(t) decays with time. Then we include the interaction of the QPC, the reduced density matrix has the following forms:[40]

Figure 5 presents the effect of the coupling strength Ω on the geometric phase γg for various decoherence rate Γd. On the whole, γg is increased with increasing Ω and then tends to be stable until the reduced density matrix ρ(t) is stabilized. Similarly, we can see that γg exhibits an obvious near-zero region as well, which is attributed to the stronger decoherence between the system and the QPC, freezing the electron in the DQD system and making the evolution path shorter. Moreover, its range is also constantly expanded as Γd increases. These phenomena are also reflected in Fig. 2, which indicates fully that whether the system is in a pure dephasing environment or a dissipative environment, it is supposed to consider the influence of the decoherence caused by the QPC on the geometric phase when we use it as a detector to study the geometric phase of the DQD system.

Fig. 5. Geometric phase of the DQD system versus the coupling strength Ω between the two quantum dots in quasiperiod τ with the fixed relaxation rate Γr = 0.1ε for different decoherence rate Γd.

As shown in Fig. 6, we show the evolution path of the open DQD system in the Bloch sphere representation for different coupling strength Ω. Clearly, the larger values of Ω imply a bigger radius of the spiral trajectory and a larger geometric phase after quasiperiod τ.[49] In this situation, an increase of the coupling strength would accelerate the oscillations of the electron between the quantum dots and affect the evolution of the quantum state in the Bloch sphere, which leads to an increase of γg. This implies that enhancing the quantum coherence of the system could acquire the larger geometric phase. Moreover, the increasing relationship of the geometric phase with the coupling strength is different for various decoherence rates. Specifically speaking, it will gradually become steep as the decoherence rate increases. We can note that it is important to choose a proper value of the decoherence rate aroused from the QPC for the purpose of obtaining a robust geometric phase during the measurement.

Fig. 6. Bloch sphere representation of the DQD system in a quasiperiod τ for different coupling strength Ω: Ω = 0.5ε (the dashed curve), Ω = 1.5ε (the solid curve), Ω = 2.5ε (the chain curve). Other parameters are chosen as Γr = 0.1ε and Γd = 1ε.

In Fig. 7, we show the evolution of the geometric phase γg with the coupling strength Ω for different relaxation rate Γr. It can be seen from this figure that the changing trend of γg as a function of Ω is significantly different for various Γr. Explicitly, for a given Ω, γg will be reduced with the augment of Γr, which could induce a strong dissipation and a short relaxation time. As Γr deviates from zero, the relaxation time is decreasing and the system will dissipate energy and phase to the environment in a single direction.[81] When Γr is large, such as Γr = 5ε, the relaxation time would be close to or even less than the quasiperiod τ. Under the circumstances, the energy dissipation and phase loss of the system towards the environment become more and more obvious, so the geometric phase becomes small.[52,54,66,75] Namely, the energy dissipation and the phase damping of the system could decrease the geometric phase. If Γr is a very small value, then the relaxation time is much longer than τ. In this case, the environmental effect can be ignored and thus the geometric phase shows a large value within τ. This behavior of γg against the environmental disturbance can be used to deal with certain types of errors in the geometric quantum information.

Fig. 7. Geometric phase of the DQD system versus the coupling strength Ω between the two quantum dots in the quasiperiod τ with the fixed decoherence rate Γd = 0.01ε for different relaxation rate Γr.
4. Conclusions

We study the geometric phase of an open DQD system coupled with a QPC in the pure dephasing and dissipative environments and focus on analyzing the influences of the detector and the two kinds of environments on it. It is demonstrated that the coupling strength between the two quantum dots has an enhanced impact on the geometric phase. Because the expansion of the width of the tunneling channel connecting the two quantum dots accelerates the oscillations of an electron between the quantum dots and increases the length of the evolution path in the Bloch sphere. Moreover, the geometric phase shows a near-zero region due to the quantum Zeno effect that stronger coupling between the system and the QPC leads to the electron to be frozen in one quantum dot and the solid angle enclosed by the evolution path is close to zero. In the pure dephasing environment, the geometric phase is decreased with the increase of the dephasing rate which originates from the phase damping of the system. In the dissipative environment, it is illustrated that the geometric phase is reduced as the relaxation rate grows which results from both the energy dissipation and phase damping of the system. The results provide a theoretical reference for using the geometric phase to construct quantum logical gates based on quantum dot systems. More researches on the geometric phase in the DQD system can be carried out, such as the relationship between the current and the geometric phase in different environments.

Reference
[1] Berry M V 1984 Proc. R. Soc. 392 45
[2] Aharonov Y Anandan J 1987 Phys. Rev. Lett. 58 1593
[3] Samuel J Bhandari R 1988 Phys. Rev. Lett. 60 2339
[4] Sjöqvist E Pati A K Ekert A Anandan J S Ericsson M Oi D K L Vedral V 2000 Phys. Rev. Lett. 85 2845
[5] Tong D M Sjöqvist E Kwek L C Oh C H 2004 Phys. Rev. Lett. 93 080405
[6] Uhlmann A 1986 Rep. Math. Phys. 24 229
[7] Yi X X Chang J L 2004 Phys. Rev. 70 012108
[8] Tong D M Sjöqvist E Filipp S Kwek L C Oh C H 2005 Phys. Rev. 71 032106
[9] Wu B Liu J Niu Q 2005 Phys. Rev. Lett. 94 140402
[10] Carollo A Fuentes-Guridi I Franca S M Vedral V 2003 Phys. Rev. Lett. 90 160402
[11] Cai X J Zheng Y J 2016 Phys. Rev. 94 042110
[12] Cai X J Zheng Y J 2017 Phys. Rev. 95 052104
[13] Cai X J Zheng Y J 2018 J. Chem. Phys. 149 094107
[14] Cai X J 2019 Entropy 21 1040
[15] Cai X J 2020 Sci. Rep. 10 88
[16] Wang Y M Du G Liang J Q 2012 Chin. Phys. 21 044207
[17] Li Z L Bi J J Liu R Yi X H Fu H Y Sun F Wei M Z Wang C K 2017 Chin. Phys. 26 098508
[18] Chiao R Y Wu Y S 1986 Phys. Rev. Lett. 57 933
[19] Tomita A Chiao R Y 1986 Phys. Rev. Lett. 57 937
[20] Jones J A Vedral V Ekert A Castagnoli G 2000 Nature 403 869
[21] Ekert A Ericsson M Hayden P Inamori H Jones J A Oi D K L Vedral V 2000 J. Mod. Opt. 47 2501
[22] Zanardi P Rasetti M 1999 Phys. Lett. 264 94
[23] Fuentes-Guridi I Girelli F Livine E 2005 Phys. Rev. Lett. 94 020503
[24] Wang X B Keiji M 2001 Phys. Rev. Lett. 87 097901
[25] Huang Y Y Wu Y K Wang F Hou P Y Wang W B Zhang W G Lian W Q Liu Y Q Wang H Y Zhang H Y He L Chang X Y Xu Y Duan L M 2019 Phys. Rev. Lett. 122 010503
[26] Duan L M Cirac J I Zoller P 2001 Science 292 1695
[27] Falci G Fazio R Palma G M Siewert J Vedral V 2000 Nature 407 355
[28] Xie H Li H C Yang R C Lin X Huang Z P 2007 Chin. Phys. 16 3382
[29] Jin X R Zhang Y Q Zhang S Jin D Z 2007 Chin. Phys. 16 1220
[30] Zhang Y Q Jin X R Zhang S 2008 Chin. Phys. B 17 424
[31] Yang R C Li H C Lin X Huang Z P 2008 Chin. Phys. 17 180
[32] Zhang L B Song C Wang H Zheng S B 2018 Chin. Phys. 27 070303
[33] Zhu A D Zhang S Yeon K H Yu S C Um C I 2007 Chin. Phys. B 16 1559
[34] Zhou H Li Z K Wang H Y Chen H W Peng X H Du J F 2016 Chin. Phys. Lett. 33 060301 https://cpl.iphy.ac.cn/Y2016/V33/I06/060301
[35] Loss D DiVincenzo D P 1998 Phys. Rev. 57 120
[36] Burkard G Loss D DiVincenzo D P 1999 Phys. Rev. 59 2070
[37] Zanardi P Rossi F 1999 Phys. Rev. 59 8170
[38] Zanardi P Rossi F 1998 Phys. Rev. Lett. 81 4752
[39] Brum J A Hawrylak P 1997 Superlattice. Microst. 22 431
[40] Gurvitz S A Fedichkin L Mozyrsky D Berman G P 2003 Phys. Rev. Lett. 91 066801
[41] Kang L S Zhang Y H Xu X L Tang X 2017 Phys. Rev. 96 235417
[42] Levinson Y 1997 Europhys. Lett. 39 299
[43] van der Wiel W G De Franceschi S Elzerman J M Fujisawa T Tarucha S Kouwenhoven L P 2002 Rev. Mod. Phys. 75 1
[44] Yi X X Wang L C Wang W 2005 Phys. Rev. 71 044101
[45] Lombardo F C Villar P I 2010 Phys. Rev. 81 022115
[46] Rezakhani A T Zanardi P 2006 Phys. Rev. 73 052117
[47] Luo D W You J Q Lin H Q Wu L A Yu T 2018 Phys. Rev. 98 052117
[48] Sjöqvist E Yi X X Åberg J 2005 Phys. Rev. 72 054101
[49] Villar P I Lombardo F C 2011 Phys. Rev. 83 052121
[50] Cai X J Meng R Zhang Y H Wang L 2019 Europhys. Lett. 125 30007
[51] Dajka J Mierzejewski M Łuczka J 2007 J. Phys. 41 012001
[52] Fujikawa K Hu M G 2009 Phys. Rev. 79 052107
[53] Berger S Pechal M Pugnetti S Abdumalikov A A Steffen L Fedorov A Wallraff A Filipp S 2012 Phys. Rev. 85 220502
[54] Guo W Ma J Yin X Zhong W Wang X 2014 Phys. Rev. 90 062133
[55] Li X Shi Y 2013 Europhys. Lett. 103 20005
[56] De Chiara G Palma G M 2003 Phys. Rev. Lett. 91 090404
[57] Abdel-Khalek S Berrada K El-Sayed M A Abel-Aty M 2013 Chin. Phys. 22 100301
[58] Li Z J Cheng L Wen J J 2010 Chin. Phys. 19 010305
[59] Tian L J Zhu C Q Zhang H B Qin L G 2011 Chin. Phys. 20 040302
[60] Wang L C Yan J Y Yi X X 2010 Chin. Phys. 19 040512
[61] Zhang A P Li F L 2013 Chin. Phys. 22 030308
[62] Jia X Y Li W D Liang J Q 2007 Chin. Phys. 16 2855
[63] Zhong W X Cheng G L Chen A X 2010 Chin. Phys. 19 110310
[64] Yuan Z G Zhang P 2015 Chin. Phys. Lett. 32 060301 https://cpl.iphy.ac.cn/Y2015/V32/I06/0603010
[65] Sun S N Zheng Y J 2019 Phys. Rev. Lett. 123 180403
[66] Chen J J An J H Tong Q J Luo H G Oh C H 2010 Phys. Rev. 81 022120
[67] Yi X X Tong D M Wang L C Kwek L C Oh C H 2006 Phys. Rev. 73 052103
[68] Yuan X Z Zhu K D 2006 Phys. Rev. 74 073309
[69] Liu B Zhang F Y Chen Z H Song H S 2013 Int. J. Theor. Phys. 52 1877
[70] Liu B Zhang F Y Song J Song H S 2015 Sci. Rep. 5 11726
[71] Gurvitz S A Mozyrsky D 2008 Phys. Rev. 77 075325
[72] Gilad T Gurvitz S A 2006 Phys. Rev. Lett. 97 116806
[73] Gurvitz S A Berman G P 2005 Phys. Rev. 72 073303
[74] Yin S Tong D M 2009 Phys. Rev. 79 044303
[75] Yin S Tong D M 2010 J. Phys. 43 305303
[76] Gurvitz S A Prager Y S 1996 Phys. Rev. 53 15932
[77] Xu C Vavilov M G 2013 Phys. Rev. 88 195307
[78] Luo J Y Jiao H J Shen Y Cen G He X L Wang C R 2011 J. Phys. Condens. Mat. 23 145301
[79] Nazir A Spiller T P Munro W J 2002 Phys. Rev. 65 042303
[80] Wang H Zhu K D 2008 Europhys. Lett. 82 60006
[81] Wu S L Huang X L Wang L C Yi X X 2010 Phys. Rev. 82 052111