† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61004101), the Natural Science Foundation Program of Guangxi Province, China (Grant No. 2015GXNSFBB139002), the Graduate Innovation Project of Guilin University of Electronic Technology, China (Grant No. GDYCSZ201472), and the Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology, China.
In this paper, successive lag synchronization (SLS) on a dynamical network with communication delay is investigated. In order to achieve SLS on the dynamical network with communication delay, we design linear feedback control and adaptive control, respectively. By using the Lyapunov function method, we obtain some sufficient conditions for global stability of SLS. To verify these results, some numerical examples are further presented. This work may find potential applications in consensus of multi-agent systems.
As an important branch of network science, synchronization of complex networks has been paid great attention and studied deeply in the past two decades. It is well known that synchronization plays an important role in various fields, such as laser systems, communication systems, and parallel image processing.[1–6] In the research of complex dynamical networks, a variety of synchronization patterns have been defined and studied, including complete synchronization,[7] partial synchronization,[8] cluster synchronization,[9,10] projective synchronization,[11] phase synchronization,[12] lag synchronization (LS),[13] generalized synchronization,[14] etc. Among these patterns, the LS between two coupled systems has been studied extensively.[15–17]
Most existing researches of LS are based on two coupled dynamical systems (or networks). The LS is achieved if y(t) → x(t − τ), τ > 0 as t → + ∞, which is investigated originally in Ref. [13]. From then on, LS has gradually become a research focus. The LS has been generalized to many other forms, including projective lag synchronization,[18] generalized lag synchronization[19] and successive lag synchronization (SLS).[20] Here, SLS, a new kind of lag synchronization in a multi-coupled dynamical system proposed by Li in Ref. [20], can be considered as a generalized pattern of the traditional LS in two coupled systems. SLS means that a node achieves the LS with its next node, i.e., xi(t − τ) → xi+1(t) for a positive time delay τ as t → +∞. It may be found potential applications of SLS in multi-agent systems. For example, in military parade, sometimes we can see that the aircrafts (nodes) pass the same spatial position with the same time delay to avoid collision and keep orderly queue, which can be considered as the SLS realization of these aircrafts. In Ref. [20], the authors supposed that there is no communication delay between nodes in the network means that each node in the network can immediately receive the coupling signals from its neighbor nodes. However, because of the finiteness of signal transmission and switching speed, the communication delay is inevitable in real dynamical systems.[21] Communication delay often appears in numerous systems frequently, such as aircraft, seismology, and laser systems.
Motivated by the above discussions, the main aim of this paper is to construct a general dynamical network with communication delay and investigate its SLS. Based on the constructed dynamical network, we apply linear feedback control and adaptive control to achieve its SLS. Depending on topological structure of the considered dynamical network, a linear feedback control is designed to realize its SLS. Moreover, in order to choose the feasible control adaptively, an adaptive linear feedback control is also proposed. By using the Lyapunov function method and Barbalat’s Lemma, some sufficient conditions for the global stability of SLS are obtained.
The rest of this paper is organized as follows. In Section 2, we give some Lemmas and some preliminaries about the model formulation of a dynamical network with communication delay. In Section 3, we investigate the global stability conditions of the SLS of the dynamical network under linear feedback control and adaptive linear feedback control, respectively. In Section 4, some numerical examples are performed to verify the theoretical results. Finally, in Section 5, we conclude the paper.
The considered dynamical network with communication delay under control is described as follows:
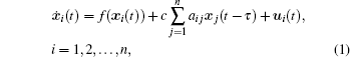
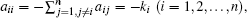
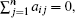
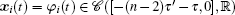
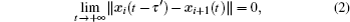
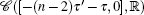
It should be noticed that we should first number the nodes in a network according to the Definition 1 to prepare for the study of its certain SLS. The schematic figure of SLS is shown in Fig.
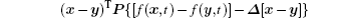
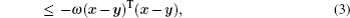

From Barbalat’s Lemma, Li gives the following result in Ref. [20].
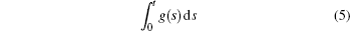
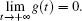
In order to eliminate suppressive items in the following error system (10) and accelerate the realization of SLS, we design the following preliminary functions and control. First, for i = 1,2,…,n − 1, some preliminary functions are defined as

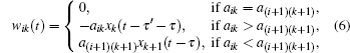

Then a linear feedback control can be designed as
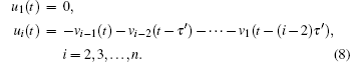

According to Definition 1, the SLS errors of dynamical network (
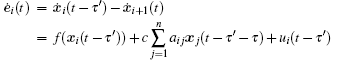
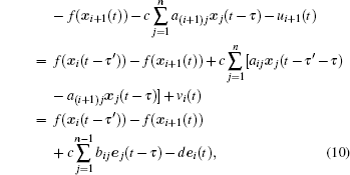

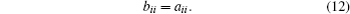
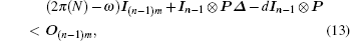
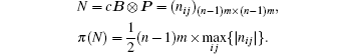
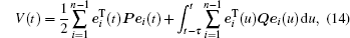
The derivative of V(t) along the trajectories of error system (
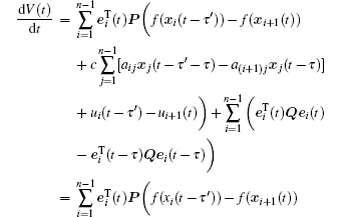
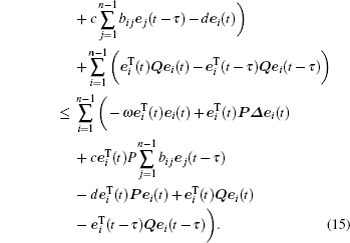
Letting 

From condition (
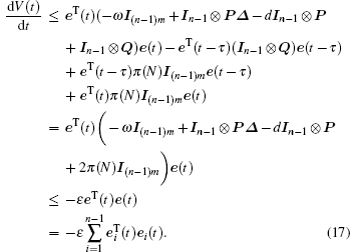
Integrating the above equation from 0 to t yields
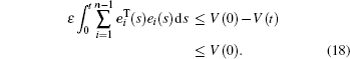
Thus, the integral 
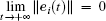
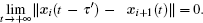
In practice, the control strength is not allowed to be arbitrarily large, so we adopt an adaptive control method[22] to reduce the control strength.
For i = 1,2,…,n − 1, some preliminary functions are similarly defined as

Then an adaptive control is designed as
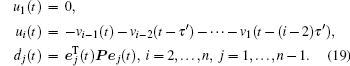
Suppose that

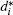
The derivative of V(t) along trajectories of error system (
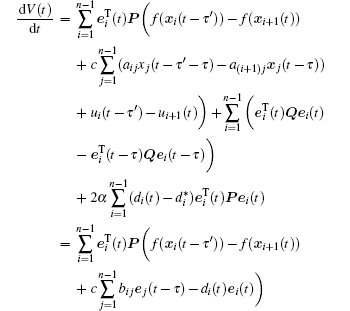
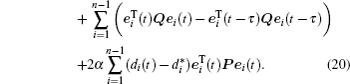
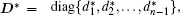
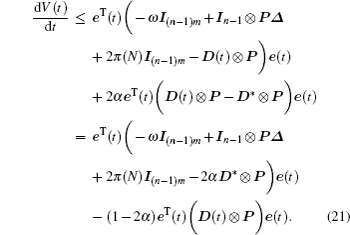
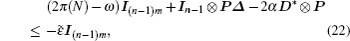
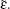
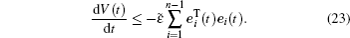
Thus, the integral 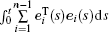

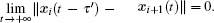
In this section, some numerical examples are given to verify the theorems in Section 3. The size of dynamical network (
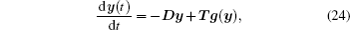
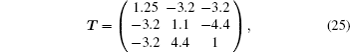
 | Fig. 2. Two kinds of topological structure for dynamical network ( |
First, we use linear feedback control (


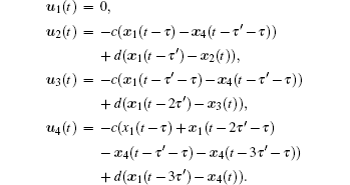
We can obtain π(N) = (n − 1)m × maxij{|nij|}/2 = 9c from the matrix
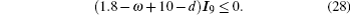
We can easily get the lower bound of the control strength dl = 11.18. So, if d > dl, the conditions of Theorem 1 are satisfied, which means that the SLS of dynamical network (
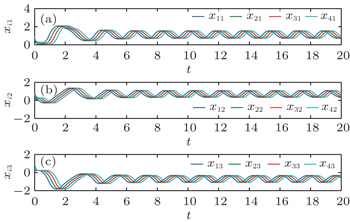 | Fig. 3. Trajectories of (a) xi1, (b) xi2, and (c) xi3 of dynamical network ( |
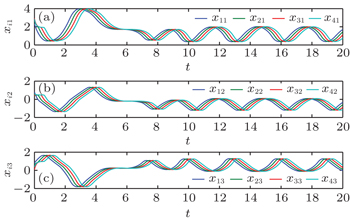 | Fig. 4. Trajectories of (a) xi1, (b) xi2, and (c) xi3 of dynamical network ( |
Now, we use adaptive control (
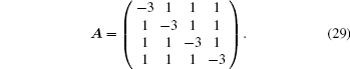

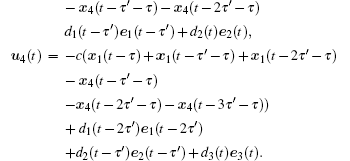
Figure
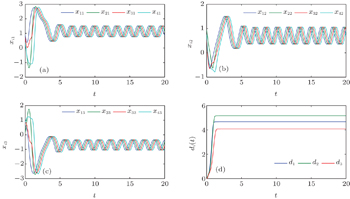 | Fig. 6. Trajectories of all state variables (a) xi1, (b) xi2, (c) xi3, and (d) di(t) of dynamical network ( |
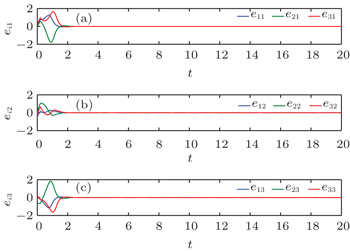 | Fig. 7. Trajectories of all SLS errors (a) ei1, (b) ei2, and (c) ei3 of dynamical network ( |
Similar to that in subsection 4.1, by solving the following inequality:
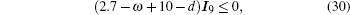
In this paper, we address the successive lag synchronization (SLS) on dynamical networks with communication delay via linear feedback control and adaptive linear feedback control. We construct a general dynamical network with communication delay to make the SLS more realistic and significant for real multi-coupled systems. By using the linear feedback control, the SLS of the network has been realized. In order to choose the feasible control gain adaptively, we design an adaptive linear feedback control. By theoretical analysis, we obtained some sufficient conditions for the global stability of SLS under the controls.
In many real dynamical networks, their topological structures may be generally directed. Therefore, it is worth to consider SLS of dynamical networks with directed topological structures in the future.





