†Corresponding author. E-mail: hengfulin@126.com
*Project supported by the National Key Basic Research Special Foundation of China (Grants Nos. 2011CB921502 and 2012CB821305), the National Natural Science Foundation of China (Grants Nos. 61227902, 61378017, and 11434015), the State Key Laboratory for Quantum Optics and Quantum Optical Devices, China (Grant No. KF201403).
Magnetic adatoms in the honeycomb lattice have received tremendous attention due to the interplay between Ruderman–Kittel–Kasuya–Yosida interaction and Kondo coupling leading to very rich physics. Here we study the competition between the antiferromagnetism and Kondo screening of local moments by the conduction electrons on the honeycomb lattice using the determinant quantum Monte Carlo method. While changing the interband hybridization V, we systematically investigate the antiferromagnetic-order state and the Kondo singlet state transition, which is characterized by the behavior of the local moment, antiferromagnetic structure factor, and the short range spin-spin correlation. The evolution of the single particle spectrum are also calculated as a function of hybridization V, we find that the system presents a small gap in the antiferromagnetic-order region and a large gap in the Kondo singlet region in the Fermi level. We also find that the localized and itinerant electrons coupling leads to the midgap states in the conduction band in the Fermi level at very small V. Moreover, the formation of antiferromagnetic order and Kondo singlet are studied as on-site interaction U or temperature T increasing, we have derived the phase diagrams at on-site interaction U (or temperature T) and hybridization V plane.
The strongly correlated systems containing both itinerant electrons and local moments continue to attract intensive interest in modern condensed matter physics, since they exhibit fascinating behaviors, such as the heavy quasi-particle formation in the heavy electron compounds that contain rare earth elements, [1] the unconventional superconductivity[2] firstly observed in UBe13, [3] and non-Fermi liquid behavior.[4, 5] To understand those novel phenomena, we should consider two competing interactions, the direct Kondo coupling and the indirect Ruderman– Kittel– Kasuya– Yosida (RKKY) interaction. The former promotes singlet formation between conduction and localized electrons, whereas the latter favors magnetic ordering. The competition also leads to a quantum critical point between spin-singlet states and a magnetically ordered state, which is the source of non-Fermi-liquid behavior and superconductivity. Theoretically, the Kondo lattice model is the most celebrated starting point for the investigation of the interplay between localized spins and itinerant electrons. It provides the canonical explanation for the Kondo effect and the heavy-fermion effect in many materials.[6– 8] The physics of the Kondo lattice model on nonfrustrated lattice, [9, 10] such as the square lattice and cubic ones, has been studied extensively.
Many-body system problems in the honeycomb lattice system have been extensively studied, such as the correlated electrons in the graphene[11– 14] and silicene, [15– 17] where a number of exotic phenomena are found theoretically and experimentally. Although the honeycomb lattice is also bipartite, it has the smallest possible coordination number for proper two-dimensional lattices. As a result, the honeycomb lattice can support physical phenomena fundamentally different from square lattices illustrated by recent numerical calculations and analytical studies, such as the novel spin-liquid phase or quantum criticality for Hubbard model, [18, 19] the topological Mott insulator for the extended Hubbard model.[20, 21] Recently, coupling of conduction electrons to local magnetic moments has been realized in graphene, and the Kondo effect has been observed with point defect.[22] The formation of a Kondo screening cloud around a magnetic adatom drives the system from a semimetal with vanishing density of state in the Fermi level to the standard Fermi liquid with density of states restored by disorder.[23– 25] However, the conduction electrons interplay with the densely localized spins on the honeycomb lattice, which could be encoded in terms of the Kondo lattice model, is a largely open problem.
From the perspective of heavy fermion physics, there are many materials, in which the essence of the electronic structure is capture by interacting spins and electrons on a honeycomb lattice. Firstly, such system is relevant for the impurity magnetic moments on honeycomb lattice of graphene, which could be fabricated by the molecular beam epitaxy technique. This has been intensively studied theoretically in a Ruderman– Kittel– Kasuya– Yosida framework[26] using the Kondo lattice model.[27] Secondly, the system could be realized in transition metal oxides, e.g., Bi3Mn4O12(NO3)[28, 29] or Li2MnO3, with Mn ions[30] on a honeycomb lattice. Finally, since the Kondo– correlated state was realized using the ultracold atom, [31] recently, such a system could be realized by loading the cold atoms in the optical lattice.[32– 34]
In this paper, we will obtain a systematical picture of the nature of the antiferromagnetism-Kondo singlet competition and related aspects of Kondo physics with itinerant fermions and local moments in the honeycomb lattice at finite temperature. Using the determinant quantum Mente Carlo method (QMC), we investigate the periodic Anderson model, which is a parent model for Kondo lattice model capturing the main physics in this system. Firstly, in order to study the magnetic correlation of the system, we calculate the follow qualities, local moments, the antiferromagnetic structure factor, and the short-range spin– spin correlation. We find that the system shows a phase transition from antiferromagnetic-order phase to Kondo singlet phase as increasing the interband hybridization V for fixed on-site interaction U. Then, we systematically investigate the spectral properties of the system, including the local density of state, k-resolved spectral density. In the small V region, the spectrum of excitations shows a resonance peak at high temperature and a well-developed gap associated with the long-range antiferromagnetic order at low temperature in the Fermi level. In the large V region, there is a large Kondo insulator gap for all the temperatures. At last, we present the comprehensive phase diagrams in the U– V plane and the T– V plane.
The remainder of this paper is organized as follows. In Section 2, we introduce the Hamiltonian of two effective models in the honeycomb lattice: Kondo lattice model and periodic Anderson model, to describe the system containing itinerant electrons and local moments, and briefly summarize the determinant quantum Monte Carlo method employed. Section 3 presents the main results of our QMC studies, including the magnetic correlations, spectral properties, and phase diagrams. The conclusion is presented in Section 4.
One of the popular models to describe the physics of the system containing the itinerant electrons and localized spin moments is the Kondo lattice model. Here, we consider the Kondo lattice model defined on the honeycomb lattice at half-filling (see Fig. 1(a)), and the effective Hamiltonian is given by
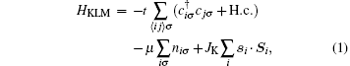
where 

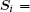


This model is relevant for the understanding of heavy electron materials. The nature of the ground state results from the competition of the Kondo coupling and the Ruderman– Kittel– Kasuya– Yosida interaction. The polarization cloud of conduction electrons produced by a local moment may be felt by another local moment. This provides the mechanism for the Ruderman– Kittel– Kasuya– Yosida interaction between localized moments, which tend to stabilize a magnetic order.[35] On the other hand, the same polarization cloud may form a singlet bound state with the local moment, [36] as the so-called Kondo effect. Comparing energy scales, the RKKY interaction dominates at small J and the Kondo effect dominates at large J. In a non-frustrated square lattice, a quantum transition between magnetically ordered and disordered phases is shown using the quantum Monte Carlo method.[19] In geometrical frustrated lattice, more exotic phenomena and novel phases are emergent in this model, partial Kondo screening, [37] charge order phase, [38] and partial disorder phase.[39]
In the honeycomb lattice, the itinerant electrons in the conduction c-band are described by massless Dirac fermions at low energies in the tight-binding limit J = 0 (see Figs. 1(c) and 1(d)). In this system, since the density of states is low in the Fermi level, the interaction effect can be suppressed.[11] It is no wonder that the competition between the Kondo coupling and the Ruderman– Kittel– Kasuya– Yosida interaction will show very different behaviors. To proceed, we map Kondo lattice model onto the periodic Anderson model (see Fig. 1(b)), [40, 41] which is also one of the most popular model to describe the physics of heavy fermion materials. The Hamiltonian is given by




where Hc is the tight-binding Hamiltonian, Hcf is the hybridization between the itinerant c-electrons and localized f-electrons, and Hf is for the local electrons with ε f being the local energy level and U the on-site Coulomb repulsion of local electrons.
The two models are equivalent provided that the f electrons are in the Kondo regime. In the large U/V limit, the charge fluctuations become effectively frozen and the ground state wave function has little weight of configurations with the number of f electrons different from its average number 

where ε F is the Fermi energy of the conduction band.
Solutions of both models in a general case represent a complicated analytical and numerical problem. In this paper, we concentrate on the periodic Anderson model. To capture the relevant physics we employ the determinant quantum Monte Carlo method.[42– 44] At small and large hybridization V, the system is adiabatically connected to, respectively, the V = 0 and V = ∞ limits. The system is made up of a magnetical-order layer weakly coupled to semi metal (or Dirac fermion). Here we are interested in semi-metallic heavy fermions, and restrict ourselves to study the system at half-filling. Besides, the QMC method is free of the notorious sign problem at half-band filling.
Within the determinant quantum Monte Carlo method, the partition function is expressed as a path integral by using the Suzuki– Trotter decomposition of exp(− β H), where β = 1/kBT with kB the Boltzmann constant. After discretization the imaginary time, the partition function is written as a product of incremental imaginary time propagators exp(− Δ τ H), the Trotter steps are taken to be Δ τ = β /M and M ranges from 20 to 200 depending on the temperature and the on-site interaction. We have checked that the simulation results converge with varying the values of Δ τ . The interaction term is decoupled through a discrete Hubbard– Stratonovich transformation, which introduces an auxiliary Ising field. Instead of using the Hubbard– Stratonish transformation in the spin channel, we adopt the Hubbard– Stratonish transformation in the charge channel which maintains the SU(2) symmetry explicitly.
We present our QMC simulations of thermodynamic quantities of the periodic Anderson model on a L × L honeycomb lattice with the periodical boundary condition. The results we present are mostly computed for lattices of N = 6 × 6 × 2 sites, and two bands. For some qualities, we have carried out the finite size scaling analysis. The QMC algorithm has been refined by including “ global moves” to improve ergodicity[45] and “ delay updating” of the fermion Green’ s function, which increases the efficiency of the linear algebra. This method gives rise to errors on the order of (Δ τ )4.
In the period Anderson model, the on-site repulsion U in the f -band favors localization of electrons, resulting in the local moments, by impeding the double occupancy. To gain initial quantitative understanding of the evolution of magnetic properties as hybridization V increases, we calculate the local moments in the c-band and the f -band. The local moments are defined as
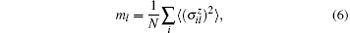
where l ∈ c or f -band, 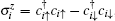

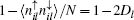
As hybridization V increases, the local moments gradually disappear in f band. For small hybridization V, the f electrons in the local band and c electrons in the conduction band are completely decoupled. It is no wonder that the local moment approaches 1 in the local band, the two singly occupy | ↑ ⟩ and | ↓ ⟩ are allowed, while the empty | 0⟩ and doubly occupied ones | ↑ ↓ ⟩ are forbidden. The local moment in the conduction band approaches 0.5, each of the four possible sites occupy is equally. In the large hybridization V limit, the c and f electrons form Kondo singlets, the local moments become small and almost the same in the two bands. The temperature dependence of the localized moment in each band is also shown in Fig. 2. When the temperature (T = 1/5, 1/10) is high, it has little influence on the local moments. However, when the temperature (T = 1/20) is below the coherent energy scale, the local moments will suddenly become larger, especially for c band and large V limits.
It is well known that when the conduction band is a normal metal, the period Anderson model in the square lattice, there is a competition between the RKKY interaction and the Kondo effect. For small values of V, the RKKY interaction favors ordering the mangnetic moments of the localized f electrons, while the Kondo effect screens the localized magnetic moments due to the formation of spin singlets between the two bands. In order to determine the antiferromagnetically ordered from the disordered phase, we calculate the antiferromagnetic structure factor 
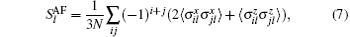
where 


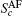

Then we use finite size scaling on 
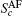


Besides the local moment and antiferromagnetic structure factor, the short-range spin– spin correlations are important quantities for describing the magnetic fluctuation in a system. Here, we consider three spin correlations, the nearest neighbor spin– spin correlation ⟨ si · si+ 1⟩ on the conduction c-band, the nearest neighbor spin– spin correlation ⟨ Si · Si + 1⟩ on the localized f -band, and the on-site correlation ⟨ si · Si⟩ between the conduction band and localized band. Figure 4 shows the three correlations as a function of hybridization V for various values of temperature at U = 4.0 (left panels) and U = 8.0 (right panels).
In the small V case, the ⟨ si · sj+ 1⟩ on the conduction c-band has a very large value, although the conduction band does not have a long-range order in this region. With the increase of the hybridization V, the ⟨ si · si+ 1⟩ gradually disappears, the temperature has no significant effect on this behavior, as shown in Figs. 4(a1) and 4(b1). However, the behavior of the ⟨ si · Si⟩ is different, we can see that the ⟨ si · Si⟩ increases as the increase of the hybridization V as shown in Figs. 4(a3) and 4(b3). The ⟨ si · Si⟩ increases to a large nonzero value for large V, where the Kondo singlet is formed. The ⟨ si · Si⟩ can be viewed as a parameter for the Kondo singlet formation. The evolution behaviors of ⟨ Si · Si+ 1⟩ are shown in Figs. 4(a2) and 4(b2), it will firstly increase to a large value, and then decrease when V increases gradually. As the temperature is lowered, the ⟨ Si · Si+ 1⟩ will be enhanced, which is similar to the long-range order antiferromagnetic structure 
Now, we discuss the phase changes from the viewpoint of the electronic state. When the hybridization V = 0, the properties of the periodic Anderson model are simple, the individual local moments completely decouple from the conduction band. However, in the nonzero V case, the f electrons and itinerant c electrons change their characters depending on each other. From the well studied case, the period Anderson model in the square lattice in which the local electrons are coupled to the normal metal, we learn that the localized f electrons tend to form magnetically ordered states with intersite exchange interactions, while the acquired itinerancy by the Kondo effect results in a heavy Fermi liquid. Intriguing phenomena such as quantum criticality and unconventional ordered states have been observed in the competing region. Besides, the difference between the itinerant and localized characters appears in the Fermi surface, itinerant f electrons contribute to the Fermi volume, while the localized one does not. The spectrum of excitations of the period Anderson model in the square lattice displays complex features, which can reflect the interplay of antiferromagnetic order, the formation of a Mott insulator, and the emergence of Kondo singlets. In the honeycomb lattice, in the half-filling case, the electrons in the conduction band are described by massless Dirac fermion with linear low energy dispersion relation E(k) = ± ν F| k| , and the density of states vanishes at the Fermi level. This fact implies that the spectrum of excitations of the periodic Anderson model in honeycomb lattice has different behaviors, due to the low density of states at Fermi level in the conduction band.
The single particle spectral density of the c-band ρ c(ω ) and the f -band ρ f (ω ) are plotted in Fig. 5. We extract the single particle excitation spectra ρ l(ω ) via analytic continuation of the local time-dependent Green function 


In Fig. 5, we show the density of states in the c-band (Figs. 5(a1)– 5(d1)) and f -band (Figs. 5(a2)– 5(d2)) as a function of the interband hybridization V at temperatures T = 1/5 and T = 1/20 for two values of on-site interaction U = 4.0 and 8.0. The temperature T and on-site U have no significant effect on the spectrum of excitations (see Fig. 5), due to the biparticle nature of the honeycomb lattice and the linear band crossing point in the Fermi level. However, with the varying of the hybridization strength V, the spectrum of excitations changes very much. At very small hybridization V, (V = 0.2 at T = 1/5, 1/20.0 and U = 4.0, 8.0) the system can be seen as that the individual moments are completely decoupled from the conduction band. In the local f electrons have two dispersiveless Hubbard band (see Figs. 5(a2)– 5(d2)). We also find that the small hybridization of the itinerant electrons and localized electrons change the lower energy properties of the electrons in the conduction band, resulting in finite density of state in the Fermi level. As the temperature is lowered from T = 1/5 to T = 20, there is a quasiparticle peak in the Fermi level (see Figs. 5(a1)– 5(d1)), the itinerant electrons show the Fermi liquid behavior at low temperature.
In the intermediate V side (V = 1.0 at T = 1/5, 1/20 and U = 4.0, 8.0), the RKKY interaction is dominant, and the system shows a long-range antiferromagnetic order at the low temperature. In this region, at higher temperature T = 1/5 there is a resonance peak at Fermi level in both conduction band and local band (see Figs. 5(a1), 5(a2), 5(c1), and 5(c2)), due to the screen of the local moments by the conduction electrons. However, at the lower temperature T = 1/20 the resonace peak is suppressed, a well-developed gap is formed. The gap is associated with the long-range antiferromagnetic order. In the large V side, (V = 2.0, 4.0 at T = 1/5, 1/20 and U = 4.0, 8.0), the system goes to the Kondo singlet phase, we do not find any resonance peak in the Fermi level at high temperature 1/5, both the conduction and local band have a large Kondo insulator gap in the Fermi level at all temperatures. The gap grows with the increase in hybridization V for any fixed on-site interaction U.
It is interesting that in the small V side, there are finite densities of states in the Fermi level in the conduction band (see Figs. 5(a1)– 5(d1)). That means that the localized and itinerant electrons coupling can lead in gap state in the conducting bands in the Fermi level. Such things that have been studied based on the Dirac equation lead to localized states in samples with edges[47] or lattice defects, [48] these states change the densities of states near the Dirac energy, as they induce a peak at this energy.
To see the difference between the antiferromagnetic-order state at small V side and Kondo insulator at large V side more clearly, we now study the dispersion relation of those two states. The quantity is defined as
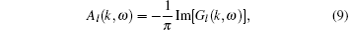
where l = c and f. In Fig. 6, we plot the k-resolved spectral density Ac(k, ω ) in the c band and Af (k, ω ) in the f band. We intentionally consider points far from the phase transition point to show that results are robust and do not depend on the vicinity to special points in the phase diagram. The system is the antiferromangeitc phase for V = 1.0 (see Figs. 6(a1) and 6(a2)). The Ac(k, ω ) is close to the noninteracting honeycomb lattice, with a small gap opening in the Fermi level in the K points. The Af (k, ω ) gives two resonance bands around the Fermi level, and there is a small gap between those two bands. The system is the Kondo insulator phase for V = 4.0 (see Figs. 6(b1) and 6(b2)). Both the Ac(k, ω ) and the Af (k, ω ) have a large gap in the Fermi level, with two nondispersing bands. The striking difference with respect to the antiferromagnetic-order phase is the big rearrangement of the spectral weight, due to the Kondo screen effect of itinerant electrons and localized electrons. In experiment, the changes of the spectrum can be detected according to the behavior of the Hall coefficient[54] and the de Haas-va Alphen frequencies.[55]
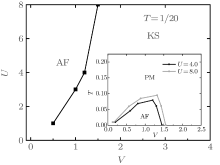
From the systematical study of the magnetic and spectral properties in the periodic Anderson model, we have gained the main physics due to the competition of the itinerant and localized electrons in the honeycomb lattice. We perform similar calculations for various values of on-site interaction U, hybridization V, and temperature T. Based on the magnetic properties as well as the spectral properties, we obtain the phase diagram of the period Anderson model in the honeycomb lattice. In Fig. 7, we show the U– V phase diagram for temperature T = 1/20 obtained in this manner. The antiferromagnetic order to Kondo singlet phase transitions occur at V ∼ 1.2 for U = 4.0, and V ∼ 1.5 for U = 8.0. For small V, the system shows antiferromagnetic order, in which the staggered antiferromagnetic structure factor 

Finally, let us discuss finite temperature properties of the system, and obtain the finite temperature phase diagram. The inset of the Fig. 7 exhibits the phase diagram for U = 4.0 and U = 8.0 on the plane of the temperature T and hybridization V. The result shows that the model exhibits antiferromagnetic order in the small coupling regions V < 1.2 for U = 4.0 and V < 1.5 for U = 8.0 for temperature T = 1/20. As shown in the inset of Fig. 7, the critical temperature TAF grows as increasing V, whereas it suddenly disappears for V larger than a critical values in the T ranged calculated. The the critical temperature TAF of the antiferromagnetic-order phase at U = 4.0 is smaller than that at U = 8.0 for the same values of hybridization V, which shows that the increase of the on-site interaction U will enlarge the region of antiferromagnetic-order phase in the finite temperature.
In this paper, we study the competition between the Ruderman– Kittel– Kasuya– Yosida interaction mediated by the itinerant electrons and their Kondo coupling with local moments densely distributed on the honeycomb lattice using the determinant quantum Monte Carlo method, based on the periodic Anderson model at half filling at finite temperature. We systematically investigate behaviors of the local moments, antiferromagnetic structure factor, and short-range spin– spin correlation in both the conduction c-band and localized f -band. We find that the long-range antiferromagnetic order only survives in the localized f -band for small hybridization V, and quantitatively determine the phase transition between the antiferromagnetic-order phase and Kondo singlet phase as varying the V. We also analyze the electronic properties of the system both in the conduction c-band and localized f -band. The spectrum of excitations has a striking change from the antiferromagnetic-order phase to Kondo singlet phase. Besides, we find that the localized and itinerant electrons coupling lead to the in-gap state in the conduction band in the Fermi level for very small V.
Moreover, by changing the on-site interaction U and temperature T, we give a more detail discussion of the magnetic properties and spectral properties and present the phase diagrams at the U– V plane and the T– V plane. With the increase of the on-site interaction U, the phase transition point V* of the antiferromagnetic-order phase to Kondo singlet phase will increase. The region of the antiferromagnetic-order phase in the finite temperature phase diagram is enlarged when the on-site interaction U increases.
Our study provides an important step for understanding the quantum phase transition of the honeycomb lattice with both itinerant electrons and local moments. To confirm the findings in our work, other complementary analytical or numerical methods can be used, such as dynamical mean field theory[49] or cluster extension of the DMFT.[50, 51] At last, it is expected that the system could be realized by experiments of ultra-cold atoms on the honeycomb optical lattices. The magnetic correlations and quasiparticle spectral can be probed by neutron scattering, nuclear magnetic resonance (NMR), [52] the angle-resolved photoemission spectroscopy (ARPES), [53] the Hall effect, [54] and de Hass-Va Alphen frequency measures.[55]
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|