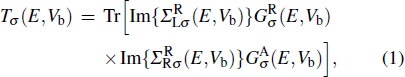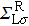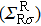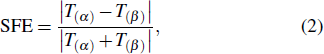Cite this Article
Zeng Jing, Chen Ke-Qiu, Zhou Yanhong. Exploring how hydrogen at gold–sulfur interface affects spin transport in single-molecule junction. Chinese Physics B, 2020, 29(8): 088503  
Permissions
Exploring how hydrogen at gold–sulfur interface affects spin transport in single-molecule junction
Zeng Jing1, 3, †, Chen Ke-Qiu2, ‡, Zhou Yanhong4
College of Physics and Electronic Engineering, Hengyang Normal University, Hengyang 421002, China
Department of Applied Physics, School of Physics and Electronics, Hunan University, Changsha 410082, China
Hunan Provincial Key Laboratory of Intelligent Information Processing and Application, Hengyang 421002, China
College of Science, East China Jiao Tong University, Nanchang 330013, China

 

† Corresponding author. E-mail: zengjing@hynu.edu.cn keqiuchen@hnu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11674092, 11804093, and 61764005), the Natural Science Foundation of Hunan Province, China (Grant No. 2019JJ40006), the Scientific Research Fund of the Education Department of Hunan Province, China (Grant No. 18B368), the Science and Technology Development Plan Project of Hengyang City, China (Grant No. 2018KJ121), and the Science and Technology Plan Project of Hunan Province, China (Grant No. 2016TP1020).

Abstract

Very recently, experimental evidence showed that the hydrogen is retained in dithiol-terminated single-molecule junction under the widely adopted preparation conditions, which is in contrast to the accepted view [Nat. Chem. 11 351 (2019)]. However, the hydrogen is generally assumed to be lost in the previous physical models of single-molecule junctions. Whether the retention of the hydrogen at the gold—sulfur interface exerts a significant effect on the theoretical prediction of spin transport properties is an open question. Therefore, here in this paper we carry out a comparative study of spin transport in M-tetraphenylporphyrin-based (M = V, Cr, Mn, Fe, and Co; M-TPP) single-molecule junction through Au–SR and Au–S(H)R bondings. The results show that the hydrogen at the gold–sulfur interface may dramatically affect the spin-filtering efficiency of M-TPP-based single-molecule junction, depending on the type of transition metal ions embedded into porphyrin ring. Moreover, we find that for the Co-TPP-based molecular junction, the hydrogen at the gold–sulfur interface has no obvious effect on transmission at the Fermi level, but it has a significant effect on the spin-dependent transmission dip induced by the quantum interference on the occupied side. Thus the fate of hydrogen should be concerned in the physical model according to the actual preparation condition, which is important for our fundamental understanding of spin transport in the single-molecule junctions. Our work also provides guidance in how to experimentally identify the nature of gold–sulfur interface in the single-molecule junction with spin-polarized transport.

PACS: ;85.65.+h;;73.40.-c;;73.63.-b;
Keyword:;transport properties;;molecular electronic devices;;gold-sulfur interface;;density-functional theory;;nonequilibrium Green’s functions;
1. Introduction

Silicon-based electronic devices will face insurmountable challenges when they approach to the nano-size.[1] Recently, building single-molecule devices has become possible due to the progress of microfabrication and self-assembly techniques.[2] Electronic devices comprised of single molecules have been considered as a promising solution to achieving the miniaturized electronic circuits. So far, great efforts have been made to build molecular systems with various functionalities, including switching,[3–6] rectification effect,[7,8] long-range charge transport,[9] thermoelectric energy conversion,[10,11] spin-filtering effect,[12] magnetoresistance effect,[13,14] etc.

The thiol linkers are often used to build molecular junctions where molecular backbones are coupled to two gold electrodes.[7,9,12,15–28] The fate of hydrogen is a controversial topic in the experiments when thiols are connected to gold surfaces.[29] The accepted view is that the hydrogen is lost when the gold–sulfur interface is formed. Following the experimental studies, the hydrogen is generally assumed to be lost when the theoretical models of single-molecule junctions are constructed. However, Inkpen et al.[30] found that the gold–sulfur interface in self-assembled monolayers prepared from the solution deposition of dithiols displays a non-chemisorbed interaction, and the hydrogen attached to the sulfur still exists, which is inconsistent with the accepted view. As this preparation method adopted by Inkpen et al. is widely used to construct single-molecule junctions, the effect of the hydrogen attached to the sulfur on physical properties should be concerned when we explore the corresponding theoretical models. On the other hand, how to effectively identify the nature of gold–sulfur interface of the molecular spintronic device in experiment has not been explored yet. Therefore, in the present work, single-molecule junctions consisting of gold electrodes bridged by M-tetraphenylporphyrin (M = V, Cr, Mn, Fe, and Co; M-TPP) via Au–SR/Au–S(H)R bonding are investigated through spin-transport calculations.

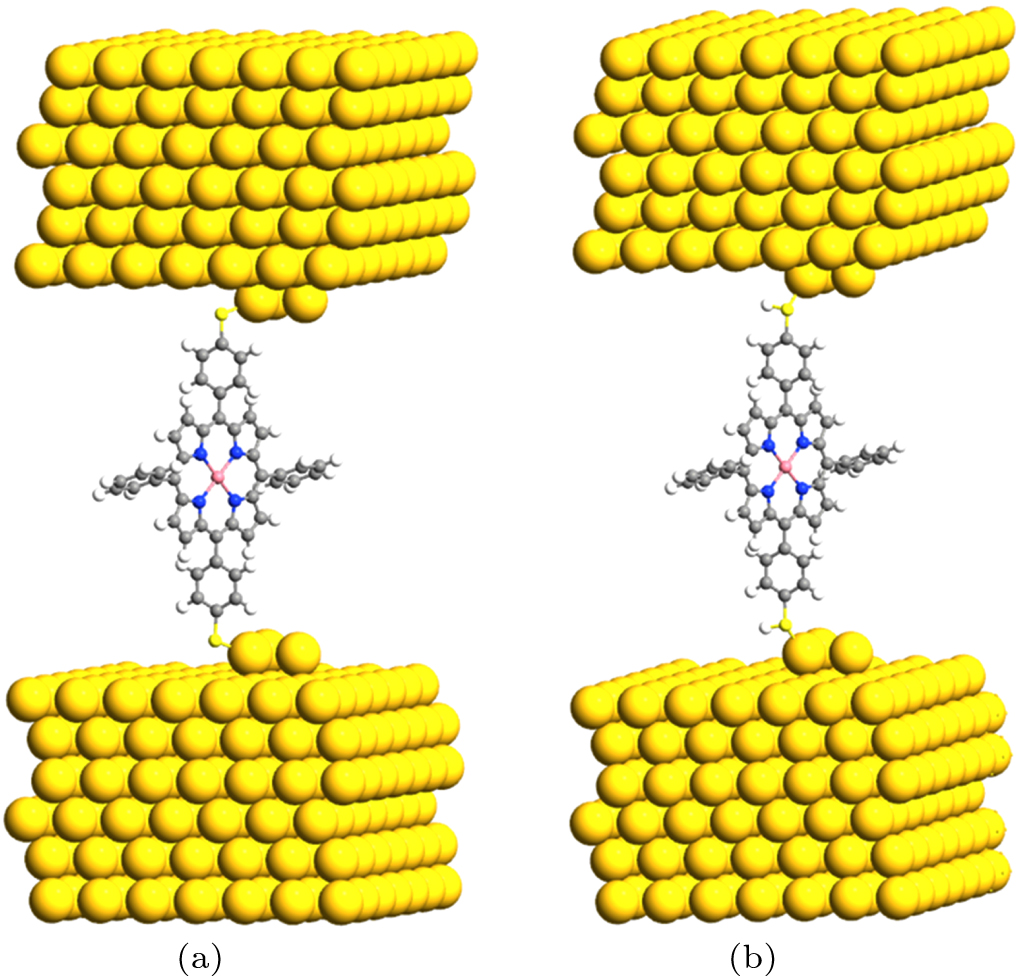
2. Method and model

The molecular junctions under our investigation are displayed in Fig. 1. In the central region of the junctions, a single TPP is connected to the extended Au(111)-(7 × 7) electrodes through Au–SR [see Fig. 1(a)] and Au–S(H)R [see Fig. 1(b)] bonding. Following the previous report,[30] the Au triad junction structure is used to model experimental transport measurements. Kuang et al.[9] have shown that the TPP can be converted into transition-metal-doped TPP by using on-surface metalation. Thus, we investigate the spin-polarized transport properties of the TPP embedded with first-row transition metals in which there exist a different number of electrons. The lengths of gold–sulfur bonds in the Au–SR bonding case are in a range of about 2.381 Å–2.386 Å and in the Au–S(H)R bonding case they are in a range of 2.569 Å–2.582 Å. For convenience, the models in Figs. 1(a) and 1(b) are termed M-TPP(S)2 and M-TPP(SH)2, respectively.

Fig. 1. Geometrical models showing M-TPP-based molecular junctions through Au–SR and Au–S(h)R bondings.

The spin transport calculations are performed by using the ATOMISTIX TOOLKIT package, in which adopted is the nonequilibrium Green’s function (NEGF) in combination with density functional theory (DFT).[31] In the transport calculation, the DFT with the Perdew–Burke–Ernzerhof exchange–correlation functional, double-ξ polarized basis set for the TPP and S atoms, and single-ξ (SZ) basis set for the gold electrodes, are adopted. For the gold electrodes, the SZ basis set is extensively tested in the transport calculation of single-molecule junction, and it is found that a balance between the computational demands and accuracy can be realized.[19,20] The cutoff energy, the k-point sampling, and the electron temperature are set to be 150 Ry (1 Ry = 13.6056923(12) eV), 3× 3× 100, and 300 K, respectively. The geometries of single-molecules are relaxed until the force on each atom is less than 0.05 eV/Å. The spin-polarization transmission is calculated from

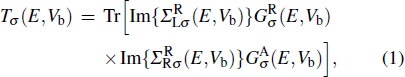
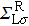
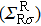
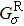
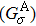
where π represents the α (β) spin state, the coupling function for the left (right) electrode, and the retarded (advanced) Green function.

3. Results and discussion

In Table 1, we first show the spin-filtering efficiencies (SPEs) of M-TPP(S)2 and M-TPP(SH)2 calculated from the formula

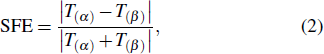
where T(α) and T(β) represent the transmission coefficients at the Fermi level for the α and β spin states of molecular junctions, respectively. For Co-TPP boned to gold electrodes through S- or SH-linkers, the spin-filtering effect is very weak. Clearly, the SPEs for Co-TPP(S)2 and Co-TPP(SH)2 are 4.6% and 6.6%, respectively. Thus there is no obvious difference between them. For V-TPP(S)2 and V-TPP(SH)2 [Mn-TPP(S)2 and Mn-TPP(SH)2], though their SPEs are higher, the hydrogen at the gold–sulfur interface does not cause a significant difference between them. However, the SPEs of Cr-TPP(S)2 and Cr-TPP(SH)2 show a significant difference. A similar situation can also be observed in Mn-TPP. It is found from Table 1 that the SPE is only ∼ 48.4% in the Au–SR bonding case, indicating that its application value is limited. However, a nearly perfect spin-filtering effect can be observed when Mn-TPP is bonded to gold electrode through Au–S(H)R bonding. Therefore, the hydrogen at the gold–sulfur interface may play an important role in determining electron spin polarization of M-TPP-based single-molecule junctions, depending on the type of transition metal ions embedded into porphyrin ring. These results also indicate that the nature of gold–sulfur interface can be identified in experiment through detecting spin-filtering signal, and Cr-TPP and Mn-TPP are potential candidate molecules for identifying the hydrogen atom.

Table 1.

Spin-filtering efficiencies of M-TPP-based molecular junctions through Au–SR and Au–S(H)R bondings.

.

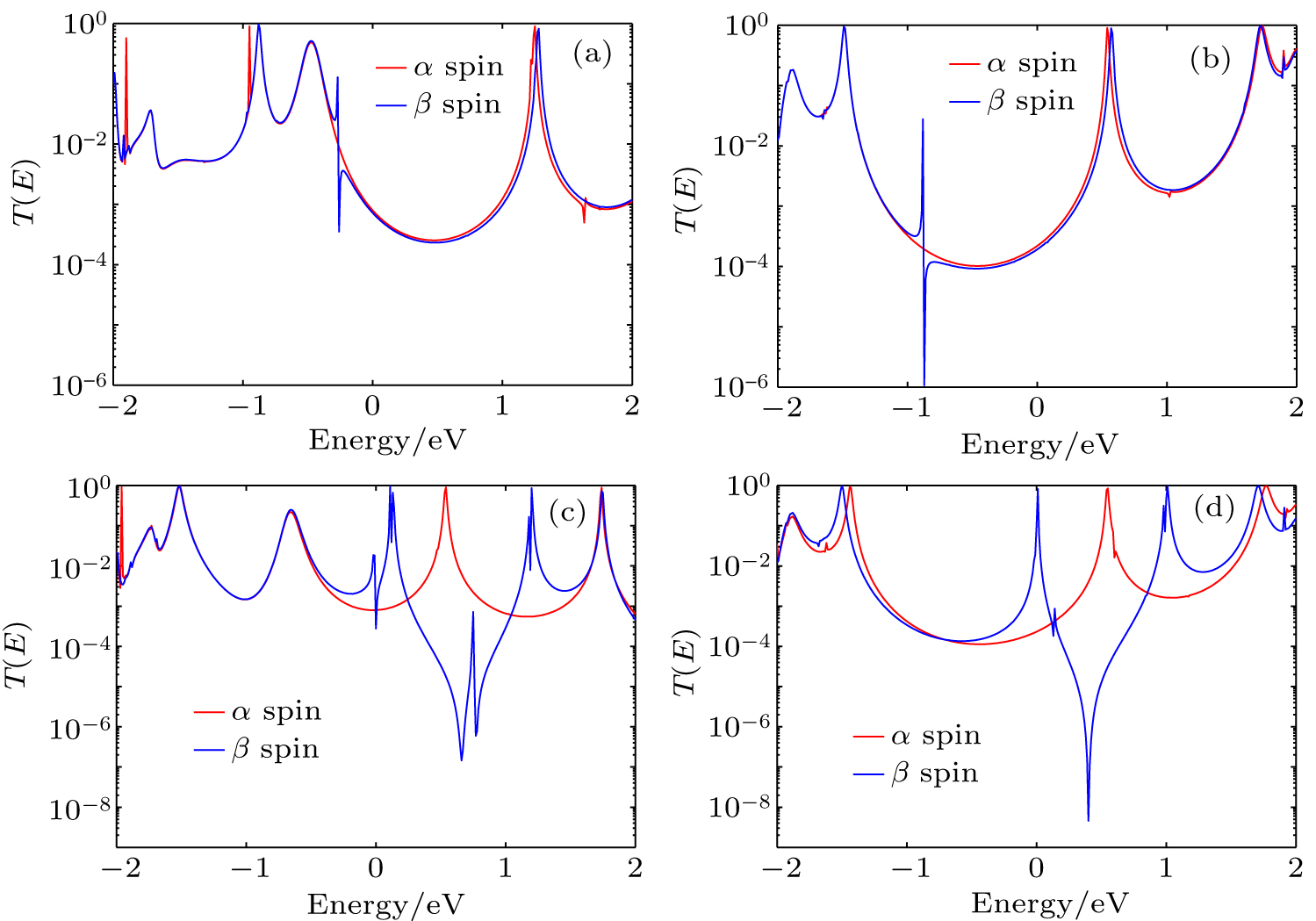
We take Co-TPP and Mn-TPP for examples to investigate the effect of the hydrogen attached to the sulfur on the spin-filtering. Figures 2(a) and 2(b) show the spin-polarized transmission spectra of Co-TPP(S)2 and Co-TPP(SH)2, respectively. It is found that for Co-TPP(S)2, the spin-polarized transmission peaks in both spin states occur in a higher or lower energy region, and the conductance difference at the Fermi level is small. In the Au–S(H)R bonding case, the retention of the hydrogen makes the transmission peaks of the α and β spin states simultaneously move to the lower energy region, and the characteristic of electron spin polarization is not obvious near the Fermi level. Thus, the SPE of Co-TPP(SH)2 almost keeps unchanged compared with that of Co-TPP(S)2. The situation is different in the molecular junction incorporating Mn-TPP. Figures 2(c) and 2(d) display the spin-polarized transmission spectra of Mn-TPP(S)2 and Mn-TPP(SH)2, respectively.

Fig. 2. Spin-resolved transmission spectra of (a) Co-TPP(s)2, (b) Co-TPP(SH)2, (c) Mn-TPP(s)2, and (d) Mn-TPP(SH)2 at zero bias.

Moreover, in Table 2, we also present the energy positions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) for Mn-TPP(S)2 and Mn-TPP(SH)2. It is found from Fig. 2(c) that for the α spin state of Mn-TPP(S)2, the transmission peaks on both occupied side and unoccupied side are away from the Fermi level, leading to a low conductance at the Fermi level. For the β spin state of Mn-TPP(S)2, the transmission near the Fermi level is dominated by HOMO, LUMO, and LUMO +1 [see Fig. 2(c) and Table 2]. Clearly, there are three-transmissional peaks lying near the Fermi level. However, the Fermi energy is located at the tail of HOMO- and LUMO-channeled transmission peaks, and its conductance is also low. Thus, the corresponding SPE is low in Mn-TPP(S)2. However, the conductance difference between the α and β spin states is obvious when Mn-TPP is bonded to gold electrode through Au–S(H)R bonding. For the α spin state of Mn-TPP(SH)2, the transmission peaks are still far away from Fermi level, which is similar to the scenario of Mn-TPP(S)2. For the β spin state of Mn-TPP(SH)2, though the transmission peaks on the occupied side are far away from the Fermi level, the LUMO-channeled transmission peak is very close to the Fermi level. As a consequence, the spin-filtering effect with the coexistence of conducting characteristic in the β spin state and nearly insulating characteristic in the α spin state is observed in Mn-TPP(SH)2.

Table 2.

Energy positions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) for Mn-TPP(S)2 and Mn-TPP(SH)2.

.

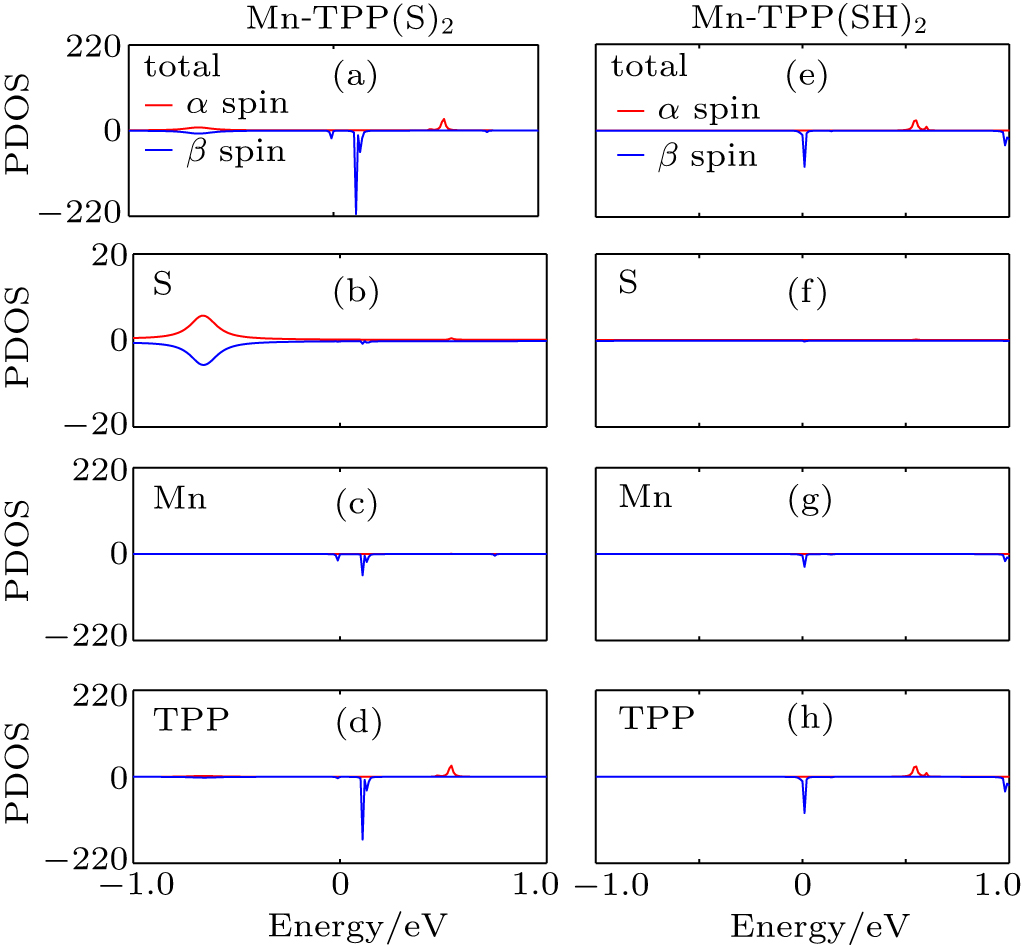
In order to probe the origin that the retention of the hydrogen drastically changes the SPE of the molecular junction incorporating Mn-TPP, the density of states (DOS) is calculated from the trace of the retarded Green’s function. In Figs. 3(a) and 3(e), we present DOS projected onto the central molecule of Mn-TPP(S)2 [Mn-TPP(SH)2]. Moreover, in Figs. 3(b)–3(d) [Figs. 3(f)–3(h)], we also present DOS projected onto S, Mn, and TPP of Mn-TPP(S)2 [Mn-TPP(SH)2]. It is found from Fig. 3(a) that for the α spin state of Mn-TPP(S)2, the incoming electrons are blocked near the Fermi level due to the lack of available states. This situation is still maintained in the Au–S(H)R bonding case as shown in the upper part of Fig. 3(e). In the β spin state of Mn-TPP(S)2, the HOMO and the LUMO, which mainly originate from the coupling between π electrons of C and N atoms in the molecular backbone and the 3d electrons of Mn atom, dominate the electron transport near the Fermi level. The π–d hybridization in the LUMO is stronger than that in the HOMO as shown in the lower part of Figs. 3(c) and 3(d). In the Au–S(H)R bonding case, the presence of extra electrons will rearrange the electron density of Mn-TPP. For M-TPP-based (M = V, Cr, Mn, Fe, and Co) molecular junctions, we calculate the magnetic moment change of M between the Au–SR bonding case and the Au–S(H)R bonding case by using Mulliken population analysis. Calculation results indicate that the largest magnetic moment change belongs to the Mn atom in Mn-TPP, there is a 0.115 μB increase compared with that in the Au–SR bonding case. Thus the retention of the hydrogen leads to a significant effect on 3d electron states of Mn atom. Clearly, we observe the disappearance of Mn 3d electrons featured HOMO state, as shown in the lower part of Figs. 3(c) and 3(g). For the LUMO state, however, the Mn 3d electron is still involved in the covalent coupling with 2p electrons of C and N atoms in the molecular backbone [see the lower part of Figs. 3(g) and 3(h)]. Meanwhile, it is also noted that the LUMO moves toward the Fermi level. Moreover, we find from Figs. 3(b) and 3(f) that the highest occupied electronic state of S atoms becomes depressed due to the hydrogen is retained. However, the corresponding electronic state is away from the Fermi level, and does not play a leading role in the transmission spectra near the Fermi level.

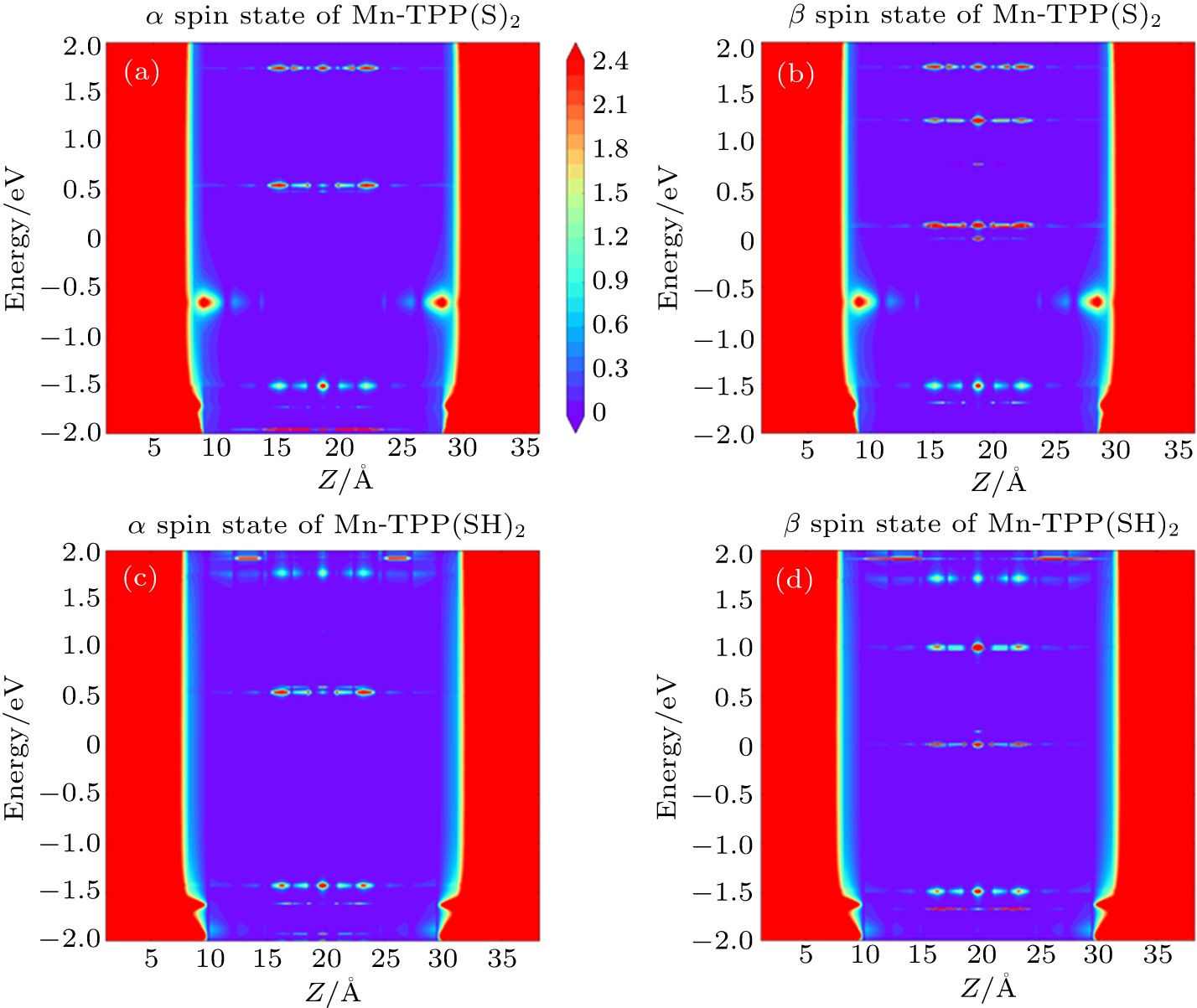
Fig. 3. (a) [(e)] Atomic sites projected DOS of central molecule in the Mn-TPP-based molecular junction through Au–SR [Au–S(h)R] bonding, and atomic sites projected DOS of (b) [(f)] S, (c) [(g)] Mn, and (d) [(h)] TPP in the Mn-TPP-based molecular junction through Au–SR [Au–S(h)R] bonding.

To further reveal the effect of the hydrogen atom at the gold–sulfur interface on SPE, in Fig. 4, we present the position-dependent local DOS from the left end to the right end of the central scattering region in Mn-TPP(S)2 and Mn-TPP(SH)2. From Fig. 4(a), it is found that in the α spin state of Mn-TPP(S)2, the LUMO only broadens slightly but display a delocalized characteristic over the central molecule. While the situation for HOMO is opposite to that for the LUMO. Thus a sharp LUMO-channeled transmission peak and a broadened HOMO-channeled transmission peak simultaneously occur in the α spin state of Mn-TPP(S)2 as shown in Fig. 2(c). However, the HOMO and the LUMO are away from the Fermi level, leading to low admittance of incoming electrons at the Fermi energy. In the β spin state of Mn-TPP(S)2, both of HOMO and LUMO are close to the Fermi level, especially for the HOMO. However, the HOMO is broadened to a lower extent than the LUMO [see Fig. 4(b)]. It is also noted that the hybridization between the HOMO and electrode state is very weak. As a consequence, the low admittance of incoming electrons is still observed in the β spin state of Mn-TPP(S)2 as shown in Fig. 2(c). The situation in the Mn-TPP(S)2 is different from that in Mn-TPP(SH)2. It is found from Fig. 4(c) that in the α spin state of Mn-TPP(SH)2, the LUMO and the HOMO display a relatively delocalized nature, resulting in high transmission peaks [see Fig. 2(d)]. However, the HOMO in the Au–S(H)R bonding case moves up relative to that in the Au–SR bonding case, leading to lower transmission value near the Fermi level. For the β spin state of Mn-TPP(SH)2, the hydrogen atom at the gold–sulfur interface only slightly changes the position of the HOMO and the position of the LUMO compared with that of Mn-TPP(S)2 [see Table 2]. But the HOMO becomes strongly localized [not visible on the scale of Fig. 4(d)]. For the LUMO, however, it not only maintains a relatively delocalized feature, but also further approaches to the Fermi level. This results in a high LUMO-channeled transmission peak at 0.01 eV as shown in Fig. 2(d). Thus, the electron transmission probability at the Fermi energy is significantly enhanced. The huge conduction difference between the α and β spin state of Mn-TPP(SH)2 gives rise to a nearly perfect spin filtering effect.

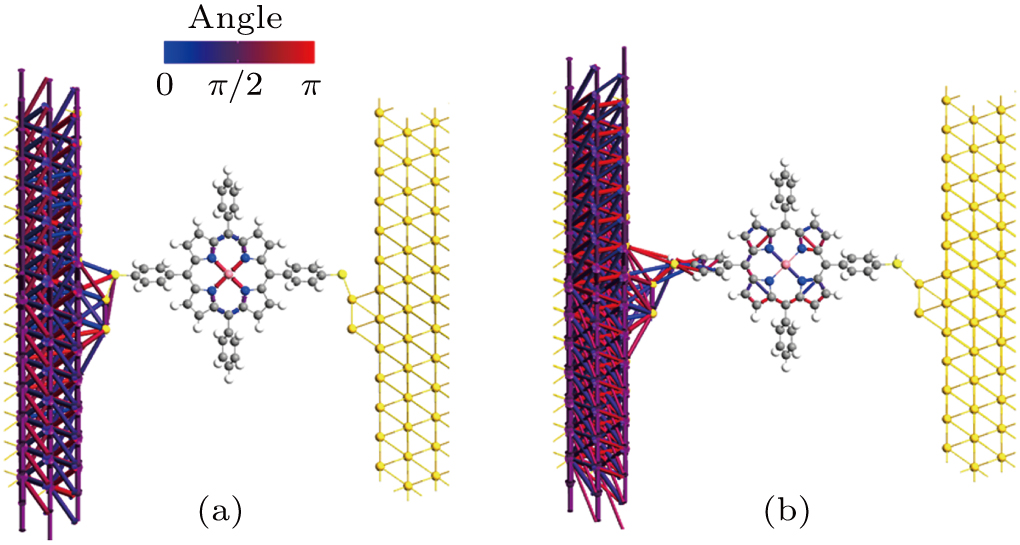
Fig. 4. Position-dependent local DOS from the left end to the right end of the central scattering region in (a) [(c)] α and (b) [(d)] β spin state of Mn-TPP(s)2 [Mn-TPP(SH)2].

In Figs. 2(a) and 2(b), it is found that for the β spin state of Co-TPP(S)2 and Co-TPP(SH)2, there is no obvious difference in transmission near the Fermi energy. However, the hydrogen atom attached to the sulfur has a significant effect on the spin-dependent transmission dips induced by the quantum interference on the occupied side. Clearly, the transmission coefficient of the dip in the β spin state of Co-TPP(SH)2 is two orders of magnitude lower than that of Co-TPP(S)2. When the Co-TPP-based molecular junction is considered as a gate-regulated switching device, the Au–SR bonding case is predicted to limit its practical application value, but the Au–S(H)R bonding case is believed to have potential to initiate a new exciting application in the future. The result also indicates that the spin-dependent antisresonance is highly sensitive to the characteristics of the electrode-molecule contact, and more suitable to being used as a key signature of gold–sulfur interface identification in the Co-TPP-based single-molecule junction. To explore the origin of this difference in the Au–SR and Au–S(H)R bonding cases, in Fig. 5, we plot the interatomic transmission paths at the energy of the transmission dips. It is can be seen from Fig. 5(a) that in the Au–SR bonding case, the transmission shows the reversal of ring currents near the metal center as displayed by blue, purple, and red arrows. Especially impressive is that the ring currents in the central region present mirror symmetry about the Co atom. The reversal of ring currents is confirmed to be a clear signature of quantum interference effect, which is similar to the result reported previously.[15] For the Au–S(H)R bonding case, it is found that quantum interference is mainly mediated by the molecular backbone but not the metal center. Clearly, here, the ring-current reversal phenomena mainly concentrate in pyrrole rings, showing an obvious difference from the Au–SR bonding case. Thus, the retention of the hydrogen at the gold–sulfur interface tunes the main transmission pathways, which may lead to a large difference in transmission value of dip between the Au–SR and Au–S(H)R bonding case.

Fig. 5. (a) Interatomic transmission pathway at –0.26 eV for β spin state of Co-TPP(s)2, and (b) interatomic transmission pathway at –0.87 eV for β spin state of Co-TPP(SH)2. Arrow color means direction of electron transport.

To further explore the effect of the hydrogen atom at the gold–sulfur interface on transmission dip, the transmission eigenvalues at the energy of the transmission dip for the β spin state of Co-TPP(S)2 and Co-TPP(SH)2 are calculated, and the corresponding eigenfunctions of transmission eigenchannels are also plotted in Fig. 6. Moreover, the eigenfunctions of transmission eigenchannels at the Fermi level for the β spin states of Co-TPP(S)2 and Co-TPP(SH)2 are also presented for comparison. At the Fermi energy, though there are multiple transmission eigenvalues for the Au–SR and Au–S(H)R bonding case, only the first transmission eigenchannel is open. Clearly, the hydrogen atom attached to the sulfur only slightly weakens the delocalization degree of the first transmission eigenchannel, and thus the transmission difference at the Fermi level is not obvious between the β spin states of Co-TPP(S)2 and Co-TPP(SH)2 as shown in Figs. 2(a), 2(b), and 6. At the energy postions of transmission dips, multiple transmission eigenvalues are also observed for Co-TPP(S)2 and Co-TPP(SH)2, but only the first two transmission eigenchannels are of significant weight. For Co-TPP(S)2, it can be seen from Fig. 6 that for these two transmission eigenchannels, eigenstate amplitude is dominated by the left Au screening layer, the S atom, the left phenyl moiety, the pyrrole rings, and the Co atoms. Further observation shows that the polarization characteristic of charge density for the first eigenchannel is slightly stronger than that for the second eigenchannel, indicating a small difference between their delocalization degrees. For the Co-TPP(SH)2, however, the first transmission eigenchannel is strongly localized at the gold–sulfur interface and the Co atoms. While for the second transmission eigenchannel, it still maintains a relatively delocalized characteristic. Therefore, at the –0.87 eV, the coexistence of strongly localized characteristics in one transmission eigenchannel and relatively delocalized in the other transmission eigenchannel makes the quantum interference very obvious,[32] resulting in very low transmission in the dip [see Fig. 2(b)].

Fig. 6. Eigenfunctions of transmission eigenchannels for β spin states of Co-TPP(s)2 and Co-TPP(SH)2 at Fermi energy and the energy values of transmission dips, with isovalue being set to be 0.1.
4. Conclusions

In this work, a comparative study of spin transport in M-TPP-based single-molecule junctions through Au–SR and Au–S(H)R bonding is performed by using nonequilibrium Green’s function in combination with the density functional theory. We theoretically demonstrate that the hydrogen atom at the gold–sulfur interface may dramatically affect spin-filtering efficiency of M-TPP-based single-molecule junctions, depending on the type of transition metal ions embedded into porphyrin ring. Moreover, we also find that for Co-TPP-based single-molecule junctions, the spin-dependent transmission dips induced by the quantum interference also display an obvious difference between the Au–SR and Au–S(H)R bonding case. This is due to the fact that at the energy position of the transmission dip, the retention of the hydrogen makes the first transmission eigenchannel strongly localized. Thus, the strongly localized and relatively delocalized transmission eigenchannels are coexistent at the same energy position, leading to very low transmission in the dip. These results indicate that the fate of hydrogen should be concerned in the theoretical model according to the actual preparation condition, which is important for our judgment on the application value of single-molecule spintronic devices. Our study also indicates that it is possible to identify the nature of gold–sulfur interface of the single-molecule junction with spin-polarized transport by using the signatures of spin-filtering and spin-dependent antiresonance.

Reference
[1] Ke G Duan C Huang F Guo X 2020 InfoMat 2 92
[2] Andres R P Bein T Dorogi M Feng S Henderson J I Kubiak C P Mahoney W Osifchin R G Reifenberger R 1996 Science 272 1323
[3] Kuang G Chen S Z Yan L Chen K Q Shang X Liu P N Lin N 2018 J. Am. Chem. Soc. 140 570
[4] Jia C Migliore A Xin N Huang S Wang J Yang Q Wang S Chen H Wang D Feng B Liu Z Zhang G Qu D H Tian H Ratner M A Xu H Q Nitzan A Guo X 2016 Science 352 1443
[5] Xin N Wang J Jia C Liu Z Zhang X Yu C Li M Wang S Gong Y Sun H Zhang G Liu Z Zhang G Liao J Zhang D Guo X 2017 Nano Lett. 17 856
[6] Zeng J Chen K Q Tong Y X 2018 Carbon 127 611
[7] Zhang Z Guo C Kwong D J Li J Deng X Fan Z 2013 Adv. Funct. Mater. 23 2765
[8] Qiu M Zhang Z H Deng X Q Pan J B 2010 Appl. Phys. Lett. 97 242109
[9] Kuang G Chen S Z Wang W Lin T Chen K Shang X Liu P N Lin N 2016 J. Am. Chem. Soc. 138 11140
[10] Pan C N Long M Q He J 2018 Chin. Phys. 27 088101
[11] Zeng Y J Liu Y Y Zhou W X Chen K Q 2018 Chin. Phys. 27 036304
[12] Gu Y Hu Y Huang J Li Q Yang J 2019 J. Phys. Chem. 123 16366
[13] Yang K Chen H Pope T Hu Y Liu L Wang D Tao L Xiao W Fei X Zhang Y Y Luo H G Du S Xiang T Hofer W A Gao H J 2019 Nat. Commun. 10 1
[14] Zeng J Chen K Q 2020 J. Mater. Chem. 8 3758
[15] Garner M H Li H Chen Y Su T A Shangguan Z Paley D W Liu T Ng F Li H Xiao S Nuckolls C Venkataraman L Solomon G C 2018 Nature 558 415
[16] Shi X Dai Z Zeng Z 2007 Phys. Rev. 76 235412
[17] Cai S Deng W Huang F Chen L Tang C He W Long S Li R Tan Z Liu J Shi J Liu Z Xiao Z Zhang D Hong W 2019 Angew. Chem. 131 3869
[18] Frisenda R Janssen V A E C Grozema F C van der Zant H S J Renaud N 2016 Nat. Chem. 8 1099
[19] Pilevarshahri R Rungger I Archer T Sanvito S Shahtahmassebi N 2011 Phys. Rev. 84 174437
[20] Tsuji Y Staykov A Yoshizawa K 2011 J. Am. Chem. Soc. 133 5955
[21] Cho W J Cho Y Min S K Kim W Y Kim K S 2011 J. Am. Chem. Soc. 133 9364
[22] Han L Zuo X Li H Li Y Fang C Liu D 2019 J. Phys. Chem. 123 2736
[23] Deng X Zhang Z Zhou J Qiu M 2010 Appl. Phys. Lett. 97 143103
[24] Kwong G Zhang Z Pan J 2011 Appl. Phys. Lett. 99 123108
[25] Xie F Fan Z Q Chen K Q Zhang X J Long M Q 2017 Org. Electron. 50 198
[26] Fan Z Q Zhang Z H Qiu M Deng X Q Tang G P 2012 Appl. Phys. Lett. 101 073104
[27] Qiu M Zhang Z Fan Z Deng X Pan J 2011 J. Phys. Chem. 115 11734
[28] Zeng J Chen K Q 2017 Phys. Chem. Chem. Phys. 19 9417
[29] Häkkinen H 2012 Nat. Chem. 4 443
[30] Inkpen M S Liu Z F Li H Campos L M Neaton J B Venkataraman L 2019 Nat. Chem. 11 351
[31] Brandbyge M Mozos J L Ordejón P Taylor J Stokbro K 2002 Phys. Rev. 65 165401
[32] Hong K Kim W Y 2013 Angew. Chem. 125 3473