† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11704058 and 11974069), the National Special Support Program for High-level Personnel Recruitment, China (Grant No. W03020231), Liaoning Revitalization Talents Program, China (Grant No. XLYC1902113), Program for Liaoning Innovation Team in University, China (Grant No. LT2016011), Science and Technique Foundation of Dalian, China (Grant No. 2017RD12), and Fundamental Research Funds for the Central Universities, China (Grant No. DUT19RC(3)007).
Quantum theory of surface plasmons is very important for studying the interactions between light and different metal nanostructures in nanoplasmonics. In this work, using the canonical quantization method, the SPPs on nanowires and their orbital and spin angular momentums are investigated. The results show that the SPPs on nanowire carry both orbital and spin momentums during propagation. Later, the result is applied to the plasmonic nanowire waveguide to show the agreement of the theory. The study is helpful for the nano wire based plasmonic interactions and the quantum information based optical circuit in the future.
It is well known that surface plasmons polaritons (SPPs) existing at interfaces between metals and dielectrics are coherent collective oscillation of free electrons (with coupled electromagnetic field) at the surface of metal. The unique properties of plasmons on nanoscale metallic systems have produced a number of dramatic effects and interesting applications, such as molecule detection with surface-enhanced Raman scattering,[1–3] biosensing,[4,5] waveguiding,[6–8] enhanced interactions,[9,10] and switching devices below the diffraction limit.[11,12] Plasmonic nanowires have been attracting a lot of attention as SPP waveguides, analogy to optical fiber waveguides but within a hundred nanometers scale cross section, which breaks the diffraction limit. The strong confinement and small mode volume of plasmonic wires facilitate the strong coupling between quantum emitters and nanowire,[13,14] the low Q factor Fabry–Pérot resonator,[15] and nanowire-wire based plasmonic devices and chips.[11,16,17] The properties of keeping quantum information like entanglement of plasmonic waveguides[18–21] now have the potential applications in quantum information and fundamental researches.
Surface plasmons are quantized electric charge density waves, while usually a lot of the phenomena can be illustrated with classical Maxwell equations in this boosting area in the past twenty years.[22] In the meantime, quantum theory descriptions were also developed to explain the phenomena such as non-locality,[23] tunneling,[24,25] hot electrons,[26–28] and so on.[29] Especially quantization of surface plasmons for common systems like plane metal interface[30] and nanoparticle[31] has been developed to deal with the interactions between the plasmons and the surrounding molecules,[32–34] which is, in a lot of conditions, beyond the Maxwell’s theory. Now quantum plasmonics has been a rapid growing field that involves the study of the quantum properties of SPs and their interaction with matters at the nanoscale.[35]
The quantization process was usually performed by quantizing the electric field or considering the hydrodynamics meantime. Using Hopfield’s approach,[36] Elson and Ritchie reported the quantization scheme for SPPs on a metallic surface considering the hydrodynamics.[37] Archambault et al. reported the quantization scheme of the surface wave on a plane interface without any specific model of the dielectric constant.[38] Huttner and Barnett introduced a new quantization method by extending Hopfield’s approach to polaritons in dispersive and lossy media.[39] In Archambault’s works, they redid the quantization of the plasmons on plane interface in modern fashion for explaining the spontaneous and stimulated emission of SPPs.[38] Waks have re-quantized plasmons on nanoparticles under quasi-static approximation for describing the coupling of a dipole and a particle. And in Boardman’s work, the SPPs in different typical coordinates were dealt in common way with Bloch hydrodynamical model.[40] However, quantization of SPPs on cylindrical nanowires needs more investigation to illustrate more details and phenomena.
In this paper, a quantization scheme of SPPs on a cylindrical nanowire waveguide is introduced. The canonical quantization method is used, which is to identify the generalized coordinates and conjugate momentums. After getting the expressions in Fock states, the orbital and spin angular momentums are deduced. With the results one will find that the modes on the nanowire waveguide carry both orbital and spin angular momentums, which is consistent with the classic theory result from Picardi.[41] Following that, the formulas are applied to describe the SPPs on a nanowire in the waveguide, which shows good agreement. With the properties, SPPs on nanowires can easily carry quantum information and keep the entangle properties of the incident light.[20,42–44] The results will be very helpful in the quantum information and light–matter interactions research.
Let us consider SPPs propagating on the interface of a cylindrical metal nanowire (

To simplify the process in the following, the electromagnetic scalar and vector potentials Φ and A working in Coulomb q gauge (Φ = 0, ∇ ⋅ A = 0) are introduced here. With 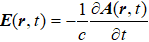
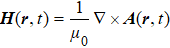
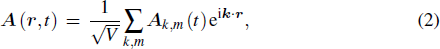




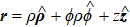
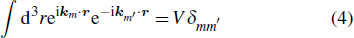

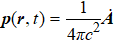


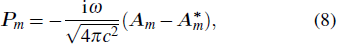






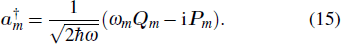
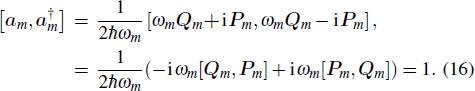


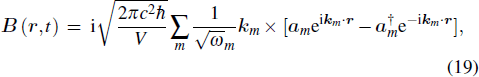

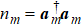


We set 


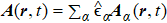

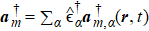
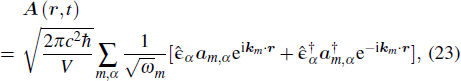



With the above results we will discuss the quantized field properties in the nanowire, such as spin and orbital angular momentums (SAM/OAM) and polarization. It has been known that the optical angular momentum is
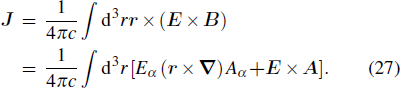
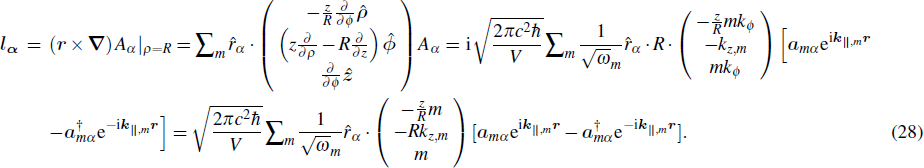


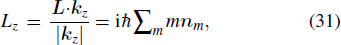

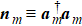
In the above expressions, one can rewrite the phase factor




The spin angular momentum density is


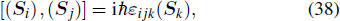

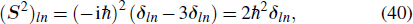


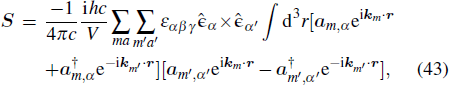

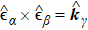
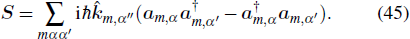
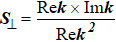
For plane waves, polarization is usually defined as 




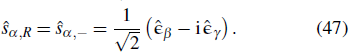

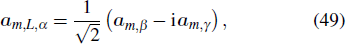



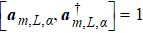
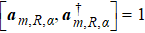
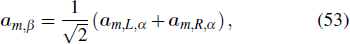


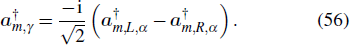


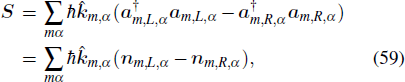


The nanowires performed as plasmonic waveguides are usually in homogeneous medium and excited with light perpendicular to the wire axis on one end.[6] The local symmetry at the terminus of the wire is broken when the SPPs are excited, so the phase factor eimϕ becomes cos (mϕ) or sin (mϕ). For thin wires, the higher-order modes |m| ⩾ 2 are cut off.[14] And the retardation effects are significant, which will cause the excitation phase difference for | m | = 0 and | m | = 1 modes as shown in Fig.


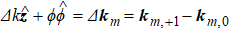

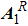
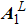

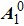
With the vector potential, one can directly achieve the following results in Fock states:








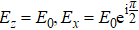

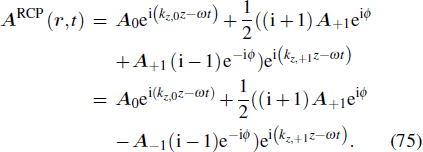
From the expression one can see that the pattern should be the superpostion of the two helical modes m = +1 and m = –1. It is also consist with the fact that the circularly polarized light can be decomposed with two orthorgnal linearly polarized light for the exciting light.
For LCP light excitation on one end, similarly we have






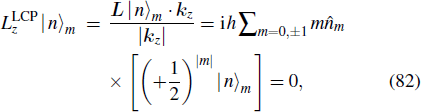
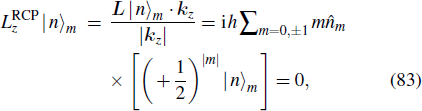


In the above, the electromagnetic modes of the plasmonic cylindrical wire are deduced and quantized, which are consistent with the quantized charge density wave on the wire with hydrodynamic method[40,49] due to all of the charge responses in optics are included in the permittivity of the material. One can see that the spin of SPPs on the wire contains both transverse components, which agrees with the conclusion of SPPs on plane surface.[46,50–52] The longitudinal components may be from the curvature boundary of the wire.[53] The higher modes also carry orbital angular momentums, which is very similar to the vortex wave. Along the wire, the orbital angular momentum quantum number can be 0 ±, 1± 2,…. Experimentally, it can be verified by putting the nanowire in homogeneous medium and the helix can be shown with quantum dots.[16] The momentum can be observed by using leakage Fourier transform microscope.[54] The spin-based effects also have an unprecedented potential to control light and its polarization, thereby promoting the research of optical chirality. The spin angular momentum and the orbital angular momentum will have coupling[46] and cause some other effects on the nanowire waveguide. In the experiment, the wires are sure with limited lengths. If the wire is not very long, the SPPs will be reflected by the other end and form standing waves, which are like a Fabry–Pérot cavity.[7] When it interacts with other systems like atoms or quantum dots, some hyperfine phenomenon may be expected.[55,56] In the above calculations, the dissipation of the nanowire material is ignored. However, if the imaginary part of the permittivity is considered (lossy medium), the commutation relation for canonical coordinate and momentum is not available any more, and the commutation relation for the creation and annihilation operators will have a decay coefficient. When the decay term is absorbed in the operators, all of the quantities will include the decay effect, and the ground state energy is also decaying because of the damping.
In this work, the electromagnetic modes on a plasmonic cylinder waveguide are quantized. The orbital and spin angular momentums are studied and it can be seen that similar to the vortex waves, the plasmon modes on cylinder nanowires carry both orbital angular momentum and spin angular momentum. The results may be helpful for the future quantum information applications.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] |






