The ferromagnetic Heusler-based shape memory alloys (FSMAs)^[1] which is a large family of multifunctional materials have been well studied both theoretically and experimentally. Introducing the external fields, the martensitic transformation (MT) will happen with the change of magnetic states from ferromagnetic (FM) state and antiferromagnetic/paramagnetic (AFM/NM) state. In the process of FMMT, there are usually accompanied by various physical properties, such as magnetic-field-induced recovery, magnetocaloric effect, barocaloric effect, exchange bias, magnetoresistance, and magnetostrain.^[2–19]

Recently, the all-d-metal Heusler-like alloys based on d–d hybridization by substituting transition metal (TM) with less valence electrons for main group element in classic Heusler alloys were reported.^[20,21] The metamagnetic MTs and corresponding multifunctional properties (magnetic-entropy change,^[20] field-induced strain,^[21] giant elastocaloric effect^[11,22,23]) were gained in MnNiTi(Co) system. Wei^[22] reported a reversible elastocaloric effect with ΔT_ad = 9.0 K at a strain level of 4.6% for Ni₃₅Co₁₅Mn₃₅Ti₁₅. Aznar^[23] reported a giant barocaloric effect for Ni₅₀Mn_31.5Ti_18.5, which has maximum value of adiabatic temperature (12 K) and isothermal entropy changes (74 J⋅kg⁻¹ ⋅ K⁻¹) under 4 kbar (1 bar = 10⁵ Pa). More ferromagnetic MT behaviors^[24–26] were also reported in other MnNiTi(Co) system. The exploration and design of new all-d-metal Heusler alloys has become a research hotspot.

Afterward, the crystal and electronic structures and MTs were predicted in Mn-based, Ni-based, and Pd-based all-d-metal Heusler alloys by first-principles calculations.^[27–30] Among the Heusler-based alloys, the Zn-based and Cd-based materials are less investigated in comparison with the other d-metals. This is probably due to the high vapor pressure (low boiling point)^[31–33] of these metals which makes them difficulty to be fabricated. Thus the first-principles calculations become an effective method to predict crystal structure and phase stability. Recently, Han et al.^[34] found that the Zn₂MnTM crystalize L2₁-type structure with ferromagnetic state, Zn₂RuMn, Zn₂RhMn, Zn₂OsMn, and Zn₂IrMn have possible MT. Yang et al.^[35] reported the atomic configurations, electronic, magnetic, mechanical, and dynamic properties for Cr₂ZnSi/Cr₂ZnGe.

In this work, we investigated the electronic structures, magnetic properties, and martensitic transformation in Cd-based all-d-metal Heusler-like alloys Cd₂MnTM (TM = Fe, Ni, Cu) by first-principles calculations. And we found that three samples reveal the ferromagnetic state with L2₁-type structure, and the Cd₂MnFe and Cd₂MnNi may possess the ferromagnetic martensitic transformation.

The Cambridge Serial Total Energy Package (CASTEP) code, based on pseudopotential method with a plane-wave basis set, was used to investigate the electronic structures, magnetic properties, and MT of all-d-metal Heusler-like alloys Cd₂MnTM (TM = Fe, Ni, Cu).^[36,37] The generalized-gradient-approximation (GGA)^[38] and ultra-soft pseudo-potential^[36] were selected to carry out the electron-exchange-related energy and interaction between atomic core and valence electrons, respectively. A 500-eV plane basis set energy cut-off and the Monkhorst–Pack special 16×16×16 k-point mesh were used in the irreducible Brillouin zone. The selected energy convergence and self-consistent field tolerances were within 1 × 10⁻⁶ eV/atom and 1 × 10⁻⁷ eV/atom, respectively.

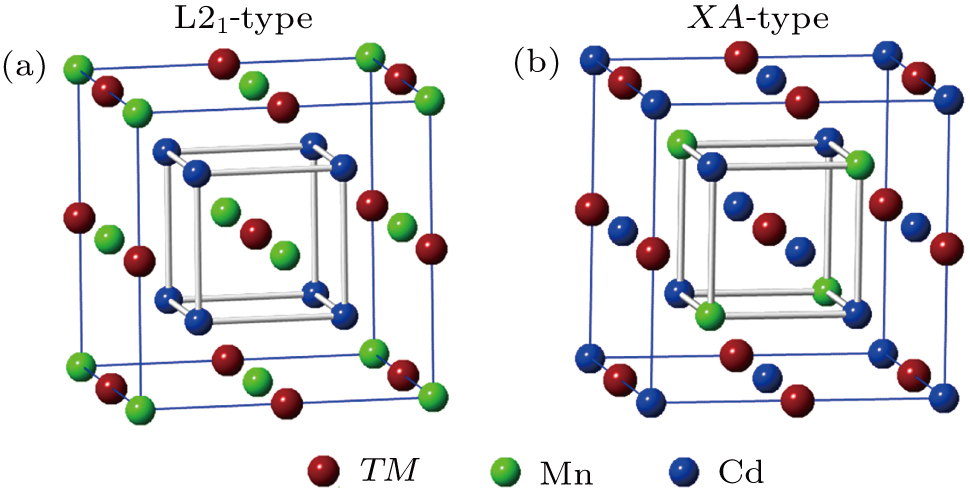
The classic full-Heusler alloys X₂YZ (X and Y are TM atoms, Z is main group atom) have the highly ordered structures, there are four atom sites occupied the atoms, namely, A (0,0,0), B (0.25,0.25,0.25), C (0.5,0.5,0.5), and D (0.75,0.75,0.75). Normally, there are two possible atomic-site orderings on the basis of the site rule of Heusler alloys.^[39,40] The first is L2₁-type structure, in which two X atoms with higher valence electrons prefer to occupy sites A and C, Y atom with fewer valence electrons prefers to occupy site B, main group atom Z prefers to occupy site D. The other is XA-type structure, in which two X atoms with fewer valence electrons prefer to occupy sites A and B, Y atom with higher valence electrons prefers to occupy site C, main group Z atom prefers to occupy site D. In our work, the main group atom Z is replaced by TM atom. The two crystal structures of Cd₂MnTM (TM = Fe, Ni, Cu) are shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) L21-type and (b) XA-type crystal structures of Cd2MnTM (TM = Fe, Ni, Cu) compounds.

The calculated total energy as a function of lattice constant for Cd₂MnTM (TM = Fe, Ni, Cu) is shown in Fig. 2. The ferromagnetic (FM), antiferromagnetic (AFM), nonmagnetic (NM) states in both crystal structures (L2₁-type and XA-type) were considered to evaluate the ground state of Cd₂MnTM (TM = Fe, Ni, Cu) alloys through geometric optimization. The lowest energy for all the alloys appears with the L2₁-type structure in FM state. The calculated equilibrium lattice constants are 6.49 Å, 6.44 Å, and 6.51 Å, respectively. The crystal structure, magnetic state, and equilibrium lattice constants are listed in Table 1. Therefore, we further select the FM L2₁-type structure in subsequent discussions to study other properties.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Calculated total energy as a function of lattice constant for (a) Cd2MnFe, (b) Cd2MnNi, and (c) Cd2MnCu with L21-type and XA-type structures in FM, AFM, and NM states, respectively.

Table 1.

Table 1.

Table 1. Crystal structure, equilibrium lattice constant (a), total and partial spin moments for Cd2MnTM (TM = Fe, Ni, Cu) at equilibrium lattice constant. . Compound Structure a/Å Mtot/μB MCd/μB MTM/μB MMn/μB Cd2MnFe L21-type 6.49 6.36 0.02 2.72 3.61 Cd2MnNi L21-type 6.44 3.95 0.02 0.19 3.72 Cd2MnCu L21-type 6.51 3.82 0.03 0.01 3.76

Table 1. Crystal structure, equilibrium lattice constant (a), total and partial spin moments for Cd2MnTM (TM = Fe, Ni, Cu) at equilibrium lattice constant. .

After geometric optimization, the band structures of L2₁-type Cd₂MnTM (TM = Fe, Ni, Cu) alloys were calculated (see Fig. 3) at their equilibrium lattice constants in cubic state. Based on the band structures of three alloys, the bands in spin-up and spin-down channels overlap with the Fermi level (E_F) indicates that all the alloys are typical metallic characterization. The degrees of overlap in spin-up channel are approximately the same, but the degrees of overlap in spin-down channel are obviously different. This difference in electronic structures corresponds to a huge difference in magnetism. As we all known, the electronic structures and magnetic properties are mainly determined by the electronics near E_F. Therefore, to further analyze magnetic properties, the calculated total density of states (TDOS) and partial density of states (PDOS) of L2₁-type Cd₂MnTM (TM = Fe, Ni, Cu) were performed, which are shown in Fig. 4. For all TDOS, the spin-up and spin-down bands go across E_F. Between –10 eV and –7 eV, there are a couple of symmetrical peaks in the spin-up and spin-down states, which are far from the E_F and come from the Cd d-states. Therefore, the Cd d-states have weak contributions to the total magnetic moments. For the region near Fermi level, the peaks appear at –4 eV to –1 eV in the spin-up direction and at –3 eV to +2 eV in the spin-down direction, which mainly come from the direct hybridizations between d-states of Mn and TM. The exchange splitting around the E_F of Cd₂MnFe in both spin states is stronger than that of Cd₂MnNi and Cd₂MnCu, since the spin-down DOS mainly locates above the Fermi level for Cd₂MnFe. Therefore, the spin magnetic moment of Cd₂MnFe is larger than that of other two alloys.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Calculated band structures of L21-type (a) Cd2MnFe, (b) Cd2MnNi, and (c) Cd2MnCu at each equilibrium lattice constant.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Calculated total and partial density of states of L21-type (a) Cd2MnFe, (b) Cd2MnNi, and (c) Cd2MnCu at each equilibrium lattice constant.

Furthermore, the structure instability of Cd₂MnFe comes from the sharp peak near E_F due to the energy increasing of the system.^[41] The structures of Cd₂MnNi and Cd₂MnCu are relatively stable duo to the valleys appear near E_F based on Jahn–Teller effect,^[42] the aspect of MTs will be discussed in the subsequent section. For the PDOS, the d-states of Cd locate below –7 eV and the p-states with low energy locate in the energy region from –4 eV to +2 eV. There are strong d–d orbital hybridizations between Mn and TM atoms from –4 eV to +2 eV. The hybridization between the p states of Cd and d states of other transition metal atoms can be expected. The Cd element acts as the main group element in the Heusler alloys, which is similar to Ga-based Heusler alloys.^[43] From the Fig. 4(a), the spin-down DOS mainly locates above the Fermi level, while the spin-up DOS mainly locates below the Fermi level, which results in the large spin splitting in two spin states for both Mn and Fe atoms and large spin magnetic moments from Mn and Fe atoms (3.61 μ_B and 2.72 μ_B, see Table 1), respectively. Therefore, Mn and Fe atoms make contributions considerably to the total magnetic moment. From Fig. 4(b) for Cd₂MnNi and Fig. 4(c) for Cd₂MnCu, compared with Mn atom, the Ni/Cu atom shows a relatively weak spin splitting in two spin states, there are a little spin magnetic moments from Ni and Cu atoms (0.19 μ_B and 0.01 μ_B, see Table 1), respectively. The total magnetic moments of Cd₂MnNi and Cd₂MnCu are contributed by Mn atoms only.

The total and atomic magnetic moments of L2₁-type (a) Cd₂MnFe, (b) Cd₂MnNi, and (c) Cd₂MnCu as a function of the lattice constant were calculated, as shown in Fig. 5. The total magnetic moments at equilibrium lattice constants are 6.36 μ_B, 3.95 μ_B, 3.82 μ_B, respectively, which are listed in Table 1. With increasing the lattice constant, the total magnetic moments slightly increase and keep at large values. The values of magnetic moments are 3.5 μ_B–4.0 μ_B for Mn atoms and 2.5 μ_B–3.0 μ_B for Fe atoms (Fig. 5(a)). The magnetic moments of Ni atoms (Fig. 5(b)) and Cu atoms (Fig. 5(c)) are near zero. The results are consistent with the analysis of DOS. Large magnetic moments come from the spin splitting around the E_F for Mn and Fe atoms. All these make Cd₂MnFe having the largest total moment in the three alloys.

Fig. 5.

	Figure Option ViewDownloadNew Window
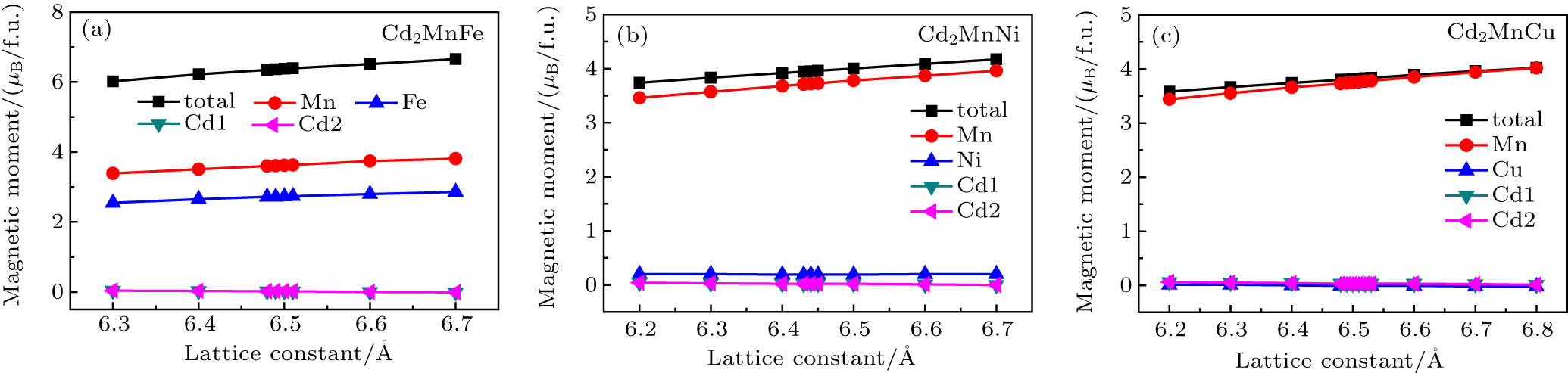	Fig. 5. Calculated total and atomic magnetic moments of L21-type (a) Cd2MnFe, (b) Cd2MnNi, and (c) Cd2MnCu as a function of the lattice constant.

To study the possibility of the MTs in Cd₂MnTM (TM = Fe, Ni, Cu) alloys, the energy difference (ΔE) between the tetragonal martensite and cubic austenite at the ground state as a function of c/a ratio (for c and a can be seen in Ref. [34]) with fixed crystal volumes, namely equilibrium cubic volume (V_opt) when c/a = 1, are given in Fig. 6. ΔE is a factor to determine whether the MT happens. The austenite is more stable than martensite when ΔE is less than zero, and vice versa. For Cd₂MnCu the minimum appears in c/a = 1, the ΔE is always above zero meaning that MT is unlikely to occur. The value of ΔE for Cd₂MnNi is the minimum (–0.04 eV) at c/a = 1.33. And for Cd₂MnFe, there are two minimum values, a shallow one in c/a < 1 and a deep one in c/a > 1. The shallow one is metastable phase, the most stable phase appears in c/a = 1.41 with the minimum (–0.19 eV). The negative values of ΔE imply that the alloys have a lower stability in austenitic phase, the total energy relax with changing the tetragonal distortion degree to a certain value of c/a, resulting in the MT happen for whole system.^[34,44,45] Therefore, Cd₂MnFe and Cd₂MnNi alloys would possess MTs. According to previous literature reports, the volume change based on the equilibrium lattice constant may influence the possible martensitic transformations,^[29,46] the energy difference (ΔE) as a function of c/a ratio with contraction/expansion of the unit cell volume (V_opt + x% V_opt, x = –3, –1, 0, 1, 3), for Cd₂MnTM (TM = Fe, Ni) were studied. The corresponding data are given in Fig. 7. It can also be clearly seen that the possible MT occurs because the curves maintain with the change of c/a for different x, the positions of metastable and most stable phases are unchanged. The value of ΔE decreases gradually from about –0.17 eV in the +3% volume phase to with about –0.21 eV in the –3% volume phase (inset of the Fig. 7), this can be a method for tuning the value of ΔE. It indicates that the –3% volume phase with ΔE = –0.21 eV is the most stable one among the uniform strain range.

Fig. 6.

	Figure Option ViewDownloadNew Window
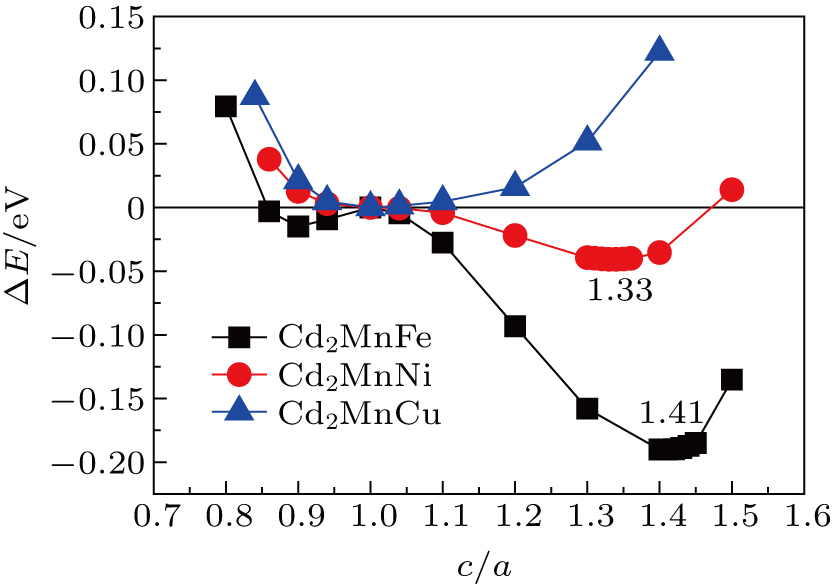	Fig. 6. ΔE as a function of the c/a ratio for Cd2MnTM (TM = Fe, Ni, Cu). The zero point represents the energy of the austenite (c/a = 1).

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. ΔE as a function of c/a ratio for Cd2MnFe with expansion/contraction of the unit cell volume. The zero point represents the energy of the austenite (c/a = 1). Inset: the relationship between ΔE and Vopt + x%Vopt.

Considering the magnetic moments of Cd₂MnTM (TM = Fe, Ni, Cu) with fixed volume, we carried out the total and atomic moments in the change of c/a. The band structures of Cd₂MnFe with c/a = 1.41 and Cd₂MnNi with c/a = 1.33 are shown in Figs. 8(a) and 8(b), respectively. The results indicate that the two alloys still show ferromagnetic character duo to the overlap between the Fermi level and the bands in spin-up and spin-down channels. The total magnetic moments in martensitic state decrease slightly compared to c/a = 1. Mn and Fe atoms make mainly contribution to total magnetic moments.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. (a) Calculated band structure of Cd2MnFe with c/a = 1.41. (b) Calculated band structure of Cd2MnNi with c/a = 1.33.

Figure 9 shows the total and atomic magnetic moments as function of c/a. With increasing the c/a, the total magnetic moment of Cd₂MnFe and atomic magnetic moments of Mn atom (3.39 μ_B–3.81 μ_B) and Fe atoms (2.55 μ_B–2.86 μ_B) are still large, which is preferable for the magnetostrictive behavior in martensitic state. The slightly decrease comes from decline of the magnetic moments of Fe and Mn atoms in martensitic state. For Cd₂MnNi and Cd₂MnCu, the values of total magnetic moments are stable in the c/a range of 0.85–1.10, increase of magnetic moments of Ni atoms for Cd₂MnNi and Mn atoms for Cd₂MnCu gives rise to slightly increase of total magnetic moments above c/a > 1.2. The magnetic moments of Cu and Cd atoms are almost unchanged (near zero) showing that it is insensitive to the change of c/a. Therefore, among the changing of c/a, total magnetic moments of Cd₂MnTM (TM = Fe, Ni, Cu) still maintain large values duo to the robust ferromagnetic exchange interaction. The total and partial magnetic moments of Cd₂MnTM (TM = Fe, Ni) in their martensitic phases are listed in Table 2.

Fig. 9.

	Figure Option ViewDownloadNew Window
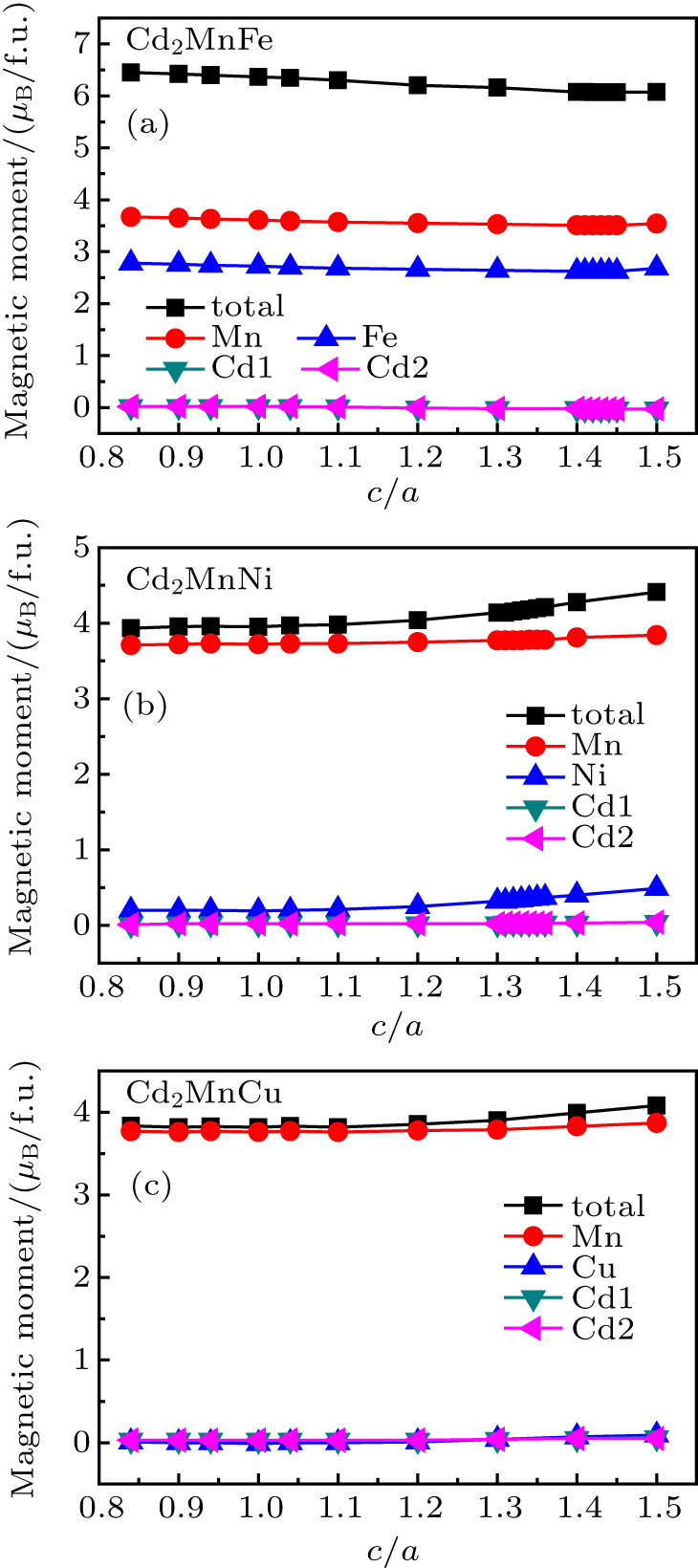	Fig. 9. Calculated total and atomic magnetic moments of L21-type (a) Cd2MnFe, (b) Cd2MnNi, and (c) Cd2MnCu as a function of c/a.

Table 2.

Table 2.

Table 2. Energy difference ΔE between martensite and austenite, c/a ratio, total and partial magnetic moments of Cd2MnTM (TM = Fe, Ni) in their martensitic phases. . Compound ΔE/eV c/a Mtot/μB MCd/μB MTM/μB MMn/μB Cd2MnFe −0.19 1.41 6.07 −0.03 2.62 3.51 Cd2MnNi −0.04 1.33 4.17 0.03 0.34 3.77

Table 2. Energy difference ΔE between martensite and austenite, c/a ratio, total and partial magnetic moments of Cd2MnTM (TM = Fe, Ni) in their martensitic phases. .

In summary, we have studied the electronic structures, magnetic properties, and martensitic transformation in all-d-metal Heusler-like alloys Cd₂MnTM (TM = Fe, Ni, Cu) by first-principle calculations. The ferromagnetic L2₁-type cubic structure is the most stable phase. Applying site rule of Heusler alloys, the two Cd atoms prefer to occupy the equilibrium A, C sites, Mn and TM atoms prefer to occupy the equilibrium B and D sites, respectively. The total magnetic moment at equilibrium lattice constant of Cd₂MnFe (6.36 μ_B) is larger than Cd₂MnNi (3.95 μ_B) and Cd₂MnCu (3.82 μ_B). The energy differences (ΔE) between martensite and austenite are negative in Cd₂MnFe and Cd₂MnNi under tetragonal distortion and different uniform strains, indicating the possible occurrence of the ferromagnetic martensitic transformation. The present theoretical investigation in Cd₂MnTM alloys would provide some valuable information for exploring new all-d-metal Heusler alloys.