Cite this Article
Xu Sen, Hu Yangming, Liang Yuan, Shi Chenfei, Su Yuling, Guo Juan, Gao Qilong, Chao Mingju, Liang Erjun. Negative thermal expansion of Ca2RuO4 with oxygen vacancies. Chinese Physics B, 2020, 29(8): 086501  
Permissions
Negative thermal expansion of Ca2RuO4 with oxygen vacancies
Xu Sen1, Hu Yangming1, Liang Yuan2, †, Shi Chenfei3, Su Yuling3, Guo Juan1, Gao Qilong1, Chao Mingju1, Liang Erjun1, ‡
Key Laboratory of Materials Physics of Education of China, School of Physics and Microelectronics, Zhengzhou University, Zhengzhou 450001, China
Department of Applied Physics, Donghua University, Shanghai 201620, China
School of Physics and Electronic Engineering, Zhengzhou University of Light Industry, Zhengzhou 450001, China

 

† Corresponding author. E-mail: yliang@dhu.edu.cn ejliang@zzu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11874328 and 11574276). The SXRD experiments were performed at the BL02B2 and BL04B2 of SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI; proposal Nos. 2019A1167, 2019A1095, and 2019A1340). We also acknowledge the help of Beamline Scientists Dr. Lirong Zheng (BSRF), Dr. Shogo Kawaguchi, and Dr. Koji Ohara (SPring-8).

Abstract

Oxygen vacancies have a profound effect on the magnetic, electronic, and transport properties of transition metal oxides but little is known about their effect on thermal expansion. Herein we report the effect of oxygen defects on the structure formation and thermal expansion properties of the layered perovskite Ca2RuO4 (CRO). It is shown that the CRO containing excess oxygen crystallizes in a metallic L-CRO phase without structure transition from 100 K to 500 K and displays a normal thermal expansion behavior, whereas those with oxygen vacancies adopt at room temperature an insulating S-CRO phase and exhibit an enormous negative thermal expansion (NTE) from 100 K to about 360 K, from where they undergo a structure transition to a high temperature metallic L-CRO phase. Compared to the L-CRO containing excess oxygen, the S-CRO structure has increasingly large orthorhombic strain and distinctive in-plane distortion upon cooling. The in-plane distortion of the RuO6 octahedra reaches a maximum across 260 K and then relaxes monotonically, providing a structure evidence for the appearance of an antiferromagnetic orbital ordering in the paramagnetic phase and the Ag phonon mode suppression and phase flip across the same temperature found recently. Both the L- and S-CRO display an antiferromagnetic ordering at about 150–110 K, with ferromagnetic ordering components at lower temperature. The NTE in S-CRO is a result of a complex interplay among the spin, orbital, and lattice.

PACS: ;65.40.De;;61.66.-f;;71.30.+h;;61.72.Jd;
Keyword:;negative thermal expansion;;structure;;oxygen vacancies;;metal-insulator transition;;octahedra distortion;
1. Introduction

In recent years, the negative thermal expansion (NTE) of materials has received considerable attention due not only to its curious physics and chemistry behind but also to its potential implications for a variety of applications to meet the rapid advances in modern technology.[1–6] To date, the NTE could be driven by several mechanisms: (i) anharmonic phonon vibrations such as in framework oxides,[7–9] ReO3-type fluorides,[10] cyanides,[11,12], etc; (ii) magnetovolume effect such as in Invar alloys and manganese nitrides,[13,14] La(Fe, Si, Co)13,[15,16] and CrAs and Hf1−xTaxFe2 based compounds;[17,18] (iii) ferroelectric transition in PbTiO3 based materials;[19] and (iv) intermetallic charge transfer in SrCu3Fe4O12[20] and BiNiO3.[21] Oxygen vacancies have a profound effect on the magnetic, electronic, and transport properties of transition metal oxide materials and play a vital role in metal–insulating transition (MIT),[22,23] magnetoresistance,[24] catalysis,[25] fuel cells,[26] and supercapacitors.[27] Nevertheless, few studies about the effect of oxygen vacancies on the thermal expansion have been reported.[28,29]

Ca2RuO4 (CRO) is a prototype Mott insulator, where all of the degrees of freedom charge, spin, orbital, and lattice show robust interactions in distinctive phase transitions.[30–34] It undergoes a paramagnetic metal–insulator transition at TMI = 357 K, followed by a well-separated antiferromagnetic order at TN = 110 K.[30,35] The investigation of thermal expansion of CRO can be traced back to Braden et al.[30] and Friedt et al.[31] They observed an increase of lattice volume by 1% upon cooling from room temperature (RT) to 150 K for the stoichiometric crystalline CRO, whereas Alexander et al.[32] reported a strong decrease of lattice volume by 1.3% as the temperature was lowered from 400 K to 70 K for the single crystal CRO. Subsequently, Qi et al. found that M substituting for Ru produces a negative thermal expansion in Ca2Ru1−xMxO4 (M = Cr, Mn, Fe, or Cu).[36,37] Takenaka et al. reported a giant NTE for the reduced ruthenate and attributed it to microstructural effects consuming open spaces in the sintered body on heating.[29] However, the reason for the conflict results in lattice volume thermal expansion reported in crystalline CRO and single crystal CRO remains unclear and the understanding about the intrinsic role of oxygen vacancies played in the thermal expansion property and the MIT of the material is still lacking.

In this paper, we explore the effect of oxygen defects on the intrinsic thermal expansion properties in CRO. For this purpose, we prepared samples with different concentrations of oxygen defects by solid state reactions under different O2/Ar ratios and under ambient atmosphere. It is found that the type of oxygen defects plays a decisive role in the formation of the structure type of CRO, either in a metallic L-CRO or in an insulating S-CRO, and hence affects their temperature dependent behaviors such as structure evolution, thermal expansion, and electrical transportation. Only the S-CRO structure exhibits NTE from 100 K to about 360 K, where it transforms to a high temperature L-CRO phase. However, the two L-CRO phases with different types of oxygen defects are found to be different not only in lattice constant and RuO6 octahedral deformation but also in a series of physical properties. This work provides not only valuable information on the effect of the types of oxygen defects on the structural formation, evolution, and correlated changes in physical properties of CRO, but also a stage for future experimental and theoretical investigations to settle the debating on the nature of the Mott metal--insulator transition based on renewed models taking the oxygen vacancies into account.

2. Experimental details

The CRO samples containing different oxygen contents were prepared by a solid state reaction method with different O2/Ar ratios (0.5%, 1.0%, 1.5%, 2.0%) and in ambient atmosphere conditions. CaCO3 (purity 99%) and RuO2 (purity 99.9%) were used as raw materials which were dried and mixed with 2 : 1 molar ratio. The mixed powders were ground for approximate 2 h and then heated in a furnace at 1643 K for 24 h with a heating and cooling rate of 5 K/min. After cooling naturally, the powders were reground and pressed into cylinders with a diameter of 5 mm under 10 MPa. The cylinders were sintered at 1643 K for 48 h either in ambient atmosphere or in an Ar atmosphere with different percentage of oxygen. To avoid the reaction of the cylinders with the Al2O3 crucible, non-compressed powder of the same composition was used as the bedding powder.

The crystal structure was analyzed by high-resolution synchrotron radiation x-ray diffraction (SXRD, Japan, λ = 0.495724 Å). The powder XRD measurements at different temperatures were also performed with a Bruker D8 Advance x-ray diffractometer with Cu Kα radiation. The software used to analyze the XRD pattern was Fullprof. An AXIS ULTRA x-ray photoelectron spectroscopy (XPS, Shimadzu Kratos) was used to analyze the elemental composition and valence states in the samples. The XPS data analysis was performed by the fractional peak fitting using CasaXPS (v2.3.17).[38] The relative length changes of the bulk samples were measured by a LINSEIS DIL L76 dilatometer at a heating and cooling rate of 5 K/min. Temperature-dependent electrical resistivity and magnetic susceptibility were measured using a Quantum Design physical property measurement system.

3. Results and discussion
3.1. Effect of oxygen contents on the structure formation

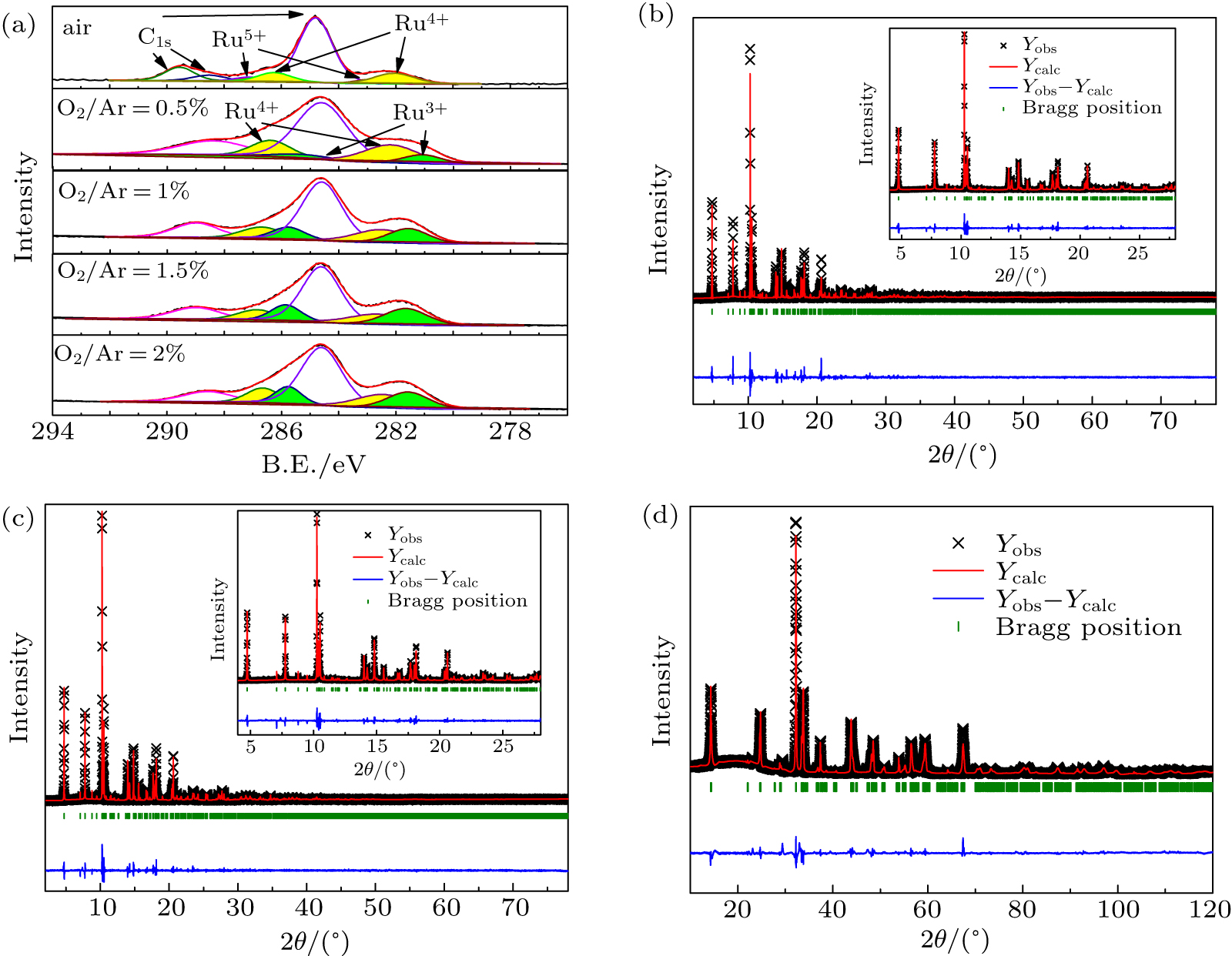
In order to determine the contents of oxygen defects in the samples prepared under different atmospheric conditions, we performed XPS analysis[39] for the Ru 3d orbital binding energies as shown in Fig. 1(a) and compared the results with the NIST XPS database.[40] Figure 1(a) shows clearly that the sample prepared in ambient atmosphere contains minor amount of Ru5+,[41] indicating that Ru4+ is partially oxidized into Ru5+ by excess oxygen, while those prepared under different O2/Ar ratio atmospheric conditions contain certain amount of Ru3+ which increases with the O2/Ar ratio and reaches maximum for the O2/Ar ratio of 1.5%. The obtained binding energies for the Ru 3d5/2 and 3d3/2 orbitals and contents of Ru3+, Ru4+, and Ru5+ in each sample are presented in the supplementary material Table S1. Based on the XPS analysis, the contents of oxygen vacancies are estimated to be about 0.13, 0.23, 0.27, and 0.24 for the samples prepared under O2/Ar ratios of 0.5%, 1.0%, 1.5%, and 2.0%, respectively, while the sample prepared in ambient atmosphere contains an excess oxygen of about 0.09. Therefore, the chemical formulas for these samples might be written as Ca2RuO4.09, Ca2RuO3.87, Ca2RuO3.77, Ca2RuO3.73, and Ca2RuO3.76, respectively.

Fig. 1. (a) XPS analysis for the Ru 4d orbitals of the samples prepared with O2/Ar ratios of 0.5%, 1.0%, 1.5%, and 2.0% and in ambient atmosphere conditions, red: Ru+5, yellow: Ru+4, green: Ru+3. (b)–(d) Rietveld analysis of the SXRD patterns for (b) Ca2RO3.87, (c) Ca2RO3.73 and (d) Ca2RO4.09.

The SXRD analyses for selected samples of Ca2RO4.09, Ca2RO3.87, and Ca2RO3.73 were performed to explore the effect of the oxygen vacancies on the structures as shown in Figs. 1(b)–1(d). All the measured SXRD patterns can be well fitted with an orthorhombic structural model (space group Pbca) but the difference is obvious for the sample containing excess oxygen from the ones with oxygen vacancies. Detailed structural parameters obtained by structure refinements are presented in Table S2. It is shown that the samples with oxygen vacancies adopt the structure of S-CRO with short c-axis at RT while that containing excess oxygen takes the structure of L-CRO with long c-axis.[30,31,33] The 4d4 layered perovskite CRO is made of planes of corner-sharing RuO6 octahedra separated by Ca atoms.[30,42] The structure is distorted by a rotation of the oxygen octahedra about the c axis and a tilt about an in-plane axis. Compared to the L-CRO, the S-CRO has a shorter c-axis, longer a- and b-axes, and a larger cell volume. The enlargement of the a and b axes by the introduction of oxygen vacancies is due to the expansion of the Ru–O(1)–Ru angle and the rotation angle of the Ru–O(2) bonds about the c-axis, instead of the volume change of the RuO6 octahedra (see Table S2), because both give rise to a larger projection in the ab-plane while the latter contributes to a smaller c-axis. For the sample with excess oxygen, the octahedra are strongly elongated along the long axis with a reduced rotation and tilt angles which account for the larger long axis.

The above observations demonstrate that it is the oxygen content that governs the crystallization of CRO either in the S-Pbca or the L-Pbca phase, i.e., the types of oxygen defects play a vital role in the structure formation. It explains why the samples synthesized at different temperatures crystallized in different phases and the L-CRO phase could be obtained by annealing the powders of the S-CRO phase at 673 K for 50 h,[43] though the authors claimed the oxygen content of 4.0 per formula in both samples. In fact, the formation of the S-CRO or L-CRO phase could be very sensitive to the types of oxygen defects, even the contents could not be detected.

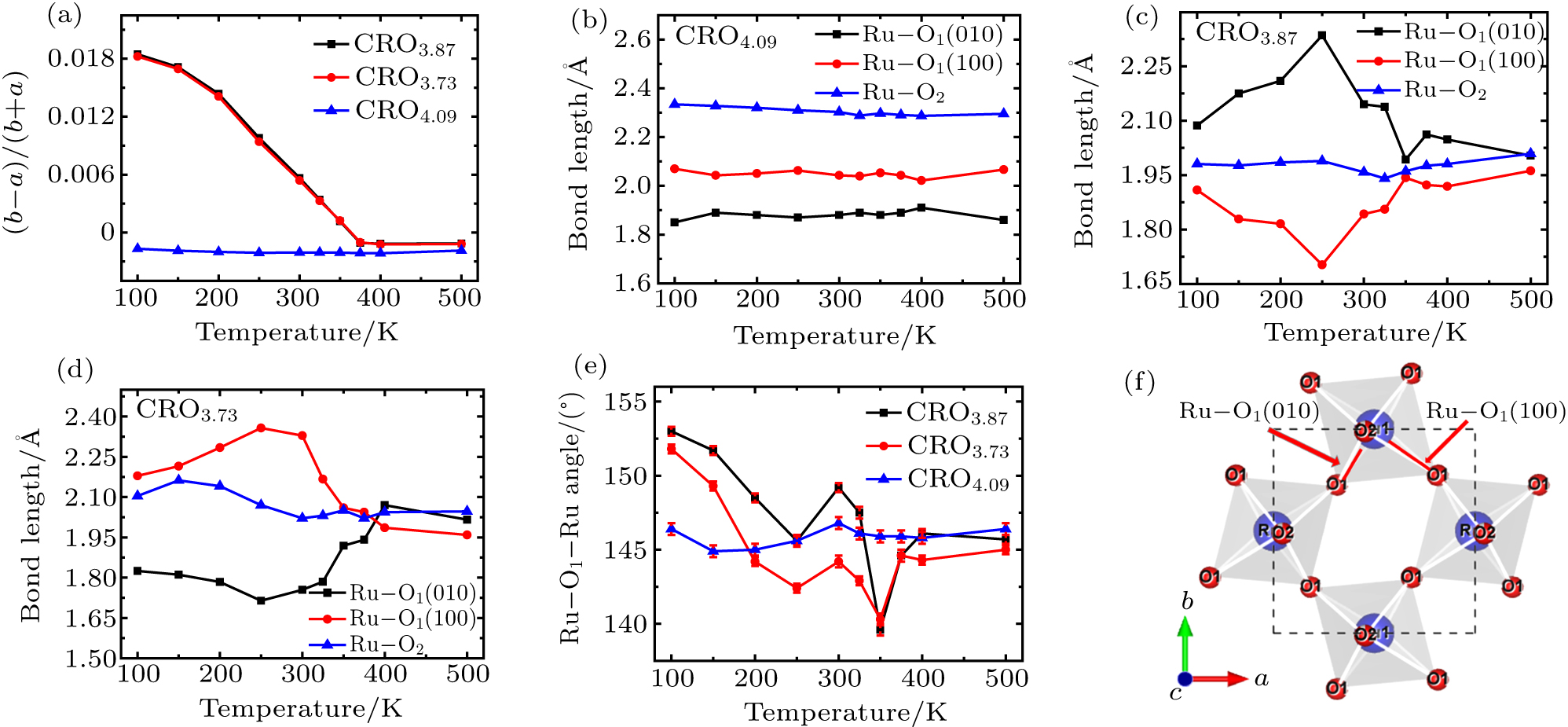
3.2. Effect of oxygen contents on the thermal expansion property

Though the samples with oxygen vacancies have a smaller c axis, but they have a larger lattice volume with respect to that containing excess oxygen. A large cell volume favors the appearance of NTE since it enhances the flexibility for the polyhedra movement. We show in Fig. 2(a) the relative length changes of the samples synthesized under different atmospheric conditions. The results show that all the samples with oxygen vacancies exhibit enormous NTE from 100 K to about 360 K and the largest NTE is observed for the sample of Ca2RuO3.73 which contains the most oxygen vacancies. The turning points in the thermal expansion curves comply with the MIT temperature.[30] The linear coefficients of thermal expansion (CTE) for the samples prepared under different O2/Ar ratios are α4.09 = 11.5 ppm/K (T < 500 K), α3.87 = −62.9 ppm/K, α3.77 = −65.8 ppm/K, α3.76 = −68.3 ppm/K, α3.73 = −94.4 ppm/K (T < 355 K, the subscript denotes the oxygen content per formula). The NTE approximately increases with the content of oxygen vacancies. By contrast, the sample containing excess oxygen displays a normal thermal expansion behavior. A giant NTE for the reduced layered ruthenate was also observed by Takenaka et al. who attributed it to microstructural effects.[29] In the following, we concentrate on the effect of oxygen vacancies on the intrinsic nature of lattice thermal expansion and crystal structure evolution.

Fig. 2. Thermal expansion property: (a) relative length change of ceramic cylinders measured by dilatometry; (b)–(e) changes of lattice constants, lattice volume, and (f) the Ca–Ru distance for (b) Ca2RuO4.09, (c) Ca2RuO3.87, and (d) Ca2RuO3.73 with temperature. The insert shows the octahedron rotation about the c-axis and tilt about an axis in the Ru–O(1) plane.

In order to see the effect of oxygen vacancies on the intrinsic thermal expansion properties, we carried out XRD measurements for the samples of Ca2RuO4.09, Ca2RuO3.87, and Ca2RuO3.73 from 100 K to 500 K and obtained the structure parameters by Rietveld refinements. Typical data at selected temperatures are presented in Table S3. Figures 2(b)–2(e) show the calculated axial and lattice volume changes with temperature. For the sample containing excess oxygen, all three axes display a continuous increase upon heating from 100 K to 500 K (Fig. 2(b)), resulting in a normal thermal expansion in lattice volume (Fig. 2(e)), whereas for the samples with oxygen vacancies, only the a and c axes show an increase and the b axis shrinks markedly till about the phase transition temperature (Figs. 2(c) and 2(d)), leading to an NTE in lattice volume from 150 K to about the MIT temperature (Fig. 2(e)). The axial and lattice volume CTEs are calculated and listed in Table 1. These results demonstrate that the thermal expansion properties of CRO are very sensitive to the stoichiometric content of oxygen, particularly the types of oxygen defects, and the intrinsic NTE appears only in the samples with oxygen vacancies. This explains why the conflict results in the so-called stoichiometric polycrystalline CRO and single crystal CRO were observed by different groups.[30,33] The different thermal expansion properties in L-CRO and S-CRO are also manifested by the changes of the in-plane bond length or Ru–O(1)–Ru distance with temperature as shown in Fig. S1.

Table 1.

Coefficients of axial and lattice volume expansion.

.

The a and b axes shrink concomitantly for the sample containing excess oxygen upon cooling (Fig. 2(b)), whereas the b axis exhibits a marked elongation accompanied by a moderate shrinkage of the a axis for the samples with oxygen vacancies (Figs. 2(c) and 2(d)), indicating an increasingly strong orthorhombic distortion in the Ru–O(1) plane. In Fig. 3(a) we show how the orthorhombic strain, which is defined as ε = (b − a) / (b + a), develops with temperature. It is shown that the orthorhombic strain is very small and shows little changes upon cooling in the sample containing excess oxygen, whereas it increases rapidly below the structural transformation temperature in the samples with oxygen vacancies. The enhancement of the orthorhombic strain upon cooling reflects an increasingly large in-plane distortion arising from the changes of the Ru–O(1) bonds and Ru–O(1)–Ru bond angles.

Fig. 3. (a)–(c) Temperature dependent changes of (a) orthorhombic strain, (b)–(d) Ru–O(1) bond lengths in (010) and (100) directions, and Ru–O(2) bond length of Ca2RuO4.09, Ca2RuO3.87, and Ca2RuO3.73, (f) RuO6 octahedra.

In order to get insight into the effect of the octahedral distortion on the thermal expansion properties, we depict in Figs. 3(b)–3(e) the changes of the Ru–O(1) and Ru–O(2) bond lengths and bond angles with temperature. Compared to the sample containing excess oxygen which exhibits a relatively smooth change in both bond lengths and bond angles upon cooling (Fig. 3(b)), the samples with oxygen vacancies present a quite different scenario. The Ru–O(1) bond lengths along the (010) and the (100) directions display huge but opposite changes upon cooling and the largest difference is reached across about 250 K, an indication of the largest in-plane distortion of the octahedra, while the out of plane Ru–O(2) bonds change moderately (Figs. 3(c), 3(d), and 3(f))). It is worth noting that the difference of the Ru–O(1) bond lengths in orthogonal directions becomes progressively smaller accompanied by a continuous increase of the Ru–O(1)–Ru bond angle below about 250 K (Fig. 3(e)), above which the changes seem irregular, however. We show in Fig. S2 the octahedral distortions for Ca2RuO4.09, Ca2RuO3.87, and Ca2RuO3.73 at 300 K, 250 K, and 100 K, respectively. The largest distortion for the oxygen deficient samples shows up at about 250 K.

It is noted that an antiferromagnetic orbital ordering even in the paramagnetic phase below TOO = 260 K was suggested from resonant x-ray scattering experiments[44,45] and a strong suppression of oscillation-amplitude for an Ag symmetric phonon mode and a phase flip over 180° across the same temperature were observed by a recent optical pump–probe experiment.[46] We believe that the Ru–O(1) bond length and bond angle changes observed in Figs. 3(c)–3(e) across about 250 K should be closely correlated to the formation of the antiferromagnetic orbital ordering in the paramagnetic phase and the Ag mode suppression and phase flip since the Ag mode can be described as the octahedral tilting associated with motions of both in-plane oxygen (O1) and apical oxygen (O2). Density functional theory calculations suggested that the Ag mode oscillations result in x/y-anisotropic octahedral distortions.[47] The Raman susceptibility may change sign across the bond length maximum/minimum and consequently lead to the Ag mode suppression and phase flip. An increase in bond angle may facilitate superexchange interaction and favor the antiferromagnetic orbital ordering. Therefore, the evolution of the RuO6 octahedra distortion upon cooling observed here may provide a direct structural evidence for the antiferromagnetic orbital ordering in the paramagnetic phase and the Ag mode suppression and phase flip across the critical temperature TOO = 260 K.

The excess oxygen in the interstitials will oversaturate the Ca coordination and lead to a charge transfer towards the RuO2 planes which requires oxidation of Ru higher than 4+ as evidenced by the XPS analysis. It consequently results in smaller Ru–O(1) and larger Ru–O(2) equilibrium distances and a relaxation of the strain implied by the misfit of smaller radius of Ca in the structure. At the same time, it also modulates the orbital polarization and the interlayer van der Waals interactions. As a result, it leads to the crystallization of the L-CaRO phase at RT with longer c axis and shorter a and b axes with respect to the counterparts of the S-CRO phase with oxygen deficiencies (a: 5.3112 Å vs. 5.4070 Å, b: 5.2990 Å vs. 5.4685 Å, c: 12.3770 Å vs. 11.9842 Å). The inserted oxygen atoms play a decisive role in the formation of the L-Pbca structure with lower orthorhombic strain at RT and in retaining the structure over a wide temperature range.

By contrast, an oxygen vacancy plays the role of double electron donors which requires the reduction of Ru lower than 4+ as revealed by the XPS analysis and results in a shorter Ru–O(2) equilibrium distance and a larger Ru–O(1) equilibrium bond length difference, making the RuO6 octahedra more distorted and flattened. It leads to the formation of S-CRO phase with much higher orthorhombic strain than that in the case with additional interstitial oxygen atoms. The expanding of the b axis in the S-CRO upon cooling is responsible for the lattice volume NTE, which is a complex interplay between the Ru–O(1) bond length and bond angle as well as the RuO6 octahedral rotation and tilting. However, the NTE mechanisms below and above 260 K may be not completely the same as indicated by the distinct changes of octahedral distortion across the temperature. The formation of the antiferromagnetic orbital ordering in the paramagnetic phase may make a contribution to the NTE below 260 K since the paramagnetic to antiferromagnetic phase transition is also accompanied by a volume expansion in Mn3AN upon cooling.[13,14]

Besides the enormous NTE, the samples with oxygen vacancies are also characterized by a distinct structure transition from the low-temperature orthorhombic S-CRO to a high-temperature L-CRO phase as indicated by the marked increase in the c axis around 350 K (Figs. 2(c) and 2(d)).[32] The phase transition may be understood by the release of the orthorhombic strain with increasing temperature, namely, it is a structure driving phase transition. The c-axis elongation in the oxygen deficient samples tracks the trend of the Ru–O(2)–Ca distance with the increase of temperature (Fig. 2(f)), suggesting that it is mainly caused by the increment of the Ru–O(2) bond length or the Ru–O(2)–Ca distance. It is worth noting that there are distinctive differences between the two L-CRO phases, the one containing excess oxygen (L-CRO4+δ) and the one transformed from the S-CRO with oxygen vacancies (L-CRO4−δ): (a) the structural transition in L-CRO4−δ is reversible while no structure transition occurs in L-CRO4+δ; (b) with respect to L-CRO4+δ, L-CRO4−δ has an obviously larger lattice volume (352.66 Å3 vs. 349.42 Å3, at 400 K) but shorter Ru–O(2) bond length (2.044 Å vs. 2.287 Å); (c) the Ru–O(2) rotation and Ru–O(1) tilt angles of the RuO6 octahedra in L-CRO4–δ are obviously smaller. It is these distinctions that make them utterly different in thermal expansion and phase transition characters as well as other physical properties as can be seen below.

3.3. Effect of oxygen content on the electric and magnetic properties

Figure 4(a) shows the temperature dependence of electrical resistivity for Ca2RuO3.87, Ca2RuO3.73, and Ca2RuO4.09. While the sample containing excess oxygen retains the metallic behavior in the whole temperature range measured, those with oxygen vacancies exhibit a metal–insulator transition but the onset of insulating behavior is not as clear as the structure transition probably due to that the ceramic samples are not densely packed. The origin of the MIT has been the topic of hot debating. Different scenarios have been suggested, such as an orbital-selective Mott transition,[48] a crystal-field splitting assisted single Mott transition,[49] and Coulomb-enhanced spin–orbit interaction induced transition.[50] Recent local-density approximation + dynamical mean-field theory calculations suggest that the Mott metal–insulator transition is mainly driven by the change in structure from long to short c-axis layered perovskite instead of the spin–orbit interaction, and the spin–orbit coupling, magnetic ordering, and anisotropic Coulombic interactions are not decisive.[34,51] As discussed in the last section, our results present a clue of structure driving phase transition by releasing of the orthorhombic strain upon heating in the oxygen deficient samples. The presence of oxygen vacancies regionalizes electron spin in Ru 4d, hindering electron transport and thus increasing the resistivity.[24,53]

Fig. 4. (a) Temperature dependence of (a) resistivity and (b) the field-cooled and zero-field-cooled susceptibility of Ca2RuO3.87, Ca2RuO3.73, and Ca2RuO4.09. Insertion: the magnetization curves at T = 10 K.

In Fig. 4(b) we present the field-cooled and zero-field-cooled susceptibilities for the samples. Both the samples with excess oxygen and oxygen vacancies display antiferromagnetic ordering below 150–110 K. A significant magnetic hysteresis presented in the magnetization curves manifests that the magnetic structure has a ferromagnetic component.[41] The magnitude of the remanent magnetic moment estimated from the M–H curve is about 0.5 emu per gram of Rum+ (m = 3,4). The antiferromagnetic ordering is dominated by the in-plane superexchange interactions between neighboring Ru’s, which will sensitively depend on both bond lengths and bond angles.[30] A shorter bond length and a larger bond angle seem to enhance the interaction. The presence of oxygen vacancies reduces Ru4+ partially to Ru3+ which makes the Ru 4d orbital become half full and changes the overlapping and hybridization degree between Ru 4d and O 2p orbitals, leading to the weakening of the coupling strength between Rum+ (m = 3, 4) and O 2p spin orbitals.

4. Conclusions

The types of oxygen defects play a decisive role in the formation of structure type in Ca2RuO4 and hence affect a series of their physical properties. The sample containing excess oxygen adopts the metallic L-CRO structure, whereas those with oxygen vacancies take the insulating S-CRO phase at RT. While the L-CRO structure containing excess oxygen displays a normal thermal expansion property without structure transformation from 100 K to 500 K, the S-CRO structure exhibits enormous NTE from 100 K to about 360 K, where it transforms to a high temperature metallic L-CRO phase which differs from its counterpart with excess oxygen in lattice parameters, RuO6 octahedral deformation, and a series of physical properties. Compared to the L-CRO with excess oxygen, the S-CRO has a distinctively larger in-plane RuO6 octahedral distortion which reaches the maximum across about 260 K and then relaxes monotonically as indicated by the progressive reduction of the in-plane bond length difference and extension of the bond angle. This might be taken as a structural evidence for the antiferromagnetic orbital ordering in the paramagnetic phase and the Ag mode suppression and phase flip found recently. All the samples display antiferromagnetic ordering at about 150–110 K, below which a ferromagnetic orbital ordering component appears in the antiferromagnetic phase. The NTE in S-CRO arises from a complex interplay among the spin, orbital, and lattice. In addition to the knowledge presented, this work might set up an stage for future experimental and theoretical investigations to settle the debating on the nature of Mott metal–insulator transition by taking oxygen vacancies in to account and prompt the exploring of NTE materials along the line of oxygen vacancies.

Reference
[1] Mary T A Evans J S O Vogt T Sleight A 1996 Science 272 90
[2] Chen J Hu L Deng J X Xing X R 2015 Chem. Soc. Rev. 44 3522
[3] Mittal R Gupta M K Chaplot S L 2018 Prog. Mater. Sci. 92 360
[4] Belo J H Pires A L Gomes I T Sousa J B Hadimani R L Jiles D C Ren Y Zhang X Y Araujo J P Pereira A M 2019 Phys. Rev. 100 134303
[5] Tong P Wang B S Sun Y P 2013 Chin. Phys. 22 067501
[6] Ge X H Mao Y C Li L Li L P Yuan N Cheng Y G Guo J Chao M J Liang E J 2016 Chin. Phys. Lett. 33 046503
[7] Ge X H Mao Y C Liu X S Cheng Y G Yuan Y L Chao M J Liang E J 2016 Sci. Rep. 6 24832
[8] Song W B Liang E J Liu X S Li Z Y Yuan B H Wang J Q 2013 Chin. Phys. Lett. 30 126502
[9] Chen D X Zhang Y Ge X H Cheng Y G Liu Y Y Yuan H L Guo J Chao M J Liang E J 2018 Phys. Chem. Chem. Phys. 20 20160
[10] Li C W Tang X Munoz J A Keith J B Tracy S J Abernathy D L Fultz B 2011 Phys. Rev. Lett. 107 195504
[11] Cairns A B Catafesta J Levelut C Rouquette J Lee A Peters L Thompson A L Dmitriev V Haines J Goodwin A L 2013 Nat. Mater. 12 212
[12] Ding P Liang E J Jia Y Du Z Y 2008 J. Phys.: Condens. Matter. 20 275224
[13] Takenaka K Takagi H 2005 Appl. Phys. Lett. 87 261902
[14] Shi K W Sun Y Yan J Deng S H Wang L Wu H Hu P W Lu H Q Malik M I Huang Q Z Wang C 2016 Adv. Mater. 28 3761
[15] Huang R J Liu Y Y Fan W Tan J Xiao F R Qian L H Li L F 2013 J. Am. Chem. Soc. 135 11469
[16] Li W Huang R Wang W Tan J Zhao Y Q Li S P Huang C J Shen J Li L F 2014 Inorg. Chem. 53 5869
[17] Hu Y Zheng X Q Ma G D Lu H Q Zhang L Zhang C S Xia Y H Hao Y Q He L H Chen J Shen F R Wang S G Wang C Wang D H Du Y W 2019 Phys. Rev. Appl. 12 034027
[18] Li L F Tong P Zou Y M Tong W Jiang W B Jiang Y Zhang X K Lin J C Wang M Yang C Zhu X B Song W H Sun Y P 2018 Acta Mater. 161 258
[19] Pan Z Chen J Jiang X X Hu L Yu R Z Yamamoto H Ogata T Hattori Y Guo F M Fan X A Li Y W Li G Q Gu H Z Ren Y Lin Z S Azuma M Xing X R 2017 J. Am. Chem. Soc. 139 14865
[20] Long Y W Hayashi N Saito T Azuma M Muranaka S Shimakawa Y 2009 Nature 458 60
[21] Azuma M Chen W T Seki H Czapski M Olga S Oka K Mizumaki M Watanuki T Ishimatsu N Kawamura N Ishiwata S Tucker M G Shimakawa Y Attfield J P 2011 Nat. Commun. 2 347
[22] Jeong J Aetukuri N Graf T Schladt T D Samant M G Parkin S S P 2013 Science 339 1402
[23] Lee D Chung B Shi Y Kim G Y Campbell N Xue F Song K Choi S Y Podkaminer J P Kim T H Ryan P J Kim J W Paudel T R Kang J H Spinuzzi J W Tenne D A Tsymbal E Y Rzchowski M S Chen L Q Lee J Eom C B 2018 Science 362 1037
[24] Dash U Acharya S K Lee B W Jung C U 2017 Nanoscale Res. Lett. 12 168
[25] Campbell C T Peden C H F 2005 Science 309 713
[26] Liu G H Li J D Fu J Jiang G P Lui G Luo D Deng Y P Zhang J Cano Z P Yu A Su D Bai Z Y Yang L Chen Z W 2019 Adv. Mater. 31 1806761
[27] Kim H S Cook J B Lin H Ko J S Tolbert S H Ozolins V Dunn B 2017 Nat. Mater. 16 454
[28] Cheng Y G Mao Y C Yuan B H Ge X H Guo J Chao M J Liang E J 2017 Phys. Lett. 381 2195
[29] Takenaka K Okamoto Y Shinoda T Katayama N Sakai Y 2017 Nat. Commun. 8 14102
[30] Braden M Andre G Nakatsuji S Maeno Y 1998 Phys. Rev. 58 847
[31] Friedt O Braden M Andre G Adelmann P Nakatsuji S Maeno Y 2001 Phys. Rev. 63 174432
[32] Alexander C S Cao G Dobrosavljevic V McCall S Crow J E Lochner E Guertin R P 1999 Phys. Rev. 60 R8422
[33] Jain A Krautloher M Porras J Ryu G H Chen D P Abernathy D L Park J T Ivanov A Chaloupka J Khaliullin G Keimer B Kim B J 2017 Nat. Phys. 13 633
[34] Zhang G R Pavarini E 2017 Phys. Rev. 95 075145
[35] Cao G McCall S C Crow J E Guertin R P 1997 Phys. Rev. 56 5387
[36] Qi T F Korneta O B Parkin S De Long L E Schlottmann P Cao G 2010 Phys. Rev. Lett. 105 177203
[37] Qi T F Korneta O B Parkin S Hu J P Cao G 2012 Phys. Rev. 85 165143
[38] Shirley D A 1972 Phys. Rev. 5 4709
[39] Morgan D J 2015 Surf. Interface Anal. 47 1072
[40] Rumble J R Bickham D M Powell C J 1992 Surf. Interface Anal. 19 241
[41] Lü M F Deng X Waerenborgh J C Wu X J Meng J 2012 Dalton T. 41 11507
[42] Dabrowski B Chmaissem O Klamut P W Kolesnik S Maxwell M Mais J Ito Y Armstrong B D Jorgensen J D Short S 2004 Phys. Rev. 70 014423
[43] Nakatsuji S Ikeda S Maeno Y 1997 Physica 282�?87 729
[44] Zegkinoglou I Strempfer J Nelson C S Hill J P Chakhalian J Bernhard C Lang J C Srajer G Fukazawa H Nakatsuji S Maeno Y Keimer B 2005 Phys. Rev. Lett. 95 136401
[45] Porter D G Granata V Forte F Matteo S D Cuoco M Fittipaldi R Vecchione A Bombardi A 2018 Phys. Rev. 98 125142
[46] Lee M C Kim C H Kwak I Kim J Yoon S Park B C Lee B Nakamura F Sow C Maeno Y Noh T W Kim K W 2018 Phys. Rev. 98 161115
[47] Lee M C Kim C H Kwak I Seo C W Sohn C H Nakamura F Sow C Maeno Y Kim E A Noh T W Kim K W 2019 Phys. Rev. 99 144306
[48] Anisimov V I Nekrasov I A Kondakov D E Rice T M Sigrist M 2002 Eur. Phys. J. 25 191
[49] Pavarini E Yamasaki A Nuss J Andersen O K 2005 New J. Phys. 7 188
[50] Liu G Q 2011 Phys. Rev. 84 235136
[51] Gorelov E Karolak M Wehling T O Lechermann F Lichtenstein A I Pavarini E 2010 Phys. Rev. Lett. 104 226401
[53] Zhang Q Xu Z F Wang L F Gao S Yuan S J 2015 J. Alloy. Compd. 649 1151