† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474116 and 11674118).
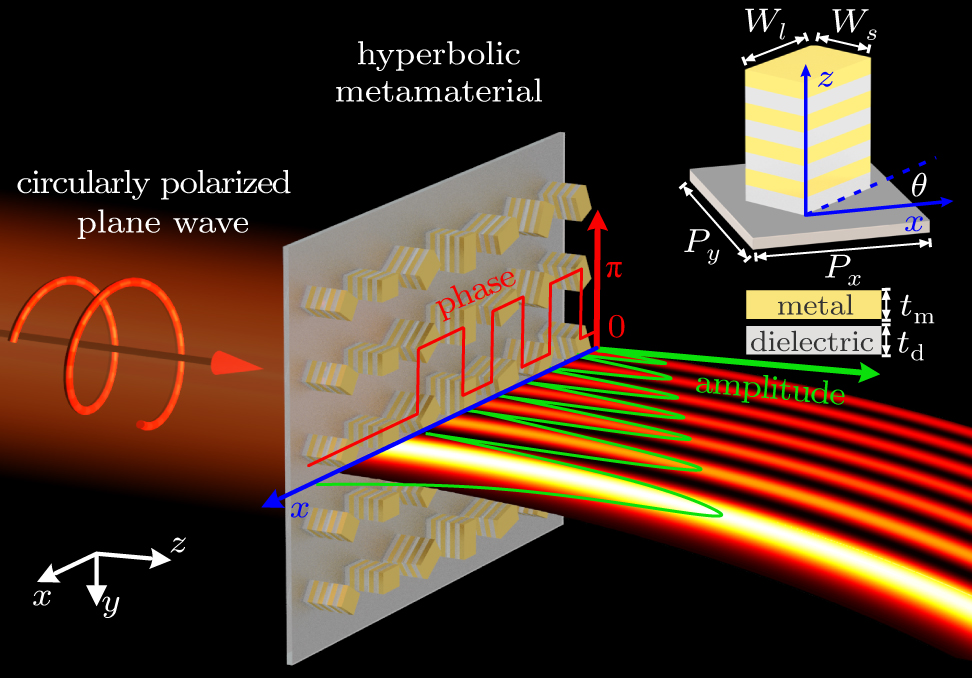
Metasurfaces have exhibited considerable capability for generating Airy beams. However, the available plasmonic/dielectric metasurfaces Airy-beam generators have low transmission efficiency and/or poor quality of generated beam because they lack the amplitude modulation. Hyperbolic metamaterials (HMMs) have recently provided an alternative strategy for building high-performance meta-devices that are capable of flexibly modulating the phase, amplitude and polarization state of light. Here we reveal that both the propagation phase and the Pancharatnam–Berry phase can contribute to the local transmission phase of circularly polarized electromagnetic waves by using HMMs. This thus provides us with great freedom to design HMM units with different cross-sections to independently control the transmission phase and amplitude. Here, we design circularly polarized Airy-beam generators in the microwave and near-infrared domains, which require binary phase and polynary amplitude, and validate the good performance in the microwave experiment. Our work can facilate the generation of a complicated light field that highly requires independent and complete control of the transmission phase and amplitude under circularly polarized incidence.
As a kind of diffraction-free beams, Airy beams have attracted much attention due to their intriguing self-bending, diffraction-free, and self-healing properties.[1–4] By making use of these unique properties, numerical potential applications have been explored, including light-sheet microscopy,[5,6] optical nano/micromanipulation,[4] optical trapping,[7] optical steering,[8] and curved plasma generation.[9] Customary approaches to generate Airy beams usually require very bulky and complex optical systems, including a spatial light modulator and a Fourier transform lens,[3,4] which is against high-density photonic integration.
Metasurfaces, the two-dimensional version of metamaterials, have served as an innovative platform for manipulating the properties of electromagnetic (EM) waves by locally modulating the phase, amplitude, and/or polarization state of the scattered field in a subwavelength scale.[10–17] Inspired by the flexibility of locally controlling the phase and amplitude of light, metasurfaces have been broadly employed to generate Airy beams for both surface waves at the chip level[18–23] and free-space light.[23–30] The Airy beams for surface waves are revealed with plasmonic metasurfaces.[18–23] For generating the Airy beams for free-space light, both of plasmonic and dielectric metasurfaces are used either for linearly or circularly polarized light incidence.[23–30] However, the Airy beams with plasmonic metasurfaces still face the issue of low transmission efficiency which is defined as the ratio of the maximum electric field intensity of the Airy beams to the intensity of the incident plane waves,[29,31,32] due to the intrinsically low conversion efficiency for plasmonic meta-atoms.[23–29] The Airy beams with dielectric metasurfaces can address the issue of low transmission efficiency, but they typically have a poor quality due to the lack of amplitude modulation.[30] Quite recently, a novel approach for constructing transmissive metasurfaces, with high working efficiencies (the total transmission/incidence ratio) and broad working bands has been established with hyperbolic metamaterials (HMMs).[32–35] HMMs can support a branch of surface waves (SWs) on their lateral walls, and they use SWs propagation inside the HMMs to manipulate the transmission phase and amplitude. HMMs have been demonstrated to be capable of molding the wave-front of the transmitted EM waves in nearly arbitrary ways, leading to a variety of applications such as focusing lenses,[33] polarization manipulation,[34,35] and Airy beam generation for linearly polarized EM waves.[32]
In this paper, it is shown that the local transmission phase of circularly polarized EM waves is associated with both the propagation phase and the Pancharatnam–Berry (PB) phase. The local transmission amplitude of circularly polarized EM waves through the HMM is highly dependent on its cross-sections. Meanwhile, we can always make the local transmission phase reach the pre-designed value by modulating the orientation angle to realize particular wave-manipulation applications. As a demonstration of strategies for obtaining a complex EM field, we have designed and fabricated a microwave Airy beam generator, which demonstrated good performance in experiment.
Figure
Considering the modal birefringence of an RHMM unit, we can denote the complex transmission coefficients for l- and s-polarization incidences as
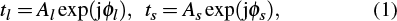
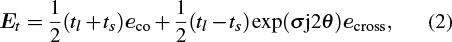

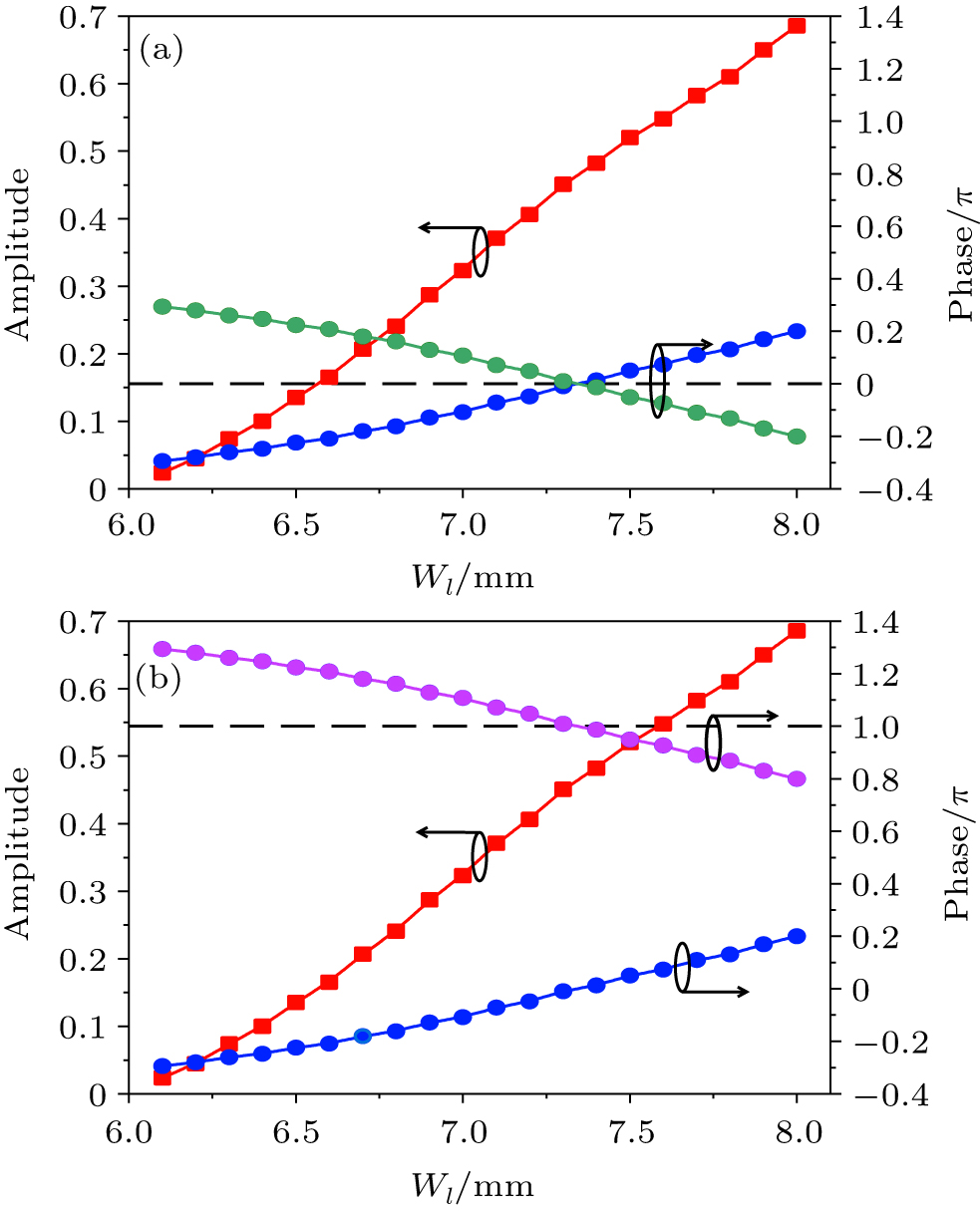
Using the finite difference time domain (FDTD) method of the commercial software Lumerical FDTD Solutions, we simulated the EM responses of the RHMM arrays. It is emphasized here that both of the LCP and RCP incidences can be used to design the Airy beam generator, we have merely taken the LCP incidence as an example. In this case, both of the LCP and RCP components exist in the output space, but the device’s geometrical parameters have been designed to enable the phase and amplitude distributions of the RCP component to follow the Airy envelope. The transmission amplitude and propagation phase of the RCP component vary with Wl (from 6 mm to 8 mm) under LCP incidences at 8.6 GHz, as respectively shown with red squares and blue dots in Fig.

For the generation of the Airy beam, the transmitted EM waves of an HMM Airy beam generator should satisfy the initial envelope of the Airy beam. For a finite energy 1D Airy beam its electric field distribution satisfies[3]

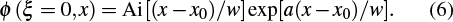
For the generation of the 1D Airy beam, we can arrange the RHMM meta-atoms with various lengths of cross-sectional long-edges and orientation angles along the x direction to enable Et,cross to satisfy the initial Airy envelope, while keeping the y direction periodic (shown in Fig.
In the design, the LCP component always co-exists in the output space, but its electric field is always orthogonal to that of the RCP component. Consequently, it does not affect the generated field distributions of the Airy beam that is formed by the RCP component. We performed FDTD simulations to model the EM response of the HMM Airy beam generator and verified the generation of the Airy beam with sample fabrication and measurement. A part of the sample is shown in Fig.

 | Fig. 5. The measured electric field intensity distributions of the transmitted RCP around the pre-design frequency of 8.6 GHz: (a) 8.4 GHz, (b) 8.5 GHz, (c) 8.7 GHz, and (d) 8.8 GHz. |
The design method of a circularly polarized Airy beam generator can also be employed in terahertz and optical frequency domains so long as the proper metal and dielectric materials are used to construct the HMM meta-atoms. Here, we chose to demonstrate a circularly polarized HMM Airy beam generator at 1.55 μm. The RHMM meta-atom, consisting of a silver/silica multilayer, is assumed to deposit on a silica substrate.[38] The thicknesses for each silver and silica layer are tm = td = 40 nm, and ten pairs of silver/silica layers are used to construct the RHMM meta-atom. The lattice constants along the x- and y-directions are P = Px = Py = 600 nm. The RHMM units have a long-edge width varying from 265 nm to 355 nm and a constant short-edge width of 260 nm. The amplitude and propagation phase of the transmitted RCP electric field under LCP incidence are shown in Fig.
To summarize, we have put forward a general design strategy for constructing high-efficiency circularly polarized Airy beam generators. In contrast to customary metasurface Airy beam generation strategies, both the propagation phase and PB phase can be used to tune the local transmission phase of circularly polarized EM waves with HMMs. This allows us to independently control the transmission phase and amplitude by changing the cross-section of the HMM unit and its orientation angle to fully satisfy the binary phase and polynary amplitude distributions required by Airy beams. A proof-of-concept experiment was implemented to demonstrate the generation of Airy beams with HMMs under LCP incidence in the microwave regime. This design strategy can also be employed for terahertz and near-infrared waves by scaling down the geometry. The presented results pave a promising avenue for constructing complex photonic devices that require independent and complete control of the transmission amplitude and phase under circularly polarized incidence.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |