† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11674268 and 11764038), the Natural Science Foundation of Guangdong Province, China (Grant No. 2020A1515010927), and Department of Education of Guangdong Province, China (Grant Nos. 2018KCXTD011 and 2019KTSCX037).
We present the recent new developments of time-dependent Schrödinger equation and time-dependent density-functional theory for accurate and efficient treatment of the electronic structure and time-dependent quantum dynamics of many-electron atomic and molecular systems in intense laser fields. We extend time-dependent generalized pseudospectral (TDGPS) numerical method developed for time-dependent wave equations in multielectron systems. The TDGPS method allows us to obtain highly accurate time-dependent wave functions with the use of only a modest number of spatial grid point for complex quantum dynamical calculations. The usefulness of these procedures is illustrated by a few case studies of atomic and molecular processes of current interests in intense laser fields, including multiphoton ionization, above-threshold ionization, high-order harmonic generation, attosecond pulse generation, and quantum dynamical processes related to multielectron effects. We conclude this paper with some open questions and perspectives of multiphoton quantum dynamics of many-electron atomic and molecular systems in intense laser fields.
The fundamental phenomena from a laser beam focused on a atomic or molecular target, such as multiphoton ionization (MPI), above-threshold ionization (ATI), high-order harmonic generation (HHG), attosecond pulses generation (APG), etc., have been largely studied over the last decade. Driven by the experimental works, theoretical non-perturbative methods and various models have been proposed for the atomic and molecular dynamical behaviors in intense laser fields. The semiclassical three-step model developed by Corkum[1] and Kulander[2] has shown a fairly clear physical picture of laser-driven electronic rescattering and has been successfully extended to include some quantum effects.[3] However, with rapidly developing laser techniques, a number of very-high-order nonlinear optical processes, such as many-electron correlation effects, non-sequential double ionization, etc., have been observed from many-electron systems in intense laser pulses.[4] To study such strong nonlinear optical phenomena observed in many-electron systems, a quantitative description of the dynamics of the system will be most reliably obtained from integration of the full-dimensional time-dependent Schrödinger equation (TDSE) based on the full many-body Hamiltonian.
For the simplest many-electron system, such as helium atom with two electrons, theoretical description of this process is a six-dimensional numerical integration of the TDSE, several approaches have been proposed.[5,6] However, fully converged N-electron systems (N > 2) calculation with 3N-dimensional TDSE is still difficult to achieve and remains a major computational challenge in the study of strong-field atomic, molecular, and optical physics today. One of the approximations commonly used for the treatment of strong-field processes in the past decade is the single-active-electron (SAE) model with frozen nuclei.[7] The SAE approach is a theoretical model frequently employed to investigate scenarios in which inner-shell electrons may productively be treated as frozen spectators to a physical process of interest, providing useful insights regarding strong-field systems dynamics. However, within the SAE approach, the effects of many-electron correlation and the individual spin–orbital contribution can not be explicitly treated.
In current frontiers of laser sciences, studies of interactions between a highly-intense, ultrashort laser pulse and many-electron systems have been attracting much attention. It is desirable to explore more comprehensive formalisms for detailed treatment of strong-field processes, taking into account both the electron correlation and the structure of the excited states, and at the same time allowing for the core excitation of the many-electron systems. Density functional theory (DFT) provides a first-principles approach for the quantum-mechanical description of electrons and bypasses the need for direct calculation of a many-electron wavefunction, which is based on the earlier fundamental work of Hohenberg and Kohn[8] and Kohn and Sham.[9] It is one of the most widely used methods for ab initio calculations of the structure of atoms, molecules, and crystals.[10–14] In Kohn–Sham DFT formalism, 3N-dimensional numerical integration problem is decomposed into a set of orbitals by the electron density, leading to a set of one-electron Schrödinger-like equations to be solved self-consistently. The Kohn–Sham equations are structurally similar to the Hartree–Fock equations but include in principle exactly the many-body effects through a local exchange–correlation (xc) potential. Thus DFT is computationally much less expensive than the traditional ab initio many-electron wavefunction approaches and this accounts for its great success for large systems.[15,16]
The central theme of DFT is possible and beneficial to obtain the xc-energy functional for electronic systems, its formally exact expression is unknown. The xc-energy functional can be approximated by the local density approximation (LSDA)[17] or the generalized gradient approximation (GGA).[18–21] Such approximations are widely and successfully used to predict, understand, and design physical and chemical phenomena associated with molecules and materials. However, the xc potentials derived from these GGA energy functionals suffer similar problems as in LSDA and do not exhibit the asymptotically correct long-range Coulombic tail –1/r behavior that is expected from general considerations. The problem of the incorrect long-range behavior of the LSDA and GGA energy functionals is so-called self-interaction error (SIE).[22] Thus, whereas widely used GGA approximations allow for rather accurate predictions of the total energies of the ground states of atoms and molecules, but the excited-state energies and the ionization potentials obtained from the highest occupied orbital energies of atoms and molecules are far from satisfactory.[23] For quantitative treatment of multiphoton ionization processes, it is necessary to extend the DFT to properly account for the long-range xc potential such that both the ionization potential and the excited-state properties can be described more accurately. A Krieger–Li–Iafrate (KLI)[24,25] semianalytic treatment of the optimized effective potential (OEP)[26,27] formalism along with the use of an explicit self-interaction-correction (SIC)[22] term has been proposed independently by Chen et al.,[28] but it has been applied to the study of ground-state energies and ionization potentials only. In our previous works,[23] we have extended such a KLI-SIC technique to the time-dependent domain. In this proposed KLI-SIC procedure, similar to the original KLI method, it also allows the construction of a self-interaction-free effective potential that is orbital independent. This avoids the problems associated with the conventional SIC procedure discussed earlier in Ref. [22].
The SIC is very much needed in time-dependent density functional theory (TDDFT) for proper treatment of atomic and molecular time-dependent dynamics such as collisions or MPI processes, etc. The TDDFT is a nontrivial extension of the steady-state DFT of Hohenberg, Kohn, and Sham[8,9] to the time domain. The Runge–Gross (RG) theorem[29] provides the formal foundation of TDDFT. In RG theorem, for any interacting many-particle quantum system subject to a given time-dependent potential, all physical observables are uniquely determined by knowledge of the time-dependent density and the state of the system at any instant in time.[30] The central result of the TDDFT is a set of time-dependent Kohn–Sham equations that are structurally similar to the time-dependent Hartree–Fock (HF) equations but include in principle all the many-body effects through a local time-dependent xc potential. Telnov et al.[31] have presented an alternative nonperturbative formulation of TDDFT based on the extension of the generalized Floquet formalism,[32,33] allowing exact transformation of the time-dependent Kohn–Sham equations into an equivalent time-independent Floquet matrix eigenvalue problem. Such a TDDFT-Floquet formalism provides a time-independent approach for nonperturbative treatment of multiphoton processes of many-electron systems in the presence of intense periodic or multicolor laser fields. Tong et al.[34] have extended this time-dependent approach to the numerical solution of time-dependent Kohn–Sham-like equations in arbitrarily time-dependent fields.
In this paper, we briefly describe several new developments in TDSE and TDDFT for nonperturbative treatment of multiphoton dynamics and nonlinear optical processes of many-electron atoms and molecules in intense laser fields. In Section
Consider an N-electron atom (ion) in an electromagnetic field described by the Coulomb gauge obeys the TDSE, if we neglect relativistic effects and nuclear effects when the atoms interact with strong laser fields, the TDSE can be written in the dipole approximation as (in atomic units)[35]
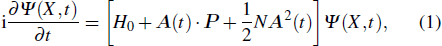

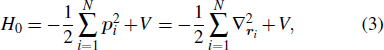

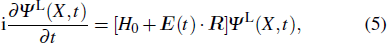

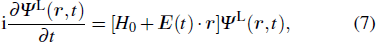
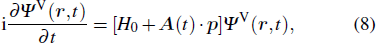
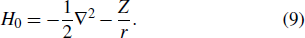
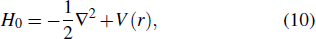
The TDDFT is an extension of the DFT[8,9] to the time domain, providing an alternative approach for nonperturbative treatment of multiphoton processes of many-electron systems in intense laser fields. The central theme of modern TDDFT is a set of time-dependent Kohn–Sham (TDKS) equations which are structurally similar to the TDHF equations but include in principle all the many-body effects through a local time-dependent xc potential. Most applications of TDDFT[37,38] fall in the regime of linear or nonlinear response in weak fields for which the perturbation theory is applicable. In our previous works,[34] we have proposed a TDDFT with optimized effective potential (OEP) and SIC developed for nonperturbative treatment of intense-field atomic multiphoton processes of the atomic and molecular systems. The TDDFT/OEP-SIC formalism takes into account both the electron correlation effect and the structure of the excited states, and at the same time allows for the core excitation of the many-electron systems in intense laser pulses. The method takes into account the dynamic response of all the electronic shells to the external fields and has been applied successfully to the nonperturbative study of MPI and HHG of atoms and diatomic molecules[39,40] in intense laser fields. In the TDDFT/OEP-SIC frame, the TDKS equations of N-electron systems in intense laser fields can be written as
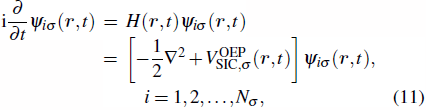
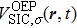

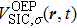

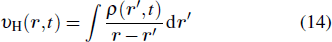
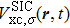
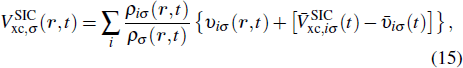
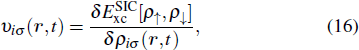
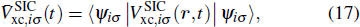
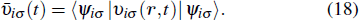
The generalized pseudospectral (GPS) method can be applied to the calculation of multiphoton dynamics and nonlinear optical processes of many-electron atoms and molecules in intense laser fields.[41,42] The essence of the GPS method is to map the semi-infinite domain [0, ∞] or [0, rmax] into the finite domain [–1,1] using a non-linear mapping r = r(x), followed by the Legendre or Chebyshev pseudospectral discretization.[43] This allows for denser grids near the origin, leading to more accurate eigenvalues and eigenfunctions and the use of a considerably smaller number of grid points than those of the equal-spacing grid methods. For example, in Table 

| Table 1. High-precision bound state energies of |
To the time propagation of the wave function, we have extended the GPS method to the time-dependent generalized pseudospectral (TDGPS).[45] The numerical scheme of the TDGPS method consists of two essential steps: (i) The spatial coordinates are optimally discretized in a nonuniform fashion by means of the denser grids near the nuclear origin and sparser grids for larger distances. (ii) A second-order split-operator technique in the energy representation, which allows the explicit elimination of undesirable fast-oscillating high-energy components, is used for the efficient and accurate time propagation of the wave function. To introduce the numerical process of TDGPS in detail, we consider a hydrogen atom case which is convenient due to the similar procedure for many-electron atomic and molecular systems in intense laser fields. The solution of TDSE in Eq. (
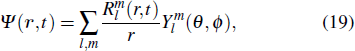
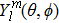
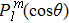
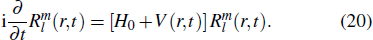
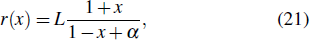
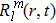

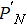
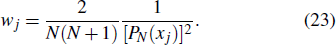

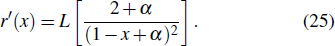
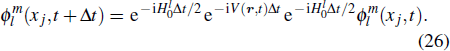

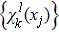
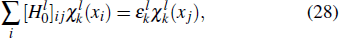
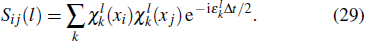
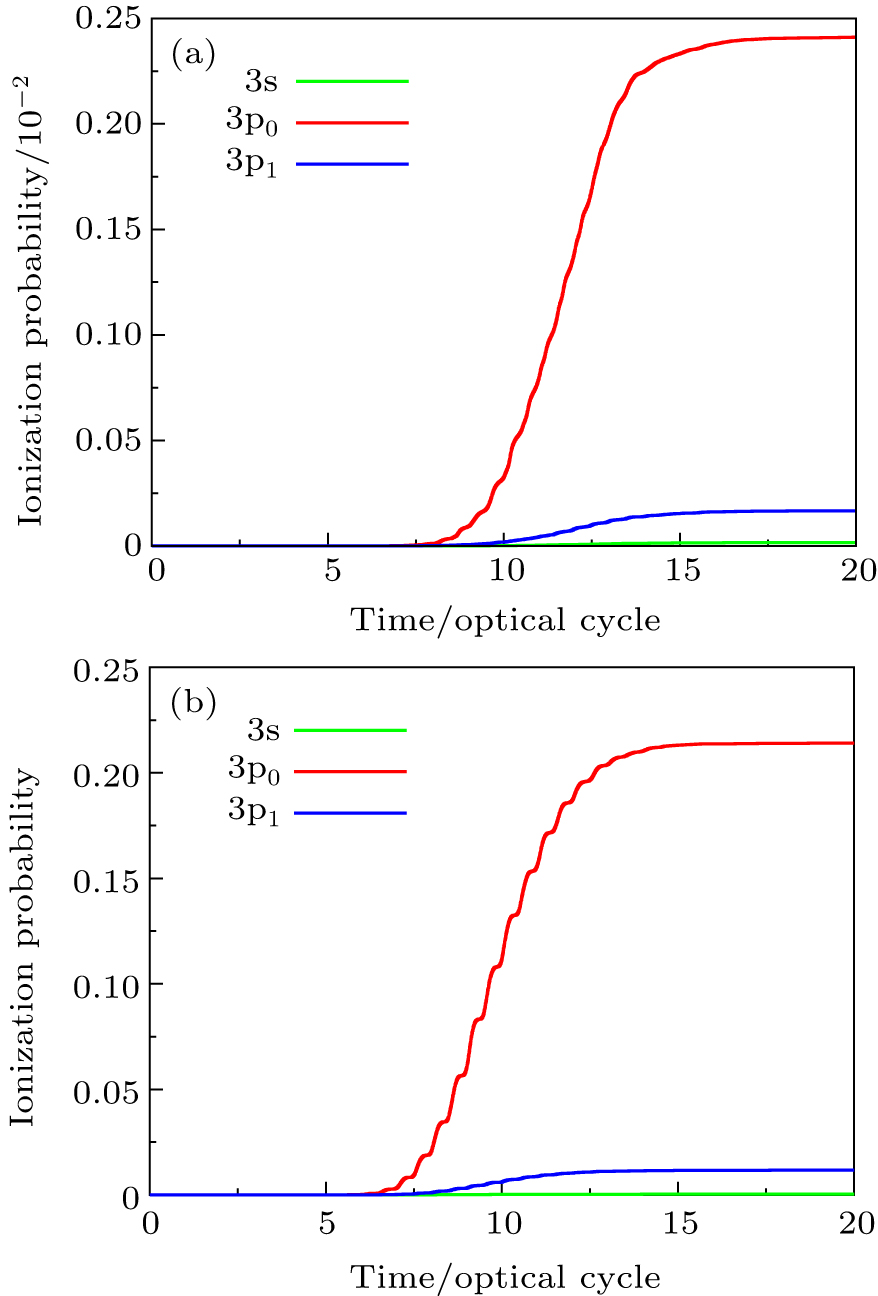
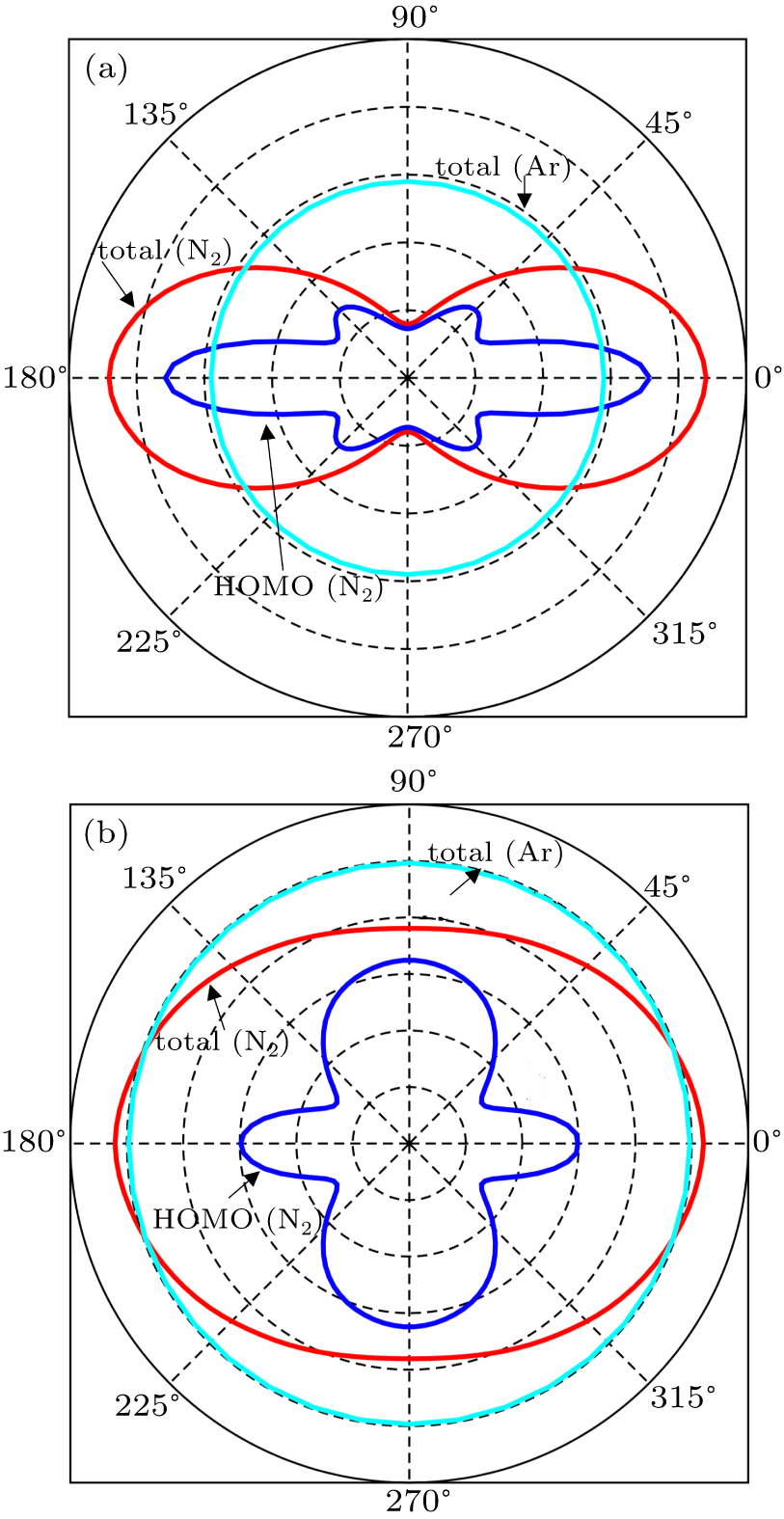
Traditionally many theoretical studies of MPI, ATI, and HHG processes in many-electron atoms and molecules are based on the strong-field approximation (SFA),[3] this approach has its origin in earlier works of Keldysh, Faisal, and Reiss[50–52] as well as in the semiclassical rescattering model.[1,2] While SFA-based models result in rather simple theoretical expressions and produce electron spectra that qualitatively resemble those obtained with accurate numerical wave functions, they fail to give quantitative agreement with more accurate theories. Many attempts have been made recently to improve SFA,[53–55] it has intrinsic restrictions and cannot compete with ab initio calculations for accuracy of the results. On the other hand, SFA-based theories neglect the multielectron dynamics of the target systems. However, the multielectron effects due to the electron exchange and correlation may be significant even when the inner electrons are strongly bound and are not excited by the driving laser field.[56,57] In our previous work,[34,39,40,58] we have extended the TDDFT with proper long-range potential to an all-electron three-dimensional (3D) ab initio study of the MPI of atoms and molecules in intense laser fields, a subject of much current experimental interests.[59–61] Consider a many-electron Ar atom, the time-dependent wave function ψiσ(r,t) in Eq. (

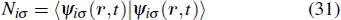
In Fig.
In Figs. 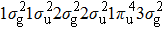
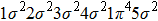
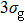
In Figs.
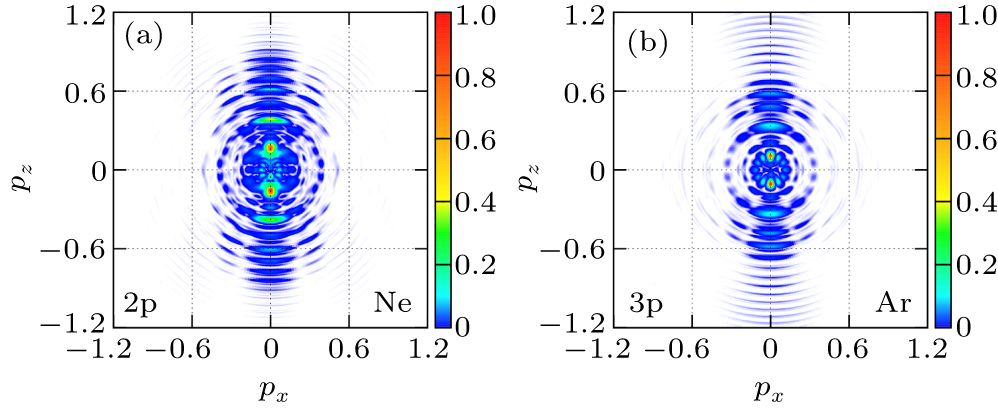
The investigation of above-threshold ionization (ATI)[63] has benefited from the rapid progress of the laser technology. Grasbon et al.[64] have measured ATI photoelectron spectra for noble gas atoms ionized with intense few-cycle laser pulses. Resolutions of the photoelectron momentum distribution in experiments are unprecedentedly high, which has made detailed comparison with theoretical calculations possible. Since the orbital-dependent measurements of the p-state photoelectron momentum distribution are already available,[65] theoretical calculations beyond the SAE approximation are urgently needed.
We have extended the TDDFT/OEP-SIC for the calculation of the photoelectron momentum distribution of the noble gas atoms driven by linearly polarized laser fields. For the ATI calculation, the wave function ψiσ(r,t) is split into inner and outer regions by a smooth masking function, and the photoelectron momentum distribution is found from the outer-region wave function that is propagating in the momentum space with the Volkov Hamiltonian in the velocity gauge.[66–68] We study the photoelectron-momentum-distribution of each individual electron at the end of the time evolution t = tf, given by
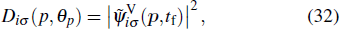
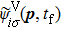
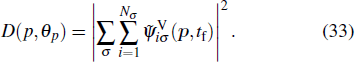
Consider a helium atom, to obtain the accurate calculation of the harmonic spectra of He, an angular-momentum-dependent model potential is constructed in the following form:[69–71]
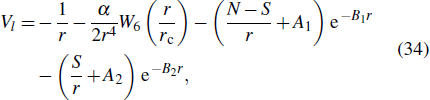

We assume that the laser polarization is along the z-axis. The TDSE in Eq. (
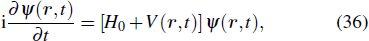
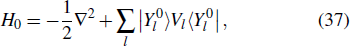
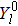
| Table 2. Model potential parameters for He (in a.u.). . |
| Table 3. Comparison of the calculated He atomic energies with the experimental values (in a.u.). For each angular momentum l, two rows of energies En,l are listed: the upper row refers to the calculated model-potential energies, and the lower row refers the experimental values.[NIST] . |
The TDSE is solved accurately and efficiently by means of the TDGPS. Once the time-dependent wave function ψ(r,t) is available, we can calculate the expectation value of the induced dipole moment,
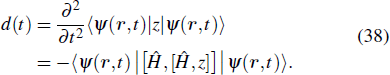
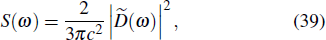
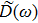
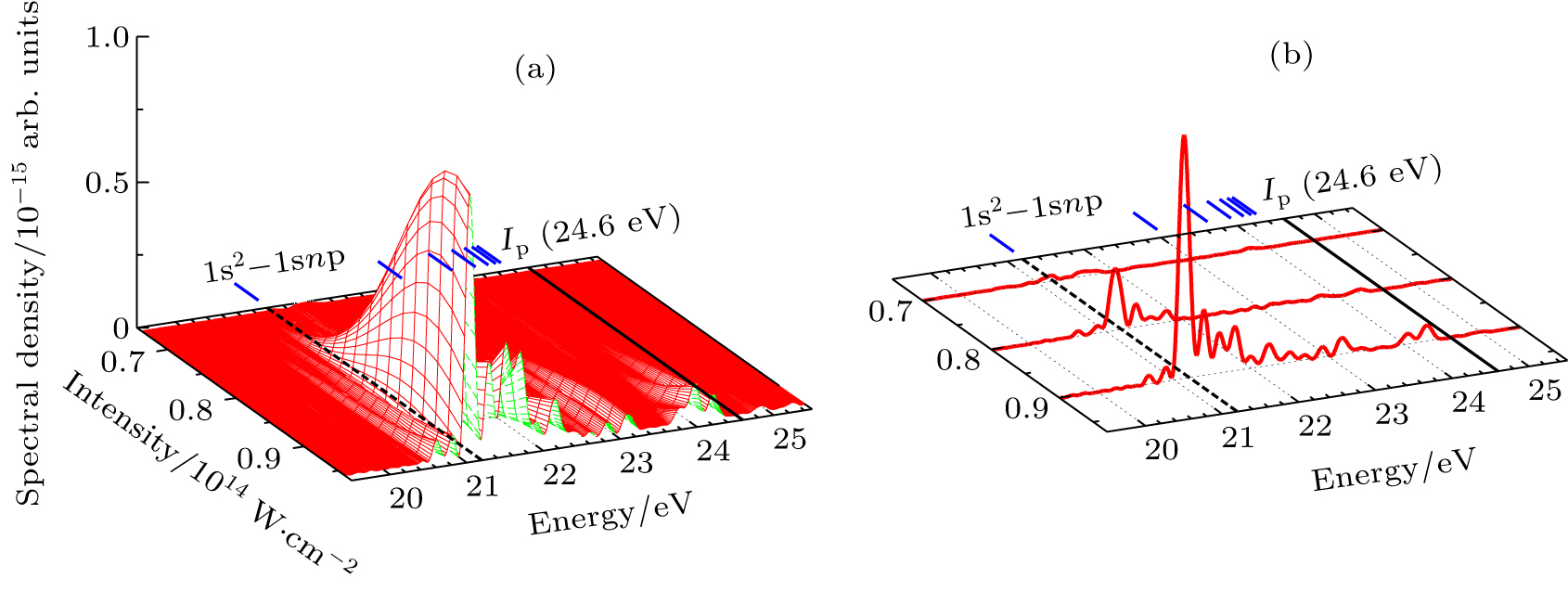
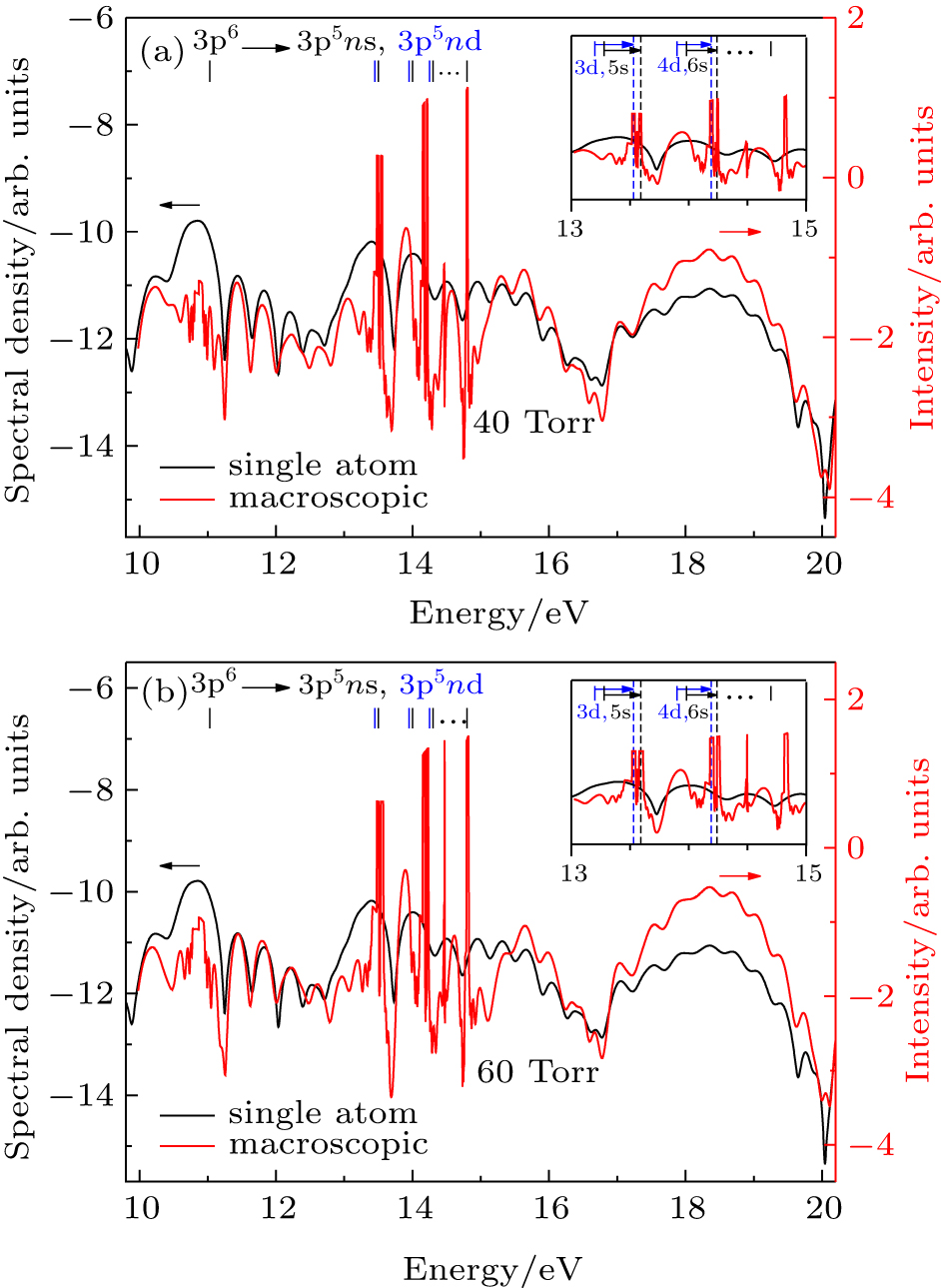
In Figs.
The He atom only has two electrons, all occupying s states, the resonance-enhanced HHG described by the TDSE with an angular-momentum-dependent model potential is sufficient for the single-atom response. For the complex atoms and molecules, the TDDFT can obtain more accurate calculation of the harmonic spectra. In the following, we extend the TDGPS procedure to the numerical solution of the TDKS equations for N-electron atomic systems in intense laser fields. Once the time-dependent wave function ψiσ(r,t) in Eq. (
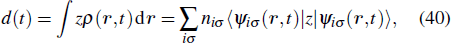
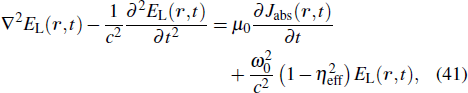
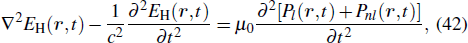
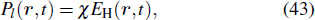
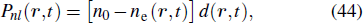
In fact, when the pressure and the laser intensity are low enough, the incident laser field is not modified in the medium, and only the harmonic field has to be propagated. Once equation (

In Fig.
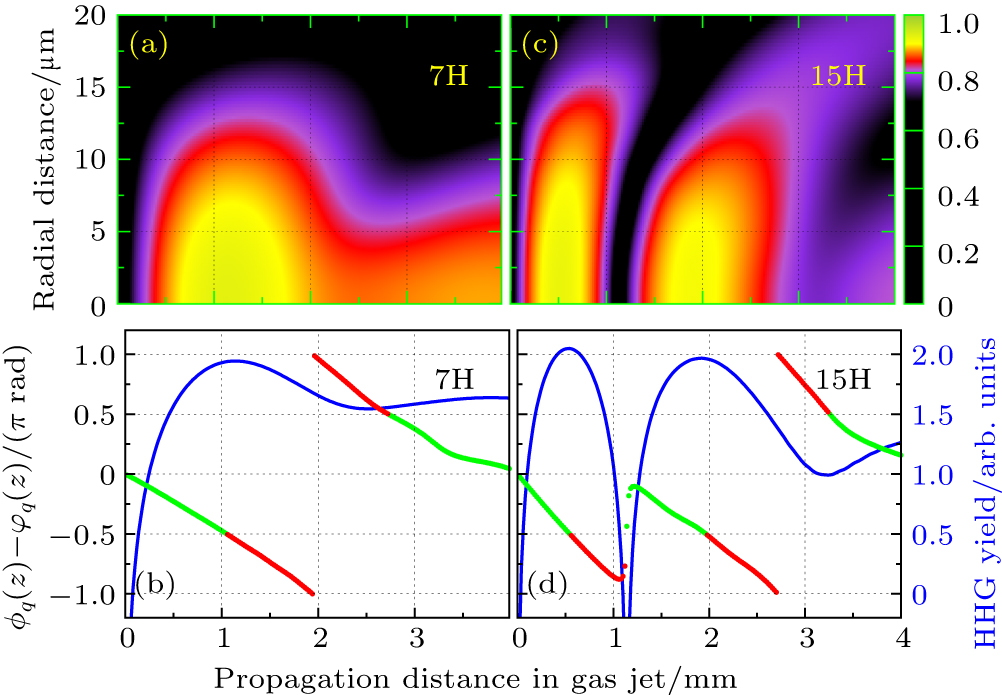
Phase matching plays an essential role in determining the efficiency of macroscopic HHG. The condition for perfect phase-matching (PM) in HHG is obtained when the wavevector of the q-th harmonic kq equals the dipole wavevector kd, which can be written as[81]
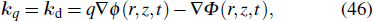
As is well known, such a condition is fulfilled in a Gaussian beam, on-axis and after the focus, when both the phase and intensity decrease along the propagation direction. When the gas medium is placed before the focus, the PM condition is only fulfilled in restricted regions off-axis where the phase and intensity gradients in the radial direction become important. In Figs.
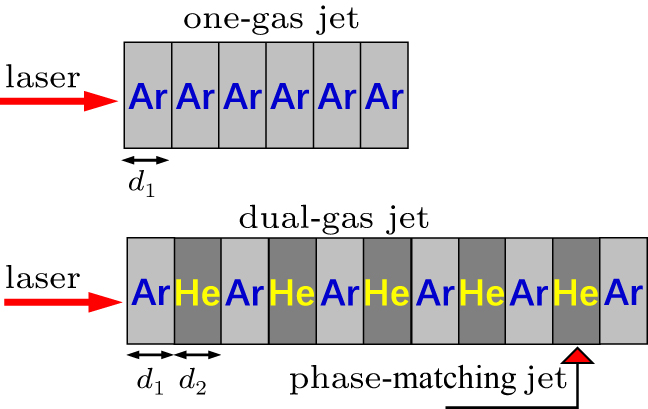
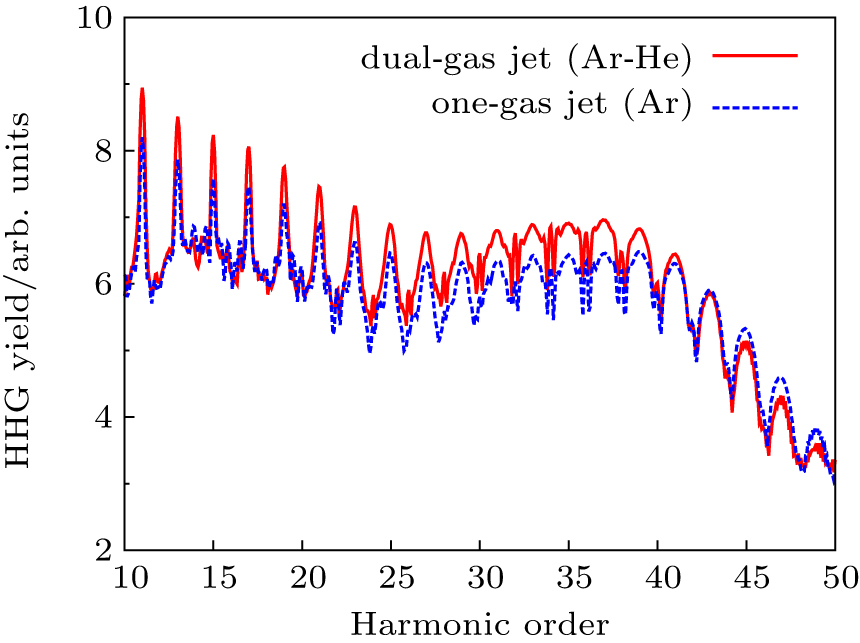
Recently, Willner et al.[84] have developed a novel dual-gas quasiphase matching (QPM) concept based on alternating a HHG generating medium with passive matching hydrogen zones. The choice condition of the dual-gas target proposed by their previous results is that the HHG medium must have a higher ionization potential than the phase matching medium. In Fig.
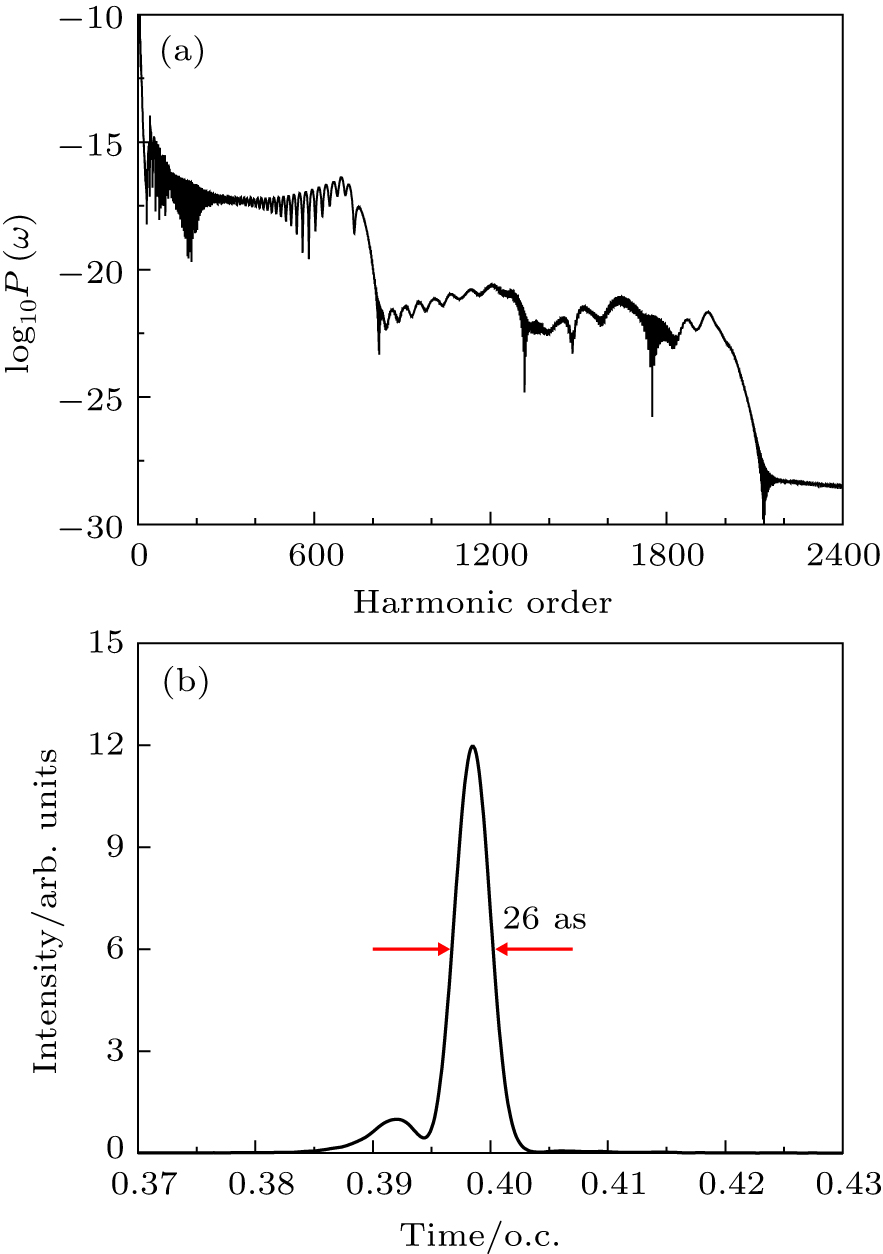
The study of the generation of the APG is a subject of much interest in ultrafast science and technology in the last decade.[85] Currently, the production of the APG by means of the superposition of broadband supercontinuum in HHG is one of the most promising routes. For the generation of the broadband supercontinuum harmonic spectra and ultrashort isolated attosecond pulse, several techniques have been proposed, such as the availability of few-cycle laser pulse,[86,87] double optical gating,[88] multi-cycle driver laser pulses directly from an amplifier,[89] and two- or multi-color laser scheme.[90–99] As an example, consider a helium atoms driven by two color combined laser field, the HHG spectrum can be obtained by the Fourier transformation of time-dependent dipole moment d(t), given by
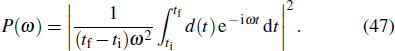
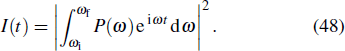
Here, we choose two color combined laser fields in the follow form:
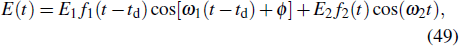
Figure
In summary, we have presented TDSE and TDDFT approaches recently developed for accurate and efficient treatment of the time-dependent dynamics of many-electron atomic and molecular systems. Both the TDSE and TDDFT can be solved by means of the TDGPS methods. The generalized pseudospectral technique allows the construction of non-uniform and optimal spatial grids, denser mesh nearby each nucleus and sparser mesh at longer range, leading to high-precision solution of both electronic structure and time-dependent quantum dynamics with the use of only a modest number of spatial grid points. The TDSE and TDDFT formalism along with the use of the time-dependent GPS numerical technique provides a powerful new nonperturbative time-dependent approach for exploration of the electron correlation and multiple orbital effects on strong field processes. The procedure is demonstrated by several case studies of MPI, ATI, HHG, and APG of atomic and molecular systems, such as He, Ne, and Ar atoms, H2, N2, and CO molecules. The TDDFT is the primary approach available for the treatment of time-dependent processes of many-electron quantum systems in strong fields. Further extension of the self-interaction-free TDDFT approaches to larger molecular systems will be valuable and can lead to significant advancement in the understanding of strong-field chemical physics and atomic and molecular physics in the future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] |