† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant Nos. 2019YFA0307700 and 2017YFA0403300), the National Natural Science Foundation of China (Grant Nos. 11627807, 11774175, 11534004, 11774129, 11975012, and 11604119), the Fundamental Research Funds for the Central Universities of China (Grant No. 30916011207), the Jilin Provincial Research Foundation for Basic Research, China (Grant No. 20170101153JC).
We investigate high-order harmonic generation from atoms irradiated by bichromatic counter-rotating circularly polarized laser pulses by numerically solving the time-dependent Schrödinger equation. It is found that the minimum energy position of the harmonic spectrum and the non-integer order optical radiation are greatly discrepant for different atomic potentials. By analyzing the quantum trajectory of the harmonic emission, discrepancies among the harmonic spectra from different potentials can be attributed to the action of the potential on the ionized electrons. In addition, based on the influence of the driving light intensity on the overall intensity and ellipticity of higher order harmonics, the physical conditions for generating a high-intensity circularly polarized harmonic can be obtained.
With the rapid development of the femtosecond intense laser pulse technology, amplitude of laser electric field has reached the magnitude of the electronic field for an electron acted by the nucleus. When an atom is irradiated by such an intense ultrashort laser pulse, the ultra-wide-band (from ultraviolet to x-ray) coherent high-order harmonic generation (HHG) can be carried out.[1–18] HHG has been applied in the attosecond science[19–21] and nonlinear optics in the XUV region.[22]
The harmonic spectrum from atoms in the linearly polarized laser pulse presents typical characteristics: as the harmonic order increases, the intensity of the first few order harmonics drops rapidly, and then a so-called “plateau” appears, the harmonic intensity which changes little, and there is a cut-off (beyond this energy the harmonic intensity decreases rapidly) at the end of the plateau. The cut-off energy position satisfies the formula Ec = Ip + 3.17Up, Ip is the ionization energy of the atom, and Up is ponderomotive energy. The physical mechanism of HHG can be explained by a three-step model: the bound electron first tunnels through a potential barrier formed by the combined action of a laser electric field and atomic potential, then the ionized electron has the opportunity to return to the parent ion driven by the laser electric field, finally radiate high-energy photons.[23,24]
Usually, linearly polarized driving fields have been considered to produce linearly polarized harmonics. The applications of the linearly polarized harmonic are limited in many aspects, such as x-ray magnetic circular dichroism,[25] discrete molecular symmetry,[26–30] spin dynamics,[31–34] and recognizing chirality in molecules via photoelectron circular dichroism at their intrinsic timescales.[35–37] Due to the larger frequency range of the harmonic spectrum, it is difficult to directly convert the harmonic polarization from the linear polarization to the circular one. Therefore, some schemes are proposed to generate the circularly polarized harmonic by shaping the driving pulse or controlling the atomic target. For generating circularly polarized harmonic, Yuan et al. adopted molecules interacting with the circularly polarized laser pulses with multiple frequencies.[38] Kfir et al. found experimentally that the circularly polarized harmonic can be obtained from atoms irradiated by counter-rotating two-color (with frequencies of ω and 2ω) circularly polarized (CRTCCP) laser fields.[39] This method was suggested firstly by Becker et al.,[40,41] and investigated deeply in experiments and theories.[25,39,42–45] When the atom is irradiated by the CRTCCP laser pulse, the polarization of the 3n + 1 and 3n + 2 order harmonics are the same as those of the fundamental and double frequencies, respectively. Furthermore, the 3n order harmonics in the HHG spectra are suppressed.[39,46] The effect of the laser wavelength on the harmonic efficiency was discussed.[47–50]
In order to achieve a higher HHG yield, a higher gas density is required. Due to the ionization of the atom irradiated by the driving laser pulse, the system is in the plasma state. The atomic potential is influenced by the ionized electron, and sometime the potential felt by the electron is described by the short-range Debye–Hückel model.[51] The short-range potential model is also used to understand the role of the excited states on the generation of high harmonic. Faria et al. demonstrated the resonance effect of the potential function on atomic harmonics.[52] Li et al. compared the harmonic and ionization characteristics of lithium atoms with short-range and long-range model potentials.[53] Liu et al. analyzed the role of potential functions on the generation of attosecond pulses.[54] In order to optimize the generation of high-order harmonic of an atom driven by a CRTCCP laser pulse, we investigate the potential function role on the process of HHG. The structure of the paper is as follows: In Section
Under the dipole approximation and the length gauge, the response of an atom irradiated by the strong laser field can be described by the time-dependent Schrödinger equation:


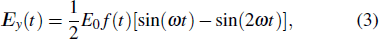



The corresponding harmonic radiation spectrum is obtained by


In order to understand the harmonic generation mechanism, the time-frequency behavior is calculated from the wavelet transform of the dipole moment




The potential functions used in this paper are the long-range softened Coulomb potential 

 | Fig. 1. Harmonic emission spectra of long-range (a) and short-range (b) atoms in the CRTCCP laser pulse. |
In order to further understand the effect of the potential function on the harmonic intensity, we systematically investigate the intensity variation of the harmonic generated from the long-range model (Fig.
 | Fig. 2. The variation of harmonic spectra with the peak amplitude of the laser electric field calculated from the long-range model atom (a) and the short-range model atom (b). |
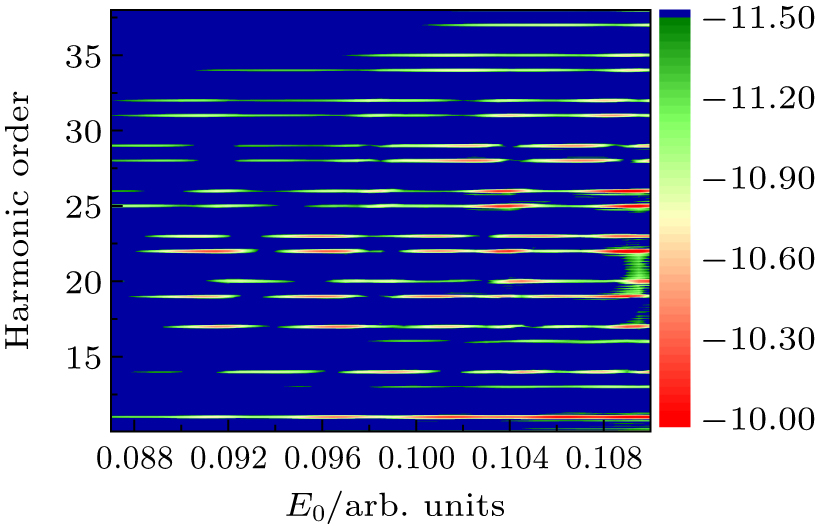 | Fig. 3. The variation of harmonic spectra with the peak amplitude of the laser electric field calculated from the SFA. |
The intuitive distinction of the harmonic spectra from the three cases is the non-integer order harmonic emission, as presented in Figs.
The other difference among these calculations is the suppression of 3n + 1 and 3n + 2 order harmonics. For example, the 26th harmonic intensity from the short-range atom is obviously suppressed (white box in Fig.
For understanding the physical mechanism of the suppression of 3n + 1 and 3n + 2 order harmonics, we study the transient process of harmonic quantum emission. The quantum trajectories of harmonic emission are obtained by wavelet transform. The path with the earlier ionization time and the later emission time is called the long trajectory, and the path with the later ionization time and the earlier emission time is called the short trajectory. The positive and negative slope branches in the red box in Fig.
Figure
In the following, we systematically analyze the change of the HHG yield with the driving laser intensity. The harmonic yield can be defined as the energy integral in a fixed photon energy range.[58] In this work, the harmonic yield is integrated from 31 eV to 62 eV: 

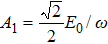

From the above analysis, it is found that the harmonic intensity is affected by the potential function of the atom. In order to obtain a circularly polarized harmonic with high intensity, it is necessary to analyze the ellipticity of the harmonic emission. The ellipticity of the harmonic can be obtained by ε = [(|D+|) − (|D−|)] /[(|D+|) + (|D−|)],[61] where 
In summary, we have theoretically studied the effect of the potential function on the harmonic emission of atoms driven by a bichromatic counter-rotating circularly polarized laser field. It is found that different potential functions result in an obvious distinction in the intensity minimum position of the harmonic spectra and the generation of the non-integer order harmonic emission. Through the analysis of quantum trajectories in one optical period, the intensity minimum in the harmonic spectra can attribute to the interference between different quantum trajectories. In addition, the variation of the harmonic ellipticity with the driving laser intensity is also discussed. Due to the sensitivity of the harmonic intensity and polarization on the potential function, one can generate the circularly polarized harmonic radiation with high intensity by optimizing atomic and molecular targets.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] |




